近景摄影测量提高裸露地表粗糙度测量精度

陶浩然，陈 权，李 震，曾江源，陈晓宁

近景摄影测量提高裸露地表粗糙度测量精度

陶浩然1,2，陈 权2※，李 震2，曾江源2，陈晓宁1

（1. 西安科技大学测绘科学与技术学院，西安 710054；2. 中国科学院遥感与数字地球研究所航空遥感中心，北京 100094）

微波遥感观测量对地表参数敏感，可用于对土壤水分、地表粗糙度和植被信息的定量提取。地表粗糙度参数实测值，是遥感反演结果验证、精度评价，以及各类遥感反演算法中的重要参量，但一直缺少一种简便、快捷、高精度的获取手段。该研究将近景摄影测量方法和微波遥感领域传统地表粗糙度测量的针板法进行对比，分析2种方法均方根高度及相关长度的测量结果，表明近景摄影测量法可以有效提高粗糙度实地测量精度；以近景摄影测量法全角度粗糙度参数的均值作为实测真实值，表明传统针板法测量的均方根高度误差达到12%～35.1%，相关长度误差最大能达到19.6%～62.4%；分析了采样间隔和采样数目对粗糙度测量的影响，表明针板法采用1 cm的间隔是实际地表较好的选择，但仅采用2个方向均值的测量方法必然带来很大误差，同时得出测量次数大于12时，测量结果趋于稳定并可认定为真值的结论；此外，研究表明，在一些传统针板法无法提取粗糙度的情况，近景摄影测量法依然有效。该研究表明，近景摄影测量法的非接触式、高精度、采样间隔及采样频率可调节等特征，为微波遥感工作提供了有效的地表粗糙度地面实测手段。

遥感；粗糙度；测量；近景摄影测量；点云；采样间隔

陶浩然，陈 权，李 震，曾江源，陈晓宁. 近景摄影测量提高裸露地表粗糙度测量精度[J]. 农业工程学报，2017，33(15)：162－167. doi：10.11975/j.issn.1002-6819.2017.15.021 http://www.tcsae.org

Tao Haoran, Chen Quan, Li Zhen, Zeng Jiangyuan, Chen Xiaoning. Improvement of soil surface roughness measurement accuracy by close-range photogrammetry[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(15): 162－167. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.15.021 http://www.tcsae.org

0 引 言

土壤表面粗糙度定义为一定区域内土壤表面的不规则度，受土壤质地、粒径、岩屑及植被覆盖等因素的综合影响[1]。土壤粗糙度影响地表含水量、地表入渗、地表径流并最终影响泥沙的搬运与沉积[2]。地表粗糙度不仅可以表征土壤表面的起伏程度，亦对地表与雷达入射波之间的相互作用产生重要影响，是微波对地观测参数反演领域的研究重点，还是Oh等[3-5]等地表微波散射模型的重要输入参数之一，很大程度上决定了后向散射回波强度[6]，是影响土壤水分反演精度的一个至关重要的地表参数[7]，其对后向散射系数的影响有时甚至会超过土壤水分[8]。为了建立准确的地表前向电磁散射模型和遥感反演模型，在观测试验中同步进行的土壤粗糙度的采集是最常用的方法[9]，目的是利用实测数据校正粗糙度对后向散射系数的影响。

根据测量方式的差异将地表粗糙度测量方法分为接触式和非接触式2种。常用的接触式测量主要包括链条法及针板法等。链条法因只能计算单一参数，无法获取剖面形状，具有较大的局限性[10]。而常用的非接触式测量方式主要包括：超声波测量法[11]、激光扫描法[12-14]、摄影测量法[15]等。超声波测量易产生声波的多次反射而造成精度降低；三维激光扫描法设站次数较少时易产生测量漏洞，设站次数较多则会涉及数据拼接问题并大幅增加作业时间，且测量仪器价格昂贵。针板法是目前微波遥感研究及实际应用中广泛采用的测量方法[16]，但每次测量仅取2个垂直方向的平均值代表整个区域的粗糙度值，精度较低。近年来，随着数码相机的普及以及影像匹配算法的发展，使得利用摄影测量进行地表粗糙度测量成为可能。近景摄影测量法不需要携带针板等体积较大的实验仪器，在野外考察工作中有很强的实用性；也可避免针板法测量次数较少等问题造成的测量误差，有效提高地表粗糙度测量精度，改善后续如地表参数反演等工作的精度，这是针板法测量地表粗糙度所不具备的优势。本研究通过对比针板法和近景摄影测量法在地表粗糙度测量中的实际情况，证明近景摄影测量法可以有效提高地表粗糙度测量的效率及精度。

1 粗糙度相关参数

在微波遥感领域，地表粗糙度一般用2个主要参数进行表征，分别是均方根高度σ和表面相关长度l，它们分别从垂直与水平2个方向上对地表粗糙度状况进行刻画[17]。

1.1 均方根高度σ

假设平面x-y内一点(x,y)的高度为z(x,y)，在表面上取统计意义上有代表性的一块，尺度分别为Lx和Ly，并将原点置于平面中心，则该表面平均高度为：

该变量平方的数学期望为：

则定义均方根高度σ为：

对于离散数据，均方根高度σ为：

1.2 表面相关长度l

定义表面在x方向的高度为z(x)，则表面的归一化自相关函数为：

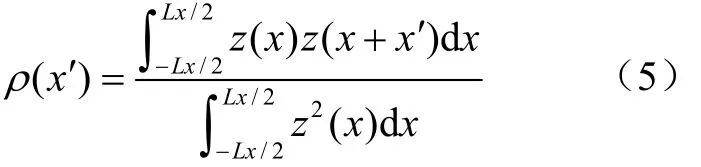
它是x点的高度z(x)与x相距x′另一点的高度z(x+x′)之间相似性的一种度量，对于离散数据，相距x′=(j−1)x的归一化自相关函数由下式给出：

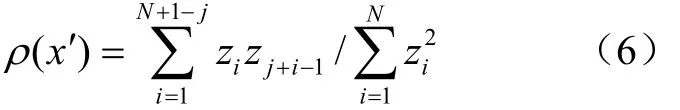
式中j为自然数。

表面相关长度l是估计表面上两点相互独立的一种标准，即如果两点在水平距离上相隔距离大于l，那么该两点的高度值，从统计意义上说是近似独立的。

2 数据与方法

2.1 传统针板法

目前常采用的地表粗糙度测量方法主要是针板法，针板法利用的主要工具是针板，针板由一排等长、等距排列的探针及增加对比度所用的黑板等部件组成，如图1所示。测量时探针与待测地表接触，用相机记录探针针尾的起伏状态后在电脑上进行数字化并转换图像坐标，得到测针所表示的各点高程值，从而计算出地表粗糙度。

针板造价低廉，操作简单，被微波遥感领域的研究人员广泛使用。然而针板法测量粗糙度属于接触式测量，操作时探针与地表接触，不可避免地对地表结构造成一定的破坏，特别是对于疏松地表地形的破坏更是不可忽略[18-20]，同时还会造成探针末端插入地表，增大测量误差。因地表粗糙度的均方根高度和表面相关长度与采样间隔有关，测针之间较大的间隔易造成地表粗糙度的低估，且其对于表面相关长度l的影响要大于均方根高度σ[21]。另外，在野外实测过程中，常取某一方向及与之垂直方向的2组粗糙度参数并求平均从而得到该地地表粗糙度值，因测量次数较少，使得测量的粗糙度参数值带有较大的偶然性[22]，精度较低。

图1 传统针板法测量地表粗糙度Fig.1 Measurement of soil roughness by traditional pin-profiler method

2.2 近景摄影测量法

近景摄影测量法采用非量测相机获取多基线待测区域影像，利用空中三角测量光束法获取影像的外方位元素并对影像进行密集匹配来生成目标区域三维点云，再对密集点云进行处理获取地表粗糙度，如图2所示。

实际测量过程借鉴航空摄影测量方法，对待测地表进行多航带立体像对获取。影像的分辨率决定了三维重建的细节质量，与点云相关的影像数量直接决定了投影的几何精度。因此在进行摄影测量微地表重建的过程中，使用非量测相机以较高的像片重叠数（＞10）及较高的图像分辨率来获取高精度的粗糙度测量结果（本试验地面分辨率为0.462 mm/pix，重投影均方根误差为0.178 mm），同时进行多角度拍摄，防止出现像片漏洞而导致的点云不连贯。同时，需要在试验区域内放置如图3所示的金属定标板并保证定标板水平（定标板上印有6个编码元作为控制点），用以确定像片中每个像素代表的地面实际长度值。

本文利用Agisoft Photoscan软件进行点云的重建工作，软件利用优化的SIFT算法[23]进行密集点的匹配。该算法首先建立高斯差分（DoG）尺度空间，并在尺度空间内检测极值点；然后利用关键点邻域像素的梯度方向分布特性为每个关键点指定方向参数，使算子具备旋转不变性；再生成关键点描述子并完成关键点的匹配，最后利用RANSAC（random sample consensus，随机抽样一致）消除错配点，其具有良好的鲁棒性。该软件通过光束法平差(bundle adjustment)确定内外方位元素[24]，并通过多视角立体视觉算法进行三维点云重建。最后对生成的点云进行量测，达到非接触式测量的效果。

近景摄影测量的误差来源主要有：相机的分辨率及性能，所摄相片数量，摄影距离等[25]。因此仪器硬件性能方面应保证相机具有较高的分辨率（大于500万像素），镜头应利用焦距为20～80 mm（35 mm等效焦距）的定焦镜头或变焦镜头的远近两端（拥有较为稳定的机械结构）。使用时应设定较高的快门速度和较低的ISO感光度，避免图像模糊或引入噪点而增大测量误差。

图2 近景摄影测量法测量地表粗糙度Fig.2 Measurement of soil surface roughness by close-range photogrammetry method

图3 近景摄影测量法定标板示意图Fig.3 Schematic diagram of calibration board of close-range photogrammetry

近景摄影测量法估测地表粗糙度方法主要的优点是仅利用普通的非量测型相机，便可获取待测区域地表高精度点云数据，获取数据方式为面状，相较于针板法的线状粗糙度获取数据量大大增加，使粗糙度测量的偶然误差有效降低，且精度可以大幅度提高。

2.3 数据获取

试验中选用的针板全长95 cm，测针共92根且每根测针相距1 cm（即采样间隔为1 cm）。选择北京航天城附近一块面积较大的裸土地块作为在试验区域，并在该区域选择某一方向利用针板测量粗糙度，并用相机记录，在与之垂直方向再次测量粗糙度，求取均值作为该地块粗糙度参数。同时，为了比较不同粗糙度情况下的效果，本试验对粗糙度不同的3块区域分别进行了测量。

在相同试验区域利用近景摄影测量法进行试验，利用获取的高重叠度影像生成地表密集点云，选取以针板测量区域中心为圆心，92 cm为直径的圆内的点云，截取的圆形点云如图4所示。在内业计算中，通过设定一定的采样间隔及采样范围大小，并任意旋转采样线，可以获得试验区域内任意角度、任意采样间隔的地表粗糙度参数值。

图4 截取圆形点云示意图Fig.4 Schematic diagram of circular point cloud

3 结果与分析

3.1 采样角度与地表的各向异性

有研究表明，作物区土壤地表具有较强的空间异质性，相同区块土壤均方根高度和相关长度最大变异系数分别可达25.4%和94.5%[26]。地表粗糙度测量结果的准确性将直接影响微波反演地表参数的结果，而地表的各向异性正是造成测量误差的原因之一。

从图5和图6中粗糙度参数随角度变化关系可以看出：均方根高度和相关长度都会随采样角度产生较大变化，且变化趋势较平滑，符合实际地表连续变化的特征。测量地表粗糙度应利用近景摄影测量法综合多角度进行测量，增加测量角度，增大测量范围，将线采样模式扩展为面采样，减少针板法因测量方向不足而带来的偶然误差，准确获取土壤表面粗糙度的各向异性特征，并解决空间异质性造成的测量误差问题。

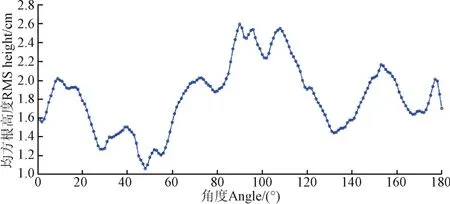
图5 均方根高度随采样角度变化规律Fig.5 RMS height varies with sampling angle

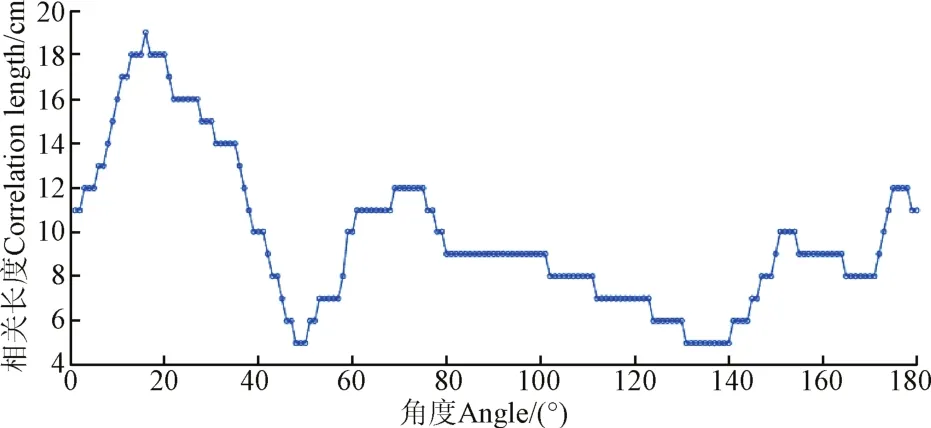
图6 相关长度随采样角度变化规律Fig.6 Correlation length varies with sampling angle

3.2 采样数目与采样间隔

通常，采样长度越长，测得的地表粗糙度值越准确[27-28]。有研究表明，为使均方根高度及表面相关长度与真值的误差小于10%，采样长度应是均方根高度及表面相关长度的40倍和200倍[29]。然而在实际测量过程中，将采样长度扩大到表面相关长度的200倍是行不通的，传统针板法长度的限制使得测量值与真值之间存在较大的误差。在近景摄影测量方法中，可以在内业计算中增加采样次数来弥补采样长度不足造成的误差[22]。

图7表示了2种地表粗糙度参数统计量随采样数的变化规律，可以看出均方根高度及相关长度随着采样数的增加逐渐趋于固定值，即随着采样间隔的减小均方根高度及相关长度的测量误差逐渐减小，最后趋于稳定。从图7可以看出当采样数目大于12时，可认为测量结果稳定为真值。

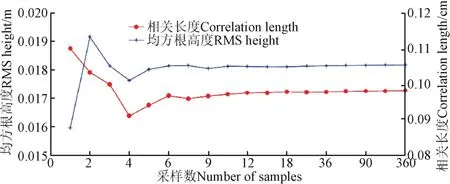
图7 均方根高度及表面相关长度随采样数目变化图Fig.7 RMS height and correlation length varies with number of samples

表1给出了采样的剖面随采样间隔的变化情况。由表1可见，在采样间距小于1 cm时，所截得的剖面较为一致，与之对应的均方根高度和相关长度趋于稳定。故此认为地表微地形起伏具有一定的固有频率，根据Nyquist采样定理[30]，当采样频率大于Nyquist采样频率，可通过采样点重建地表粗糙度剖面；采样率不足即采样间隔过大时，不满足采样定理而无法重建地表粗糙度；而适当进行过采样可以较好地重建出地表粗糙度，并能增强粗糙度参数测量的稳定性。由表1的统计结果，我们认为当采样间隔小于等于1 cm时可以精确刻画出地表粗糙度剖面并准确计算粗糙度参数，这也是传统针板法常采用1 cm间隔的原因。

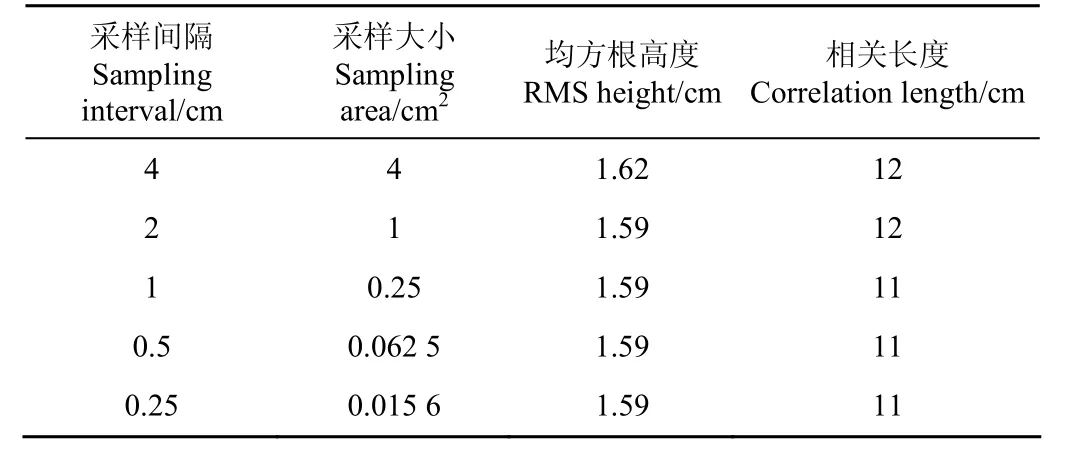
表1 近景摄影测量法地表粗糙度参数随采样间隔变化统计表Table 1 Statistical table of soil surface roughness parameters changing with sampling interval by close-range photogrammetry

3.3 2种测量方式对比结果

试验分别在粗糙度不同的3块试验区进行，表2为分别在3个试验区域进行的2种粗糙度测量方法对比试验的统计结果。其中，摄影测量法的均方根高度及相关长度测量结果（表中“平均值”）是圆形点云上各方向测量值平均，角度间隔均为1°；针板法测量的地表粗糙度统计值的平均值为相互垂直2次测量结果的平均值。通过以上对近景摄影测量法测量原理的分析，近景摄影测量法非接触的测量方式不会对地表结构造成破坏，且12次采样后结果稳定，所以，取摄影测量法全角度360次测量值的均值作为真值。从上表的统计结果可以看出：除了采样次数不足产生的误差外，传统针板法测量的均方根高度值较摄影测量法偏小，原因为接触式测量破坏了部分地表微结构[31]，测针对疏松土质及潮湿地表的垂直方向产生压力，使地表趋于平滑，导致均方根高度低于真值，并在一定程度上破坏了土壤表面的自相关性，

使得针板法相关长度测量值较真值偏低。

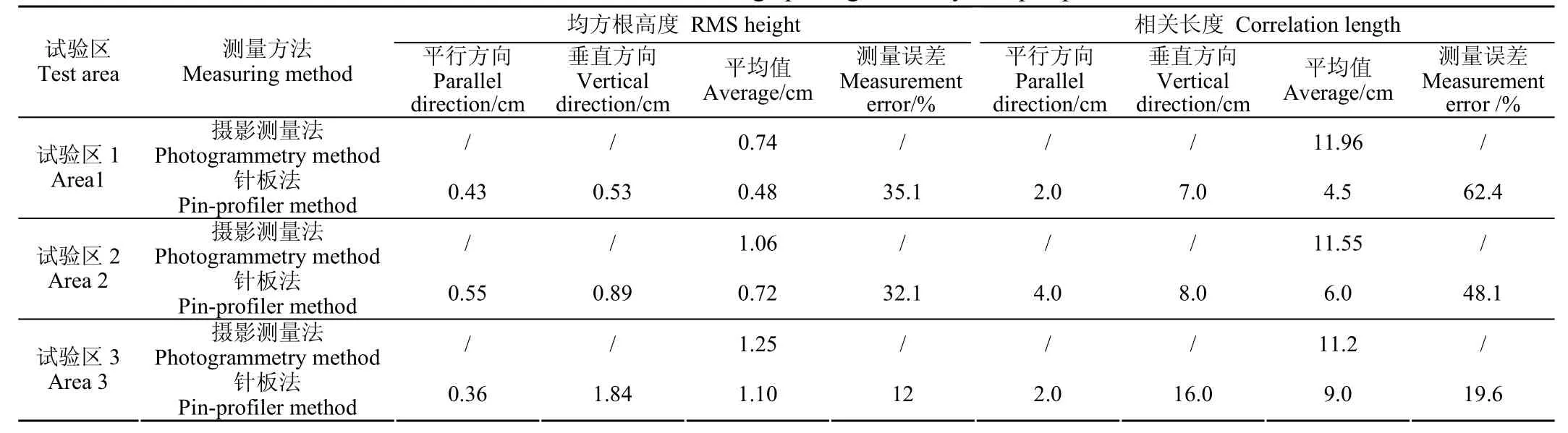
表2 近景摄影测量法与针板法测量结果统计表Table 2 Statistical table of close-range photogrammetry and pin-profiler method

3.4 极端地表应用情况

地表自相关函数（autocorrelation function）能有效度量x点的高度z(x)与x相距x′另一点的高度z(x+x′)之间的相似性，由自相关函数计算出的表面相关长度则能有效刻画水平方向上的相互独立的程度。

根据表面相关长度的定义，在图8所示的某些极端地表，可能会出现因针板法自身的不稳定性及破坏地表微结构而使测量的相关长度过小，出现Oh模型[3]等散射模型不适用的情况，如Oh模型相关长度的适用范围为2.5～20 cm。图8中，针板法与摄影测量法的相关长度分别为2和4，针板法测量结果并不合理，摄影测量法则能避免这一情况的发生，在某些极端地表时更为有效。

图8 极端地表针板法与近景摄影测量法自相关函数对比图Fig.8 Comparison of auto correlation function between close-range photogrammetry and pin profiler method in extreme soil surface

4 结 论

近景摄影测量法利用摄影测量原理获取待测区域地表影像，密集匹配后生成待测地表高精度点云，并在生成的密集点云上进行量测。与传统针板法相比，具有如下优点：

1）提高精度及效率。从本文的试验中可见，针板法测量地表均方根高度误差范围12%～35.1%，而相关长度测量误差达到19.6%～62.4%，近景摄影测量法可便利地调整采样角度，准确刻画地表粗糙度的各向异性；并能大幅增加采样数目，解决地表空间异质性造成的测量误差问题，本文同时指出当采样次数大于12次时，测量结果趋于稳定，可作为测量真值。

2）解决有些地表无法测量的问题。非接触式的近景摄影测量法避免了测量过程对地表微结构的破坏，解决了部分极端地表针板法测量导致粗糙度参数超出地表电磁散射模型适用范围的问题。

3）定义近景摄影测量法的采样间隔问题。采样间隔及数目的设置应满足Nyquist采样定理，适当进行过采样能较好地重建出地表剖面，避免采样间隔过大或过小导致的采样不足和增加野外工作量。

目前在微波遥感研究中使用的地表粗糙度参数都是基于水平或垂直2个方向上的二维参数，而在雷达对地观测过程中，不同波长的雷达波以不同方向及入射角照射地面，得到的后向散射系数有显著差异，仅从水平与垂直2方向刻画土壤粗糙度并不能精确地反映其散射机理。利用摄影测量法测得的三维表面则可以从各角度获取粗糙度值，对深入研究微波散射的物理机制，将近景摄影测量方法得到的地表粗糙度测量值引入到地表散射正向模型以及地表参数反演模型，是下一步研究的重点。

[1] Thomsen L M, Baartman J E M, Barneveld R J, et al. Soil surface roughness: Comparing old and new measuring methods and application in a soil erosion model[J]. Soil, 2015, 1(1): 399－410.

[2] Amoah J K O, Amatya D M, Nnaji S. Quantifying watershed surface depression storage: Determination and application in a hydrologic model[J]. Hydrological Processes, 2013, 27(17): 2401－2413.

[3] Oh Y, Sarabandi K, Ulaby F T. An empirical-model and an inversion technique for radar scattering from bare soil surfaces[J]. Ieee Transactions on Geoscience and Remote Sensing, 1992, 30(2): 370－381.

[4] Dubois P C, Van Zyl J, Engman T. Measuring soil moisture with imaging radars[J]. IEEE Transactions on Geoscience & Remote Sensing, 1995, 33(4): 915－926.

[5] Fung A K, Li Z, Chen K S. Backscattering from a randomly rough dielectric surface[J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(2): 356－369.

[6] Barber M E, Grings F M, Alvarez-Mozos J, et al. Effects of spatial sampling interval on roughness parameters and microwave backscatter over agricultural soil surfaces[J]. Remote Sensing, 2016, 8(6): 458.

[7] Altese E, Bolognani O, Mancini M, et al. Retrieving soil moisture over bare soil from ERS 1 synthetic aperture radar data: Sensitivity analysis based on a theoretical surface scattering model and field data[J]. Water Resources Research, 1996, 32(3): 653－661.

[8] Bourgeau-Chavez L L, Kasischke E S, Riordan K, et al. Remote monitoring of spatial and temporal surface soil moisture in fire disturbed boreal forest ecosystems with ERS SAR imagery[J]. International Journal of Remote Sensing, 2007, 28(10): 2133－2162.

[9] 李俐，王荻，王鹏新，等. 合成孔径雷达土壤水分反演研究进展[J]. 资源科学，2015，37(10)：1929－1940.

Li Li, Wang Di, Wang Pengxin, et al. Progress on monitoring soil moisture using SAR data[J]. Resources Science, 2015, 37(10): 1929－1940. (in Chinese with English abstract)

[10] 朱良君，张光辉. 地表微地形测量及定量化方法研究综述[J].中国水土保持科学，2013，11(5)：114－122.

Zhu Liangjun, Zhang Guanghui. Review of measurement and quantification of surface microtopography[J]. Science of Soil and Water Conservation, 2013, 11(5): 114－122. (in Chinese with English abstract)

[11] Robichaud P R, Molnau M. Measuring soil roughness changes with an ultrasonic profiler[J]. Transactions of the Asae, 1990, 33(6): 1851－1858.

[12] 李晓洁，赵凯，郑兴明. 基于激光三角法的地表粗糙度测试仪的研制[J]. 农业工程学报，2012，28(8)：116－121.

Li Xiaojie, Zhao Kai, Zheng Xingming. Development of surface roughness tester based on laser triangulation method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(8): 116－121. (in Chinese with English abstract)

[13] Martinez-Agirre A, Alvarez-Mozos J, Gimenez R. Evaluation of surface roughness parameters in agricultural soils with different tillage conditions using a laser profile meter[J]. Soil & Tillage Research, 2016, 161: 19－30.

[14] Milenkovic M, Pfeifer N, Glira P. Applying terrestrial laser scanning for soil surface roughness assessment[J]. Remote Sensing, 2015, 7(2): 2007－2045.

[15] Welch R, Jordan T R, Thomas A W. A photogrammetric technique for measuring soil-erosion[J]. Journal of Soil and Water Conservation, 1984, 39(3): 191－194.

[16] Stenberg L, Tuukkanen T, Finer L, et al. Evaluation of erosion and surface roughness in peatland forest ditches using pin meter measurements and terrestrial laser scanning[J]. Earth Surface Processes and Landforms, 2016, 41(10): 1299－1311.

[17] 刘伟. 植被覆盖地表极化雷达土壤水分反演与应用研究[D].北京：中国科学院遥感应用研究所, 2005. Liu Wei. Study on Soil Moisture Inversion and Application With Polarization Radar in Vegetated Area[D]. Beijing: Institute of Remote Sensing Applications Chinese Academy of Sciences, 2005. (in Chinese with English abstract)

[18] Jester W, Klik A. Soil surface roughness measurement & mdash; methods, applicability, and surface representation[J]. Catena, 2005, 64: 174－192.

[19] 江冲亚，方红亮，魏珊珊. 地表粗糙度参数化研究综述[J].地球科学进展，2012，27(3)：292－303.

Jiang Chongya, Fang Hongliang, Wei Shanshan. Review of land surface roughness parameterization study[J]. Advances in Earth Sciences, 2012, 27(3): 292－303. (in Chinese with English abstract)

[20] Podmore T H, Huggins L F. An automated profile meter for surface-roughness measurements[J]. Transactions of the Asae, 1981, 24(3): 663－665.

[21] Oh Y, Hong J Y. Effect of surface profile length on the backscattering coefficients of bare surfaces[J]. Ieee Transactions on Geoscience and Remote Sensing, 2007, 45(3): 632－638.

[22] 郑兴明，赵凯，李晓洁. 农田表面粗糙度参数的测量与精度分析[J]. 地球信息科学学报，2013，15(5)：752－760.

Zheng Xingming, Zhao Kai, Li Xiaojie. Accuracy analysis of agriculture soil surface roughness parameter[J]. Journal of Geo-Information Science, 2013, 15(5): 752－760. (in Chinese with English abstract)

[23] Lowe D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91－110.

[24] Yastikli N. Documentation of cultural heritage using digital photogrammetry and laser scanning[J]. Journal of Cultural Heritage, 2007, 8(4): 423－427.

[25] 李能. 多基线普通数码相机近景摄影测量精度研究[D].昆明：昆明理工大学，2013.

[26] Alvarez-Mozos J, Verhoest N E, Larranaga A, et al. Influence of surface roughness spatial variability and temporal dynamics on the retrieval of soil moisture from SAR observations[J]. Sensors (Basel), 2009, 9(1): 463－489.

[27] Callens M, Verhoest N E C, Davidson M W J. Parameterization of tillage-induced single-scale soil roughness from 4-m profiles[J]. Ieee Transactions on Geoscience and Remote Sensing, 2006, 44(4): 878－888.

[28] Ogilvy J A, Foster J R. Rough surfaces-gaussian or exponential statistics[J]. Journal of Physics D-Applied Physics, 1989, 22(9): 1243－1251.

[29] Oh Y, Kay Y C. Condition for precise measurement of soil surface roughness[J]. Ieee Transactions on Geoscience and Remote Sensing, 1998, 36(2): 691－695.

[30] Nyquist H. Certain topics in telegraph transmission theory[J]. Transactions of the American Institute of Electrical Engineers, 1928, 47(2): 617－644.

[31] 李俐，王荻，潘彩霞，等. 基于神经网络与决策树的土壤粗糙度测量[J]. 农业工程学报，2015，31(14)：132－138.

Li Li, Wang Di, PanCaixia, et al. Soil surface roughness measuring method based on neural network and decision tree[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2015, 31(14): 132－138. (in Chinese with English abstract)

Improvement of soil surface roughness measurement accuracy by close-range photogrammetry

Tao Haoran1,2, Chen Quan2※, Li Zhen2, Zeng Jiangyuan2, Chen Xiaoning1
(1. College of Geomatics, Xi’an University of Science and Technology, Xi’an 710054, China; 2. Airborne Remote Sensing Center, Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100094, China)

Microwave remote sensing measurements are sensitive to surface parameters, and can be used for quantitative estimation of soil moisture, surface roughness and vegetation information. The ground-based true values of surface roughness parameters are important for the validation and accuracy evaluation of inversion results, and also vital in microwave soil moisture inversion algorithm for calibrating the constants in the model. For a long time, there is a lack of a simple, fast, high-precision method to obtain surface roughness parameters. Firstly, 2 commonly used parameters that characterize surface roughness i.e. root mean square height and correlation length, are described in this paper. Then, the concrete process of surface roughness measurement by close-range photogrammetry is introduced. We also analyze the factors which influence the measurement accuracy of close-range photogrammetry. In addition, close-range photogrammetry results are compared with the traditional pin-profiler method, and the measurement results of the root mean square height and correlation length of the 2 methods are analyzed. It is shown that the mean square root height error measured by the traditional pin-profiler method can reach is 12%-35.1%, and the correlation length error is 19.6%-62.4%. The advantages and disadvantages of the 2 methods are analyzed from the aspects of applicability and accuracy. The accuracy required for microwave inversion of surface roughness parameters is also analyzed. Result shows the way by close-range photogrammetry can improve the accuracy of surface roughness measurement effectively, and meet the requirements of inversion research of soil surface roughness. The influence of sampling interval on roughness measurement accuracy is also analyzed by changing the sampling interval of close-range photogrammetry. This article uses Agisoft Photoscan software to reconstruct point cloud. Specifically, a non-measuring camera is used to obtain multi-angle overlapping image of the study area. Secondly, SIFT (scale-invariant feature transform) approach is used to detect correspondences across the photos. Then bundle-adjustment algorithm is used to solve camera intrinsic and extrinsic orientation parameters and a multi-view approach is utilized to reconstruct dense cloud. Finally, the effect of non-contact measurement can be achieved by measuring the generated dense point cloud. This article also presents the requirements of hardware and image acquisition operations that need paid attention during the measurement of surface roughness using close-range photogrammetry. In this paper, the method of measuring surface roughness by close-range photogrammetry has the following advantages: The accuracy of surface roughness measurement is greatly improved, and the problem of certain surface which is extremely rough and can’t be measured is also solved. And the sampling interval of close-range photogrammetry is quantitatively analyzed. Close-range photogrammetric measurement can easily adjust the sampling angle and describe the anisotropy of surface roughness accurately. The number of sampling can be easily increased so as to solve the measurement error caused by the heterogeneity of the surface. At the same time, it is concluded that the measurement result is stable and can be regarded as the true value when the number of measurements is greater than 12. With the advantages of non-contact measurement, high precision, adjustable sampling interval and frequency, the close-range photogrammetric method provides an effective solution for soil surface roughness measurement.

remote sensing; roughness; measurements; close-range photogrammetry; dense cloud; sample interval

10.11975/j.issn.1002-6819.2017.15.021

P237

A

1002-6819(2017)-15-0162-06

2017-03-20

2017-05-11

国家重点研发计划项目（2016YFC1401006），国家自然科学青年基金（41601371），高分辨率对地观测系统重大专项（民用部分，03-Y20A11-9001-15/16）

陶浩然，男，主要从事雷达地表参数反演研究。西安 西安科技大学测绘科学与技术学院，710054。Email：414119940@qq.com

※通信作者：陈 权，男，副研究员，主要从事微波散射机理、地表参数反演等方面研究。北京 中国科学院遥感与数字地球研究所航空遥感中心，100094。Email：chenquan@radi.ac.cn