基于位移变化率和强度折减有限元的边坡失稳判定方法

江胜华，汪时机，李伟清，鲍安红

基于位移变化率和强度折减有限元的边坡失稳判定方法

江胜华，汪时机，李伟清，鲍安红

（西南大学工程技术学院，重庆 400715）

采用强度折减有限元法计算边坡稳定时，以变形为基础的失稳判据具有显著的物理意义和工程意义。该文采用变步长的折减方法，基于位移变化率-强度折减系数曲线的转折突变作为失稳判据，并研究特征点的敏感性及选取范围。计算结果表明，当折减系数为1.42时，坡顶水平位移变化率、竖向位移变化率和总位移变化率均发生急剧性的转折。与位移相比，位移变化率-强度折减系数的曲线存在明显的转折突变，可更准确、明显地判断边坡稳定的安全度。至坡顶一定距离范围内的特征点，如位于非塑性区域且非滑动土体时，其位移变化率-强度折减系数的曲线发生转折突变，但曲线在转折点附近存在振荡现象。通过位移变化率计算得到的54个安全系数，平均值为1.420，变异系数为0.005 3，不同特征点根据水平位移变化率、竖向位移变化率和总位移变化率得到的安全系数基本一致。当特征点至坡顶的距离≤1倍坡高时，特征点的位移＞12 mm，且位移变化率均较大，此时特征点对位移变化率较敏感；当特征点至坡顶的距离＞1倍坡高时，特征点位移在5～18 mm之间，但位移变化率大幅度降低，此时特征点对位移变化率的敏感性大幅度降低。考虑边界约束的影响及特征点的敏感性，建议特征点的选取范围为：与坡顶距离为1倍坡高的范围。

边坡稳定性；模型；边界条件；强度折减法；有限元法；位移变化率

江胜华，汪时机，李伟清，鲍安红. 基于位移变化率和强度折减有限元的边坡失稳判定方法[J]. 农业工程学报，2017，33(15)：155－161. doi：10.11975/j.issn.1002-6819.2017.15.020 http://www.tcsae.org

Jiang Shenghua, Wang Shiji, Li Weiqing, Bao Anhong. Slope instability evaluation method using finite element method of strength reduction and displacement rate[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(15): 155－161. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.15.020 http://www.tcsae.org

0 引 言

强度折减有限元法在边坡稳定计算中得到了广泛的应用，目前失稳判别准则主要有：1）在最大迭代次数内计算不能收敛[1-2]；2）从坡顶至坡脚发生广义剪应变贯通[3]；3）特征点位移的突变[4-9]；4）特征点位移增量与强度折减系数增量之比[10-11]；5）从坡顶至坡脚发生塑性区的贯通[12-13]；6）能量积分与折减系数关系曲线[14]。在边坡稳定的有限元计算中强度折减法和加载系数法本质上一致的[15-19]，强度折减有限元中随着强度折减系数的增加，边坡的变形发生改变，与荷载增加时变形改变是等效的，因此，强度折减有限元中位移随着强度折减系数的变化，具有一定的物理意义和工程意义。另一方面，现有边坡的实际监测工程中，获得的主要监测信息为边坡的变形[20]，如何建立边坡变形与稳定的安全度之间的联系，然后根据变形确定边坡稳定的安全系数并进行预警，具有重要的科学意义和工程意义[21]。因此，针对特征点位移的突变和特征点位移变化率的强度折减有限元法，由于具有明确的工程意义和物理意义，作为失稳判据具有显著的优点。

以坡顶、最大位移对应的节点等位置作为特征点，根据其水平位移、竖向位移、总位移等变形为标准，在理论上，当边坡达到极限状态时，特征点的位移将趋于流动状态，强度折减系数与位移的曲线发生突变，取对应的强度折减系数为安全系数[22]。但目前对于特征点位置的选取[22-24]、计算过程中强度参数折减的幅度[25]、水平位移和竖向位移的选取[5]、强度折减系数与位移的曲线拐点不明显时如何判断选择极限状态[23-24]等尚未取得共识，需要进一步的研究。

针对基于变形的强度折减有限元法，该文以边坡稳定计算为对象，深入探讨了基于位移变化率的强度折减有限元法，对于特征点的敏感性和选取范围及其影响进行了研究，同时分析了强度折减系数的折减幅度，讨论了基于位移变化率的强度折减有限元法的判别准则，比较了基于位移变化率的强度折减有限元法、计算不收敛和塑性区贯通等3种失稳判别准则，并对于基于位移变化率的强度折减有限元法给出了相关的建议。

1 基于位移变化率的强度折减有限元法

强度折减法是将土体的抗剪强度参数c和tanφ按等比例进行折减，折减后的强度参数为式中c和φ为土体的黏聚力（kPa）和内摩擦角(°)；K为强度折减系数。

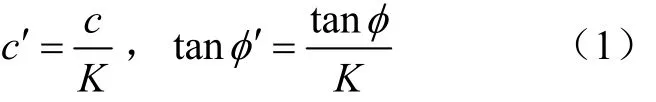
在标准三轴试验中，偏应力σ1-σ3与轴向应变ε的关系近似为[26-27]

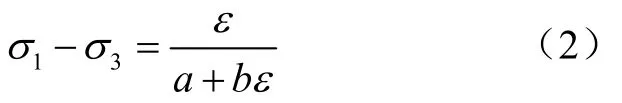
式中(σ1-σ3)f为土体破坏时的偏应力，kPa，Rf为破坏比，一般为0.75～1.0。

根据Mohr-Coulomb准则，土体破坏时的偏应力为

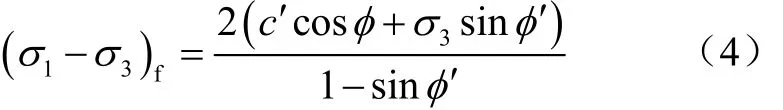
联立式（1）－式（4），则在标准三轴试验中，根据Mohr-Coulomb准则，土体破坏时的轴向应变εf与折减系数K的关系为

土体破坏时，轴向位移h相对于强度折减系数的变化率与应变的关系为

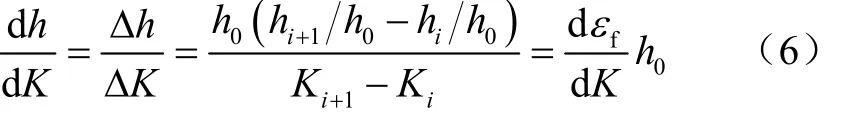
式中h0为土体试样的初始高度，mm，hi和hi+1分别为强度折减系数Ki和Ki+1时的极限轴向位移，mm。

以某土体试样为例，粘聚力c=42 kPa，内摩擦角φ=17°，Rf=1.0，Ei=200 MPa，在标准三轴试验中取σ1=500 kPa，σ3=300 kPa。根据式（1）－式（6），其应变及应变变化率与强度折减系数的关系见图1。图1中，强度参数的折减，采用0.1、0.01和0.001的变步长。

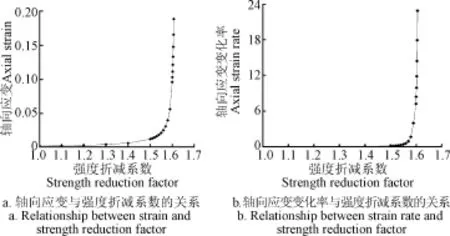
图1 应变和应变变化率与强度折减系数的关系Fig.1 Relationship between strain, strain rate and strength reduction factor

在土体的加载过程中，接近破坏时，能量耗散率逐渐增大。由图1可知，随着强度系数的折减，土体接近破坏，相对于强度折减系数的应变变化率dε/dK亦逐渐增大，在强度折减系数为1.58时，曲线发生转折突变。根据式（6），则位移变化率dh/dK亦随之增大，且曲线发生转折突变。

在边坡稳定的有限元计算中，根据连续介质的基本假定，在边界范围内节点的位移变化率与其他节点的位移变化率均存在一定程度的关联。在边坡稳定的强度折减过程中，塑性区的贯通会影响一定范围的土体，可认为在影响范围内节点的位移变化率dh/dK均发生转折突变。

2 计算分析

2.1 计算模型与计算流程

为便于分析讨论，取某土坡作为算例。该边坡的坡角为45°，斜坡部分高H为20 m，斜坡范围由2层土组成，各土层厚度均为10 m。上层：容重γ=20 kN/m3，弹性模量E=960MPa，泊松比μ=0.33，粘聚力c=36 kPa，内摩擦角φ=13°；下层：容重γ=25 kN/m3，弹性模量E= 1 000 MPa，泊松比μ=0.30，粘聚力c=42kPa，内摩擦角φ=17°。边坡长为105 m，高为40 m，坡脚至左边界的距离L=1.5H=30 m，坡顶至右边界的距离为R=55≥2.5H= 50 m，坡顶至底部边界的距离B=2H=40 m，满足边界范围的要求[28-30]。按照平面应变建立有限元计算模型，采用四边形一阶单元，四边形网格的长宽比为1.0～2.057，网格尺寸为1.375～2.828 m，网格尺寸与坡高（20 m）的比值为0.068 8～0.141。边界条件为：下部固定，左右两侧约束水平位移，上部为自由边界。计算模型见图2。

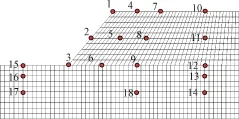
图2 边坡有限元模型Fig.2 Finite element model of slope

采用Fortran编制主程序，将有限元软件作为子程序进行调用，有限元软件通过批处理在后台运行。包括4个模块：1）主程序，为Fortran95格式，包含流程控制，根据强度折减系数调整抗剪强度参数，调用有限元计算，提取计算结果、处理计算结果等；2）强度折减有限元，为ANSYS的APDL文件，每一次计算时，自动读取抗剪强度参数，并输出计算结果；3）抗剪强度参数的外部文件；4）有限元计算结果的外部文件。在强度折减系数的搜索过程中，从1.0K=开始，采用0.1、0.01、0.001和0.000 1的变步长进行逼近，得到不收敛时对应的强度折减系数，并在此基础上，得到位移变化率与强度折减系数的关系，计算流程框图见图3。

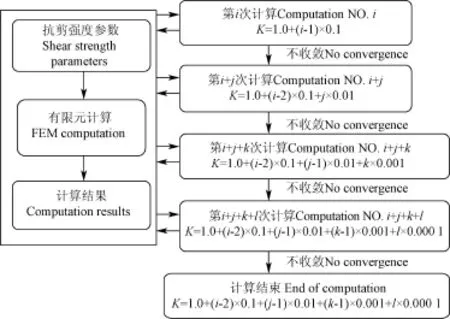
图3 强度折减系数的自动搜索流程图Fig.3 Flowchart of automatic searching for strength reduction factor

取边坡左下角为坐标原点，水平方向为x轴，竖向为y轴，选择18个特征点，其中坡面取3个特征点，P1(50,40)，P2(40,30)，P3(30,20)；滑动面附近取3个特征点，P4(60,40)，P5(50,30)，P6(45,20)；滑动面右侧一定范围选取3个特征点，P7(70,40)，P8(65,30)，P9(60,20)；坡顶右侧2倍坡高（2H=40）的断面取5个特征点，P10(90,40)，P11(90,30)，P12(90,20)，P13(90,16)，P14(90,10)；坡脚左侧1倍坡高（1.0H=20）的断面取3个特征点，P15(10,20)，P16(10,16)，P17(10,10)；至坡顶的竖直距离为1.5倍坡高（1.5H=30）的断面除P14(90,10)和P17(10,10)外，另取1个特征点，P18(60,10)。18个特征点的位置分布见图2。

2.2 坡顶位移、位移变化率与强度折减系数的分析

坡顶P1的位移和位移变化率随强度折减系数的变化曲线见图4，其中，ux、uy和u分别为水平位移、竖向位移和总位移，单位为mm，u˙x=duxd K、u˙y=duyd K和 u˙=dudK分别为水平位移变化率、竖向位移变化率和总位移变化率；K为强度折减系数。

由图4可知，坡顶的水平位移、竖向位移和总位移均随着强度折减系数的增大而增大，且增大的幅度逐渐提高，但没有明显的转折点或突变。坡顶的水平位移变化率、竖向位移变化率和总位移变化率均随着强度折减系数的增大而增大，且增大的幅度逐渐提高，在K=1.42时，水平位移变化率、竖向位移变化率和总位移变化率均发生急剧性的转折。可见，相比位移而言，位移变化率可更准确、明显地判断边坡稳定的安全度。

在K=1.43时，边坡的塑性区发生贯通；在K=1.433 7时，有限元计算不收敛。可见，位移变化率转折突变对应的强度折减系数，与塑性区贯通和计算不收敛的失稳判断基本一致。

本文中，边坡为沉陷式边坡，虽然以竖向位移为主，但坡顶的水平位移变化率、竖向位移变化率和总位移变化率与强度折减系数的曲线关系均发生转折突变，且对应的强度折减系数均为1.42。另一方面，由图4可知，边坡在临近失稳滑动时，强度折减系数极其微小地增加，均会引起位移变化率的大幅度增大，因此，在强度参数的折减过程中，强度折减系数的步长宜采用逐渐减小的变步长，且在临近失稳滑动时采用小步长。

图4 坡顶位移和位移变化率与强度折减系数的关系Fig.4 Relationship between displacement, displacement rate and strength reduction factor (P1)

2.3 特征点的选取范围及敏感性分析

为分析不同位置的特征点位移变化率与强度折减系数的关系，给出距离坡顶的竖直距离为1倍坡高（1.0H=20）的断面处P9，坡顶右侧2倍坡高（2H=40）的断面处P10和P14的总位移及总位移变化率随强度折减系数的关系，见图5。由于水平位移变化率、竖向位移变化率和总位移变化率随强度折减系数的关系基本一致，故图5仅给出了总位移及总位移变化率随强度折减系数的关系。在K=1.433 7时，边坡的剪应变增量分布图和位移向量场见图6。

图5 P9、P10、P14总位移和总位移变化率与强度折减系数的关系Fig.5 Relationship between total displacement, displacement rate and strength reduction factor (P9, P10, P14)

由图5可知，虽然P9距离坡顶的竖直距离为2倍坡高（2H=40），P10、P14距离坡顶的水平距离为2倍坡高（2H=40），P9、P10、P14均位于非塑性区域且非滑动土体，但其总位移变化率随强度折减系数的增大而增大；在强度折减系数为1.42时，P9、P14的位移变化率曲线发生转折突变，在强度折减系数为1.41时，P10的位移变化率曲线发生转折突变，但上述3个特征点的位移变化率-强度折减系数的曲线在转折点附近均存在振荡现象。同时，相对于特征点P1（坡顶）而言，P9、P10、P14的位移变化率大幅度降低。总体而言，随着强度折减系数的增大，在坡面或滑动面的一定距离范围内节点的位移变化率均存在转折突变，均可作为边坡失稳的判据之一。

由图6a可知，在K=1.433 7时，剪应变增量分布区域主要为塑性区。由图6b可知，在K=1.433 7时，在塑性区或滑动土体，特征点位移存在明显的滑动趋势。比较图6a和图6b可知，在非塑性区域且非滑动土体的特征点亦存在明显的总位移，由于该边坡为沉陷式边坡，以竖向位移为主，但至坡顶的距离越远则总位移越小。在18个特征点中，特征点1（即坡顶）的总位移最大，为20.23 mm，特征点17的总位移最小，为2.87 mm。

图6 极限状态时边坡的剪应变增量分布图和位移向量场Fig.6 Shear strain increment distribution and displacement vectorfield of slope in limit equilibrium state

根据18个特征点的水平位移变化率、竖向位移变化率和总位移变化率与强度折减系数的关系，通过曲线的转折突变可分别得到对应的强度折减系数，结果见表1。

表1 强度折减系数与位移变化率的关系Table 1 Relationship between strength reduction factor and displacement rate

由表1可知，大多数特征点，根据水平位移变化率、竖向位移变化率和总位移变化率得到的3个安全系数相等。同时，通过18个特征点的水平位移变化率、竖向位移变化率和总的位移变化率随着强度折减系数的曲线关系，可得到54个安全系数，其取值基本一致，平均值为1.420 2，变异系数为0.005 3，变异系数小于1%。另一方面，根据位移变化率得到的安全系数，略小于塑性区贯通对应的安全系数（1.43）及计算不收敛对应的安全系数（1.433 7）相比，误差为0.94%，基本一致。

为分析不同特征点的敏感性。由于最大的位移和最大的位移变化率均在坡顶附近，且鉴于坡顶位置的特殊性和显著性，视坡顶为最敏感的特征点。在K=1.4337时，分析其他特征点Pi(i=2,…,18)与坡顶P1的相对距离

与总位移u及总位移变化率dduuK=˙之间的关系，结果见图7。

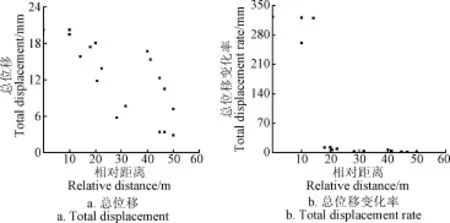
图7 特征点的相对距离与总位移、总位移变化率的关系Fig.7 Relationship between relative distance and total displacement, total displacement rate

由图7可得，在K=1.433 7时，当特征点至坡顶的距离≤20 m（1倍坡高1.0H=20）时，特征点的位移＞12 mm，且位移变化率较大，此时特征点对位移变化率较敏感；特征点至坡顶的距离＞20 m（1倍坡高1.0H=20）时，特征点位移在5～18 mm之间，但位移变化率大幅度降低，此时特征点对位移变化率的敏感性大幅度降低。由于强度折减系数有限元的最佳计算边界为，坡顶至右侧边界为2.5倍的坡高，坡脚至左侧边界为1.5倍的坡高，坡顶至底部边界为2倍的坡高[29-30]，根据上述的敏感性分析，且综合考虑边界约束的影响，建议特征点选取范围为：与坡顶的相对距离为1倍坡高的范围。

3 结 论

1）该文提出变步长的折减方法，基于位移变化率-强度折减系数曲线的转折突变作为失稳判据，并研究了特征点的选取范围。相比位移而言，位移变化率可更准确、明显地判断边坡稳定的安全度。

2）坡顶的水平位移、竖向位移和总位移均与强度折减系数的曲线关系，没有明显的转折点或突变。在强度折减系数为1.42时，坡顶水平位移变化率、竖向位移变化率和总位移变化率均发生急剧性的转折。

3）至坡顶一定距离范围内的特征点，如位于非塑性区域且非滑动土体，则其位移变化率-强度折减系数的曲线发生转折突变，但曲线在转折点附近存在振荡现象。通过位移变化率计算得到的54个安全系数，平均值为1.420，变异系数为0.005 3，不同特征点根据水平位移变化率、竖向位移变化率和总位移变化率得到的安全系数基本一致。

4）当特征点至坡顶的距离≤1倍坡高时，特征点的位移＞12 mm，且位移变化率均较大，此时特征点对位移变化率较敏感；当特征点至坡顶的距离＞1倍坡高时，特征点位移在5～18 mm之间，但位移变化率大幅度降低，此时特征点对位移变化率的敏感性大幅度降低。考虑有限元计算中边界约束的影响，结合特征点的敏感性，建议特征点的选取范围为：与坡顶相对距离为1倍坡高的范围。

[1] 赵尚毅，郑颖人，时卫民，等. 用有限元强度折减法求边坡稳定安全系数[J]. 岩土工程学报，2002，24(3)：343－346.

Zhao Shangyi, Zheng Yingren, Shi Weimin, et al. Analysis on safety factor of slope by strength reduction FEM[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(3): 343－346. (in Chinese with English abstract)

[2] Dawson Ethan, You Kwangho, Park Yeonjun. Strength-Reduction Stability Analysis of Rock Slopes Using the Hoek-Brown Failure Criterion[C]// Proceedings of Sessions of Trends in rock mechanics, Denver, Colorado, USA, Geo-Denver, 2014: 65－77.

[3] 连镇营，韩国城，孔宪京. 强度折减有限元法研究开挖边坡的稳定性[J]. 岩土工程学报，2001，23(4)：407－411.

Lian Zhenying, Han Guocheng, Kong Xianjing. Stability analysis of excavation by strength reduction FEM[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(4): 407－411. (in Chinese with English abstract)

[4] 宋二祥. 土工结构安全系数的有限元计算[J]. 岩土工程学报，1997，19(1)：1－7.

Song Erxiang. Finite element analysis of safety factor for soil structures[J]. Chinese Journal of Geotechnical Engineering, 1997, 19(1): 1－7. (in Chinese with English abstract)

[5] 葛修润，任建喜，李春光，等. 三峡左厂3#坝段深层抗滑稳定三维有限元分析[J]. 岩土工程学报，2003，25(4)：389－394.

Ge Xiurun, Ren Jianxi, Li Chunguang, et al. 3D-FEM analysis of deep sliding stability of 3# dam foundation of left power house of the Three Gorges Project[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(4): 389－394. (in Chinese with English abstract)

[6] 张强，葛修润，王水林，等. 考虑材料变形和破坏特性的强度折减方法研究[J]. 岩石力学与工程学报，2011，30(s1)：2764－2769.

Zhang Qiang, Ge Xiurun, Wang Shuilin, et al. Study of strength reduction method considering material deformation and failure characteristics[J]. Chinese Journal of Rock Mechanics & Engineering, 2011, 30(s1): 2764－2769. (in Chinese with English abstract)

[7] 宋琨，晏鄂川，毛伟，等. 广义Hoek-Brown准则中强度折减系数的确定[J]. 岩石力学与工程学报，2012，31(1)：106－112.

Song Kun, Yan Echuan, Mao Wei, et al. Determination of shear strength reduction factor for generalized Hoek-Browncriterion[J]. Chinese Journal of Rock Mechanics & Engineering, 2012, 31(1): 106－112. (in Chinese with English abstract)

[8] 李翠华，姜清辉，周创兵. 强度折减有限元法中的单元阶次影响分析[J]. 岩土力学，2013，34(11)：3315－3320.

Li Cuihua, Jiang Qinghui, Zhou Chuangbing. Effect of element order on strength reduction finite element method[J]. Rock and Soil Mechanics, 2013, 34(11): 3315－3320. (in Chinese with English abstract)

[9] Liu Jian, Shang Ke, Wu Xing. Stability analysis and performance of soil-nailing retaining system of excavation during construction period[J]. Journal of Performance of Constructed Facilities, 2016, 30(1): C4014002.

[10] 迟世春，关立军. 应用强度折减有限元法分析土坡稳定的适应性[J]. 哈尔滨工业大学学报，2005，37(9)：1298－1302. Chi Shichun, Guan Lijun. Soil constitutive equation for slope stability by finite element method with discount shear technology[J]. Journal of Harbin institute of technology, 2005, 37(9): 1298－1302. (in Chinese with English abstract)

[11] 迟世春，关立军. 基于强度折减的拉格朗日差分方法分析土坡稳定性[J]. 岩土工程学报，2004，26(1)：42－46.

Chi Shichun, Guan Lijun. Slope stability analysis by Lagrangian difference method based on shear strength reduction[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(1): 42－46. (in Chinese with English abstract)

[12] 王栋，年廷凯，陈煜淼. 边坡稳定有限元分析中的三个问题[J]. 岩土力学，2007，28(11)：2309－2313.

Wang Dong, Nian Tingkai, Chen Yumiao. Three problems in slope stability analyses with finite element method[J]. Rock and Soil Mechanics, 2007, 28(11): 2309－2313. (in Chinese with English abstract)

[13] Wang Wei, Yuan Wei, Li Xiaohun, et al. Evaluation Approach of the Slope Stability Based on Deformation Analysis[J]. International Journal of Geomechanics, 2016, 16(2): 04015054

[14] 施建勇，曹秋荣，周璐翡. 修正有限元强度折减法与失稳判据在边坡稳定分析中的应用[J]. 岩土力学，2013，34(s2)：237－241.

Shi Jianyong, Cao Qiurong, Zhou Lufei. Modified finite element method for shear strength reduction and instability Criterion in slope stability analysis[J]. Rock and Soil Mechanics, 2013, 34(s2): 237－241. (in Chinese with English abstract)

[15] 曹建建，邓安. 离心加载有限元方法在边坡稳定分析中的应用[J]. 岩土工程学报，2006，28(s)：1336－1339.

Cao Jianjian, Deng An. Centrifugal loading finite element method for slope stability analysis[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(s): 1336－1339. (in Chinese with English abstract)

[16] 郑颖人. 岩土材料屈服与破坏及边（滑）坡稳定分析方法研讨：三峡库区地质灾害专题研讨会”交流讨论综述[J].岩石力学与工程学报，2007，26(4)：649－661.

Zheng Yingren. Discussion on yield failure of geomaterials and stability analysis methods of slope/landslide: Communication and discussion summary of special topic forum on geologic disasters in the three gorges project[J]. Chinese Journal of Rock Mechanics & Engineering, 2007, 26(4): 649－661. (in Chinese with English abstract)

[17] 李焕强，孙红月，尚岳全，等. 有限元离心加载法分析边坡稳定性[J]. 江南大学学报：自然科学版，2008，7(5)：595－598.

Li Huanqiang, Sun Hongyue, Shang Yuequan, et al. Study on slope stability by centrifuge loading FEM[J]. Journal of Jiangnan University: Natural Science Edition, 2008, 7(5): 595－598. (in Chinese with English abstract)

[18] 张嘎，王爱霞，牟太平，等. 边坡破坏过程离心模型试验的应力位移场研究[J]. 岩土力学，2008，29(10)：2637－2641.

Zhang Ga, Wang Aixia, Mu Taiping, et al. Study of stress and displacement fields in centrifuge modeling of slope progressive failure[J]. Rock and Soil Mechanics, 2008, 29(10): 2637－2641. (in Chinese with English abstract)

[19] 金华. 边坡稳定分析的加载系数法[D]. 银川：宁夏大学，2013.

Jin Hua. Slope Stability Analysis of the Load Coefficient Method[D]. Yinchuan: Ningxia University, 2013. (in Chinese with English abstract)

[20] 张晓平，吴顺川，王思敬. 类土质路堑边坡动态监测及数值模拟分析[J]. 岩石力学与工程学报，2008，27(s2)：3431－3440.

Zhang Xiaoping, Wu Shunchuan, Wang Sijing. Dynamic monitoring and numerical analysis of soil-like cut slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(s2): 3431－3440. (in Chinese with English abstract)

[21] 杨光华，张玉成，张有祥. 变模量弹塑性强度折减法及其在边坡稳定分析中的应用[J]. 岩石力学与工程学报，2009，28(7)：1506－1512.

Yang Guanghua, Zhang Yucheng, Zhang Youxiang. Variable modulus elastoplastic strength reduction method and its application to slope stability analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(7): 1506－1512. (in Chinese with English abstract)

[22] 郑宏，刘德富. 弹塑性矩阵Dep的特性和有限元边坡稳定性分析中的极限状态标准[J]. 岩石力学与工程学报，2005，24(7)：1099－1105.

Zheng Hong, Liu Defu. Properties of elasto-plastic matrix Dep and a criterion on limiting state of slope stability by FEM[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(7): 1099－1105. (in Chinese with English abstract)

[23] 李维朝，戴福初，李宏杰，等. 基于强度折减法的岩质开挖边坡加固效果三维分析[J]. 水利学报，2008，39(7)：877－882.

Li Weichao, Dai Fuchu, Li Hongjie, et al. Three-dimensional analysis on reinforcement effect of excavated rocky slope based on strength reduction technique[J]. Journal of Hydraulic Engineering, 2008, 39(7): 877－882. (in Chinese with English abstract)

[24] 陈菲，邓建辉. 岩坡稳定的三维强度折减法分析[J]. 岩石力学与工程学报，2006，25(12)：2546－2551.

Chen Fei, Deng Jianhui. Three-dimensional stability analysis of rock slope with strength reduction method[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(12): 2546－2551. (in Chinese with English abstract)

[25] 梁庆国，李德武. 对岩土工程有限元强度折减法的几点思考[J]. 岩土力学，2008，29(11)：3053－3058.

Liang Qingguo, Li Dewu. Discussion on strength reduction FEM in geotechnical engineering[J]. Rock and Soil Mechanics, 2008, 29(11): 3053－3058. (in Chinese with English abstract)

[26] Duncan J M, Chang C Y. Nonlinear analysis of stress and strain in soils[J]. Journal of the Soil Mechanics and Foundations Division, 1970, 96(SM5): 1629－1653.

[27] Duncan J M, Byrne P, Wong K S, et al. Strength, stress-strain and bulk modulus parameters for finite element analysis of stresses and movements in soil masses[R]. Report No. UCB/GT/80-01, Dept. Civil Engineering, U.C. Berkeley, 1980.

[28] 郑颖人，赵尚毅，张鲁渝. 用有限元强度折减法进行边坡稳定分析[J]. 中国工程科学，2002，4(10)：57－61.

Zheng Yinren, Zhao Shangyi, Zhang Luyu. Slope stability analysis by strength reduction FEM[J]. Engineering Science, 2002, 4(10): 57－61. (in Chinese with English abstract)

[29] 张鲁渝，郑颖人，赵尚毅，等. 有限元强度折减系数法计算土坡稳定安全系数的精度研究[J]. 水利学报，2003(1)：21－27.

Zhang Luyu, Zheng Yingren, Zhao Shangyi, et al. The feasibility study of strength2reduction method with FEM for calculating safety factors of soil slope stability[J]. Journal of Hydraulic Engineering, 2003(1): 21－27. (in Chinese with English abstract)

[30] 万少石，年廷凯，蒋景彩，等. 边坡稳定强度折减有限元分析中的若干问题讨论[J]. 岩土力学，2010，31(7)：2283－2288.

Wan Shaoshi, Nian Tingkai, Jiang Jingcai, et al. Discussion on several issues in slope stability analysis based on shear strength reduction finite element methods (SSR-FEM)[J]. Rock and Soil Mechanics, 2010, 31(7): 2283－2288. (in Chinese with English abstract)

Slope instability evaluation method using finite element method of strength reduction and displacement rate

Jiang Shenghua, Wang Shiji, Li Weiqing, Bao Anhong
(College of Engineering and Technology, Southwest University, Chongqing 400715, China)

Finite element method of strength reduction is an important and effective measure to evaluate the stability safety of geotechnical engineering. Also, finite element method of strength reduction is widely used in slope stability computation, and failure criterion using deformation has obvious significance in aspects of physical and engineering meaning. However, there is no consensus among researchers regarding location selection of critical points, step-size of strength reduction, determination from horizontal displacement, vertical displacement and total displacement. Also, there is no consensus with regard to how to judge the limit state of slope when there is no obvious knee point on the curve of displacement versus strength reduction factor. The strength reduction of variable step-size is proposed in the paper. The curves of displacement, displacement rate versus strength reduction factor, are calculated automatically with the main program of Fortran and subroutine program of ANSYS software. The knee point on curve of displacement rate versus strength reduction factor is chosen as the failure criterion, and the sensitivity and location range of critical points are also studied. When strength reduction factor is 1.42, there is definite and specific knee point on curve of horizontal displacement rate, vertical displacement rate and total displacement rate of slope top versus strength reduction factor, which shows displacement rate is more accurate and sensitive than displacement in terms of slope failure criterion. When the critical point is in the vicinity of slope top and it is not located in plastic zone or sliding soil mass, there is also abrupt turning on the curve of displacement rate versus strength reduction factor with oscillation phenomenon although the critical points are relatively far from the slope point; and the corresponding safety factor is also about 1.42. Eighteen critical points are selected from different locations of slope, and by means of curves of horizontal displacement rate, vertical displacement rate and total displacement rate versus strength reduction factor, 54 safety factors are obtained. Consequently, the mean value of 54 safety factors is 1.420 and the variation coefficient is 0.005 3, which show that different critical points have nearly same safety factors and there is little difference between safety factors judged by horizontal displacement rate, vertical displacement rate or total displacement rate. When the distance from critical point to slope top is smaller than 20 m, about the height of slope, the total displacement of critical point is larger than 12 mm and the total displacement rate is large, which indicate that the critical points have high sensitivity. When the distance from critical point to slope top is larger than slope height, the total displacement of critical point ranges from 5 to 18 mm but the total displacement rate decreases drastically, which show that the critical points are also not sensitive either. Considering the influence of boundary range and the critical points’ sensitivity, it is suggested that the distance from the critical points to slope top should be less than the slope height. The step-size of strength reduction should be decreased gradually and small step-size should be used when the slope deformation is close to instable sliding.

slope stability; models; boundary conditions; finite element method; strength reduction method; displacement rate

10.11975/j.issn.1002-6819.2017.15.020

TV871

A

1002-6819(2017)-15-0155-07

2017-02-21

2017-07-13

国家自然科学基金（51208078，11572262）；重庆市前沿与应用基础研究计划（cstc2015jcyjA30008）；中央高校基本科研业务费专项资金（XDJK 2015B007）

江胜华，男，湖北仙桃人，副教授，博士，主要从事岩土工程监测与安全评价等领域的研究。重庆 西南大学工程技术学院，400715。

Email：jiangsh@whu.edu.cn