高背景下的二次函数问题
2017-09-15赵碧波仙居中学浙江仙居317300
●赵碧波 (仙居中学,浙江 仙居 317300)
高背景下的二次函数问题
●赵碧波
(仙居中学,浙江 仙居 317300)
二次函数是初、高中数学课程最重要的函数模型之一,它是连接函数、方程、不等式的桥梁,是渗透数学思想方法、提高学生思维与运算能力的主要载体,是学考、高考和数学联赛一试的热点、难点.因此,有必要从高等数学的角度研究二次函数的一些性质.
切比雪夫多项式;最值;反思;数学本质
二次函数问题内容丰富多彩,解题方法灵活多样.某些二次函数经过“华丽”的包装后,常让人感到模棱两可、困难倍增.下面通过具体的问题探究其背后所隐藏的数学本质.
1 基本题型
例1[1]求函数f(x)=|x2-a|在区间[-1,1]上的最大值M(a)的最小值.
解 因为函数f(x)=|x2-a|(其中x∈[-1,1])的对称轴为x=0,则
M(a)=max{f(-1),f(1),f(0)},
从而 2M(a)≥f(1)+f(0)≥|(1-a)+a|=1,
即


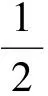
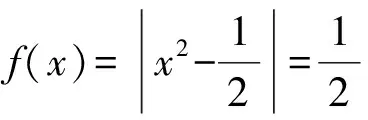
上式本质上就是一个二次型切比雪夫多项式.
切比雪夫多项式是高等数学中的内容,该问题的立意是高等的,而解法是初等的.命题者通过这种高背景下的问题考查学生对知识的掌握程度和学习潜能,学生若具备相关初等数学知识的能力、分析问题的能力,则思维上的障碍较少.
2 提炼升华,揭示数学本质
下面先给出二次型切比雪夫多项式的两个性质.
性质1[3]设二次函数f(x)=ax2+bx+c,若对任意的x∈[-1,1],|f(x)|≤1,则|a|max=2.

性质1的证明 由|f(-1)|=|a-b+c|≤1,|f(1)|=|a+b+c|≤1,|f(0)|=|c|≤1,知
4≥ |f(-1)|+|f(1)|+2|f(0)|≥
|(a-b+c)+(a+b+c)-2c|=|2a|,
则|a|≤2.当a=2,b=0,c=-1,即f(x)=2x2-1时,等号成立,故|a|max=2.
注f(x)=2x2-1其实就是二次切比雪夫多项式(T2(x)=2x2-1),其中x∈[-1,1].
M≥|f(-1)|=|1-b+c|,
M≥|f(1)|=|1+b+c|,
M≥|f(0)|=|c|,
从而 4M≥ |f(-1)|+|f(1)|+2|f(0)|≥
|(1-b+c)+(1+b+c)-2c|=2,
于是


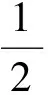
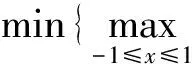
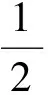
g(x)=x2+b0x+c0,x∈[-1,1],


从而



记h(x)=f(x)-g(x),则函数h(x)满足如下条件:



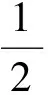

3 初级变形
例2 设函数f(x)=|x2+ax+b|(其中a,b∈R).若对任意的a,b∈R,总存在x0∈[0,4],使得f(x0)≥m,则实数m的取值范围是
( )
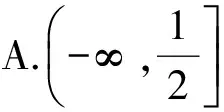
C.(-∞,2]D.(-∞,4]
(2017年3月浙江省学考十校联盟适应性考试第18题)
f(x)= |x2+ax+b|=
根据性质2知
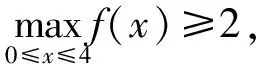
于是
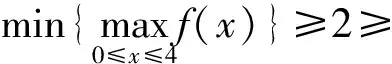

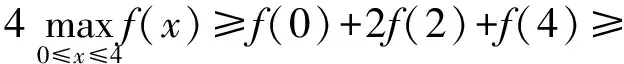
|b-2(4+2a+b)+(16+4a+b)|=8,
从而

当a=-4,b=2时,等号成立.
注 由性质2的证明过程,例2只需考虑f(0),f(2),f(4)即可.
4 高级变形
例3 已知a,b,c∈R,f(x)=ax2+bx+c,当0≤x≤1时,|f(x)|≤1,求|a|+|b|+|c|的最大值.
c=f(0).
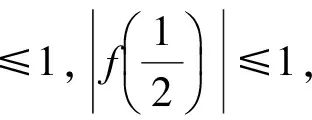
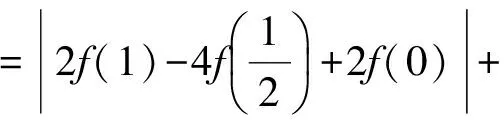

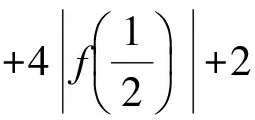

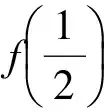
一般地,可以考虑f(0),f(t),f(1),其中0 c=f(0). 因为|f(1)|≤1,|f(t)|≤1,|f(0)|≤1,所以 |t2f(1)|+|-f(t)|+|(1-t2)f(0)|]+|f(0)|≤ 例4 函数f(x)=ax3+bx2+cx+d(其中a≠0),当0≤x≤1时,|f′(x)|≤1,试求a的最大值. (2010年全国高中数学联赛第9题) 解 因为f′(x)=3ax2+2bx+c,所以 f′(1)=3a+2b+c. 要求a,则必须消去参数b,c,从而 于是 例5 已知函数f(x)=x2+ax+b(其中a,b∈R),记M(a,b)是|f(x)|在区间[-1,1]上的最大值. 1)证明:当|a|≥2时,M(a,b)≥2; 2)略. (2015年浙江省数学高考理科试题第18题) 1)证明 由题意知|f(-1)|=|1-a+b|,|f(1)|=|1+a+b|,|f(0)|=|b|.要用条件|a|≥2,则必须消去参数b,从而 2M(a,b)≥ |f(-1)|+|f(1)|≥ |(1-a+b)-(1+a+b)|=|2a|≥4, 于是 M(a,b)≥2. 通过上述相关例子的设计与解析,我们清晰地看到隐藏在这类二次函数问题中一些形异而质同的数学本质.作为一线教师,针对某些问题,我们要多进行研究与反思,尝试从高等数学的角度揭示问题背后的本质.“授人以鱼,不如授人以渔”,让学生从本源上理解问题,对这类问题,才能如鱼得水,游刃有余. [1] 蔡小熊,孙惠华.新课标高中数学竞赛通用教材(高一分册)[M].杭州:浙江大学出版社,2013. [2] 刘云章,赵雄辉.数学解题思维策略——波利亚著作选讲[M].长沙:湖南教育出版社,1991. [3] 陈科钧.2类切比雪夫多项式性质的证明与应用[J].中学教研(数学):2017(2):45-48. 2017-05-30 赵碧波(1982-),男,浙江仙居人,中学一级教师.研究方向:数学教育. O122.1 A 1003-6407(2017)09-29-03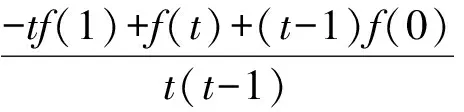
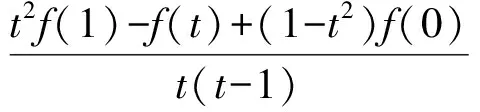
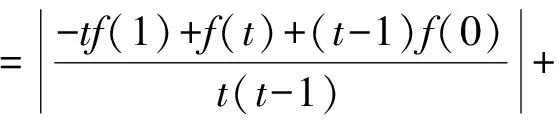

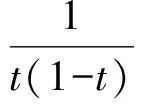
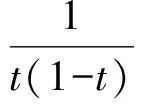


5 综合应用