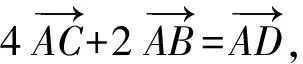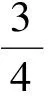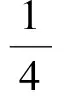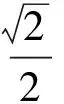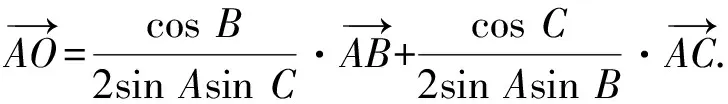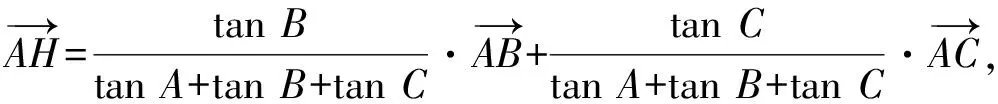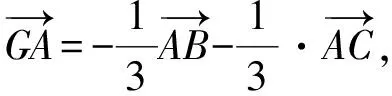不应排斥学科渗透问题的适度考查
2017-09-15刘海滨盐城中学江苏盐城224005
●刘海滨 (盐城中学,江苏 盐城 224005)
不应排斥学科渗透问题的适度考查
●刘海滨
(盐城中学,江苏 盐城 224005)
拓展数学应用,让学生学有用的数学,即学以致用,应是我们教学的一个重要目标.因此,高考应有正确的导向,不应固化考题,也不应排斥学科渗透问题的考查.只有多元化评价学生,考查学生的应用分析能力,这样才能调动教师开展研究性活动课的积极性,才能拓展学生的数学应用能力,才能真正提高学生的数学素养.
不应排斥;学科渗透;适度考查
1 问题背景
前不久,笔者所在学校高三年级组织了一次检测考试,数学试卷中有一道不同寻常的试题:
例1 如图1,一根细绳穿过2个等高的定滑轮,且2端分别挂有3 N,2 N的重物.现在2个定滑轮之间的细绳上挂一个重量为mN的重物,恰好使整个系统处于平衡状态,摩擦力忽略不计.
1)若细绳被重物拉成120°的夹角,求m的值;
2)求m的取值范围.

图1 图2
该检测题颇受争议,笔者所在学校高三数学组的主流意见是:把物理学科中的力学问题,融入到数学应用题中,难度较大,学生难以理清有关力的一些数量关系,而且数学高考肯定不会考查有关物理方面的应用题,平时的数学练习还是应该尽量避免此类题目.
上述意见,笔者不能完全苟同,有下列疑问:数学测试真的不能考查有关物理方面的应用题吗?我们的高考一定不允许学科渗透的考查吗?带着疑问,笔者做了一点思考,整理成文,与读者交流、探讨.
2 解题分析
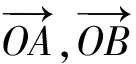
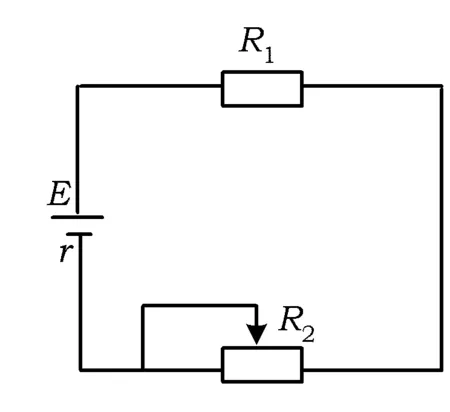
接下来就是图形中边角关系的研究.第1)小题中,120°的夹角即∠AOB,从而∠A=60°,在△AOC中运用余弦定理,即可求出m的值;对于第2)小题,很多学生在△AOC中运用三角形的三边关系,迅速得到1 根据实际情况,重物将细绳向下拉,α,β应都是锐角,易知∠ACO=β.在△AOC中,由正弦定理可得 3sinα=2sinβ, 2个式子相加,化简得 m=3cosα+2cosβ. 结合上述正弦等式,消去α,可得 可能有人认为:2次运用余弦定理的运算处理有点灵活,学生不易过关.确实如此,但这类问题在物理学科中,通常是由水平方向的合力为0,即由正弦定理可得3sinα=2sinβ;以及竖直方向的合力为0,从而直接得出m=3cosα+2cosβ.如此,很容易想到消角,转化为m关于β的函数. 对于例1,也许有人会说,它是一道物理题,不是数学题.说例1是物理题,肯定没有错,它就是日常生活中的滑轮问题,确实是物理方面的问题.但说它不是数学题,值得商榷! 要用一个标准严格界定一个问题是不是数学题,不是一件容易的事,但我们可以粗略地把数学题分为2大类:一类是纯粹的数学问题,以研究空间形式和数量关系为主(百度百科释义);另一类是数学应用问题,主要是运用数学知识解决生产、生活中的实际问题,即我们常讲的数学建模.据此,我们可以认为例1是数学应用题,只不过它是与力有关的问题,虽然是物理问题,但这并不妨碍它作为数学题.其实,数学与物理本来就是一家,没有数学理论知识作支撑,能研究物理问题吗?比如向量的引入,就源自于力学[1].数学就是解决实际问题(包括物理问题)的一个工具,从某种程度上讲,物理问题就是一类特殊的数学应用题. 回顾上述例1的解题过程,只是用了一点力的合成知识而已,而且这与数学中的向量加法是一致的,完成求解的主体过程是三角函数等数学知识,因此其作为数学题,不为过.若对于某一个问题的解决,所需物理知识的比重很大,远远多于数学知识,则把它作为数学题,就有点不合适了. 图3 翻开苏教版高中教材《数学(必修4)》,笔者发现:在“向量的应用”这节内容中,上述例1就是由课本题改编而来的(是在课本题的基础上,增加了第1)小题).并且类似于例1这样的“力与运动”方面的题目还有6道,笔者在此不一一例举[1].另外,在《数学(必修5)》“基本不等式”这节内容中,也有2道有关物理方面的题目:一道是杠杆问题[2],另一道是电学问题(即以下例2). 例2 如图3,电路中电源的电动势为E,内电阻为r,R1为固定电阻,R2为一个滑动变阻器.R2调至何值时,其消耗的电功率P最大?最大电功率是多少(其中P=I2R)? 此外,在《数学(必修1)》“函数模型及其应用”一节中,有物理冷却问题;在《数学(选修2-2)》“导数及其应用”一章中,有不少物理方面的问题.教材上这么多物理方面的应用问题说明:应充分关注数学应用教学,不应忽视数学知识在物理方面的应用,不应排斥学科渗透问题的考查. 4.1 不应固化考题 对于高考,笔者总是觉得过于保守了,试卷的固化太严重.高考之前给每个学生发《考试说明》,而根据《考试说明》命制的试卷,教师基本上都能估计到“什么题号对应什么题型,是什么难度”. 这样的试卷,对高中教学的影响比较大,不考的不教、必考的重点,反复讲反复练,课堂目标明确、重点突出,其实就是应试教学!教材上的阅读材料,没空读;教材上的探究问题,没空探.这样的教学,有点像工厂生成模具,所教出来的学生,都限制在一定的知识水平内,不能使学生学有所长,学生的个性化发展很差. 笔者认为:我们的高考不应固化考题,为什么要限制考题数量?完全可以根据试题难度调整数量,保证大多数学生有思考完成的时间即可.为什么要规定重要考点?文献[3]指出:高考应有正确的导向,有必要增加研究型试题,多元化评价学生,考查学生的研究分析能力,这样才能真正改变广大教师的守旧认识,调动教师积极开展研究性活动课,拓展学生的知识面,提高学生深入研究问题的能力,为教育创新起引领作用.总之,不限制考试思路,才能打开教学思路,才能让教师各尽其才,教出有深度和广度的学生. 4.2 应拓展数学应用 在平日的教学中,教师之间也常交流数学学习的作用,普遍认为:数学的学习能使人变得更聪明,它能锻炼人的思维分析能力,对今后的工作生活有着潜移默化的影响,而且数学是将来从事理工科工作人群的必要基础知识,是高端科研的必要知识. 笔者认为:中学数学教学应拓展数学应用,要让学生学有用的数学,要让我们的日常生活充满数学.当这些学生步入社会,即使不从事理工科的工作研究,他们也感到数学是有用的,并能把数学知识用到工作、生活中,这样我们的数学学习才更有意义,也才能让全社会都认同数学学习. 学习数学的目的是要让学生学有所用,解决生活中的实际问题,而不要刻意加大难度,反而有些生活问题,适当简化命题,倒是很有必要.没有必要排斥学科渗透问题的应用,而应该扩充数学应用的范围,加大数学应用题的考查,从而真正提高教师的应用教学意识,切实提高学生的数学建模能力. 高考命题要有原则,原则是要有正确的教学导向作用,要引导教师遵守教学理念,发挥自身所长,不仅要教给学生课本知识,更要教出自己的理解与观点,带领学生开展研究性学习活动,让学生学会思考,学会独立解决问题. [1] 单墫.普通高中课程标准实验教科书·数学(必修4)[M].南京:江苏教育出版社,2012. [2] 单墫.普通高中课程标准实验教科书·数学(必修5)[M].南京:江苏教育出版社,2012. [3] 崔志荣.高考数学应适当增加“研究型试题”的分析[J].数学通讯,2017(2):8-13. 若按顺时针排列,则 图1 如图1所示,将三角形所在平面分成7个区域,文献[1]和文献[2]已经证明了点O在△ABC内部(即区域①)的情形. 1)若点O在区域②内,则τ(A,BC,O)=-1,τ(B,CA,O)=-1,τ(C,AB,O)=-1,此时点O,B,C按顺时针排列,点O,C,A和点O,A,B按逆时针排列,从而 2)若点O在线段BC上(不含端点),则点O,B,C共线,进一步有x2y3=x3y2.此时,τ(A,BC,O)=0,τ(B,CA,O)=1,τ(C,AB,O)=1,点O,C,A和点O,A,B按顺时针排列,从而 同理可得 我们还可以把定理1阐述如下: 根据前面的定理,结合三角形“五心”的几何特征,可以得出一些等式,根据文献[1]的结论,下面的各个推论也只需对于钝角三角形的情形作出证明. 图2 图3 推论2 如图2,点O1,O2,O3是△ABC的旁心,则 证明 若△ABC为钝角三角形(其中∠C为钝角),则垂心O在三角形的外部(如图3),根据定理1可得 因为 即 S△OBC∶S△OCA∶S△OAB=tanA∶tanB∶(-tanC), 所以 图4 证明 若△ABC为钝角三角形(其中∠C为钝角),则外心O在三角形的外部(如图4),根据定理1可得 因为S△OBC=2R2sin∠BOC,S△OCA=2R2sin∠COA,S△OAB=2R2sin∠AOB,所以 又∠BOC=2A,∠COA=2B,∠AOB=2∠D=2(π-∠C),故 从上可以看出,三角形外心、内心、垂心的向量表示形式都与三角函数相关,且锐角三角形和钝角三角形的情形完全一致,简洁实用,可谓珠联璧合,给人以美的享受!如果改用三角形的边或面积来表示,则需要分情况讨论,达不到这个效果. (2014年浙江省高中数学竞赛试题第12题) (2016年全国高中数学联赛山东赛区预赛试题第5题) 以上3个例题都涉及到点在三角形外部的情形. sinA∶sinB∶sinC=2∶2∶1, tanA∶tanB∶tanC=1∶2∶3. 例6 (欧拉线)设△ABC的外心为O,重心为G,垂心为H,则点O,G,H共线. 证明 对于直角三角形,结论是显然的.对于非直角三角形,由推论4可得 故 即点O,G,H共线. 以上3个例题利用三角形“五心”统一向量表示形式,解题过程十分简单. 三角形的“五心”既有统一的向量表示形式,又有关乎三角形各角的等量关系,易于记忆,方便使用,在解决此类问题时还可以达到“秒杀”的效果. 参 考 文 献 [1] 朱庆华.面积法求三角形的五心的向量表示的同一形式[J].数学通讯,2010(5):40-41. [2] 关丽娜,钟德光.三角形“五心”向量形式的一个简证及应用[J].中学教研(数学),2017(1):31-34. [3] 克莱因.高观点下的初等数学·几何[M].上海:复旦大学出版社,2007. 2017-04-24 刘海滨(1969-),男,江苏盐城人,中学高级教师.研究方向:数学教育. O12 A 1003-6407(2017)09-32-03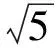
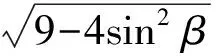
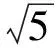
3 题类探讨
4 学以致用
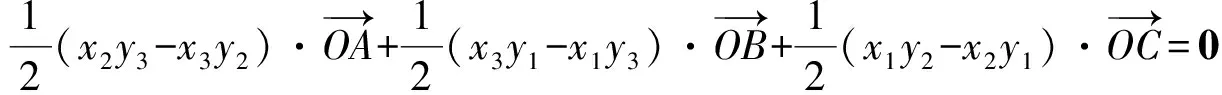
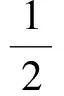


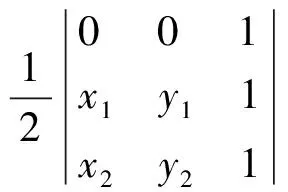


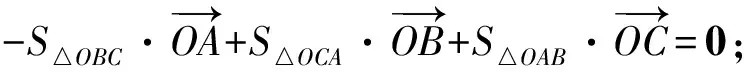
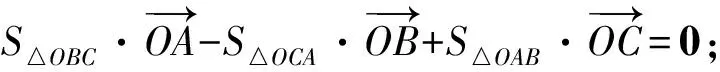

2 三角形的“五心”
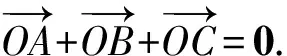

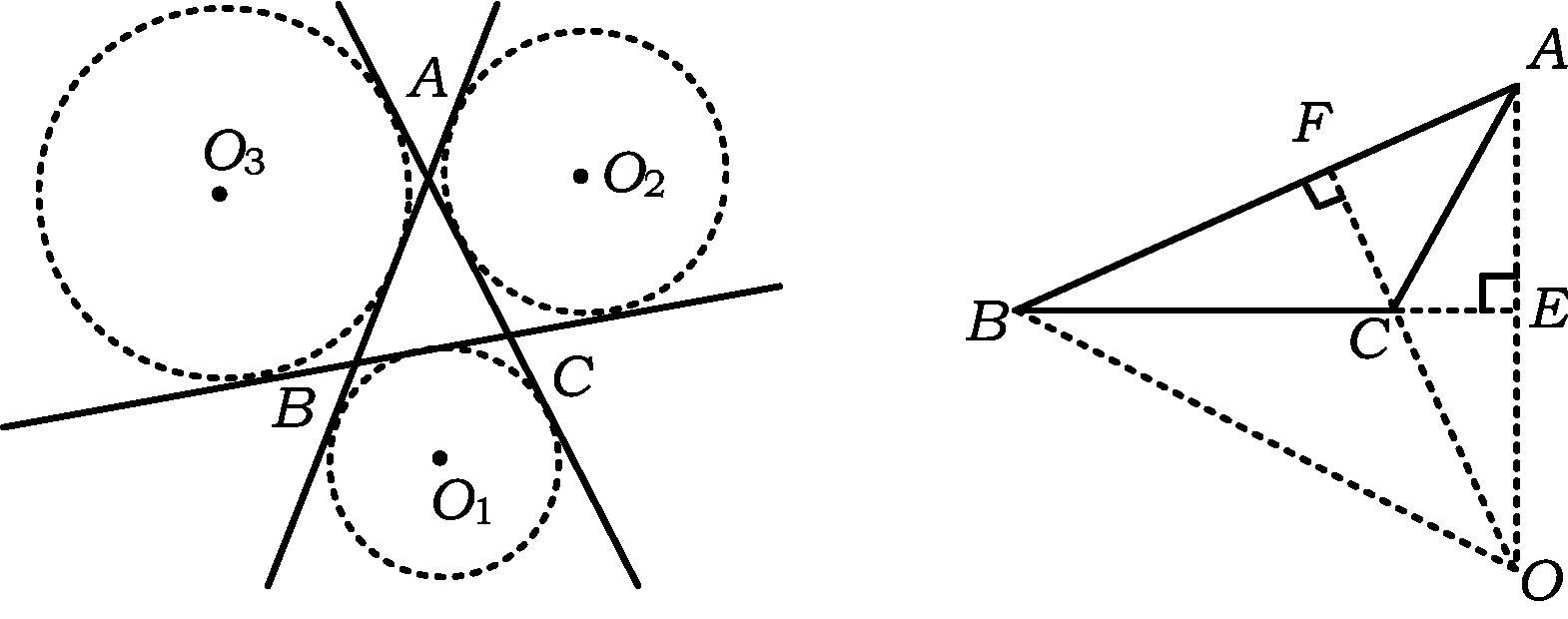
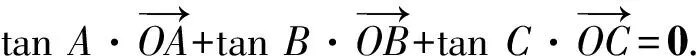

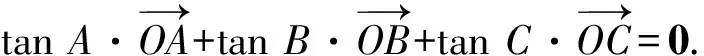
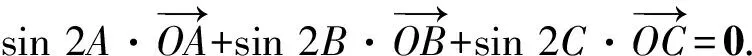
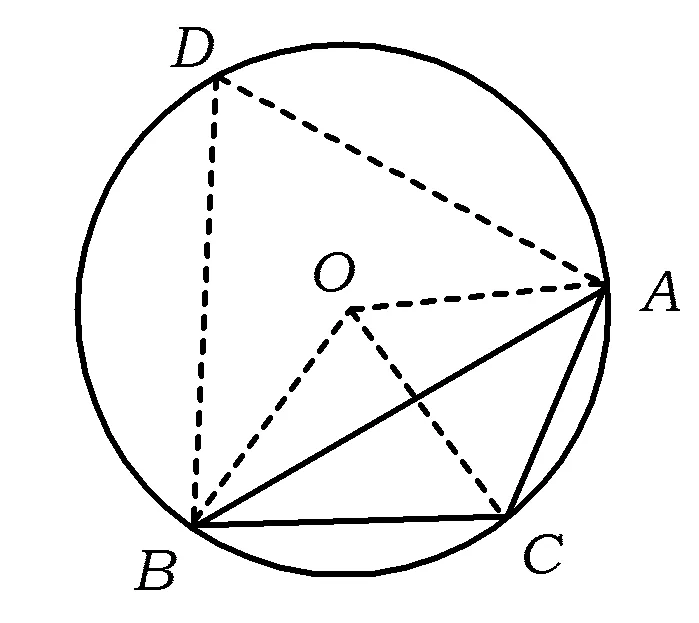
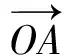

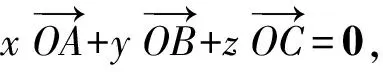

3 解题中的应用