基于多属性决策的机会传感器网络关键节点预测
2017-09-15刘琳岚孟令冲
刘琳岚 张 江 舒 坚 郭 凯 孟令冲
1(南昌航空大学信息工程学院 南昌 330063)2 (南昌航空大学软件学院 南昌 330063)
基于多属性决策的机会传感器网络关键节点预测
刘琳岚1张 江1舒 坚2郭 凯1孟令冲1
1(南昌航空大学信息工程学院 南昌 330063)2(南昌航空大学软件学院 南昌 330063)
(liulinlan@nchu.edu.cn)
提前获知或预测网络的关键节点,便可根据关键节点的相关信息对网络进行优化,当网络瘫痪时,可第一时间排查关键节点,减少网络维护时间和成本.现有静态无线传感器网络关键节点预测方法,不适用于机会传感器网络(opportunistic sensor networks, OSNs).针对机会传感器网络结构动态变化、消息传输时延高的特点,分析多区域机会传感器网络分层结构的消息传输过程,定义阶段贡献度反映Ferry节点在消息传输过程中的贡献程度,定义区域贡献度反映Ferry节点对区域的贡献程度.在此基础上,以Ferry节点在网络中的综合贡献度作为判断关键节点的依据,提出基于多属性决策中理想点法(technique for order preference by similarity to ideal solution, TOPSIS)的关键节点预测方法.实验结果表明:采用改进TOPSIS算法能够获得更高的预测精度;搭建了实验床以进一步验证提出的预测方法,结果表明,采用改进TOPSIS算法的预测精度更高.
机会传感器网络;关键节点;区域贡献度;阶段贡献度;多属性决策
机会传感器网络(opportunistic sensor networks, OSNs)是一种利用节点移动带来的相遇机会实现通信的自组织网络,具有移动自组织网络(mobile ad hoc network, MANET)和延迟容忍网络(delay tolerant network, DTN)的特点[1],常被应用于野生动物追踪[2]、森林环境监测[3]以及智能交通[4]等方面,网络中某些节点的损坏可能导致整个网络运行不正常,甚至瘫痪,这种节点被称为关键节点.如能提前获知或预测网络的关键节点,便可根据关键节点的相关信息对网络进行优化,并尽可能地消除关键节点,以增强网络的健壮性;网络运行过程中,通过重点监视关键节点的状态、及时维护关键节点,以确保网络正常运行;一旦网络出现瘫痪,能够第一时间排查关键节点是否正常,可减少网络维护的时间和成本.本文研究OSNs的关键节点预测方法.
目前,主要有基于准则[5-6]、基于参数[7]和基于节点重要度[8-9]的关键节点预测方法.传统网络中关键节点的预测方法不再适用于机会传感器网络.本文针对OSNs消息传输时延高、网络拓扑变化频繁的特点,探索其关键节点的预测方法,为OSNs的实际应用提供支撑.
通过分析OSNs中区域节点与Sink节点之间的消息传输过程,以Ferry节点在该过程中的贡献衡量Ferry节点的重要程度,主要工作如下:1)将OSNs抽象成多区域机会传感器网络(multi-region opportunistic sensor networks, MOSNs);2)分析OSNs的拓扑特性,定义关键节点及割点;3)分析 OSNs的分层结构,将其消息传输过程分为3个阶段,定义Ferry节点的阶段贡献度及区域贡献度;4)提出基于改进多属性决策中理想点法(technique for order preference by similarity to ideal solution, TOPSIS)的OSNs关键节点预测方法;5)通过仿真实验和实验床实验验证本文提出的方法.
1 相关研究
国内外学者对网络割点(关键节点)的判定[5,10-12]、节点重要度的评估[13-15]、多属性决策理论在无线传感器网络中的应用[16-17]进行了研究.
文献[5]将覆盖网络中的所有非叶子节点视为候选割点,每一个候选割点都可发起主动探测命令,如果某候选割点有2个或2个以上的邻居之间不存在回路,则认定该疑似割点为实际割点;文献[11]针对引起耦合网络级联失效的节点,提出Max-Cas算法,采用最大连通分支的节点数鉴别关键节点;文献[12]利用前一时刻的关键节点集更新动态网络的关键节点,达到自适应探测关键节点的目的,针对动态网络,提出无需重复计算的关键节点自适应检测算法;文献[6]提出适用于大规模ad hoc网络的分布式拓扑分割探测算法(distributed partition detection protocol, DPDP),若网络中节点的邻节点度N和基本回路度M满足N-M≥2,则判定该节点为割点.
文献[18]指出加权网络中,任意2个节点对之间最重要的节点是移除后使这2个节点间的最短距离增加最多的那个节点;文献[19]比较通信网络中生成树的数目评价任意数目的2组节点的重要程度;文献[20]考虑节点自身属性及其m阶邻居节点的属性,提出复杂网络的节点重要度评价方法;文献[8]利用领域“结构洞”判别社会网络的最具影响力节点,即关键节点;文献[7]综合考虑节点度、接近度[21]、介数[22]、等价拓扑结构、邻居列表的影响,评估节点在复杂网络中的重要程度;文献[9]针对节点删除法存在的不足,定义节点效率和节点重要度评价矩阵,利用重要度评价矩阵确定复杂网络的关键节点;文献[23]提出以节点“移除”导致的网络能耗值为衡量基准,并考虑节点剩余生命期,采用节点删除法评价节点在无线传感器网络中的重要程度.
文献[16]提出基于传感器节点信誉度集对分析的安全数据进行融合,并采用多属性决策方法选择转发下一跳数据的节点;文献[17]针对无线传感器网络易出现数据流量集中于少数路径的现象,提出基于多属性决策的能量平衡路由策略MADMR(multiple attribute decision making routing).
本文参考文献[6],考虑OSNs的传输特点,定义OSNs的关键节点及割点,定义区域贡献度反映区域对Ferry节点的依赖程度,采用多属性决策(multiple attribute decision making, MADM)方法预测OSNs的关键节点.
2 场景模型及定义
根据OSNs分层结构的特点,分析OSNs中关键节点的特点,定义OSNs关键节点、区域贡献度.
2.1 OSNs场景模型
本文研究场景如图1[24]所示,区域内感知节点发送消息至移动节点,移动节点通过1次或多次转发将消息发送至Sink节点.
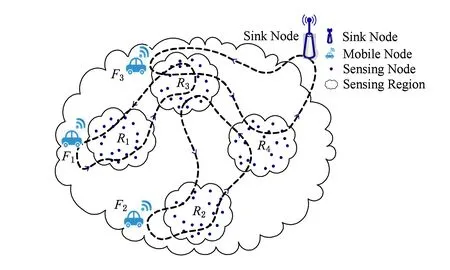
Fig. 1 MOSNs scenario图1 MOSNs场景
将一个区域抽象成一个“超级节点”,称为区域节点,得到MOSNs模型,如图2所示,R1,R2,R3,R4为区域节点,F1,F2,F3为Ferry节点.
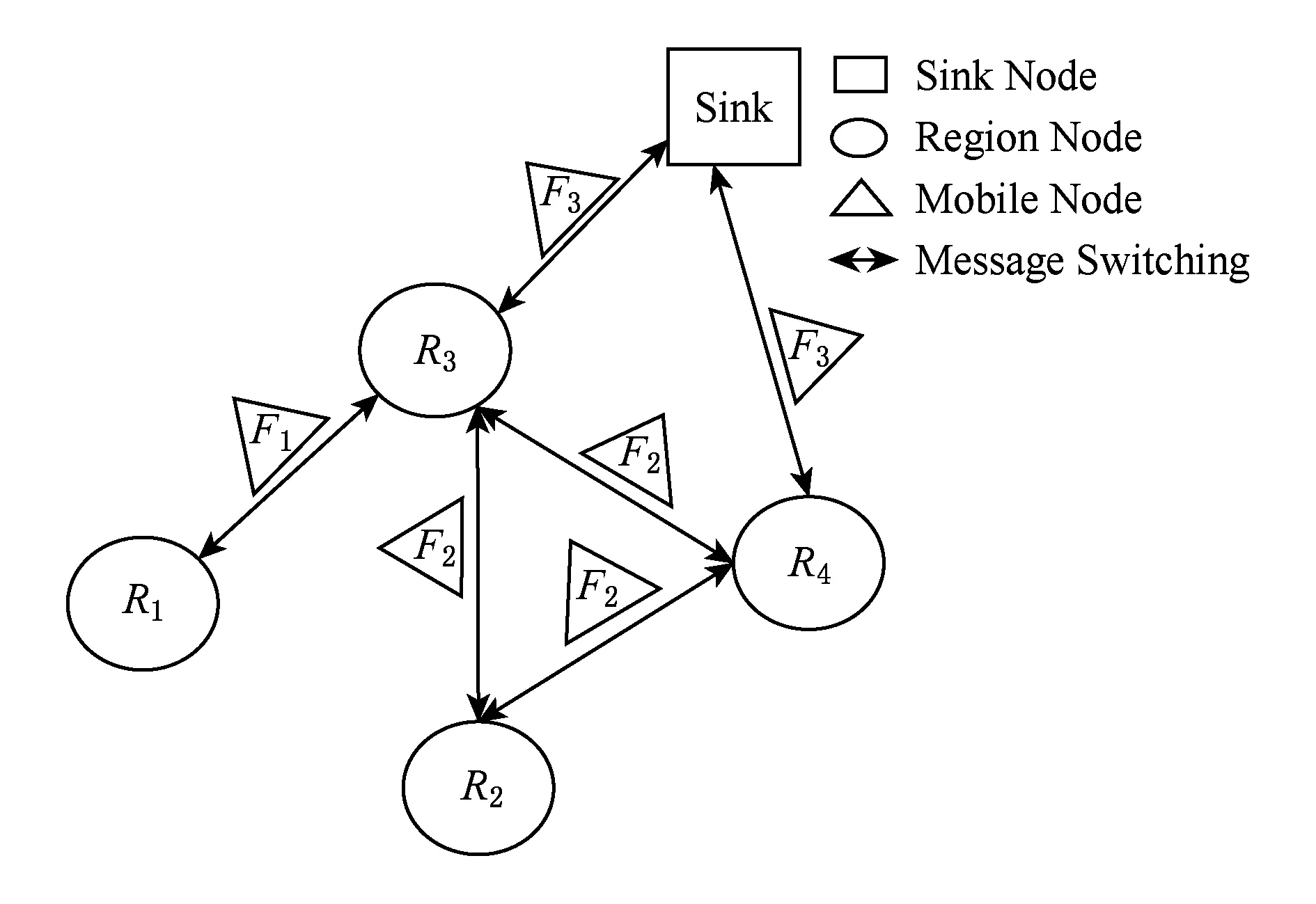
Fig. 2 MOSNs model图2 MOSNs模型
MOSNs由3类节点构成:Sink节点、Ferry节点和区域节点.区域节点负责感知周围物理世界,Sink节点负责汇聚网络消息,区域节点和Sink节点固定不动,相互之间不连通;Ferry节点负责转发消息,以随机游走或按一定规律在区域节点和Sink间移动,通过“存储—携带—转发”方式建立区域节点与Sink节点之间的通信.根据节点功能的不同,将整个网络划分为3层,如图3[25]所示.
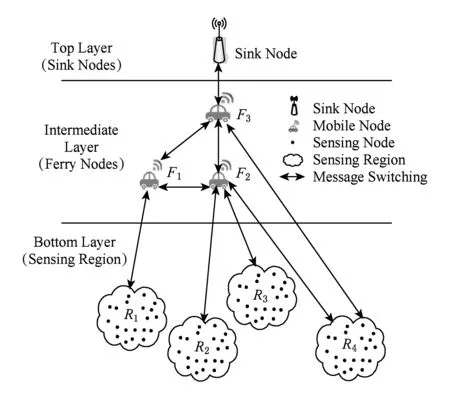
Fig. 3 MOSNs hierarchical structure图3 MOSNs的分层结构
2.2 MOSNs的关键节点
关键节点的概念来自图论,目前仍没有统一的定义.本文针对MOSNs的特点,以网络分裂概率为衡量标准,定义关键节点.
定义1. 关键节点.设G表示MOSNs,若G中某节点F移除后网络产生分裂的可能性最大,则称F为G的关键节点.
定义2. 割点.设G表示MOSNs,若移除某节点C后网络G产生分裂,则称C为网络G的割点.
由定义1、定义2得到推论1、推论2.
推论1. MOSNs的割点一定是关键节点.
证明. 由定义2可知,移除MOSNs的割点后,网络一定产生分裂.即移除MOSNs的割点后,网络产生分裂的概率为100%,故MOSNs的割点一定是关键节点.
证毕.
与传统无线传感器网络不同,MOSNs中Ferry节点的位置运动变化,其拓扑随之变化,即MOSNs处于间歇性连通状态,只要该间歇时间间隔在实际应用可容忍的范围内,便可认为整个网络是连通的.如果由于部分节点损毁、丢失或Ferry节点提供的通信机会不够频繁,使得网络的间歇时间间隔大于最大容忍值,便认为MOSNs不连通,也就是说,MOSNs结构出现了分裂,这些导致MOSNs产生分裂的节点就是关键节点.由上述分析可知,MOSNs的Ferry节点最有可能成为关键节点,但是,哪些Ferry节点是MOSNs的关键节点?这就是本文需要解决的问题.
为便于研究,本文进行如下假设:
1) 将每个区域抽象成一个“超级节点”,称区域节点;
2) 设Ferry节点的内存足够存储其经过区域时收集的全部消息;
3) MOSNs中区域节点、Ferry节点及Sink节点均有唯一的标识;
4) MOSNs已具备时钟同步机制.
2.3 阶段贡献度
Ferry节点是MOSNs的消息传输媒介,对整个网络至关重要,部分Ferry节点可能是关键节点.通过分析MOSNs的路由机制和分层结构,不难发现,感知消息从产生到最终投递到Sink的过程,可分为3个阶段:消息投递阶段、消息转发阶段和消息到达阶段,如图4所示:
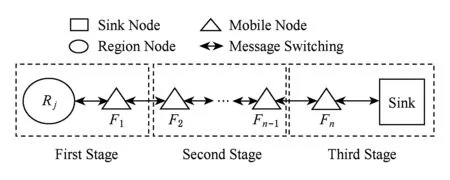
Fig. 4 MOSNs message transmission process图4 MOSNs消息传播过程
1) 消息投递阶段.Ferry节点将感知消息带离区域.
2) 消息转发阶段.消息在Ferry节点间转发.
3) 消息到达阶段.消息被Ferry节点投递至Sink.
定义3. 第1阶段贡献度(first stage contribu-tion, FSC).设时间T内,Sink收到Mj条来自区域Rj的消息,如果Ferry节点Fi在消息投递阶段共接收ni j(ni j≤Mj)条来自区域Rj的消息,则Fi对区域Rj的第1阶段贡献度为ni jMj,记为FSC(Fi,Rj).
定义4. 第2阶段贡献度(second stage contri-bution, SSC). 设时间T内,Sink收到Mj条来自区域Rj的消息,如果Ferry节点Fi在消息转发阶段共转发mi j(mi j≤Mj)条来自区域Rj的消息,则Fi对区域Rj的第2阶段贡献度为mi jMj,记为SSC(Fi,Rj).
定义5. 第3阶段贡献度(third stage contribu-tion, TSC). 设时间T内,Sink收到Mj条来自区域Rj的消息,如果Ferry节点Fi在消息到达阶段共投递ki j(ki j≤Mj)条来自区域Rj的消息至Sink节点,且Fi对区域Rj的第3阶段贡献度为ki jMj,记为TSC(Fi,Rj).
显然,FSC反映了Ferry节点在消息投递阶段对消息传输的贡献程度;SSC反映了Ferry节点在消息转发阶段对消息传输的贡献程度;TSC反映了Ferry节点在消息到达阶段对消息传输的贡献程度.
2.4 区域贡献度
定义6. 区域贡献度(region contribution, RC). 时间T内,若Ferry节点Fi对区域Rj的第1阶段、第2阶段、第3阶段的贡献度分别为FSC(Fi,Rj),SSC(Fi,Rj),TSC(Fi,Rj),则称RC(Fi,Rj)=αFSC(Fi,Rj)+βSSC(Fi,Rj) +γTSC(Fi,Rj)为Fi对区域Rj的区域贡献度,记为RC(Fi,Rj),其中,α+β+γ=1,0<α,β,γ<1.
本文采用层次分析法[26-28](analytic hierarchy process, AHP),使用层次分析法软件yaahp(yet another AHP)得到α=0.681 3,β=0.068 8,γ=0.249 9.
区域贡献度RC反映Ferry节点对区域贡献程度的同时,也反映了区域对Ferry节点的依赖程度,即Ferry节点对区域的RC越大,区域对Ferry节点的依赖程度越高,移除此节点后,区域从网络中分裂出去的可能性越大,则该节点为关键节点的可能性就越大.若Ferry节点Fi对某区域Rj的贡献值为1,则表明Rj完全依赖于Fi,即移除Fi后,Rj从整网中分离.由此,可以得到推论2.
推论2. 区域贡献度为1的Ferry节点是MOSNs的割点.
由推论1、推论2得到推论3.
推论3. 区域贡献度为1的Ferry节点是MOSNs的关键节点.
3 预测MOSNs的关键节点
MOSNs关键节点的预测步骤如下:
1) 根据推论2判定网络中是否存在割点.计算每个Ferry节点对各区域的贡献度,判断是否存在对某区域贡献度为1的Ferry节点.若存在,则该割点为网络的关键节点,预测结束,否则进入步骤2.
2) 采用MADM方法找出导致网络分裂可能性最大的节点,即为关键节点.用区域贡献度表征区域对Ferry节点的依赖程度,故Ferry节点的区域贡献度越大,其导致网络分割的可能性越大,因此本文采用改进TOPSIS方法将MOSNs中每个Ferry节点看作一个待评价方案,将Ferry节点对每个区域节点的贡献度看作方案的属性,对Ferry节点的区域贡献度进行评价.
3.1 预测算法描述
MOSNs网络结构动态变化,用一个时间长度ΔT时间计算的结果作为最后的预测结果是不准确的,将每一个ΔT预测的结果称为疑似关键节点.选取N×ΔT作为预测时间长度,得到N个疑似关键节点,统计每个Ferry节点被判定为疑似关键节点的次数.
设MOSNs中有n个Ferry节点(方案)和m个区域节点(属性),对决策矩阵X=(xi j)n×m归一化,得到规范化决策矩阵Y=(yi j)n×m且:
(1)
其中,xi j为第i个Ferry节点对第j个区域节点的区域贡献度,i=1,2,…,n,j=1,2,…,m.
确定正理想方案Y+和负理想方案Y-,以及各Ferry节点方案与Y+,Y-的距离D+,D-:
(2)
(3)
(4)

(5)
其中,正理想方案为
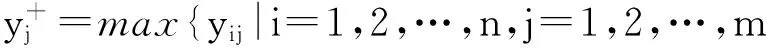
(6)
负理想方案为
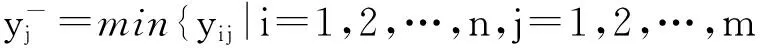
(7)
根据指标权重对欧氏距离计算公式进行改进:
(8)
(9)
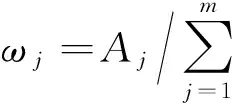
计算各Ferry节点与正理想解和负理想解的灰色关联度:
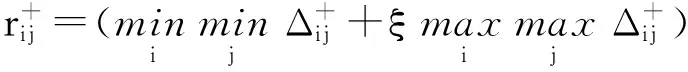
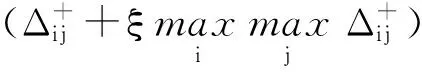
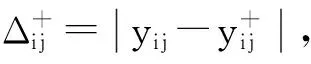
(10)
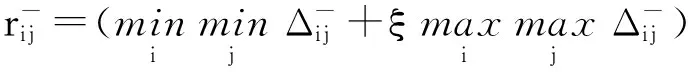
(11)
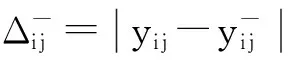
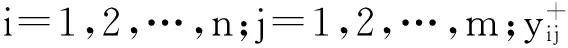
(12)
(13)
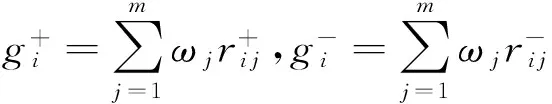
对灰色关联度和距离进行无量纲转化:
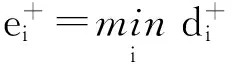
(14)
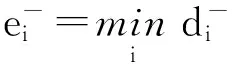
(15)
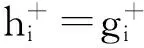
(16)
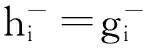
(17)
其中,i=1,2,…,n.
(18)
(19)
其中,i=1,2,…,n;α为偏好系数,取经验值0.5.则各Ferry节点的相对贴近度为
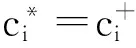
(20)
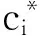
由于网络中可能存在多个割点,故预测的结果可能是多个关键节点.这就需要计算某个Ferry节点为关键节点的概率.
设MOSNs中有d个Ferry节点且每个Ferry节点都可能导致网络产生分割,若Ferry节点Fi被判定为疑似关键节点q次,则Fi为关键节点的概率为
P(Fi)=
(21)
计算出P(Fi)的最大值,记为max(P(Fi)),此时对应Ferry节点记为Fk,k∈{1,2,…,d},即为关键节点.
3.2 算法流程
算法1. 基于灰关联度的改进TOPSIS算法.
输入:多属性决策矩阵X=(xi j)n×m;
输出:节点Fi的出现概率P(Fi).
Step1. 基于时间长度ΔT,对数据进行采样分析,构建决策矩阵X=(xi j)n×m,并依据式(1)进行归一化,得到规范化矩阵Y=(yi j)n×m;
Step2. 根据式(2)~(5)分别计算决策的正理想方案Y+和负理想方案Y-,以及各节点方案与Y+,Y-的距离D+,D-;
Step3. 依据式(10)~(11)计算正理想方案和负理想方案的灰关联度G+,G-;
Step4. 基于式(14)~(17)分别对距离和灰关联度进行无量纲转化;
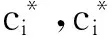
Step6. 重复Step1~Step5共N次,统计每个Ferry节点被判定为疑似关键节点的次数;
Step7. 根据式(21)计算每个节点的出现概率P(Fi),并进行排序,从中选出最大概率值所对应的Ferry节点即为关键节点.
4 实验设计与分析
4.1 实验场景与相关参数
采用芬兰赫尔辛基科技大学开发的ONE(opportunistic networking environment)进行仿真实验,主要参数如表1所示,4种典型场景下区域节点数和各区域内感知节点数如表2所示.
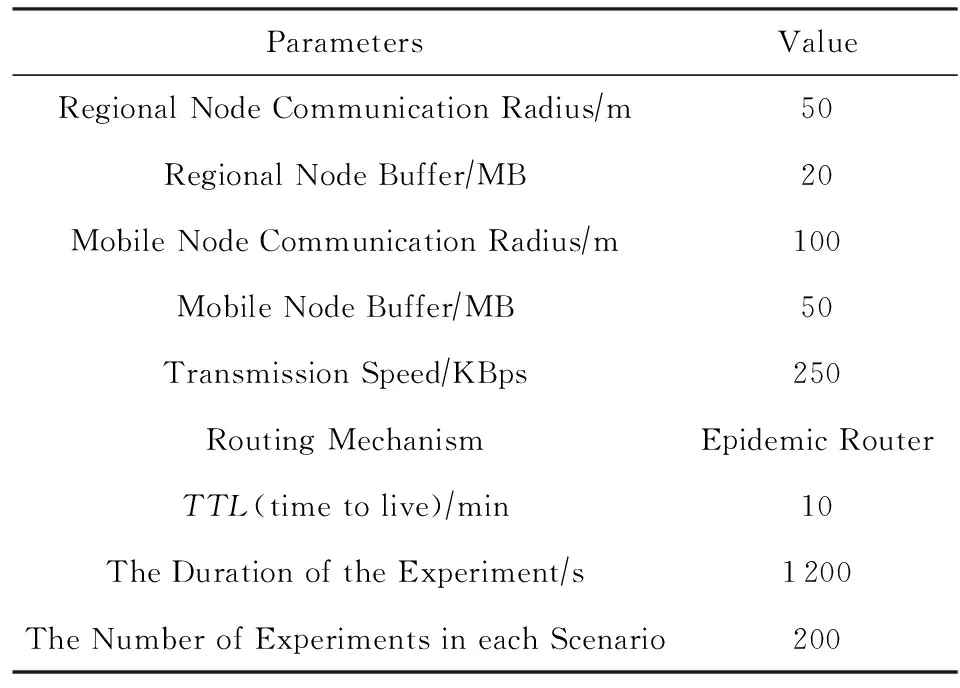
Table 1 Parameters of Simulation Experiment
如图5所示,场景1不存在割点.Ferry节点fb,fc,fd在区域节点ra,rb,rc间移动,不能与Sink节点直接通信,Ferry节点fa,fe,fg为区域节点ra与Sink提供通信机会.ra与Sink间的绝大部分通信机会由fa提供,ra与Sink间极少部分的通信机会由fe,fg提供.因此,fa为场景1的关键节点.
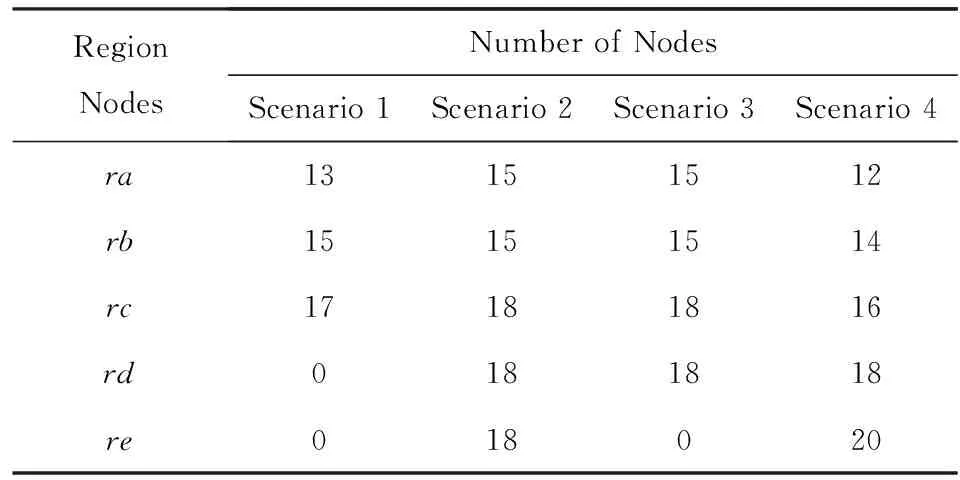
Table 2 The Number of Region Nodes in Four Scenarios
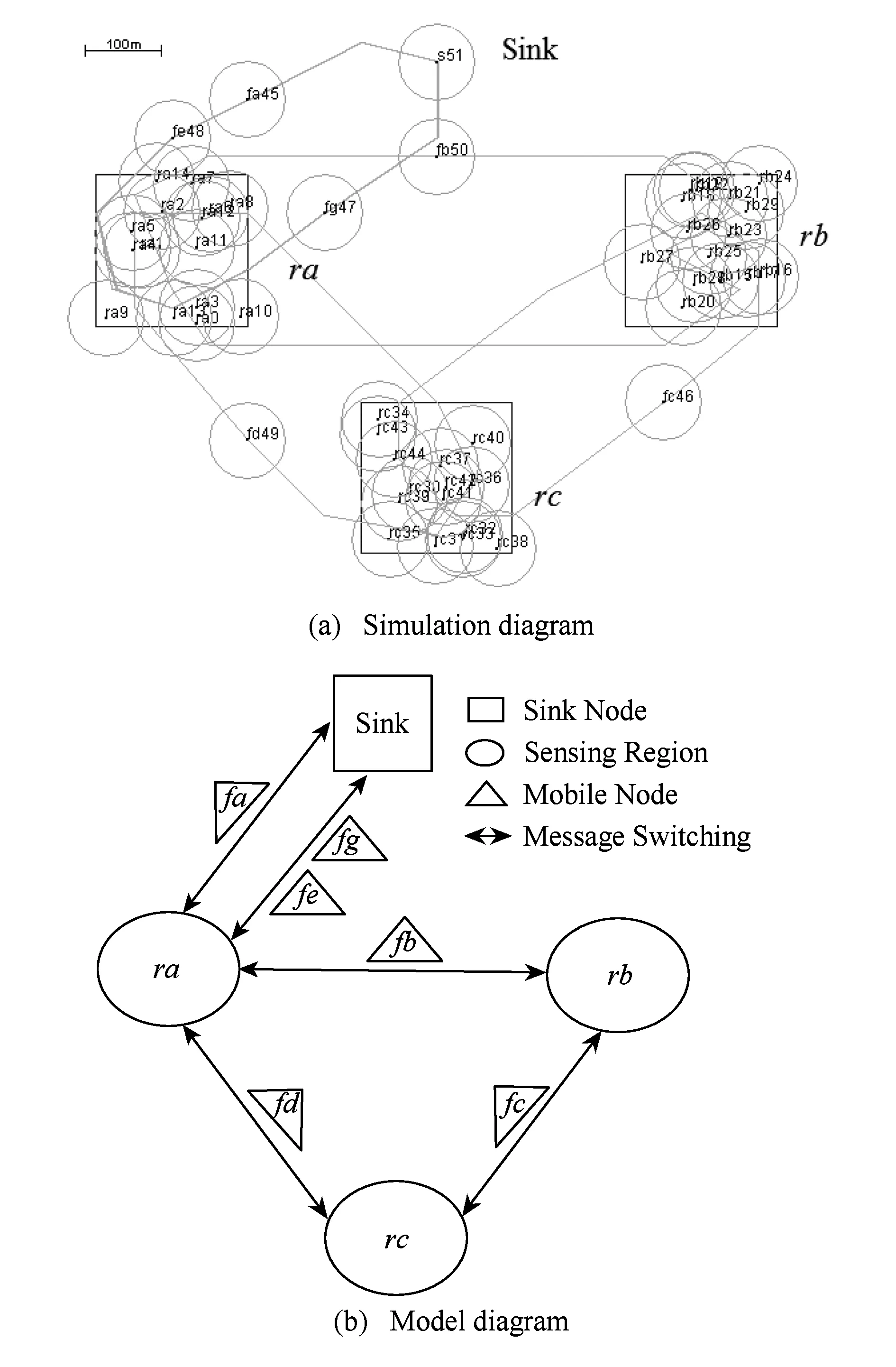
Fig. 5 Scenario 1图5 场景1
如图6所示,场景2的关键节点为fd.如果移动节点fd丢失或失效,区域节点rc,rd,re无法将消息传递到Sink节点,网络产生分割,故fd既是网络的割点,也是网络的关键节点.
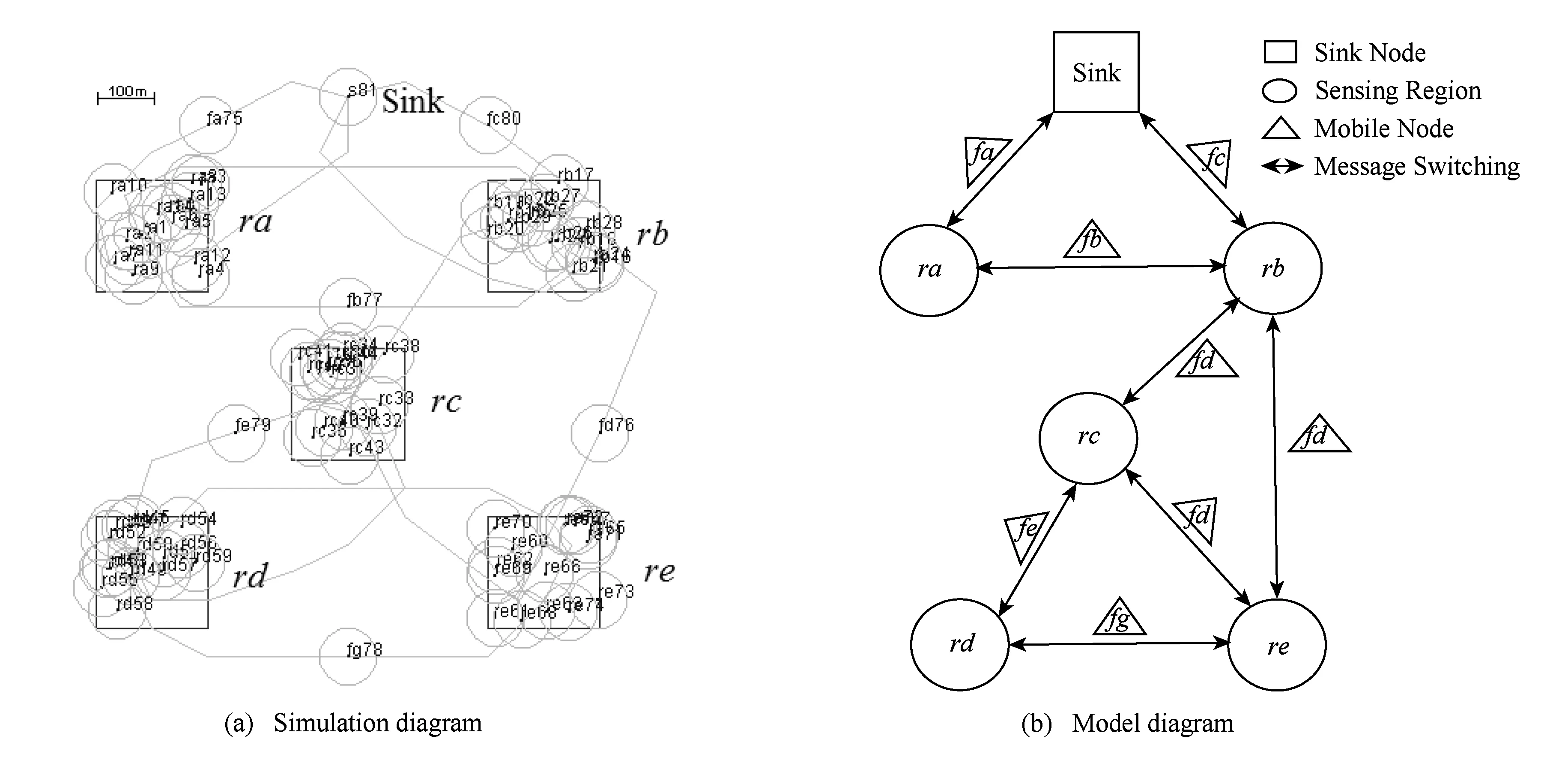
Fig. 6 Scenario 2图6 场景2
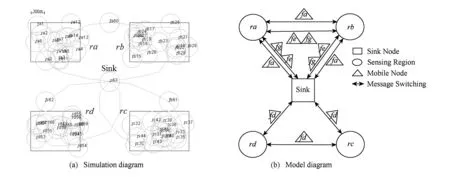
Fig. 7 Scenario 3图7 场景3
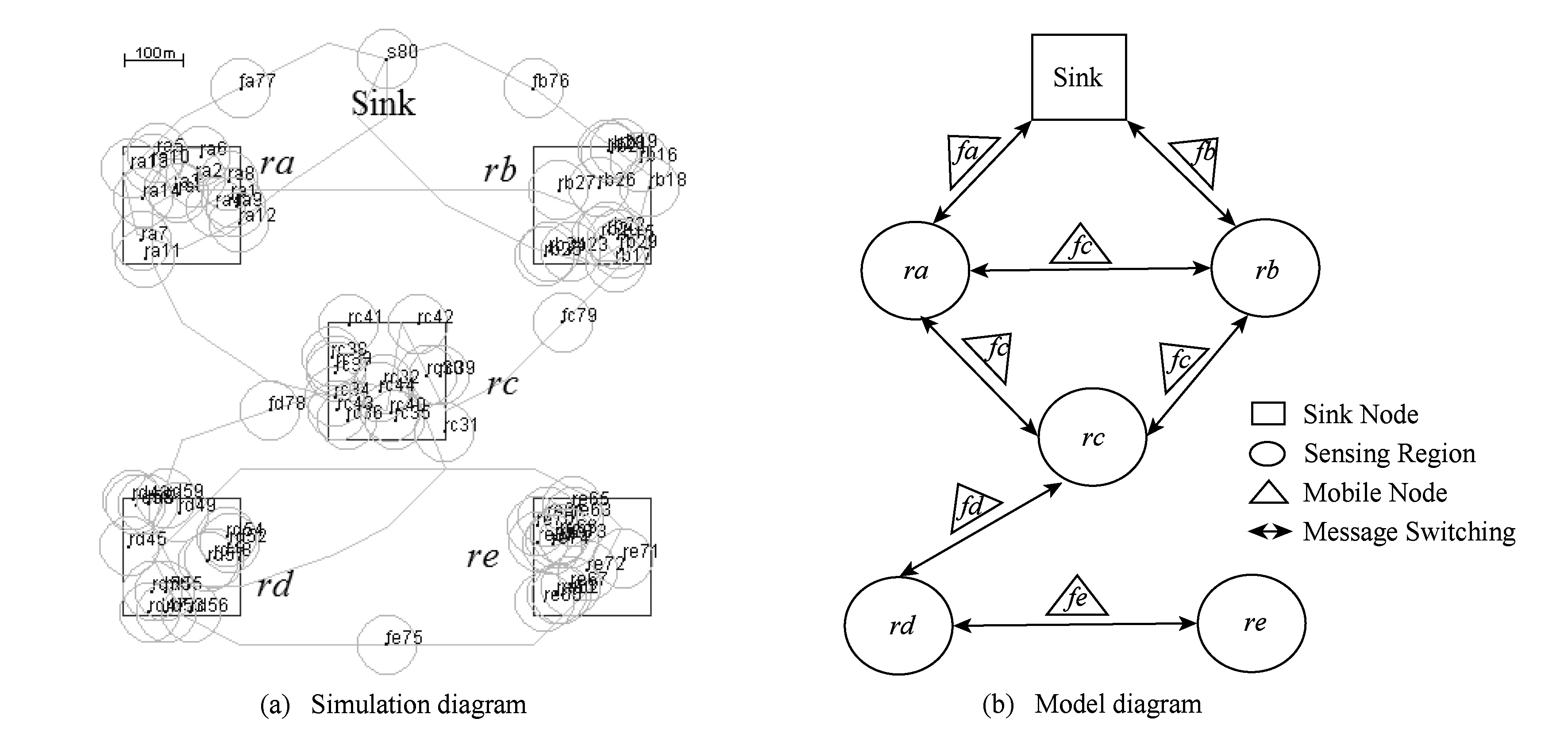
Fig. 8 Scenario 4图8 场景4
如图7所示,场景3不存在割点.区域节点ra,rb与Sink节点间绝大部分的通信机会由移动节点fa提供,极少的通信机会由移动节点fe,fg提供.可见,fa为场景3的关键节点.
如图8所示,场景4的关键节点为fd,fe.如果移动节点fd丢失或失效会导致区域节点rd,re从网络分裂,移动节点fe失效会导致区域节点re从网络分离.深入分析场景4,发现移动节点fc也是该网络的1个割点,移动节点fa,fb,fc使区域节点ra,rb与Sink节点形成两两相互连通的稳定状态,移动节点fc又连通着区域节点ra,rb,rc,若移动节点fc丢失或失效,则区域节点rc,rd,re均无法与Sink节点连通.所以,场景4的关键节点为移动节点fc,fd,fe.
4.2 实验结果与分析
对上述4种场景进行了大量模拟实验,采用TOPSIS算法和改进TOPSIS算法对实验数据进行关键节点预测,预测结果如图9~12所示:
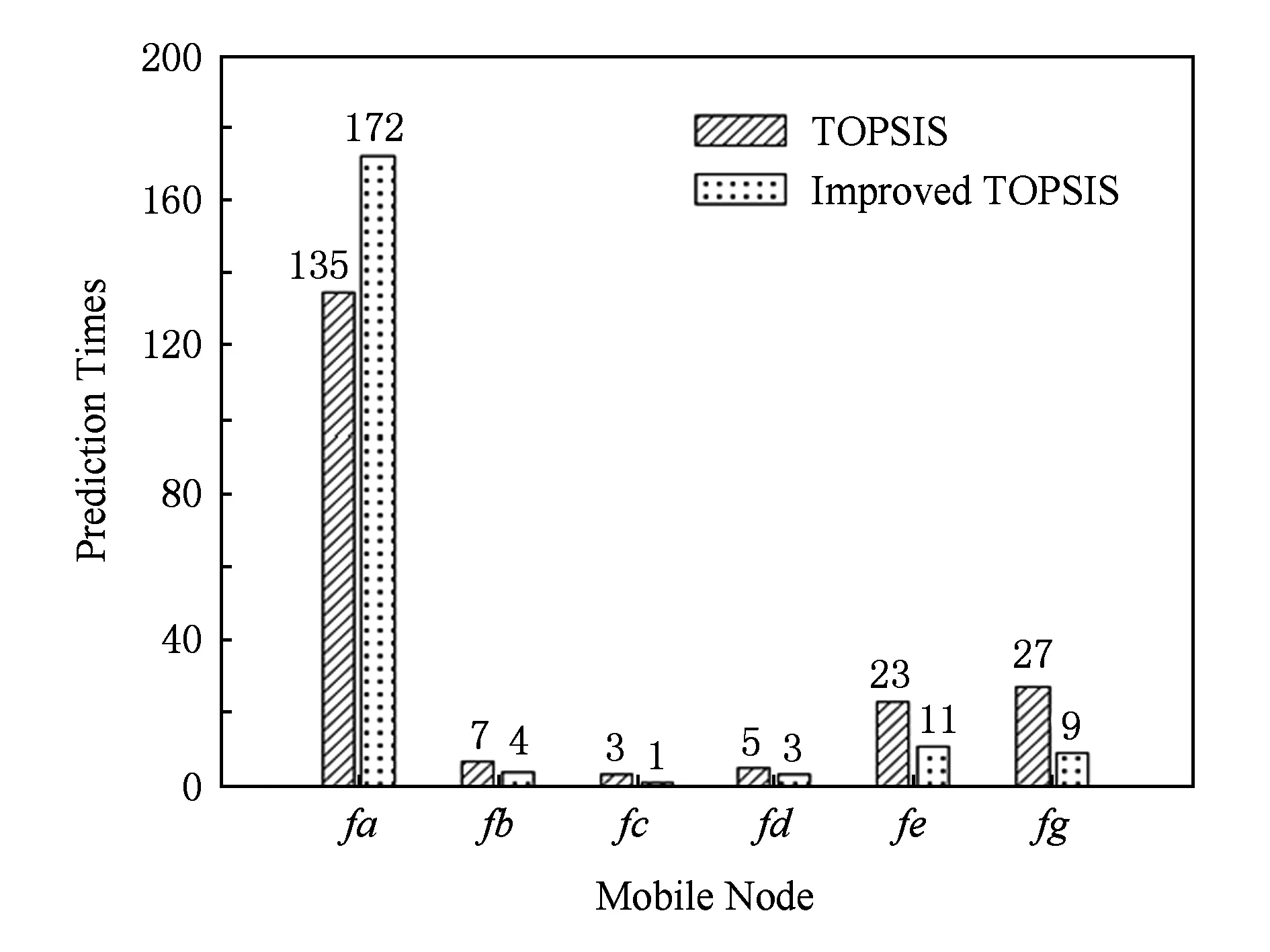
Fig. 9 Predicted results of scenario 1图9 场景1的预测结果
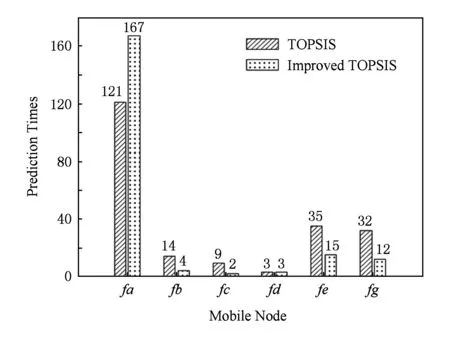
Fig. 11 Predicted results of scenario 3图11 场景3的预测结果
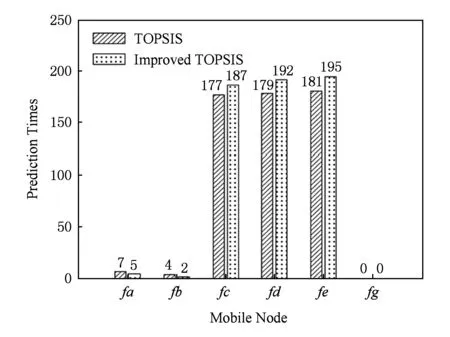
Fig. 12 Predicted results of scenario 4图12 场景4的预测结果
如图9所示,场景1中移动节点fa被预测为关键节点的次数最多,与前述分析结果一致,说明采用本文预测算法的合理性;如图10所示,场景2中被预测为关键节点次数最多的是移动节点fd;如图11所示,场景3中被预测为关键节点次数最多的是移动节点fa,均与前述分析一致;如图12所示的场景4中,移动节点fc,fd,fe多次被预测为关键节点,且三者的次数之和远远大于总实验次数200,这是因为场景4中存在3个割点,因此每次预测的关键节点可能不唯一,Ferry节点fc,fd,fe均为该场景下的关键节点.
由图9~12可得采用TOPSIS算法与改进TOPSIS算法预测关键节点的精度对比情况,如图13所示.场景2与场景4存在割点,2种算法的预测精度接近;场景1与场景3不存在割点,采用TOPSIS算法的预测精度在60%~70%范围内,而采用改进TOPSIS算法的预测精度达到80%~90%.可见,当MOSNs存在割点时,2种预测方法均较为准确;当MOSNs不存在割点时,采用改进TOPSIS算法的预测精度更高.
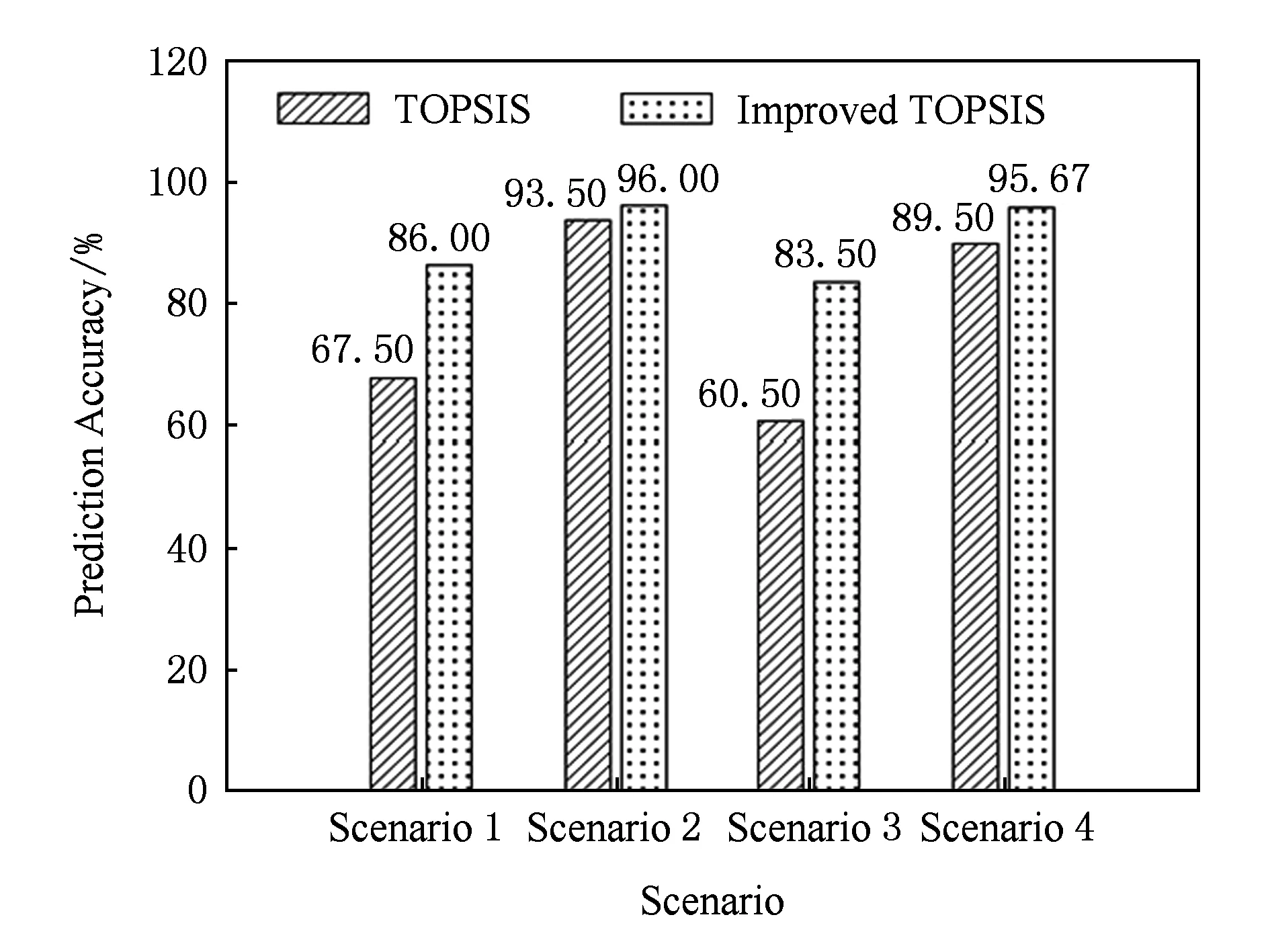
Fig. 13 The accuracy comparison chart of two measures图13 2种方法的预测精度对比图
4.3 实验床实验
搭建实验床如图14所示,在寻迹小车上捆绑美国Crossbow公司的TelosB节点,模拟MOSNs中移动节点寻迹移动,利用黑线规划4条小车的移动轨迹.TelosB节点遵循IEEE802.15.4协议,通信范围约100 m,在实验中,将节点功率调至最低,并去掉天线,使节点的通信范围为10~20 cm,以满足图1场景.
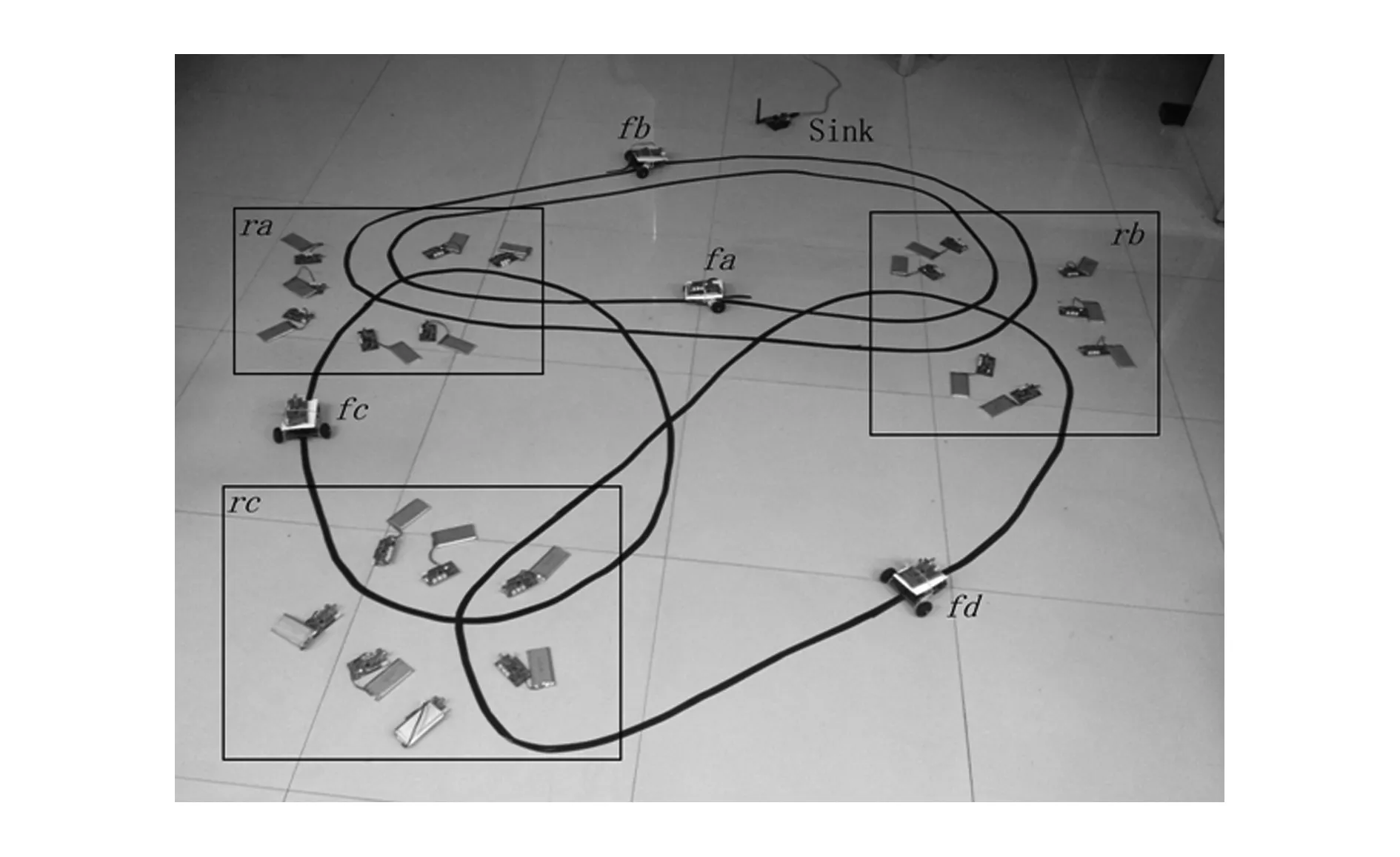
Fig. 14 The test bed图14 实验床
设置了3个区域节点,每个区域节点内放置若干个感知节点,区域节点ra,rb与Sink节点间设置了2辆小车,为了模拟小车fa为区域ra,rb提供绝大部分通信机会,小车fb为区域ra,rb提供较少的通信机会,设置轨迹半径较小的小车fa速度较快,轨迹半径较大的小车fb速度较慢,那么该场景下,小车fa是关键节点.
利用TOPSIS算法与改进TOPSIS算法分别对实验数据进行分析,100次实验的预测结果如图15所示.100次预测中,采用改进TOPSIS算法预测小车fa为关键节点的次数为73,预测精度为73%,采用 TOPSIS算法的预测精度为55%,显然改进TOPSIS算法具有更高的预测精度.
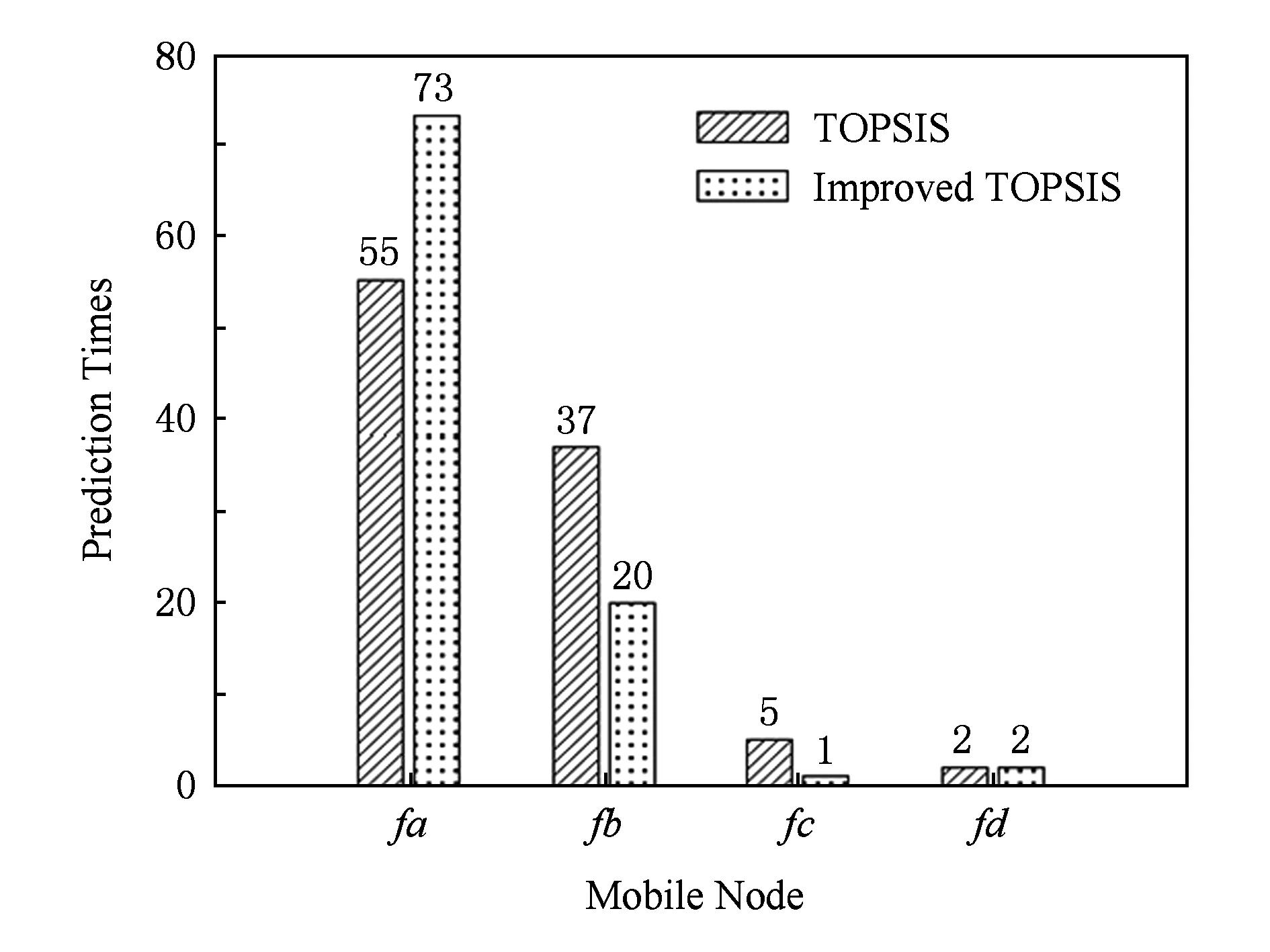
Fig. 15 The predicted results of real scenario图15 真实场景预测结果
5 结束语
本文分析了OSNs消息传输的特点,针对典型OSNs——多区域机会传感器网络MOSNs模型,定义了割点和关键节点,将MOSNs关键节点预测问题转化为评估Ferry节点区域贡献度的问题,采用改进TOPSIS算法预测关键节点.仿真实验和实验床实验均说明本文的定义是合理的,通过评估Ferry节点区域贡献度预测MOSNs关键节点是可行的,采用改进TOPSIS算法具有更高的预测精度.
[1]Xiong Yongping, Sun Limin, Niu Jianwei, et al. Opportunistic networks[J]. Journal of Software, 2009, 20(1): 124-137 (in Chinese)(熊永平, 孙利民, 牛建伟, 等. 机会网络[J]. 软件学报, 2009, 20(1): 124-137)
[2]Hull B, Bychkovsky V, Zhang Yang, et al. CarTel: A distributed mobile sensor computing system[C]Proc of ACM SenSys’06. New York: ACM, 2006: 125-138
[3]Wang Yu, Wu Hongyi. DFT-MSN: The delayfault-tolerant mobile sensor network for pervasive information gathering[C]Proc of INFOCOM’06. Piscataway, NJ: IEEE, 2006: 1021-1034
[4]Juang P, Oki H, Wang Yong, et al. Energy-efficient computing for wildlife tracking: Design tradeoffs and early experiences with ZebraNet[J]. ACM SIGPLAN Notices, 2002, 37(10): 96-107
[5]Liu Xiaomei, Xiao Li, Kreling A, et al. Optimizing overlay topology by reducing cut vertices[C]Proc of ACM NOSSDAV’06. New York: ACM, 2006
[6]Li Jiandong, Tian Ye, Sheng Min, et al. Partition detection for large scale ad hoc networks[J]. Journal on Communications, 2008, 29(9): 54-61 (in Chinese)(李建东, 田野, 盛敏, 等. 大规模ad hoc网络拓扑分割探测研究[J]. 通信学报, 2008, 29(9): 54-61)
[7]Hu Jun, Wang Bing, Lee Deyi. Evaluating node importance with multi-criteria[C]Proc of IEEEACM GreenCom-CPSCom. Piscataway, NJ: IEEE, 2010: 792-797
[8]Su Xiaoping, Song Yurong. Leveraging neighborhood “structural holes” to identifying key spreaders in social networks[J]. Acta Physica Sinica, 2015, 64(2): 1-11 (in Chinese)(苏晓萍, 宋玉蓉. 利用邻域“结构洞”寻找社会网络中最具影响力节点[J]. 物理学报, 2015, 64(2): 1-11)
[9]Zhou Xuan, Zhang Fengming, Li Kewu, et al. Finding vital node by node importance evaluation matrix in complex networks[J]. Acta Physica Sinica, 2012, 61(5): 1-7 (in Chinese)(周漩, 张凤鸣, 李克武, 等. 利用重要度评价矩阵确定复杂网络关键节点[J]. 物理学报, 2012, 61(5): 1-7)
[10]Xiong Shuguang, Li Jianzhong. An efficient algorithm for cut vertex detection in wireless sensor networks[C]Proc of IEEE ICDCS’10. Piscataway, NJ: IEEE, 2010: 368-377
[11]Nguyen D T, Shen Y, Thai M T. Detecting critical nodes in interdependent power networks for vulnerability assessment[J]. IEEE Trans on Smart Grid, 2013, 4(1): 151-159
[12]Shen Yilin, Nguyen N P, Xuan Ying, et al. On the discovery of critical links and nodes for assessing network vulnerability[J]. IEEEACM Trans on Networking, 2013, 21(3): 963-973
[13]Nacher J C, Akutsu T. Analysis on critical nodes in controlling complex networks using dominating sets[C]Proc of IEEE SITIS’13. Piscataway, NJ: IEEE, 2013: 649-654
[14]Du Guiping, He Lidan, Fang Junxiang. The component importance evaluation of power converter based on complex network[C]Proc of IEEE PEAC’14. Piscataway, NJ: IEEE, 2014: 988-992
[15]Lin Jian, Dai Fei, Li Baichao, et al. Electromagnetic compatibility supernetwork modeling and node importance evaluation[C]Proc of the 5th Int Conf on Intelligent Human-Machine Systems and Cybernetics. Piscataway, NJ: IEEE, 2013: 306-310
[16]Ma Shouming, Wang Ruchuan, Ye Ning. Secure data aggregation algorithm based on reputation set pair analysis in wireless sensor networks[J]. Journal of Computer Research and Development, 2011, 48(9): 1652-1658 (in Chinese)(马守明, 王汝传, 叶宁. 基于信誉度集对分析的WSN安全数据融合[J]. 计算机研究与发展, 2011, 48(9): 1652-1658)
[17]Zeng Jia, Mu Chundi, Li Shu. Multiple attribute decision making routing in wireless sensor networks[J]. Journal of System Simulation, 2009,21(3): 878-881 (in Chinese)(曾加, 慕春棣, 李戍. 基于多属性决策的无线传感器网络路由算法[J]. 系统仿真学报, 2009, 21(3): 878-881)
[18]Corley H W, Sha D Y. Most vital links and nodes in weighted networks[J]. Operations Research Letters, 1982, 1(4): 157-160
[19]Chen Yong, Hu Aiqun, Hu Xiao. Evaluation method for node importance in communication networks[J]. Journal on Communications, 2004, 25(8): 129-134 (in Chinese)(陈勇, 胡爱群, 胡啸. 通信网中节点重要性的评价方法[J]. 通信学报, 2004, 25(8): 129-134)
[20]Zhang Xiping, Li Yongshu, Liu Gang, et al. Evaluation method of importance for nodes in complex networks based on importance contribution[J]. Complex Systems and Complexity Science, 2014, 11(3): 26-32 (in Chinese)(张喜平, 李永树, 刘刚, 等. 节点重要度贡献的复杂网络节点重要度评估方法[J]. 复杂系统与复杂性科学, 2014, 11(3): 26-32)
[21]Sabidussi G. The centrality index of a graph[J]. Psychometrika, 1966, 31(4): 581-603
[22]Freeman L C. A set of measures of centrality based on betweenness[J]. Sociometry, 1977, 40(1): 35-41
[23]Liu Bin, Wang Wenji, Li Yaqian, et al. Crucial node decision algorithm based on energy in WSNs[J]. Journal of Electronics and Information Technology, 2014, 36(7): 1728-1734 (in Chinese)(刘彬, 王文吉, 李雅倩, 等. 基于能量因素的无线传感器网络关键节点判定算法[J]. 电子与信息学报, 2014, 36(7): 1728-1734)
[24]Shu Jian, Geng Xiaotian, Zeng Linxin, et al. Connectivity influencing factors and modeling for opportunistic sensor networks[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(6): 109-114 (in Chinese)(舒坚, 耿潇湉, 曾林新, 等. 机会传感网络连通度影响因素与连通度模型[J]. 北京邮电大学学报, 2015, 38(6): 109-114)
[25]Shu Jian, Guo Kai, Liu Qun, et al. Research of connectivity parameter in opportunistic sensor networks[J]. Chinese Journal of Computers, 2016, 39(5): 1067-1080 (in Chinese)(舒坚, 郭凯, 刘群, 等. 机会传感网络连通性参数研究[J]. 计算机学报, 2016, 39(5): 1067-1080)
[26]Yu Hui, Liu Zun, Li Yongjun. Key nodes in complex networks identified by multi-attribute decision-making method[J]. Acta Physica Sinica, 2013, 62(2): 46-54 (in Chinese)(于会, 刘尊, 李勇军. 基于多属性决策的复杂网络节点重要性综合评价方法[J]. 物理学报, 2013, 62(2): 46-54)
[27]Sha Letian, Fu Jianming, Chen Jing, et al. A sensitivity measurement for sensitive information processing[J]. Journal of Computer Research and Development, 2014, 51(5): 1050-1060 (in Chinese)(沙乐天, 傅建明, 陈晶, 等. 一种面向敏感信息处理的敏感度度量方法[J]. 计算机研究与发展, 2014, 51(5): 1050-1060)
[28]Wang Wenbin, Sun Qibo, Yang Fangchun. Environment-aware quantitative assessment model for service availability in MANET[J]. Journal of Computer Research and Development, 2012, 49(3): 558-564 (in Chinese)(王文彬, 孙其博, 杨放春. MANET下环境感知的服务可用性量化评估模型[J]. 计算机研究与发展, 2012, 49(3): 558-564)


Zhang Jiang, born in 1992. MSc candidate in Nanchang Hangkong University. His main research interests include opportunistic sensor networks (zhangjiangky@163.com).

Shu Jian, born in 1964. Received his MSc degree in computer networks from North-western Polytechnical University. Professor in Nanchang Hangkong University. Senior member of CCF. His main research interests include wireless sensor networks, embedded system and software engineering.

Guo Kai, born in 1990. MSc candidate in Nanchang Hangkong University. Student member of CCF. His main research interests include opportunistic sensor networks (1056692868@qq.com).

Meng Lingchong, born in 1991. MSc candidate in Nanchang Hangkong University. His main research interests include opportunistic sensor networks (282733193@qq.com).
Multiple Attribute Decision Making-Based Prediction Approach of Critical Node for Opportunistic Sensor Networks
Liu Linlan1, Zhang Jiang1, Shu Jian2, Guo Kai1, and Meng Lingchong1
1(SchoolofInformationEngineering,NanchangHangkongUniversity,Nanchang330063)2(SchoolofSoftware,NanchangHangkongUniversity,Nanchang330063)
If critical nodes have been predicted, the network can be optimized according to the information of the critical nodes. Furthermore, maintenance time and cost of network can be dramatically reduced by checking the critical nodes at the first time when the network is crashed. Unfortunately, the existing methods of predicting critical nodes in static wireless sensor networks are not suitable for opportunistic sensor networks (OSNs). According to the characteristics of dynamic changes of network topology and high latency, for multi-region OSNs (MOSNs) with hierarchical structure, this paper analyzes the message transferring process. The stage contribution is defined to reflect the contribution of Ferry nodes in the process of message transmission, and the region contribution is defined to reflect the contribution of Ferry nodes to regions. In terms of the comprehensive contribution of Ferry nodes, the prediction method of critical nodes is proposed, which is based on multiple attribute decision making—technique for order preference by similarity to ideal solution (TOPSIS). The experimental results show that the prediction method with improved TOPSIS algorithms achieves better accuracy. Furthermore, test bed is established so as to validate the proposed method. The test bed experimental results show that the prediction method with improved TOPSIS algorithms achieves better accuracy as well.
opportunistic sensor networks (OSNs); critical node; region contribution; stage contribution; multiple attribute decision making
her BSc degree in computer application from the National University of Defence Technology. Professor in Nanchang Hangkong University. Member of CCF. Her main research interests include software engineering and distributed system.
2016-08-22;
2017-02-06
国家自然科学基金项目(61363015,61262020,61501217,61501218);江西省自然科学基金重点项目(20171ACB20018,20171BAB202009,20071BBH80022);江西省教育厅科学技术重点项目(GJJ150702); 江西省研究生创新专项资金项目(YC2015-S324,YC2016-042) This work was supported by the National Natural Science Foundation of China (61363015, 61262020, 61501217, 61501218), the Natural Science Foundation of Jiangxi Province (20171ACB20018, 20171BAB202009, 20071BBH80022), the Key Research Foundation of Education Bureau of Jiangxi Province(GJJ150702), and the Innovation Foundation for Postgraduate Student of Jiangxi Province (YC2015-S324, YC2016-042).
舒坚(shujian@nchu.edu.cn)
TP393
