动能拦截弹三维末制导律设计
2017-09-15田宏亮许晓艳
田宏亮, 许晓艳
(中国空空导弹研究院, 河南 洛阳 471009)
动能拦截弹三维末制导律设计
田宏亮, 许晓艳
(中国空空导弹研究院, 河南 洛阳 471009)
通过非线性系统反馈线性化得到动能拦截弹的精确线性模型, 根据动能拦截弹脱靶量分析结果和制导精度要求, 结合直接力控制特点, 设计了拦截弹三维末制导律。 仿真验证了所设计制导律的有效性, 满足拦截高空高速目标的技术需求。
临近空间; 高超声速; 动能拦截; 制导律; 线性化
0 引 言
高空高速飞行器极大地缩短了飞行器在防空系统攻击区内的逗留时间, 原有防空系统很难拦截。 文献[1]开展了动能拦截弹的制导控制建模与分析。 文献[2-3]针对反临反导问题开展了H∞末制导律、 最优制导律和滑模变结构制导律研究, 但没有考虑不连续直接力控制对制导精度的影响。 文献[4-8]采用适用于非线性系统的逆系统方法设计了制导律, 并考虑输入输出解耦线性化等问题, 但不能满足动能杀伤目标的制导需求。 文献[9]分析影响脱靶量的因素, 用非线性精确线性化理论求取非线性二维末制导律, 满足动能杀伤目标, 但没有把制导律推广到三维空间。 本文基于以上文献的研究结论, 结合导弹飞行力学和控制理论[10-11], 并考虑了视线角速度问题[12-13], 开展了三维末制导律设计及其仿真研究, 满足基于不可调直接力装置动能杀伤高空高速机动目标的技术需求。
1 目标拦截过程的数学描述
根据文献[9]给出的惯性坐标系oXgYgZg、 拦截器弹体坐标系oX1Y1Z1和视线坐标系oξηζ之间的关系, 设视线坐标系相对惯性坐标系的旋转角速度为ω, 则有

(1)

拦截器与目标相对矢径为ρ, 拦截器与目标的相对速度为

(2)
拦截器与目标的相对加速度为
(3)
(4)
其中,aMX1,aMY1,aMZ1是拦截器的推力产生的加速度在弹体坐标系各轴上的投影,aMX1用u11代表,aMZ1用u12代表,aMY1用u13代表;aTX1,aTY1,aTZ1是目标的机动加速度在弹体坐标系各轴上的投影, 设aTX1≈0。
2 末制导算法设计
2.1 基于反步线性化的非线性制导指令设计
状态方程(4)可简化写成

(5)
其中,
选取输出量为
(6)
然后进行精确反步线性化,Lg1h1(x)=Lg2h1(x)=Lg3h1(x)=0,Lfh1(x)=x2,Lg1Lfh1(x)=-1,Lg2Lfh1(x)=Lg3Lfh1(x)=0,Lg2h2(x)=-1/x1,Lg1h2(x)=Lg3h2(x)=0,Lg1h3(x)=Lg2h3(x)=0,Lg3h3(x)=1/x1,

坐标变换矩阵为
z=φ(x)=[φ1(x)φ2(x)φ3(x)φ4(x)]T= [h1(x)Lfh1(x)h2(x)h3(x)]T= [x1x2x3x4]T
(7)
从变换矩阵可以看出, 式(5)不需经坐标变换, 只需反馈就可进行精确线性化, 反馈矩阵为
u=M-1(x)(-b(x)+v)
(8)
其中,v=[v1v2v3]T,v1,v2,v3是线性化后系统的输入;
(9)
经反馈线性化, 方程组(4)变为
(10)
2.2 制导参数分析
在目标机动情况下, 设计末制导律时, 需要将拦截弹与目标之间的视线角速度趋近于x3=aTZ1/2x2b,x4=aTY1/2x2b。 令x3=p1+aTZ1/2x2b,x4=
当x3→aTZ1/2x2b,x4→aTY1/2x2b时,p1→0,p2→0。 假设拦截弹与目标相对速度近似不变, 因此选择v1=0,v2=λ1p1,v3=λ2p2, 则
(11)
(12)
考虑初始条件t=0时,x3=x3(0),x4=x4(0)得
(13)
则有
(14)
(15)
(16)
将上述参数代入式(8)得拦截弹加速度指令:
(17)
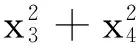
另外,λ取值越大, 指令过载在末制导初期也越大, 但末制导末端指令过载越小; 反之, 指令过载在末制导初期越小, 但末制导末端指令过载较大, 因此, 应合理选择λ。
3 直接力装置控制阀开启时间计算
本文用下式求解常推力作用时间:
(18)
式中:t1是控制信号更新周期;a11,a12是轨控装置提供的常值加速度;t21,t22是轨控装置提供的常值加速度作用时间。 这种方法可以消除距离误差, 但会产生速度误差:
(19)

剩余时间近似为tgo=x1/|x2|, 根据前文的脱靶量分析和制导精度需求, 可得
(20)
(21)
式中:l为制导精度;x1b为导引头盲区;x2b可近似为常值, 可得ε。
4 ENDGAME阶段仿真
仿真的初始计算条件设置为: 拦截弹机动能力≤6g; 拦截弹速度马赫数3; 目标速度马赫数5; 目标机动加速度1g; ENDGAME阶段距离15 km; 轨控装置延迟时间ms级。
迎头拦截条件下, 拦截器与目标的相对距离R(0), 视线方位角η(0)和视线高低角ζ(0)共5组如表1, 仿真结果见表2。
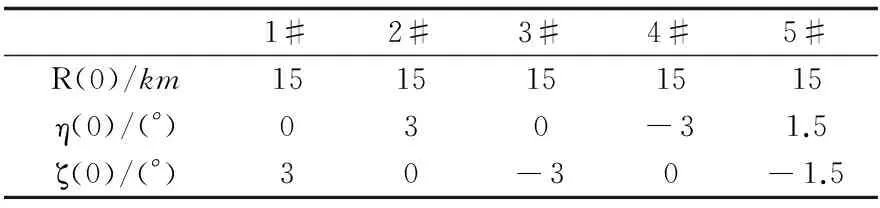
表1 仿真初始条件
仿真结果如图1~6所示。 所设计的制导律充分考虑了目标机动的情况, 视线角速度在进入制导盲区前保持小值; 导弹俯仰角和偏航角与视线角的偏差值保持小值且趋于稳定, 导引头正常跟踪目标; 导弹横滚角小于1°, 横滚角角速度趋于0; 导弹攻角和侧滑角能够稳定到小值, 避免导弹速度损失过快, 仿真中设定导弹纵向速度恒定; 直接力装置过载不可调, 根据喷管开启组合, 只能提供有限个点的过载值, 但满足过载小于6g的技术要求; 制导精度满足动能拦截的指标需求(拦截X-51目标, 要求脱靶量小于0.3 m)。

表2 仿真结果

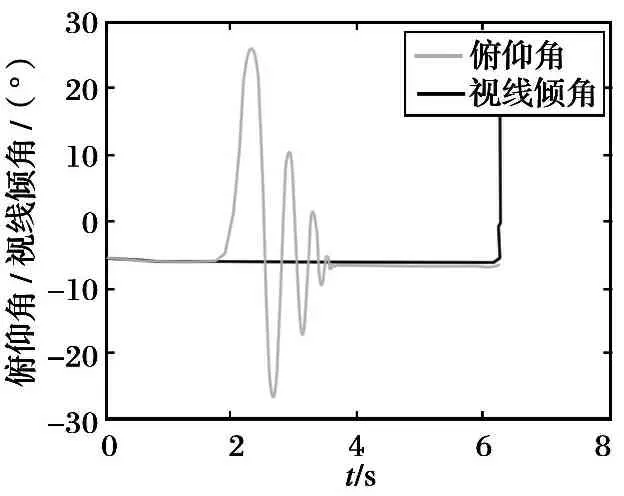
图1 弹目相对运动曲线
图2 导弹俯仰角和视线倾角变化图
Fig.2 Changing curve of the pitch attitude angle and the impact line-of-sight angle of missile
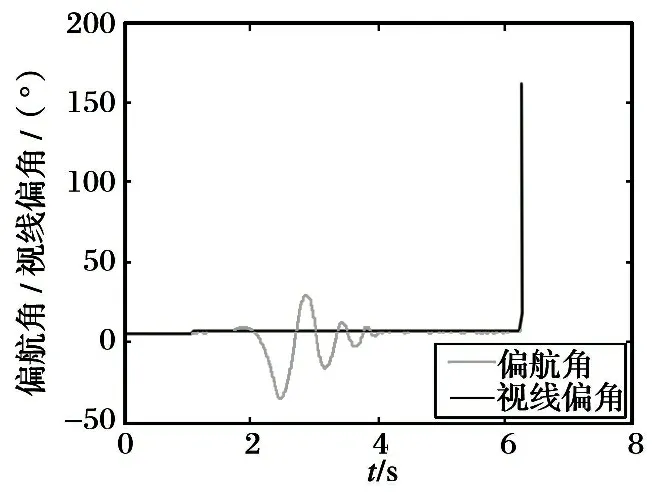
图3 导弹偏航角和视线偏角变化图
Fig.3 Changing curve of the yawing attitude angle and the deflection line-of-sight angle of missile

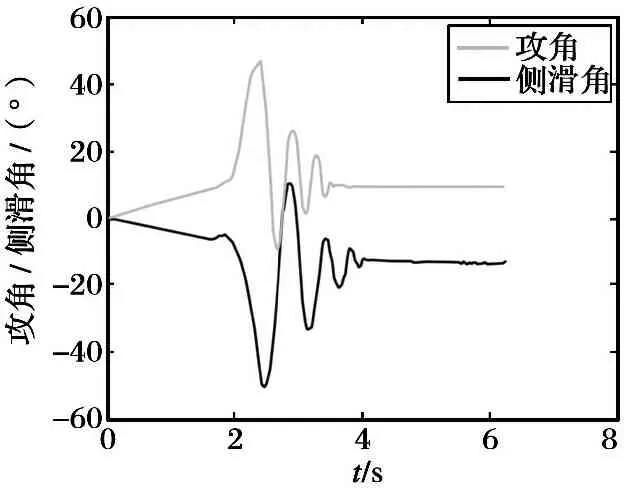
图4 导弹横滚角变化图
图5 导弹攻角和侧滑角变化图
Fig.5 Changing curve of the attack angle and the sideslip angle of missile

图6 导弹y向和z向过载变化图
Fig.6 Changing curve ofy-directional andz-directional overload of missile
5 结 论
综上可知, 本文所设计制导律避免了线性化带来的误差, 针对目标加速度特性推导出了视线角速度理想变化规律, 满足脱靶量有限时间趋于0的动能杀伤技术需求。 在后续工作中, 可以考虑将该方法推广到导弹制导与控制一体化设计中。
[1] 单晓林, 雷虎民, 肖增博, 等. 空基动能拦截弹寻的制导系统性能分析[J].航空兵器, 2014(4): 12-17. Shan Xiaolin, Lei Humin, Xiao Zengbo, et al. Performance Analysis of Homing Guidance System for Airborne Kinetic Energy Interceptor [J].Aero Weaponry, 2014(4): 12-17.(in Chinese)
[2] 凡国龙, 梁晓庚.临近空间拦截弹H∞末制导律设计研究[J].航空兵器, 2014(4): 8-11. Fan Guolong, Liang Xiaogeng.Design of H∞Terminal Guidance Law for Near Space Interceptor[J]. Aero Weaponry, 2014(4): 8-11.(in Chinese)
[3] 刘浩敏.一种新的最优空基反弹道导弹中制导方法研究[J].航空兵器, 2015(4): 12-15. Liu Haomin. Study on a New Air-Based Intercepting Ballistic Missile Midcourse Guidance Method[J]. Aero Weaponry, 2015(4): 12-15.(in Chinese)
[4] Bezick S, Rusnak I, Gray W S. Guidance of a Homing Missile via Nonlinear Geometric Control Methods[J]. Journal of Guidance, Control and Dynamics, 1995, 18(3): 441-448.
[5] Singh S N, Wang L. Output Feedback Form and Adaptive Control of a Nonlinear Aerolastic System[C]∥AIAA Guidance, Navigation, and Control Conference and Exhibit, Monterey California, 2002.
[6] Takehira T. Analytical Solution of Missile Terminal Guidance[J]. Journal of Guicance, Control and Dynamics, 1998, 21(2): 342-348.
[7] Huang J, Lin C F.A Modified CLOS Guidance Law via Right Inversion[J].IEEE Transactions on Aerospace and Electronic Systems, 1995, 31(1): 491-495.
[8] Leng G.Guidance Algorithm Design:A Nonlinear Inverse Approach[J].Journal of Guidance, Control and Dynamics, 1998, 21(5): 742-746.
[9] 胡恒章, 李君龙, 李风林.空间拦截系统的末制导律[J].哈尔滨工业大学学报, 1996, 28(6): 19-22. Hu Hengzhang, Li Junlong, Li Fenglin.A Terminal Guidance Law in Space Interception System[J].Journal of Harbin Institute of Technology, 1996, 28(6): 19-22.(in Chinese)
[10] 刘兴堂. 精确制导、 控制与仿真技术[M].北京: 国防工业出版社, 2006. Liu Xingtang.Precision Guide & Control and Simulation Technology[M].Beijing:National Defense Industry Press, 2006.(in Chinese)
[11] 钱杏芳, 林瑞雄, 赵亚男.导弹飞行力学[M].北京:北京理工大学出版社, 2003. Qian Xingfang, Lin Ruixiong, Zhao Yanan.Missile Flight Dynamics[M].Beijing:Beijing Institute of Technology Press, 2003.(in Chinese)
[12] 田宏亮, 梁晓庚, 贾晓洪, 等.只测视线角速度的目标可观性判据[J].北京航空航天大学学报, 2011, 37(5): 534-537. Tian Hongliang, Liang Xiaogeng, Jia Xiaohong, et al.Target Observability Criteria from Bearing-Rate-Only Measurments[J].Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(5): 534-537.(in Chinese)
[13] 田宏亮, 梁晓庚, 贾晓洪, 等. 视线角速度测量干扰对制导系统的影响[J]. 弹道学报, 2012, 24(3): 65-69. Tian Hongliang, Liang Xiaogeng, Jia Xiaohong, et al.Research of Line-of-Sight Rate Measurement Disturb on Navigation System[J].Journal of Ballistics, 2012, 24(3): 65-69.(in Chinese)
Designfor3DTerminalGuidanceLawofKineticEnergyInterceptor
TianHongliang,XuXiaoyan
(ChinaAirborneMissileAcademy,Luoyang471009,China)
Precise linear model of kinetic energy interceptor is extablished based on nonlinear feed back lineariztion theroy. According to the miss distance analysis result, guidance precision requirements and the characteristics of direct force control of kinetic energy interceptor, a3D terminal guidance law of kinetic energy interceptor is designed. The simulation result verifies the effectiveness of this terminal guidance law, which can meet the requirements of intercepting high-altitude and high-speed targets.
near space; hypersonic velocity; kinetic energy interceptor; guidance law; linearization
10.19297/j.cnki.41-1228/tj.2017.04.004
2016-11-02
航空科学基金项目(2016ZC12009)
田宏亮(1972-), 男, 河南鹤壁人, 博士, 高级工程师, 研究方向是飞行器设计。
田宏亮, 许晓艳 . 动能拦截弹三维末制导律设计[ J]. 航空兵器, 2017( 4): 21-25. Tian Hongliang, Xu Xiaoyan. Design for 3D Terminal Guidance Law of Kinetic Energy Interceptor[ J]. Aero Weaponry, 2017( 4): 21-25.( in Chinese)
TJ765; V448.133
: A
: 1673-5048(2017)04-0021-05
