基于能量平衡原理的水力劈裂能量耗散研究
2017-09-12张志敏高文华马向前
张志敏,高文华,马向前
(湖南科技大学 岩土工程稳定控制与健康监测省重点实验室,湖南 湘潭 411201)
基于能量平衡原理的水力劈裂能量耗散研究
张志敏,高文华,马向前
(湖南科技大学 岩土工程稳定控制与健康监测省重点实验室,湖南 湘潭 411201)
在页岩气开采中,水力劈裂总的能量耗散是评价页岩气是否具有可开采价值的一个重要指标。基于Griffith能量平衡原理,推导了平面应变问题水力劈裂过程中系统的总能耗的理论公式。分析了裂纹扩展速度、水的黏滞性和裂纹面的形态对系统总能耗的影响,得出了高脆性岩石材料在较低裂纹扩展速度下有利于节省水力劈裂的总能耗。同时推导了在等流量注水时单位时间的能量耗散表达式,随着裂纹的扩展,单位时间的能量耗散逐渐递减,因此,加压设备的功率主要取决于初始裂纹劈裂时的加载能力。该结论对于评估和改进水力劈裂开采页岩气有一定的借鉴意义。
页岩气;水力劈裂;能量耗散;裂纹
0 引 言
水力劈裂是一种利用高压水将地下岩石劈裂的施工技术,它主要应用于石油天然气、页岩气的开采,通过水力劈裂形成的裂纹,使储存在岩体节理孔隙中的原油和页岩气充分释放,并提高岩体的渗透性,到达提高开采产能的作用。同时水力劈裂还广泛应用于深部地应力的测量,地热开采等深部岩体地下工程等领域。在水力劈裂岩石的过程中,高压水流在裂纹表面施加了面力,改变了岩体内部原有的应力场,岩体应力场的变化又改变了裂纹的张开宽度,从而影响了裂纹内的水流特性。J.ADACHI等[1]指出岩石的水力劈裂过程是一个非常复杂的过程,它主要包括3个方面的耦合:作用在裂纹表面的高压水引起的应力应变场的改变,裂纹中水的渗流特性和尖端裂纹的扩展。这是一个非常复杂的数学问题,即使是平面问题的线弹性材料都非常复杂。许多学者[2-7]对水力耦合作用下的水力劈裂裂纹的萌生、扩展的力学机制进行了大量的研究,得出了许多有益的结论。这些结论对于指导我们改进和优化页岩气的开采工艺有着重要的指导意义。
在我国,可开采的页岩气的埋藏深度一般在地下1 500~3 000 m,远高于北美的开采深度800~1 500 m。由于埋藏深度的增加,我国页岩气的开采难度和成本远大于北美的页岩气开采。在2014年11月27日召开的中国页岩气发展大会上,中石化西南石油工程公司钻井研究院副院长罗朝东表示,在页岩气各个环节中,压裂占据60%成本,中国在降低压裂成本方面仍然有瓶颈。在页岩气开采过程中,水力劈裂总的能量耗散是压裂岩石成本构成的一个主要因素之一。如何节约压裂时总的能耗,是降低压裂成本的一个重要途径,关于这个方面的研究,可参考的文献很少。对于水力劈裂这样一个热力学系统,根据Griffith理论可知,这个系统的总能量消耗主要由储存在弹性介质中的应变能,总的水头损失和新裂纹表面形成消耗的表面自由能几个部分组成。系统的弹性应变能主要取决于岩石本身的力学参数、裂纹面的扩展长度、裂纹的张开量以及岩体所受的应力状态,根据相关学者通过理论和数值方法得到的研究成果[8-10]可以确定出这部分能量的大小。表面耗散能主要取决于裂纹的扩展路径和微裂纹的分布密度。周维恒[11]研究表明,在材料的断裂过程中,由于受细观结构不均性的影响,断裂过程区的微裂隙结构表现出一定的分形特性。谢和平等[12]对岩石材料的分形损伤、分形断裂、岩土介质的分形孔隙与分形节理等方面进行了详细研究。岩石断裂时的分形维数不仅影响了断裂过程的表面能,同时也影响了水在岩体中的渗透性能。微裂纹的发育以及宏观裂纹的形态,对于岩石的高压液体运输特性有着关键的影响。J.YANG等[13]采用PMMA材料制作了不同分形结构的单裂隙模型,通过高速摄像机测定水在裂纹中的渗流速度,研究了水在不同分形模型的渗透性,发现裂纹的分形维数对沿程水头损失较小,而对于局部水头影响非常显著。笔者基于Griffith能量平衡原理,推导了平面应变问题水力劈裂过程中系统总能耗的理论公式,分析上述因素对水压劈裂总能量耗散的影响,为改进水力劈裂施工技术提供了一定的参考依据。
1 Griffith能量平衡原理
笔者主要研究考虑渗流耦合的平面应变问题单裂纹的水力劈裂裂纹扩展。如图1,假定在岩体中存在一单裂纹,裂纹面平直光滑,初始裂纹的长度为l(0),初始裂纹宽度为0,流体为不可压缩的流体,且裂纹壁无水流交换,即流体在裂纹中渗流时不流失。当采用等流量注水时,裂纹在高压水作用下稳定扩展,根据Griffith能量平衡理论,这个系统的总能量消耗主要包括储存在弹性介质中总应变能UE,总水头损失UW和新裂纹表面形成消耗的表面自由能US这3个部分:
UA=UE+UW+US
(1)

图1 平面问题水力劈裂裂纹扩展简图Fig.1 Sketch of the crack development of hydraulic fracturing for the plane problem
2 水力劈裂下总能量耗散方程
2.1 弹性应变能
在水力劈裂过程中,裂纹的扩展速度取决于流体的注入量,同时流体的速度受制于裂纹的扩展速度,它们之间满足一个动态的平衡。材料的弹性能只取决于稳定状态的受力状态,而与加载路径无关。假定裂纹扩展中裂纹面上的压力函数与x的位置无关,在某一时刻t对应的裂纹长度上的压力函数为p(t)。I.N.SNEDDON等[14]基于弹性理论给出了裂纹表面压力p(t)和裂纹张开位移w的表达式:
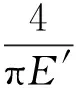
(2)
式中:E′为平面应变问题的弹性模量,E′=E/(1-υ2);υ为岩石材料的泊松比;l(t)在t时刻裂纹处于临界稳定状态下的半长,l(t)=l(0)+vt,v为裂纹尖端的扩展速度;G(s,x)为弹性内核积分函数:
(3)
根据线弹性断裂力学理论,可以得出在水压力p(t)作用下裂纹尖端的应力强度因子KI(t):

(4)
在等量注水条件下,随着注水量的增加,裂纹表面的水压力不断增大,根据式(4)可知,应力强度因子也逐渐增大。对于Ⅰ型裂纹的扩展,当应力强度因子等于材料的断裂韧度时,裂纹将沿着裂尖扩展。

(5)
式中:KIC为岩石材料的断裂韧度。
根据式(5)可得

(6)
根据弹性理论可知,弹性应变能与加载路径无关,因此储存在材料内部的弹性能只与稳定状态的应力应变有关:

(7)
2.2 裂纹面扩展的表面自由能
US为新形成裂纹表面所耗散的自由能,根据Griffith给出的裂纹前沿单位宽度上的裂纹系统表面能:
US=2γl
(8)
式中:γ为单位面积的自由表面能;l为水力劈裂过程中产生的新裂纹表面长度,l=l(t)-l(0)。
2.3 水在裂纹中渗流时的总水头损失
基于裂纹中水的渗流和裂纹变形满足体积守恒原理有,总的注入水量等于裂纹变形的体积改变量:

(9)
根据范宁公式[15-16],高压水在裂纹中渗流时的沿程水头损失Hf为

(10)


(11)
当裂纹面发生转向、形状发生急剧改变时,因漩涡区的存在、流动速度方向和大小的改变使该区域和附近区域受到集中阻力的作用,这种集中作用产生的流动阻力称为局部阻力,克服局部阻力引起的水头损失为局部水头损失Hl:

(12)
式中:ε为局部阻力系数。
由于假设裂纹面平直光滑,所以Hl=0,则
UW=Hf+Hl=Hf
(13)
3 模型分析
3.1 总能量损失表达式
裂纹在高压水的作用下扩展,将裂纹长度对时间t求导,可得裂纹的扩展速度:
(14)
裂纹中的水流速度取决于裂纹的扩展速度,当裂纹扩展到一定长度时,可知裂纹中水流的平均速度v1将远远小于裂纹的扩展速度。联立式(1)、式(7)、式(8)、式(9)、式(13)可得

(15)
从式(15)可得:① 在裂纹扩展速率较低时,由于水的动能损失的水头很小,总水头损失和裂纹的长度满足线性的关系。忽略岩石本身的渗流损失时,维持低的裂纹扩展速度有利于节省整个水力劈裂的能量耗散。② 当裂纹处于高速扩展时,水在裂纹中的沿程水头对系统的能量耗散则不能忽略,裂纹扩展速度的增大将增加水力劈裂的能量耗散。③ 随着劈裂液体的黏滞性的增加,液体的雷诺系数将减小,参数λ将显著增加,此时水在裂纹中消耗的能量也将显著增加。
3.2 单位时间的能量耗散率
在等流量注水时,单位时间的能量耗散决定了水力劈裂加压设备的功率,将式(15)对时间t求导可得
(16)
从式(16)可得,加压设备的功率主要取决于初始裂纹劈裂时的加载能力,随着裂纹的不断扩展,单位时间内的能量耗散率逐渐递减。
4 结 论
笔者通过能量守恒原理,得到水力劈裂过程中系统总能量耗散表达式,同过对该表达式进行分析,得到以下结论:
1) 根据水力劈裂过程总的流体体积平衡方程可知,采用小的注水速率可以得到低的裂纹扩展速度,在低速率的水力劈裂中,劈裂相同长度的裂纹可以节省水力劈裂的总能耗。
2) 液体黏滞性的增加,将提高液体在裂纹中渗流时的总能量耗散。
3) 在等流量注水时,单位时间的能量耗散随着裂纹的扩展逐渐递减,因此在选择加压设备时主要取决于初始开裂时所需要的最大功率。
4) 裂纹尖端的微裂隙网络,不仅增加了裂纹表面自由能的耗散,同时也增加了水在裂隙网络中渗流的总水头损失,因此,提高劈裂岩石的脆性指数将有利于减少微裂纹网络的产生,从而减少系统的总能耗。
[1] ADACHI J,SIEBRITS E,PEIRCE A,et al.Computer simulation of hydraulic fractures[J].InternationalJournalofRockMechanicsandMiningSciences,2007,44(5):739-757.
[2] SPENCE D A,SHARP P.Self-similar solution for elastohydrodynamic cavity flow[J].ProceedingsoftheRoyalSocietyofLondon, 1985,400(1819):289-313.
[3] LISTER J R.Buoyancy-driven fluid fracture:the effects of material toughness and of low-viscosity precursors[J].JournalofFluidMechanics, 1990,210:263-280.
[4] DESROCHES J.The crack tip region in hydraulic fracturing[J].ProceedingsoftheRoyalSocietyA,1994,447(1929):39-48.
[5] GARAGASH D,DETOURNAY E.The tip region of a fluid-driven fracture in an elastic medium[J].JournalofAppliedMechanics,2000,67(1):183-192.
[6] DETOURNAY E,GARAGASH D I.The near-tip region of a fluid-driven fracture propagating in a permeable elastic solid[J].JournalofFluidMechanics, 2003,494:1-32.
[7] GARAGASH D I,DETOURNAY E.Plane-strain propagation of a fluid-driven fracture:small toughness solution[J].JournalofAppliedMechanics, 2005,72(6):916-928.
[8] GARAGASH D I.Propagation of a plane-strain hydraulic fracture with a fluid lag:Early-time solution[J].InternationalJournalofSolidsandStructures, 2006,43(18/19):5811-5835.
[9] ADACHI J I,DETOURNAY E.Plane strain propagation of a hydraulic fracture in a permeable rock[J].EngineeringFractureMechanics,2008,75(16):4666-4694.
[10] MOKRYAKOV V.Analytical solution for propagation of hydraulic fracture with Barenblatt’s cohesive tip zone[J].InternationalJournalofFracture, 2011,169(2):159-168.
[11] 周维垣.高等岩石力学[M].北京:水利电力出版社,1990.
ZHOU Weiheng.AdvancedRockMechanics[M].Beijing:Water Resources and Electric Power Press,1990.
[12] 谢和平,于广明,杨伦,等.采动岩体分形裂隙网络研究[J].岩石力学与工程学报,1999,18(2):147-151.
XIE Heping,YU Guangming,YANG Lun,et al.Research on the fractal effects of crack network in overburden rock stratum[J].ChineseJournalofRockMechanicsandEngineering,1999,18(2):147-151.
[13] YANG J,ZHANG Q G,YANG Y M,et al.An experimental investigation on the mechanism of fluid flow through single rough fracture of rock[J].ScienceChinaTechnologicalSciences, 2013,56(8):2070-2080.
[14] SNEDDON I N,LOWENGRUB M.CrackProblemsintheClassicalTheoryofElasticity[M].New York:John Wiley & Sons,Inc.,1969.
[15] 刘鹤年.流体力学(第二版)[M].北京:中国建筑出版社,2004.
LIU Henian.FluidMechanics[M].2nd ed.Beijing:China Architect Building Press,2004.
[16] Roberson J A,Crowe C T.EngineeringFluidMechanics[M].3rd ed.Boston:Houghton Mifflin,1985.
(责任编辑:谭绪凯)
Energy Dissipation of Hydraulic Fracturing Based on Energy Balance
ZHANG Zhimin,GAO Wenhua,MA Xiangqian
(Hunan Provincial Key Laboratory of Geotechnical Engineering for Stability Control and Health Monitoring, Hunan University of Science and Technology,Xiangtan 411201,Hunan,P. R. China)
In the exploration process of shale gas,the total energy dissipation of hydraulic fracturing is one of the significant indicators to evaluate whether it is worthy to be explored.The theoretical formula of the total energy consumption in the process of the hydraulic fracturing for the plane strain problem was deduced based on the principle of energy balance of Griffith,and the impact of crack development speed,water viscosity and crack shape on the whole energy consumption was analyzed.It was concluded that the brittle rocks tended to be more beneficial to the conservation of energy dissipation of hydraulic fracturing with the lower crack speed.Furthermore,the formula of energy dissipation per unit time with the equal water injection was obtained.With the growth of crack,the energy dissipation per unit time decreased gradually;accordingly,the power of the pressurized equipment mainly depended on the loading potential of the initial crack fracturing.The conclusion can be used for reference to evaluate and improve the hydraulic fracturing exploration of shale gas.
shale gas;hydraulic fracturing;energy dissipation;crack
10.3969/j.issn.1674-0696.2017.08.10
2016-01-15;
2016-10-13
湖南省教育厅重点科研项目(16A073);湖南省研究生科研创新基金项目(CX2016B571;CX2016B561);湖南省岩土工程稳定控制与健康监测省重点实验室开放基金项目(E21622)
张志敏(1978—),男,湖南湘潭人,讲师,博士,主要从事岩土工程方面的研究。E-mail:hnustzhangzm@163.com。
TU41
A
1674-0696(2017)08-054-04
