行星齿轮典型断齿故障的动力学仿真*

杨文广,蒋东翔

(清华大学电力系统国家重点实验室 北京，100084)

行星齿轮典型断齿故障的动力学仿真*

杨文广,蒋东翔

(清华大学电力系统国家重点实验室 北京，100084)

基于一种改进的行星齿轮箱集总参数模型，将断齿故障等效到时变啮合刚度中，建立了直齿行星齿轮的太阳轮断齿故障、行星轮断齿故障和内齿圈断齿故障的动力学模型。以某单级行星齿轮为研究对象，考虑扭转方向外部激励，对其正常和各断齿故障状态下的动力学模型进行求解，对内齿圈垂直振动加速度信号进行分析。研究结果表明：只考虑扭转方向的外部激励时，正常状态下内齿圈最高点处的垂直振动加速度信号频谱中幅值最高的共振峰与模态能量分布相关；在各断齿故障状态下，内齿圈垂直振动加速度的有效值均大于正常值，时域波形中可看到不同形式的冲击，包络谱中可看到对应的故障特征频率及其倍频成分。

风力机；行星齿轮箱；断齿故障；动力学模型；故障机理

引 言

齿轮箱是双馈风力发电机组的关键部件之一。统计表明，风力机故障停机时间20%由齿轮箱故障引起，而且齿轮箱故障维修费用高，严重影响风力机的运行安全和经济效益[1]。由于行星齿轮箱结构复杂，同时承受时变风载和电气负载，其振动信号为非线性时变信号，因此研究齿轮箱在各种故障情况下的振动特性对于齿轮箱的振动故障诊断具有重要意义。

根据数据来源的不同，对齿轮箱振动故障特性的研究可大致分为动力学模型驱动和数据驱动。本研究内容属于前者。文献[2]将行星齿轮箱的动力学模型分为3类，即纯扭转模型、刚性多体动力学模型(也称集总参数模型)和柔性多体动力学模型。龙泉[3]建立了一个一级行星传动两级平行传动的齿轮箱的纯扭转模型，考虑刚度激励和误差激励，研究了齿根裂纹和齿面点蚀故障下的齿轮箱动态响应。Chaari等[4]建立了齿面点蚀和齿根裂纹故障状态下的行星齿轮集总参数模型，研究了齿轮在这两种故障激励下的振动响应。文献[5]建立了啮合刚度随齿根裂纹的裂纹深度变化模型，采用集总参数模型研究不同裂纹深度下平行齿轮副的振动响应。陈裴[6]利用ADAMS软件进行船用行星齿轮太阳轮断齿故障的仿真，指出太阳轮断齿故障时啮合频率周围出现调制现象，调制频率为其旋转频率乘以行星轮数。韩振南等[7]研究了平行传动齿轮系统中存在齿轮剥离故障时的动力学特性。文献[8]基于行星齿轮的振动响应特性和啮合冲击的传递路径，综合考虑各啮合成分之间的相位差，建立了行星齿轮箱的振动信号仿真模型。与纯扭转模型和柔性多体动力学模型相比较，集总参数模型可以以相对较小的计算复杂度、获得较准确的振动信号细节[9]，非常适合于齿轮箱故障机理研究。传统的集总参数模型建立在以行星架转速旋转的旋转坐标系中，存在壳体的旋转自由度难以约束等问题。

笔者提出了一种改进的刚性多体动力学模型[10]。在此基础上建立直齿行星齿轮的太阳轮断齿故障、行星轮断齿故障和内齿圈断齿故障的动力学模型，考虑扭转方向的外部激励和时变刚度等内部激励，采用隐式Newmark算法对模型求解。通过对仿真信号进行分析，从动力学角度揭示了行星齿轮箱在各种断齿故障状态下的动力学特性。

1 改进的行星齿轮箱集总参数模型

改进的集总参数模型直接选择惯性坐标系作为除行星轮外的其他部件的运动参考坐标系，避免了壳体旋转自由度难以约束的问题。对各行星轮，选择其运动参考坐标系作为绕太阳轮公转、同时以相同角速度自转的动坐标系。与传统模型相比，每个行星齿轮新增一个公转方向的角位移自由度。在该模型中，各行星轮的公转角位移与行星架的自转角位移相同。

笔者以直齿的行星轮和太阳轮啮合的啮合刚度矩阵为例，简单介绍该模型的推导过程，详细推导过程可参考文献[10]。记太阳轮为第1个齿轮，行星轮为第2个齿轮，则这两个齿轮间的啮合变形协调方程为

(1)

其中：θrevp为行星轮的公转角位移；φi为第i个齿轮对中心线到该齿轮运动参考坐标系x轴的夹角；xi,yi,θzi分别为第i个齿轮的水平振动、垂直振动和绕轴向(z轴)的扭转角位移；ri为第i个齿轮的节圆半径；rc为行星架的半径；广义自由度q=[x1,y1,θz1,x2,y2,θz2,θrevp]。

啮合力在第1个齿轮的各运动方向上的投影Fx1，Fy1，Tz1的计算公式为

(2)

啮合力在行星轮的各运动方向上的投影Fx1，Fy1，Tz1，Trevp的计算公式为

(3)

其中：Trevp为行星轮受到的啮合力在其公转自由度方向上的投影。

定义广义载荷为

F=[Fx1，Fy1，Tz1，Fx2，Fy2，Tz2，Trevp]

(4)

利用式(5)，得到行星轮与太阳轮啮合的啮合刚度矩阵Ke，该矩阵的大小为7×7

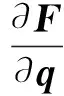
(5)

其他的刚度矩阵和阻尼矩阵可采用类似方法推导得到。根据各个齿轮间的相互作用关系，进行单元装配和约束处理，得到行星齿轮级动力学数学模型为

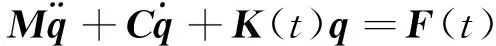
(6)

其中：M，C，K分别为总体质量、总体阻尼和总体刚度矩阵；F(t)为外部激励。

当阻尼项C中各个阻尼取值比较困难时，采用瑞利阻尼近似

C=αM+βK

(7)

其中：α，β为瑞利阻尼系数，根据具体情况选择。

为提高数值求解的稳定性，将式(6)进行变换

(8)

其中：Feq(t)为等效激励；F(t)为外部激励；K(t)q为内部激励；Kman为时不变的综合刚度矩阵。

2 断齿故障时变啮合刚度模型

齿轮副在一个时刻可能有多对齿参与啮合，一对啮合的直齿的啮合刚度随啮合位置在不断变化。对于行星齿轮系统，还需要考虑各对啮合齿轮之间的相对相位关系。因此，采用一个简化的行星齿轮时变啮合刚度模型[10]。对于断齿故障，当断齿参与啮合时，其提供的啮合力为0，可通过在时变啮合刚度模型中加入这一过程来模拟断齿故障。

以使用的行星齿轮为仿真对象，假设行星架转速恒为120 r/min，基于上述时变刚度模型仿真得到正常状态、太阳轮单齿断全齿故障、内齿圈单齿断全齿故障以及1号行星轮单齿断全齿故障的部分齿轮副的时变啮合刚度，如图1～4所示。将故障状态下的时变啮合刚度与正常状态下的相比，可以看到断齿会导致时变刚度中出现周期性的负冲击。从图2看到，当太阳轮发生断齿故障时，太阳轮与不同行星轮的时变啮合刚度中由于断齿导致的时变刚度负冲击之间存在120°相位差。从图4发现，断齿行星轮分别与太阳轮和行星轮啮合时的时变啮合刚度的负冲击之间存在180°相位差。

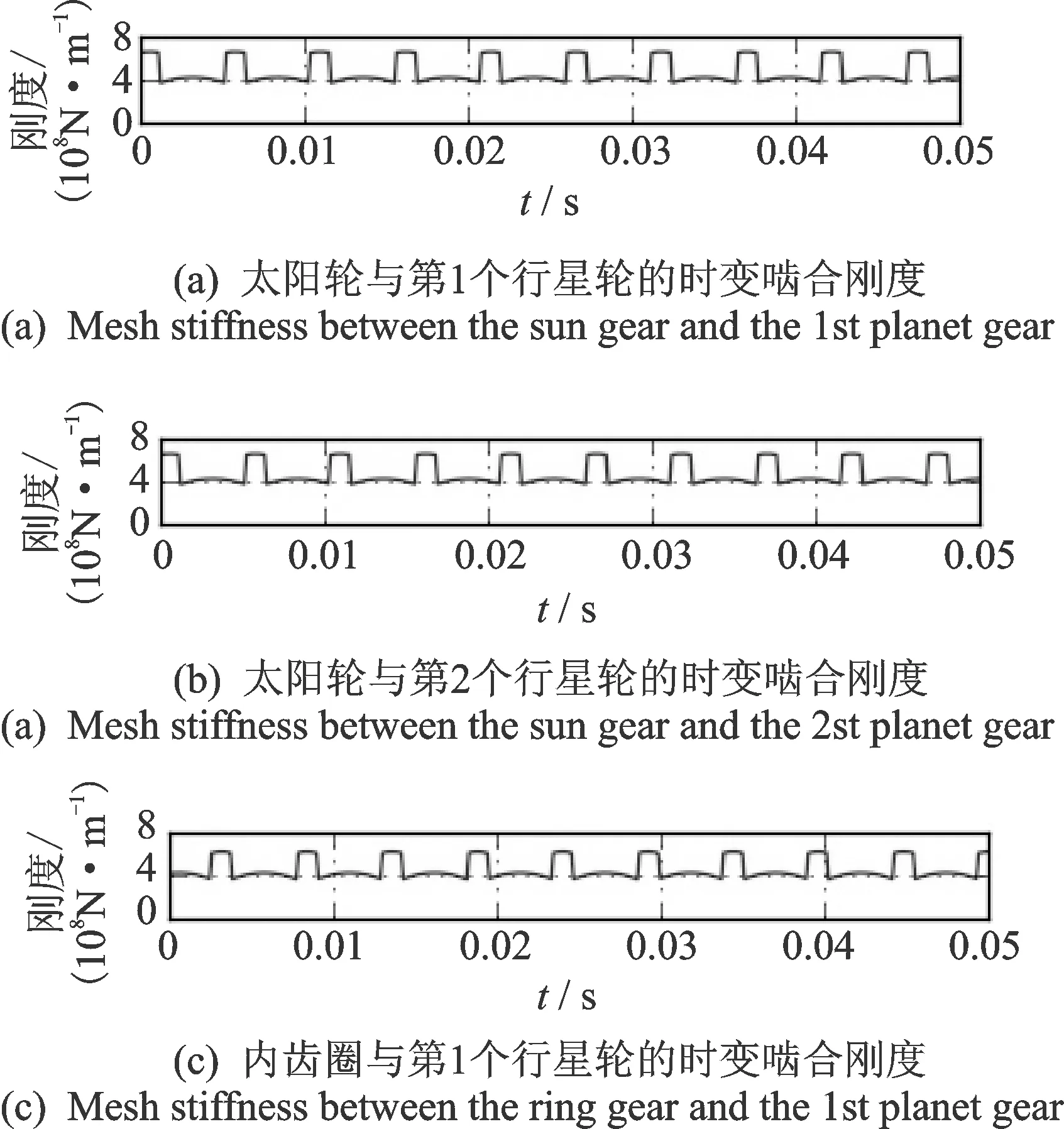
图1 正常行星齿轮中部分齿轮对的时变啮合刚度Fig.1 Mesh stiffness of some gear pairs in the healthy planetary gear

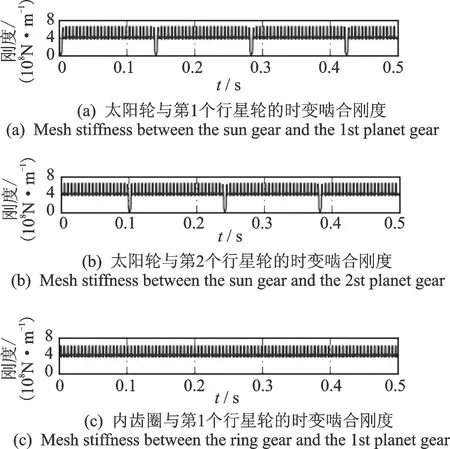
图2 太阳轮断齿故障时部分齿轮对的时变啮合刚度Fig.2 Mesh stiffness of some gear pairs in the planetary gear with sun tooth breakage fault

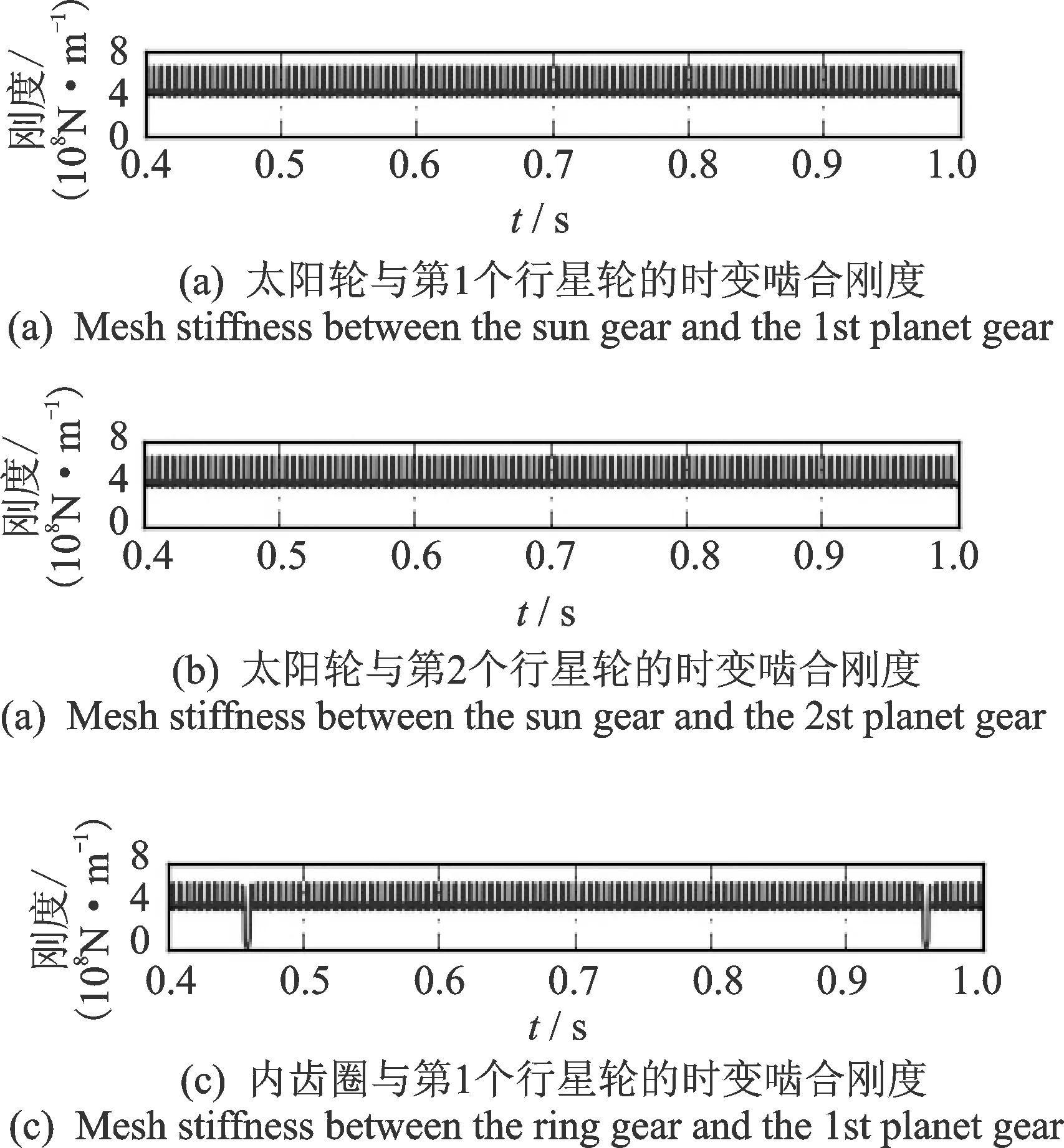
图3 内齿圈断齿故障时部分齿轮对的时变啮合刚度Fig.3 Mesh stiffness of some gear pairs in the planetary gear with ring tooth breakage fault

图4 行星轮断齿故障时部分齿轮对的时变啮合刚度Fig.4 Mesh stiffness of some gear pairs in the planetary gear with planet tooth breakage fault

3 行星齿轮参数及固有频率分析

选择某单级行星齿轮进行研究[11]，该行星齿轮系统有3个行星轮，等间隔布置，详细参数如表1所示。其中：下标s，p，c，r分别为太阳轮、行星轮、行星架和内齿圈；Ksn为太阳轮与行星轮的综合啮合刚度；Kpw为行星轮轴承的扭转刚度，忽略轴承的扭转刚度。通过计算可知，该级行星轮的传动比约为4.56，输入侧等效转动惯量。根据经验选择瑞利阻尼系数α=0．012 56，β=2．12×10-7。

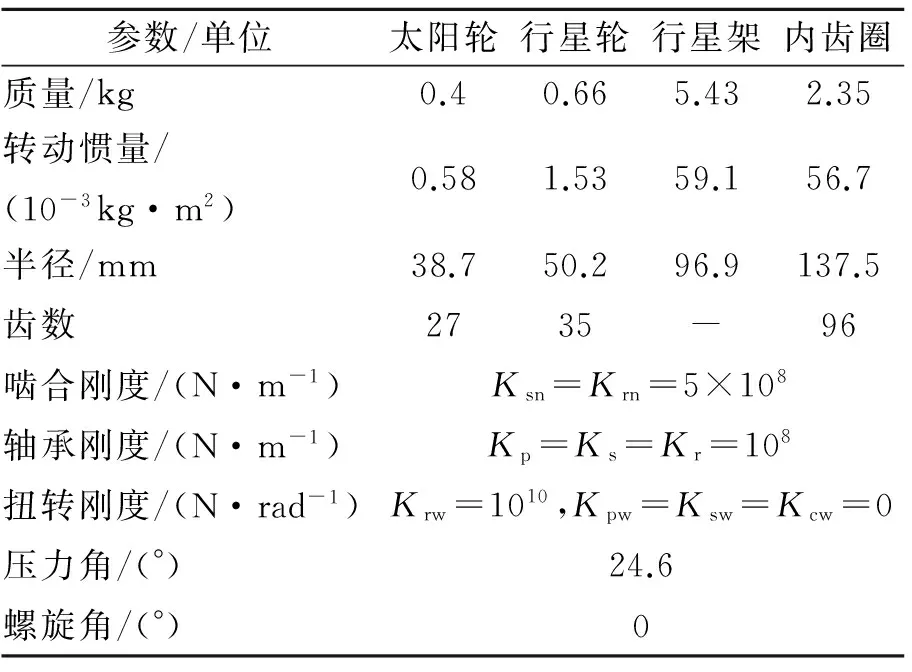
表1 行星齿轮的参数Tab.1 Parameters of the planetary gear

将正常及断齿故障状态下的时变刚度模型分别带入到改进的行星齿轮集总参数模型中，得到该行星齿轮在正常和各断齿故障状态下的动力学模型。

对该行星齿轮进行模态分析，得到的固有频率如表2所示。该行星齿轮系统共6个旋转固有频率和6个平动固有频率。由于模型中各轴承的水平和垂直方向的刚度相同，因此12个平动固有频率两两相同。

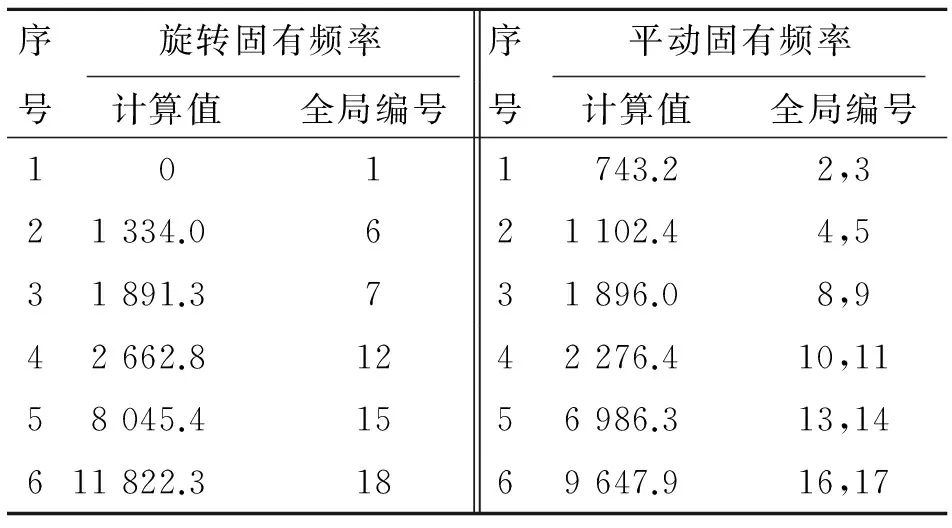
表2 固有频率计算结果Tab.2 Results of the modal frequency analysis

4 正常状态仿真与信号分析

只考虑扭转方向上的外部激励，取行星架上驱动扭矩F1(t)=10 Nm,太阳轮上负载扭矩F2为

(9)

其中：Tr为齿轮箱的传动比；v(t)为太阳轮的当前转速；C=120 r/min；t0为太阳轮转速首次达到转速C时的时间。

定性分析可知，t0时刻以前传动链空载运行，t0时刻负载接入，之后齿轮箱上的总扭矩达到动态平衡，转速将在转速C上下波动。可以估算t0≈CJ/F1=0．156s。选择定步长隐式Newmark算法[12]对模型进行求解，仿真步长取1×10-6s，时长为5 s，采样频率为25 kHz。

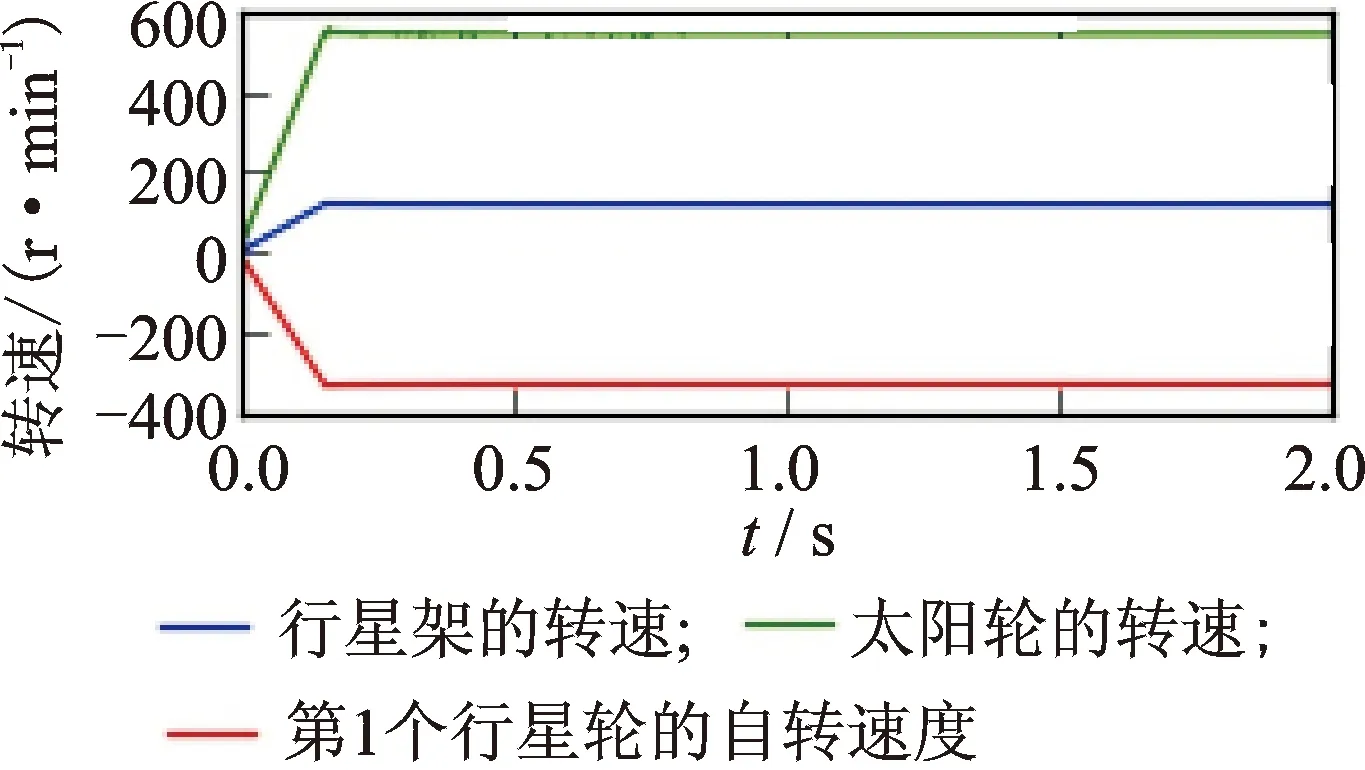
图5 正常状态下各部件转速Fig.5 The rotational speed of some components in the healthy planetary gear

进行正常状态下行星齿轮的瞬态动力学分析，得到部分组件转速的前2 s的时域波形如图5所示。仿真得到t0≈0．158 s，与理论估计值之间误差约为1.3%。取各转速最后1 s的数据进行平均，作为各部件的平衡转速，如表3所示。其中，各个理论值是以行星架转速120 r/min为基础，通过传动比关系计算得到。可以看到，各仿真值与理论值之间的误差在1%以内。

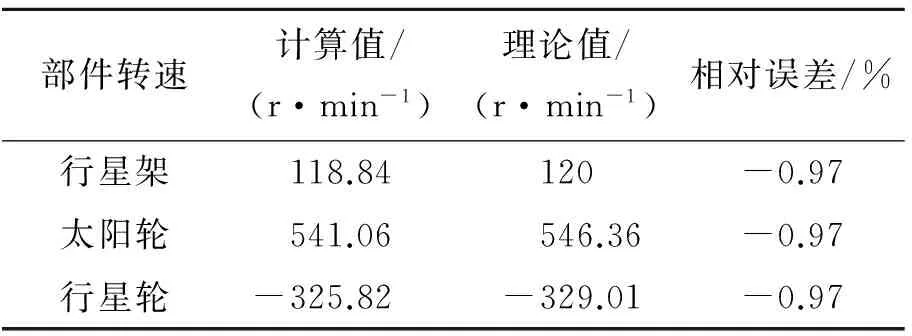
表3 转速的计算值与理论值对比Tab.3 Comparisons between the calculation rotational speeds and theoretical rotational speeds

实际振动传递器采集到的振动信号应对应仿真的垂直振动加速度和旋转振动加速度信号的合成，为简便起见，笔者取内齿圈最高点的垂直振动加速度1～5s的信号进行信号分析，该点处旋转运动在垂直方向上投影为0。其时域波形、频谱和包络谱分别如图6所示。由于仿真模型只考虑了扭转方向的外部激励以及内齿圈柔性等因素，因此仿真得到的垂直振动加速度很小。可以看到，最大的峰值在1103 Hz处，其次为743，1894和2277 Hz处，高频段也有两个共振区。与表2中的固有频率分析结果比较发现，这些频率值与横振固有频率相吻合。

图7为包络谱幅值的局部放大图,可以看到微弱的192 Hz啮合频率成分，低频区中的成分比较杂乱。这说明该频谱中的主要能量集中在固有频率附近，验证了行星齿轮振动信号中的共振调制现象。

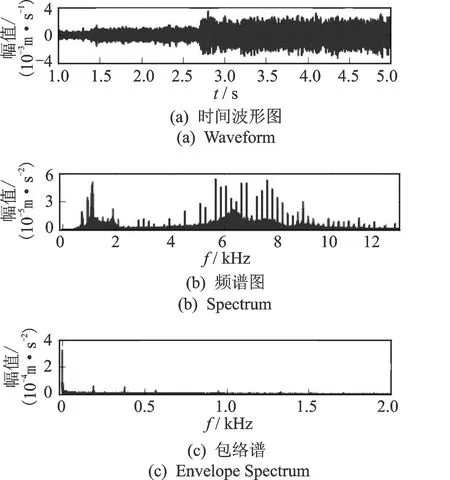
图6 正常状态下内齿圈垂直振动的仿真结果Fig.6 The simulated signal of the ring vertical vibration acceleration in normal state

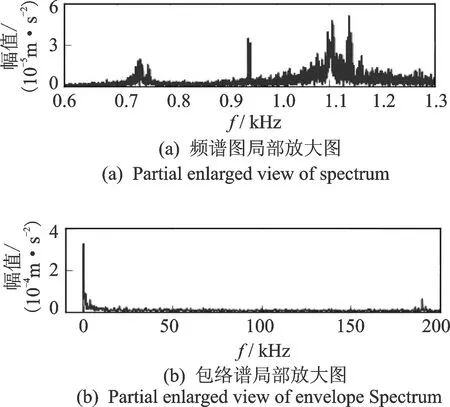
图7 正常状态下内齿圈垂直加速度频谱和包络谱局部放大图Fig.7 Partial enlarged view of spectrum and envelop amplitude spectrum of the ring vertical vibration acceleration in normal state

对频谱中的共振调制现象进行进一步分析。图8为系统各个平动模态的能量随组件的分布。模态能量的定义可参考文献[13]，图(a)～(f)分别对应第1个到最后一个平动固有频率。每一副子图均有4列，第1～4列分别对应该固有频率的模态能量在行星架、内齿圈、太阳轮和所有行星轮上的分布。可以发现，1103 Hz(对应着子图(b))的模态能量在内齿圈上分布的能量最大，其次为743 Hz。这说明内齿圈振动信号上的各固有频率附近的能量值与该固有频率对应的模态分布在该部件上的能量大小具有一定的关系。

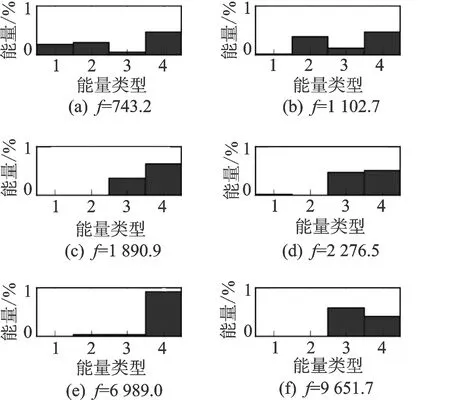
图8 各平动模态的能量随组件的分布Fig.8 Energy distribution over components of each modal

5 断齿故障仿真与信号分析

采用相同的外部激励，对各断齿状态下的行星齿轮进行仿真，仿真时长为5 s，得到的各个转速时域波形图与图5类似。行星架转速为120 r/min时，该行星齿轮太阳轮断齿故障特征频率fs约为7.11Hz，内齿圈断齿故障特征频率fr约为2 Hz，该频率同时也是行星架的旋转频率fc，行星轮断齿故障特征频率fp约为5.48 Hz。仍采用1～5 s的内齿圈垂直振动加速度信号进行信号分析，各状态下加速度信号的时域波形如图9所示。对比发现：各断齿故障产生的冲击导致该加速度的峰值明显增大；不同的齿轮断齿故障冲击造成的波形不同。

图9 各个状态下该加速度信号的时域波形Fig.9 Comparisons among the waveforms of in different states

以太阳轮断齿故障为例进行信号分析。该状态下内齿圈垂直振动加速度的时域波形、频谱和包络谱如图10所示。通过与正常状态下该信号的对比发现，频谱上1 103 Hz频率处的振动幅值增长最多，导致高频部分的成分被淹没。图11为故障状态下该信号的频谱和包络谱的局部放大图。与正常状态下的信号对比发现，故障状态下信号的频谱中存在明显的共振调制现象。从包络谱的局部放大图可以看到，除行星架的转频外，被调制的频率在低频段主要为7.11Hz以及其倍频，而且其3倍频较为突出，与行星轮的个数一致。

内齿圈断齿故障和行星轮断齿故障的内齿圈垂直振动加速度信号中也存在类似的共振调制现象。图12为不同状态下包络谱局部放大图的对比。可以发现，不同故障状态下被调制的频率成分不同，太阳轮和行星轮断齿故障状态下，被调制的主要频率是对应的故障特征频率，在其倍频成分中，3倍频成分较为突出，与行星轮的个数一致。行星轮断齿故障状态下，故障特征频率主要为其故障特征频率的偶数倍频，其中2倍频成分最突出，这是由于断齿的行星轮在一个旋转周期中先后与太阳轮和内齿圈啮合的原因。

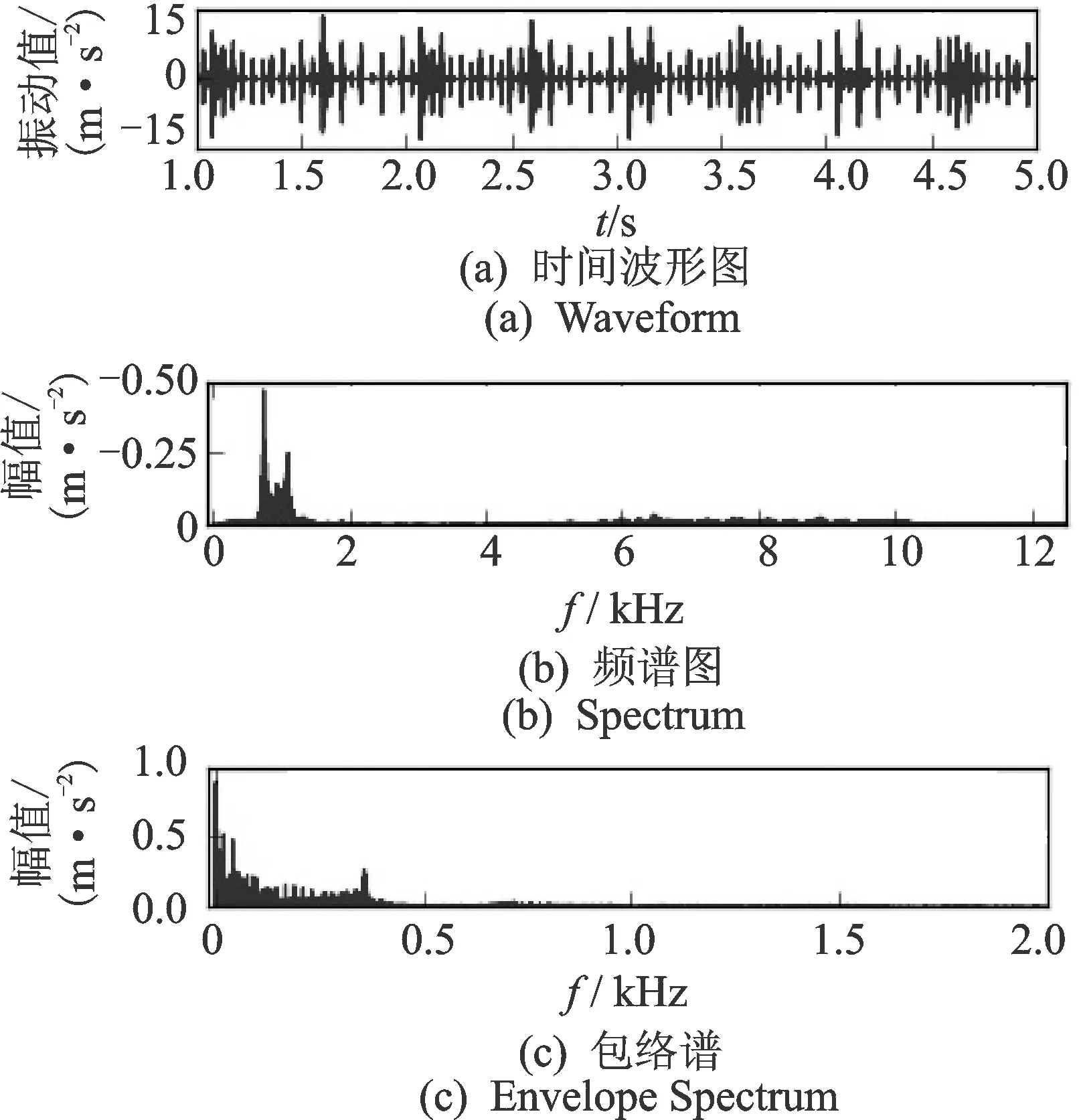
图10 太阳轮断齿故障状态下内齿圈垂直振动加速度仿真结果Fig.10 The simulated signal of ring vertical vibration acceleration in the sun tooth break fault state

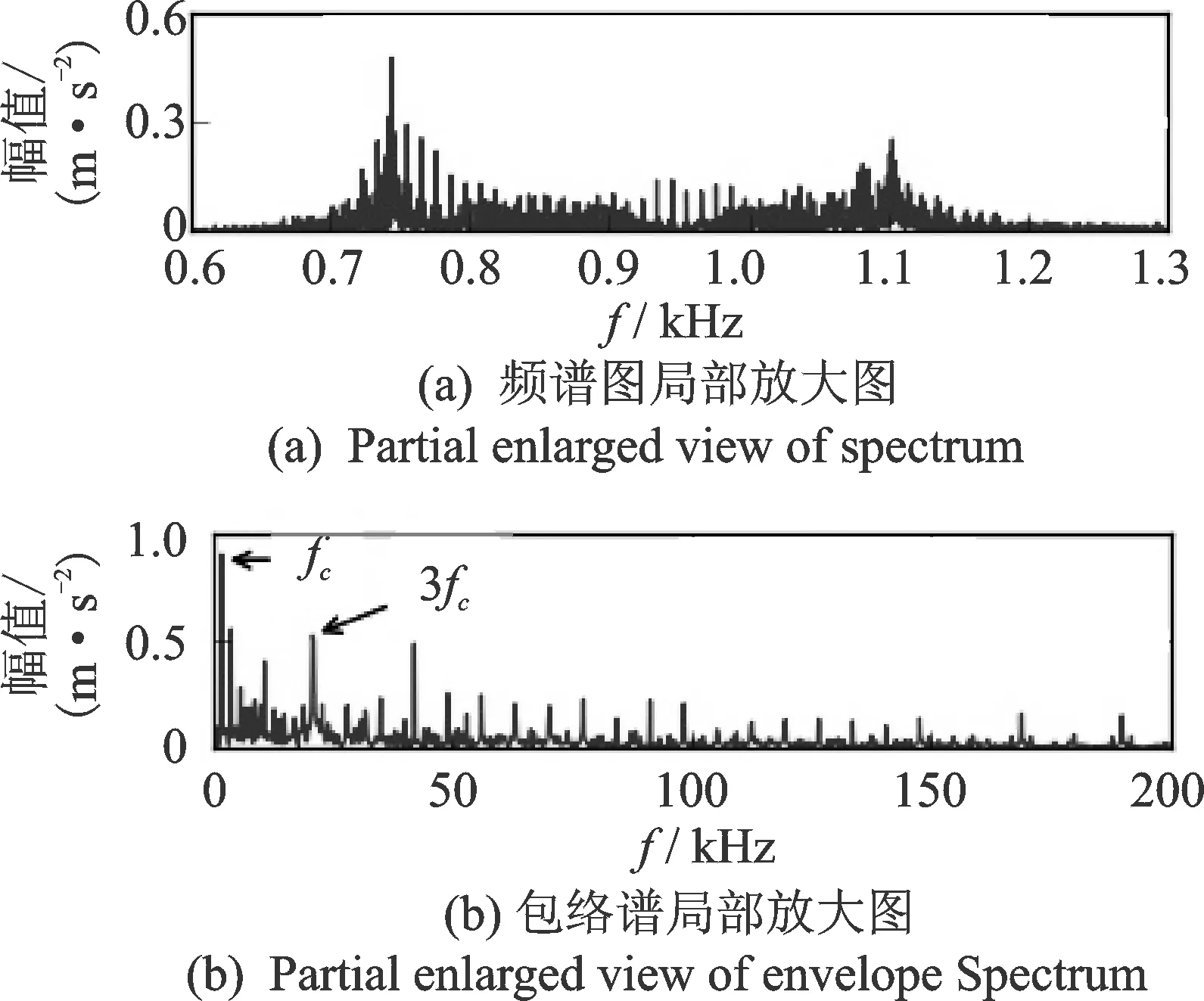
图11 太阳轮断齿故障状态下内齿圈垂直振动频谱和包络谱的局部放大图Fig.11 Partial enlarged view of spectrum and envelop spectrum of ring vertical vibration acceleration in the sun tooth break fault state

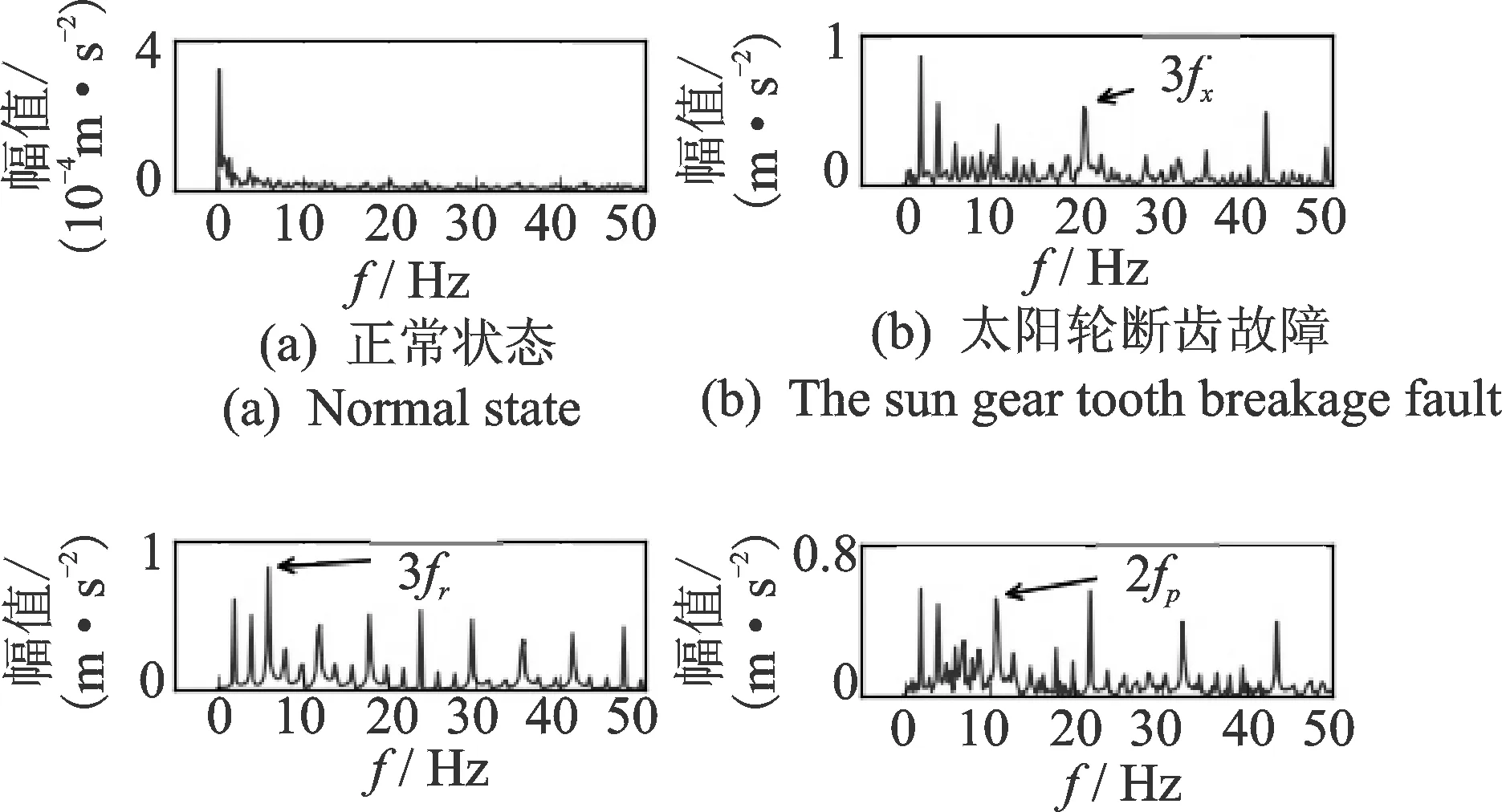
图12 内圈圈垂直振动加速度的包络谱局部放大图Fig.12 Partial enlarge view of the envelop spectra of the ring vertical vibration acceleration

共振解调分析(demodulated resonance analysis，简称DRA)是齿轮箱故障信号分析常用的方法，笔者选择高频区5 000～10 000 Hz的频带进行共振解调分析，得到各状态下包络谱信号的局部放大图如图13所示。与包络谱对比可以发现，共振解调得到的频谱更加干净，故障特征频率更加突出；对行星轮断齿故障，共振解调分析得到的故障特征频率的偶数倍频成分的幅值相对较大。这些现象与文献[14]的定性分析和实验结论一致。

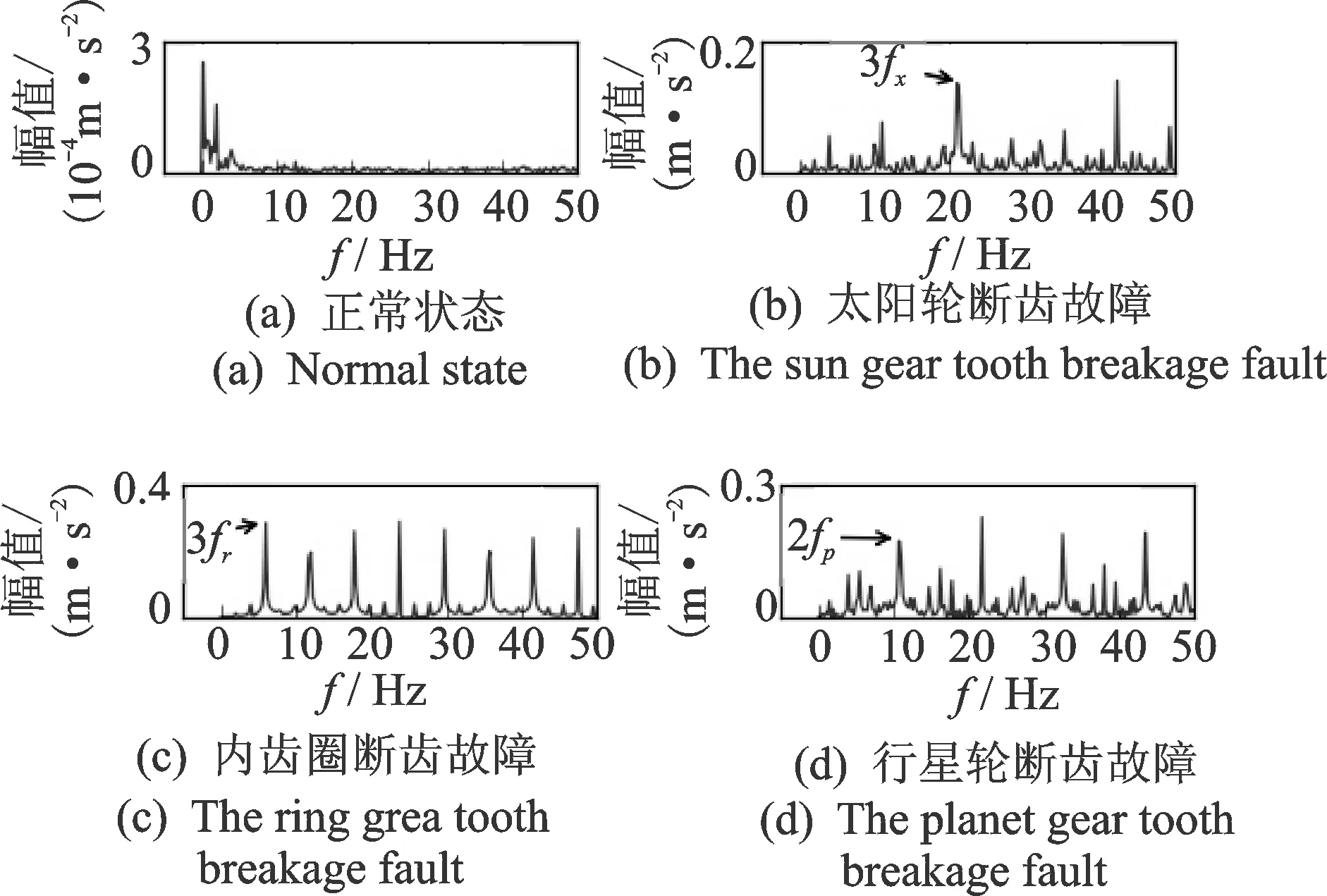
图13 内圈圈垂直振动加速度的共振解调分析局部放大图Fig.13 Partial enlarge view of the DRA of the ring vertical vibration acceleration

6 结 论

1) 只考虑扭转方向的外部激励时，齿轮箱最高点处垂直振动加速度信号中共振频率处的能量与其对应的固有频率的模态能量分布存在一定的关系。

2) 正常状态下，该振动加速度的调制频率中存在啮合频率，但较为微弱，低频区中的信号无明显规律。

3) 当出现断齿故障时，该振动加速度的有效值增大，频谱中出现了明显的共振调制现象。包络谱分析显示，被调制的频率成分为对应的故障特征频率及其倍频。

4) 对太阳轮和内齿圈断齿故障，除1倍频外，其3倍频成分也较为突出，与行星轮的个数一致；对行星轮断齿故障，故障特征频率的2倍频成分最为突出，这些结论与相关文献中的分析一致。

5) 建立的行星齿轮典型断齿故障的动力学模型可推广用于复杂外部激励作用下的故障机理研究以及多级行星齿轮箱和风力机传动链的故障机理研究。

[1] 陈雪峰，李继猛，程航，等.风力发电机状态监测和故障诊断技术的研究与进展[J].机械工程学报，2011,47(9):45-52.

Chen Xuefeng,Li Jimeng,Cheng Hang,et al.Research and application of condition monitoring and fault diagnosis technology in wind turbines[J].Journal of Mechanical Engineering,2011,47(9):45-52.(in Chinese)

[2] Peeters J.Simulation of dynamic drive train loads in a wind turbine[D].Belgium:Katholieke Universiteit Leuven,2006.

[3] 龙泉.风电机组齿轮传动系统动态特性及故障诊断方法研究[D].保定：华北电力大学,2012.

[4] Chaari F,Fakhfakh T,Haddar M.Dynamic analysis of a planetary gear failure caused by tooth pitting and cracking[J].Journal of Failure Analysis and Prevention，2006,6(2):73-78.

[5] Wu Siyan,Zuo Mingjian,Parey A.Simulation of spur gear dynamics and estimation of fault growth[J].Journal of Sound and Vibration,2008,317(3-5):608-624.

[6] 陈裴.船用行星齿轮断齿故障机理研究[D].上海：上海交通大学,2014.

[7] 韩振南，孙文婷，高建新.含轮齿剥落的齿轮系统动力学故障模拟[J].振动、测试与诊断，2012,32(1):101-104.

Han Zhennan,Sun Wenting,Gao Jianxin.Dynamics fault simulation of gear transmission system including spalling[J].Journal of Vibration,Measurement &Diagnosis,2012,32(1):101-104.(in Chinese)

[8] Lei Yaguo,Tang Wei,Kong Detong,et al.Vibration signal simulation and fault diagnosis of planetary gearboxes based on transmission mechanism analysis[J].Journal of Mechanical Engineering,2014,50(17):61-68.

[9] Ambarisha V K,Parker R G.Nonlinear dynamics of planetary gears using analytical and finite element models[J].Journal of Sound and Vibration,2007,302(3):577-595.

[10] Yang Wenguang,Jiang Dongxiang.An improved rigid multibody model for the dynamic analysis of the planetary gearbox in a wind turbine[J].Shock and Vibration,2016,2016(8):1-18.

[11] Lin Jian,Parker R G.Analytical characterization of the unique properties of planetary gear free vibration[J].Journal of Vibration &Acoustics，1999,121:316-321.

[12] Gasmi A,Sprague M A,Jonkman J M,et al.Numerical stability and accuracy of temporally coupled multi-physics modules in wind-turbine CAE tools[R].[S.l.]:Office of Scientific &Technical Information Technical Reports,2013.

[13] Lin Jian,Parker R G.Sensitivity of planetary gear natural frequencies and vibration modes to model parameters[J].Journal of Sound and Vibration,1999,228(1):109-128.

[14] 冯志鹏，赵镭镭，褚福磊.行星齿轮箱齿轮局部故障振动频谱特征[J].中国电机工程学报,2013,33(5):119-127.

Feng Zhipeng,Zhao Leilei,Chu Fulei.Vibration spectral characteristics of localized gear fault of planetary gearboxes [J].Proceedings of the CSEE,2013,33(5):119-127.(in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.04.019

* 国家自然科学基金资助项目(51174273)

2015-12-16；

2016-02-23

TK83;TH17

杨文广，男，1988年9月生，博士生。主要研究方向为风力机故障诊断。曾发表《An improved rigid multibody model for the dynamic analysis of the planetary gearbox in a wind turbine》(《Shock and Vibration》2016,No.8)等论文。 E-mail:ywg16@mail.tsinghua.edu.cn

蒋东翔，男，1963年2月生，教授、博士生导师。主要研究方向为动力系统设备故障诊断技术研究与应用。 E-mail:jiangdx@mail.tsinghua.edu.cn