多目标约束的电动汽车转向控制方法

田清华， 李巾帅， 邱永建

(1.石家庄职业技术学院 机电工程系，河北 石家庄 050081；2.吉利汽车研究院 设计部，浙江 杭州 311202)

多目标约束的电动汽车转向控制方法

田清华1， 李巾帅1， 邱永建2

(1.石家庄职业技术学院 机电工程系，河北 石家庄 050081；2.吉利汽车研究院 设计部，浙江 杭州 311202)

以八输入二自由度汽车模型为基础，根据并行优化算法理论和Pareto占优理论，采用多目标约束控制算法对车辆进行建模并建立目标函数.分两层设计汽车控制器，第一层获得目标空间的Pareto最优前沿,第二层把第一层中选择的区间目标作为约束优化的一个最重要指标.在Matlab环境下进行了仿真试验，以验证控制器的准确性.

多目标约束算法；电动汽车；控制器；转向控制

随着汽车保有量的增加，汽车的安全性越来越受到重视.为了保证汽车行驶时的稳定性，本文基于并行优化算法理论和Pareto占优理论[1-4]，采用多目标控制方法设计了控制器，以保证车辆在受到外界冲击时，仍能按照原轨迹行驶.

1 车辆动力学模型的建立

四轮独立转向电动汽车的模型如图1所示.

图1 八输入二自由度汽车模型

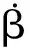
二自由度的车辆模型为：

(1)

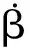
Fy=-Cαα

(2)

(2)式中，Cα为侧偏刚度.

4个车轮的侧偏角分别为：

(3)

综上可得，八输入二自由度的车辆模型为：

(4)

(4)式中，u=[δ1δ2δ3δ4Fx1Fx2Fx3Fx4],

l,a,b,c分别为轴距，质心距前轴、后轴、横轴的距离；Fxi为横向力.

使用sysd=c2d(sys,Ts)离散车辆系统模型后，车辆模型变为：

[β(k+1)γ(k+1)]T=G[β(k)γ(k)]T+Hu

(5)

(5)式中，k=1,2,3,4；G，H为A,B离散后的值.

2 控制器的设计

2.1 建立控制器的两层目标函数

式中，y∈Rq和μ(k)∈Rm分别是系统的控制输出和控制输入;控制约束为u(k)∈U;q为控制步长;p为输出维数;m为控制输入维数;k为迭代次数(参数).

本文控制对象模型为:

(6)

质心侧偏角β的取值为±0.1 rad;横摆角速度的取值为±0.15 rad/s；4个车轮转角的取值范围为|δi|≤0.15 rad，i=(1,2,3,4)；4个车轮纵向力的取值范围为0≤Fi≤100N，i=(1,2,3,4).由于4个转角δi和4个纵向力Fi范围相差较大，为了计算的准确性，对其进行归一化处理.用δi除以0.15，Fi除以100,得|δi|≤1,0≤Fi≤1，这样可减小计算误差.此时目标函数的最大范围为h1≤1.25，h2≤40，h1和h2分别是两个目标可以允许的最大值，表示两个目标函数最差可以允许的目标.

2.2 优化控制策略

两层结构的优化控制算法为：第一层获得Pareto的最优解集，第二层应用Matlab函数进行优化.

如图2所示，点A是理想点，将两个目标值都控制到A点很困难.为保证解存在，在目标空间选一个B点，将A点扩展为AB区域.

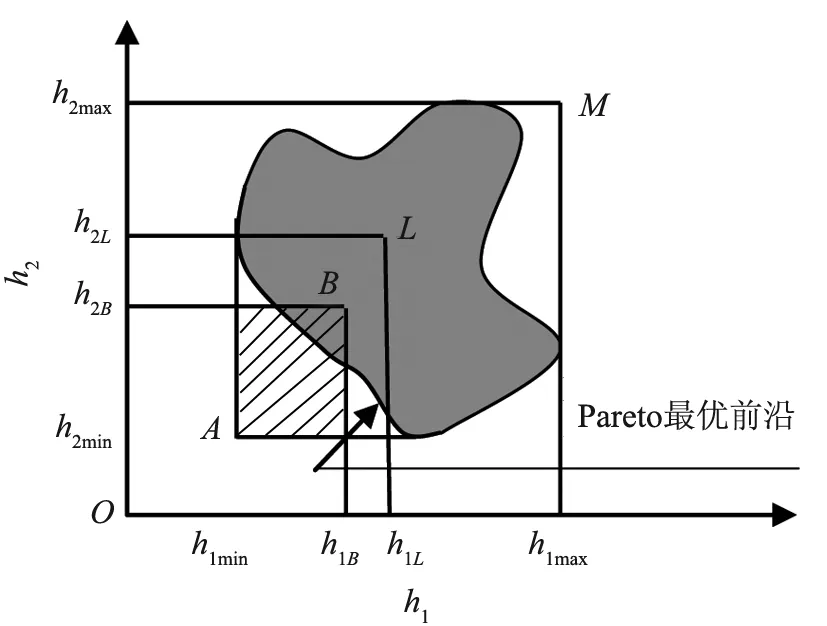
图2 Pareto最优前沿和区间目标的选择

第一层是找出合理的B点，分两步进行.

第二层是优化一个主要目标，将AB区域作为主要目标的约束进行优化.

2.3 I.C.-(X0)优化方法

横摆角速度和质心侧偏角均具有不确定性，故

(7)

其中，p=1，2，….

将建立的目标函数转换为u(k)和x(0)的函数，hi=hi(x(0);u(k),k=1,2,3,4,5),i=1,2

(8)

在I.C.-(X0)中，初始区域中每个点对应的Pareto最优解集叠加而成的区域称为I.C.-(X0)问题的带状Pareto最优前沿.

2.4 第一层控制器设计

实现Pareto最优解需要采用遗传算法，绘制Pareto分布图，多个解的阶和虚拟适应度如图3所示.

图3 两目标多个解的阶和虚拟适应度

图3中的8个解被分成3个阶，解1、解3、解5、解7的阶为1,解2、解6、解8的阶为2，解4的阶为3.一个解与同一阶所有解间的拥挤度称为虚拟适应度.

本文的两个初始状态均不确定，横摆角速度为±0.15 rad/s，质心侧偏角为±0.3 rad，根据(I.C.-(X0))问题的优化方法，在不同车速时对两变量进行正交试验，结果见图4.分别取间隔为±0.05 rad进行划分，种群个体数目取为50，变异概率取为0.9，遗传代数取为300，每种车速下均得出91个初始状态.本文仅列举出在3种不同车速下变量初值取为[±0.05，±0.05]的最优前沿.

图4(a)、图4(b)为低速、初始状态为[0.05,0.05]和[-0.05,-0.05]时的Pareto最优前沿.图4(c)、图4(d)为中速、初始状态为[0.05,0.05]和[-0.05,-0.05]时的Pareto最优前沿.图4(e)和图4(f)为高速、初始状态为[0.05,0.05]和[-0.05,-0.05]时的Pareto最优前沿.

图4 不同车速下的Pareto最优解分布图

依次计算出低、中、高3种车速下91个初值对应的Pareto最优前沿，并将91个最优前沿叠加，得出带状Pareto最优前沿，取出B点.不同车速下的Pareto最优前沿如图5所示，图5中L点[1.25，40]为目标函数可取的最大值.OL包围内的最优前沿上的点见表1.

图5 不同车速时的带状Pareto最优前沿

低速中速高速(0．30，37．46)(0．64，39．00)(0．80，39．20)(0．58，35．45)(0．86，37．48)(1．08，38．21)(0．32，36．59)(0．80，37．98)(0．90，38．20)(0．68，35．02)(0．94，37．46)(1．20，36．40)(0．56，36．01)(0．81，37．55)(1．00，37．86)(0．72，34．26)(1．31，37．46)(1．22，36．20)

B点通过多目标问题得到：

min maxhi(u;x(0))],i=1,2

(9)

在汽车低速行驶时，选取B点为(0.58，35.45)，h2的范围为[0，0.58]；在汽车中速行驶时，选取B点为(0.87，37.48)，h2范围为[0，0.87]；在汽车高速行驶时，选取B点为(1.08,38.21)，h2的范围为[0,1.08].将O点扩展为OB区域，在OB范围内两个目标都能实现.

2.5 第二层控制器设计

选目标函数h2作为进一步优化的指标，把第一层中得到的目标区域OB作为目标的约束.

应用Matlab中的fmincon函数优化，约束条件为|δi|≤0.15 rad，0≤Fi≤100 N，|δ1|>|δ3|，|δ1|>|δ4|，|δ2|>|δ3|，|δ2|>|δ4|及OB区域.

3 数学模型仿真试验

3.1 直线工况仿真试验

在Matlab软件中建立仿真模型，内外轮转角的关系为：

(10)

其中，β和α分别为内外轮转角；B为轮距；L为轴距.速度为15 m/s，侧偏角为0.02 rad时，质心侧偏角β和横摆角速度γ的响应曲线分别如图6(a)、图6(b)所示.图7、图8为4个车轮转角和纵向力的变化曲线.

图6 直线仿真试验曲线

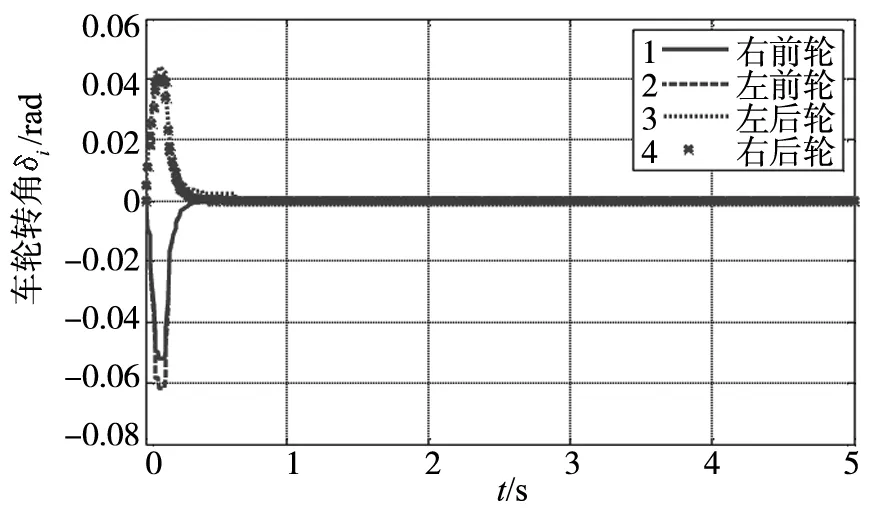
图7 4个车轮转角变化曲线

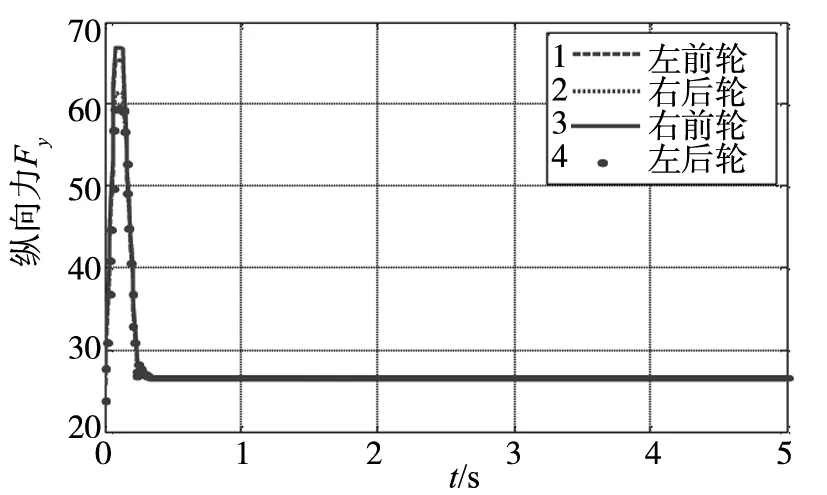
图8 4个车轮纵向力变化曲线

试验结果表明，直线行驶情况下，车辆受到外界干扰时，质心侧偏角和横摆角速度在较短时间内就能达到平衡，说明控制器起到了很好的调节作用.

3.2 道路试验仿真

笔者对此进一步进行了道路仿真试验，建立车辆、行人、道路的闭环仿真试验.道路模型选用单移线，满足(11)式.

(11)

仿真结果如图9-图11所示.图9为轨迹跟踪仿真图，可以看出，汽车在所设计控制器的作用下很好地跟踪了目标轨迹.图10(a)、图10(b)为横摆角速度及质心侧偏角的响应曲线.图11为车轮4个转角的角度变化曲线.可以看出，在车辆进行高速转弯时，前轮转角大于后轮转角，控制器较好地维持了车辆的稳定性.

图9 行驶轨迹仿真图

图10 道路仿真试验结果图

图11 四个车轮转角变化情况

[1] 刘战芳.4WS车辆的建模和控制方法研究[D].合肥：合肥工业大学，2008.

[2] MUSKE K,PEYTON J.Multi-objective Model-based Control for an Automotive Catalyst[J].Journal of Process Control,2006,16(3):15-18.

[3] DE RUITER A,LIU H.Control Design Decoupling for Two-way Coupled Systems[M].Taibei:International Conference on Control Applications,2004:776-781.

[4] 胡庆松.冲突多目标相容优化控制[D].上海:同济大学，2009.

责任编辑：金 欣

Special control method of electric vehicle with multi-objective constraints

TIAN Qing-hua1, LI Jin-shuai1, QIU Yong-jian2

(1.Department of Mechanics and Electrics, Shijiazhuang University of Applied Technology, Shijiazhuang, Hebei 050081, China;2.Department of Designing, Geely Automobile Research Institute, Hangzhou, Zhejiang 311202, China)

Based on the parallel optimization algorithm and Pareto dominance theories, a vehicle model is established and the objective function established by the eight input two degree of freedom vehicle model. The algorithm is divided into two layers, the first layer of which is to obtain the target space of the Pareto optimal front, and the second layer of which is, as the most important index of constrained optimization, to carry out the simulation test in Matiab environment to achieve the accuracy of controller.

multi-objective algorithm; electric vehicle; controller; steering control

2016-11-04

田清华(1977-)，女，河北栾城人，石家庄职业技术学院副教授.

1009-4873(2017)04-0012-05

U469.72

A