基于相关性判别分析的人脸图像分类算法
2017-09-11刘庆新陈支泽
尹 茜 刘庆新 陈支泽
(1.常州信息职业技术学院 江苏常州 213164; 2.上海诺基亚贝尔有限公司 上海 201600)
基于相关性判别分析的人脸图像分类算法
尹 茜1刘庆新1陈支泽2
(1.常州信息职业技术学院 江苏常州 213164; 2.上海诺基亚贝尔有限公司 上海 201600)
针对目前的判别分类方法不能有效分析数据之间相关性的问题,提出新的判别分类算法,并将其应用于人脸图像识别。首先,将传统的相关性分析模型拓展成有监督的形式,分别设计提取类内和类间相关性特征的目标函数,寻找投影变换以最大化类内相关性特征并且最小化类间相关性特征;进一步,对样本数据进行判别分析,使得投影之后同类样本之间散度最小化并且异类样本之间散度最大化;最后构建约束形式的相关性判别模型进行优化求解,并使用最近邻分类进行分类。实验结果表明,在AR人脸数据集上与对比算法相比能够将分类识别率提高1.01%~5.58%,在FERET人脸数据集上与对比算法相比能够将分类识别率提高1.87%~5.69%,实验结果与理论分析数据相符合,本算法能够有效地提高分类精度。
相关性分析; 判别学习; 人脸图像; 分类; 机器学习
人脸图像分类及识别是计算机视觉、机器学习和模式识别等领域活跃的话题之一,特别是近些年来,伴随现代通信及信息技术的蓬勃发展,人脸识别在很多领域都得到了广泛的应用。现代人脸图像具有形式多样化、图像维数高以及图像形态复杂等特点,如何有效地处理这些图像,不仅是图像处理领域的一大挑战,也成为很多相关领域的热点课题。最近20年,许多研究者围绕人脸图像分类展开了广泛而深入的研究,比如基于统计学的分类方法,如贝叶斯算法[1](Bayesian)、K近邻算法[2](K-Neighbor Nearest, KNN)、基于案例的推理和回归分析[3](Regression Analysis)等;基于机器学习的分类方法如决策树[4](Decision Tree, DT)、支持向量机[5](Support Vector Machine, SVM)等;神经网络方法如BP神经网络[6]、RBF神经网络[7]以及最近10年迅速发展的深度神经网络[8]等;基于局部图像描述的分类方法如Gabor小波变换方法[9]、局部二值模式[10](Local Binary Pattern, LBP)等;基于关联规则分类[11]以及其他的分类方法。
尽管目前出现了很多人脸图像分类方法和应用实例,但是这些方法依然存在其局限性。比如K近邻算法是一种“懒散”式的学习方法,并且随着样本类别及个数的增加计算量将大大增加;朴素贝叶斯算法要求的理论前提较为苛刻,这种前提条件在现实当中难以满足;SVM算法没有通用的方法去处理非线性数据,需要谨慎选择核函数;神经网络方法需要训练大量的参数,因此时间成本较大;决策树算法则容易出现过拟合的问题,并且忽略了图像数据之间的关联信息等。
人脸图像样本之间通常存在着一定的相关性(或判别)信息同时摒弃无用的相关(或判别)信息成为分类的关键所在,基于此动机,一些经典的特征提取方法被用于人脸图像分类,如主成分分析[12](PCA, Principal Component Analysis, PCA)、线性判别分析[13](Linear Discriminant Analysis, LDA)以及他们的扩展方法等,这些方法通常通过寻找一个投影变换矩阵,将原始样本投影至低维子空间,不仅可以达到降维的目的,而且使投影后子空间中的新样本具有特殊的性质。利用分析人脸样本之间的相关信息,典型相关性分析[14](Canonical Correlation Analysis, CCA)、半监督CCA(SCCA, Supervised Canonical Correlation Analysis)[15]以及双重相关分析(IISCA, Intra-View and Inter-View Supervised Correlation Analysis)[16]也被提出用于改善人脸的分类效果。
本文提出一种基于相关性判别分析的人脸图像分类方法(CDA, Correlation Discriminant Analysis),其创新工作如下:其一,能够同时进行判别分析和相关性分析,进行相关性分析的目的是最大化数据集中的类内相关信息,最小化类间相关信息,从而提取有利于分类的有效关联信息;其二,在相关性分析的基础上进行判别分析,进一步达到提高分类精度的目的。
1 典型相关分析
(1)
利用拉格朗日乘子法可以对式(1)中的模型进行求解。
2 本文算法
本文提出的CDA算法可以看成两个并行进行的部分:相关性分析部分和判别分析部分。对于相关性分析部分,寻求投影向量满足最大化类内相关特征,同时最小化类间相关特征的原则;对于判别分析部分,利用LDA算法,通过寻求最佳投影向量使模型满足Fisher判别准则,从而使投影变换之后的同类样本聚集异类样本分散。下面给出算法的数学模型描述以及相关推导过程。
2.1 CDA模型描述
考虑经过标准化之后的原始图像样本x,相应的样本集合为X,现在考虑求解投影变换v,使得投影之后的样本能够满足判别分析模型和相关性分析模型:
F(v)=D(v)+αC(v)
(2)
式(2)中F(v)表示CDA的目标函数,D(v)为判别分析项,C(v)为相关性分析项,α为平衡因子,用于平衡两项,从模型可以看出两项分析是同时进行约束的。下面分别对这两项进行设计。
2.2 相关性分析项
本文对典型相关分析进行改进,设计改进的相关性分析项的目的在于提取有利于分类的相关信息,同时去除不利于分类的相关信息,和典型相关性分析项不同,其分别包含类间、类内相关信息的分析,即通过该项保留图像之间的同类相关信息,并且去除图像之间异类的相关信息。因此C(w)项的设计应该包含有两部分:
C(v)=CW(v)-βCB(v)
(3)
式(3)中CW(v)为类内相关性分析项,CB(v)为类间相关性分析项,参数β为两者之间的平衡因子。
2.2.1 类内相关性分析项
对于式(3)中的CW(v)项,其定义了图像样本中的类内相关性特征,通过对典型相关分析中的相关系数进行拓展,考虑类别因素,得到的计算方式如下:

(4)
式(4)中xij表示第i类的第j个样本,c为样本类别个数。此外:
(5)
式(4)经过进一步化简可以表示为:
(6)
式(6)中D是一个对角矩阵,其矩阵的行和列均为nc,令A=XDXT,式(6)进一步变形为:
(7)
2.2.2 类间相关性分析项
类似的,对于CB(w),其定义了图像样本中的类间相关性特征,通过对典型相关分析中的相关系数进行拓展,考虑类别因素,得到的计算方式如下:
(8)
式(8)中的各项定义为:
(9)
式(8)经过进一步化简可以变形为:
(10)

(11)
2.3 判别项
设计判别项的目的在于寻求最佳投影向量,使得图像集中的类间散度矩阵的散度和类内散度矩阵的散度的比值最大化,此时可以利用LDA算法进行设计,判别性D(v)可以设计成:
(12)
其中SB和SW分别表示类间散度矩阵和类内散度矩阵,相应的计算方式分别如下:
(13)
(14)

2.4 CDA算法模型优化
综合2.2节中的相关性分析项和2.3节中的判别项,同时合并系数,式(2)可以变形为:
(15)
式(15)仅仅是一个目标方程,为了便于优化,给定约束条件vTSWv=1,并且缩放(15)中第二项分母中的因子[17],可以将其转化为以下形式的优化模型:
(16)
式(16)中的优化模型可以使用拉格朗日乘子法进行求解。定义带有惩罚项的拉格朗日函数
L(v)=vTSBv+λvTAv-γ(vTSWv-1)
(17)
在式(16)中,对v进行求导,并令其值为0可以得到
2SBv+2λAv-2γSWv=0
(18)
式(17)可以转化为一般性的特征方程问题:
(SB+λA)v=γSWv
(19)

2.5 分类过程
在上一节中给出了模型的求解过程,CDA算法的分类步骤如下:
1)原始图像样本预处理、标准化,并将数据集划分为训练集合本和测试集合;
2)计算特征方程(19)的前d个特征向量构成投影变换矩阵;
3)使用2)中的投影矩阵对样本进行投影变换;
4)对投影之后新的样本使用最近邻分类器分类并得到识别率。CDA算法分类过程见图1。

图1 CDA分类过程示意图
2.6 算法分析
从本文算法设计的模型来看,CDA具有其独特的优势:
1)CDA算法兼具相关性分析和判别分析,在判别分析的基础上保留有利于分类的相关信息,摒弃不必要的相关信息,因此相比较传统的LDA分类方法更加有利于分类效果的提升;
2)本文使用的相关性分析是一种有监督的分析方法,相比较于CCA算法,其重点在于分析图像样本中类内、类间的相关性特征,通过设计“最大化类内相关性并最小化类间相关性”的模型来改善分类效果;
3)从式(15)中的模型可以看出,经过化简的相关性分析项形式较为简洁,且与判别项类似,而同时优化这两项的优化过程也较为简单,最后可以归结为求解一般性的特征值与特征向量的问题,整个过程可以获得解析解,便于计算。
3 实验分析
本文选择AR和FERET人脸数据集作为实验数据进行实验,在实验过程中,选择PCA算法、LDA算法、CCA算法、SVM算法和IISCA作为对比算法。本文选择MATLAB R2012a作为实验工具,实验所用PC机配置为Intel 酷睿i7 6700 CPU,32 G内存。
3.1 数据集介绍
1)AR人脸数据集总共包含来自70位男性,56位女性的共3000多张图像,所有的图像分两个阶段采集得到,每个阶段采集了14张包含不同光照、表情或遮挡的768×576大小的图像。为了实验的准确性和效率,本文选择其中一个子集,该子集共有119个类,每类选取第一阶段的14张图像作为实验数据,并将原始图像预处理成60×60像素大小,图2为部分样本。


2)FERET人脸数据集总共包含来自200个人脸的2200张图像,所有的图像由不同的光照或者角度采集得到,原始图像像素大小384×256。由于原始图像像素较高,本文预先将图像处理成60×50像素大小,其中图3为部分样本。


3.2 实验设置
对于AR数据集,本文实验中共有119类,共进行20次分类识别率实验,每次实验随机选取每类中的7张作为训练样本,剩余的作为测试样本;类似地,对于FERET,同样也进行20次分类识别率实验,每次实验打乱样本标签随机选取其中的5张作为训练,其余的作为测试样本。
在实验过程中,为了避免算法出现奇异性问题同时缩短实验时间,除PCA算法本身以外,事先使用PCA算法对原始样本进行降维预处理,降维的具体维数可由循环挑选主元得到;在对比算法中,相关性算法使用监督的CCA方法,即式(15)中模型的第二项,对于SVM算法采用径向基核进行试验,本文算法中的参数λ在0.5和1.5之间能得到的分类效果较好,本文实验过程中通过循环获取最好的λ值。
3.3 实验结果及分析
最终得到两个数据集识别率波动图分别如图4、图5所示。
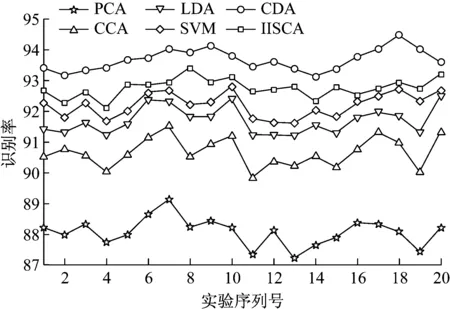
图4 AR人脸数据集识别率图
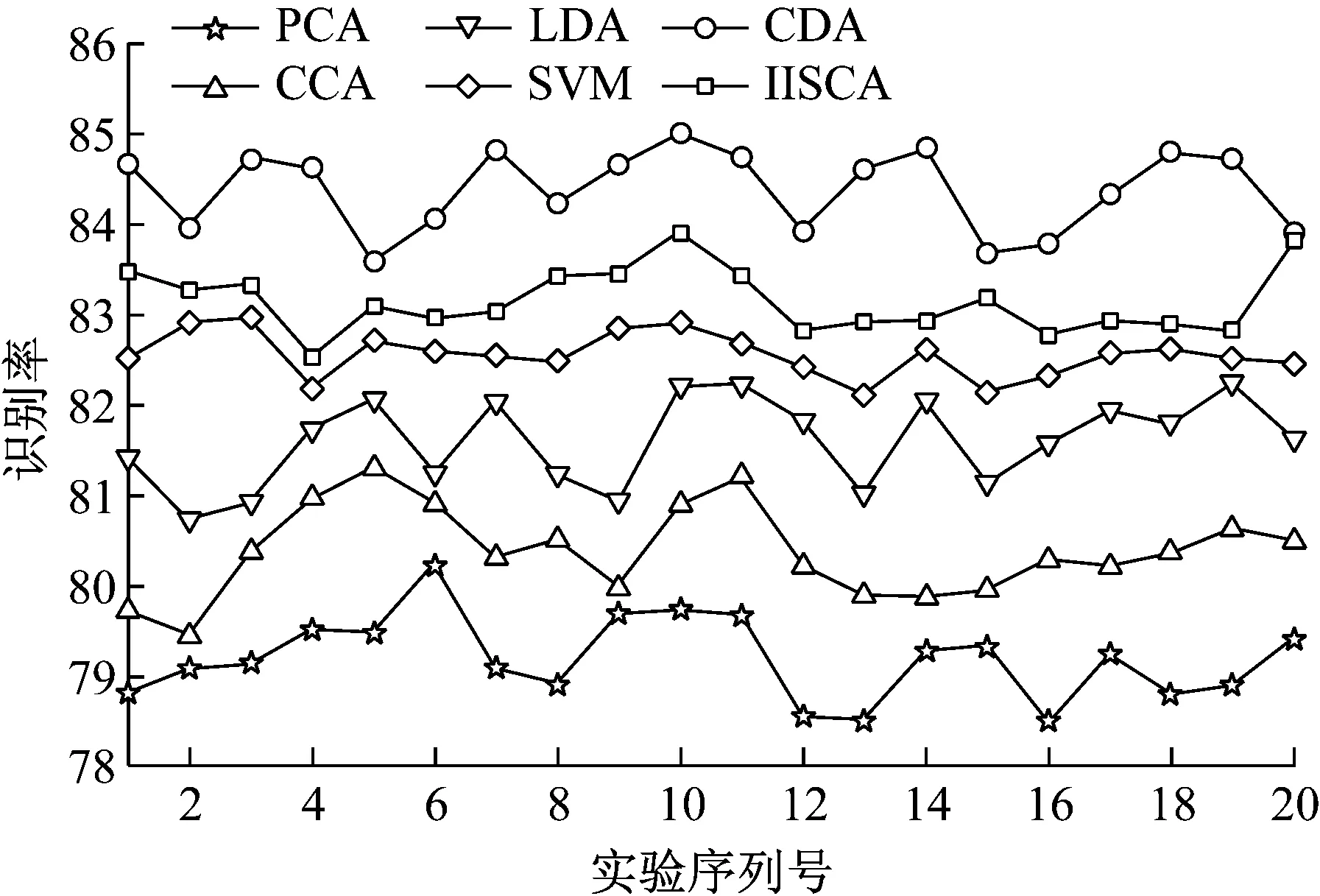
图5 FERET人脸数据集识别率图
从图4、图5可以看出,在AR人脸数据集上本文提出的CDA算法最终能够将识别率提高1.01~5.58%,在FERET人脸数据集上能够提高1.87~5.69%,分类识别率结果也反映了本文提出的CDA算法的有效性。究其主要原因,本文提出的分类模型不仅具有较强的判别能力,而且能够提取有效的相关信息,去除了不必要的关联信息,相比较而言,LDA是一种线性的有监督分类方法,并没有利用图像之间的关联信息;CCA本身如果单独使用进行分类,并没有合理地考虑潜藏在图像中的内部结构信息;对于SVM,虽然拥有较强的泛化能力,但是需要选择合适的核函数,而SVM本身也具有多种形式的模型,因此如何选择合适的参数也是一个问题,同时SVM也没有很强的判别分类能力。IISCA作为CCA的一种扩展方法,同时进行了视图内和外部的相关性分析,但是其并未考虑判别性。
4 结论
1)本文提出的CDA算法着重于提取图像中的判别相关特征,在改进相关性分析模型的同时提取判别特征,使得模型既能够提取有利于分类的相关信息,去除不利于分类的关联信息,又能增强模型的判别能力,因而能够从一定程度上改善分类效果。
2)需要指出的是,CDA算法具有一定的可扩展性,借助于核函数进行高维映射,能够使其更好地处理非线性问题,从而充分挖掘图像中的非线性信息。
另外,CDA算法可以作为一种特征融合的方法,使其适用于多特征融合或者多视图数据情况下的分类情形,今后工作将围绕以上两点展开。
[1] Williams C K I, Barber D. Bayesian classification with Gaussian processes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1998(12): 1342-1351.
[2] Weinberger K Q, Saul L K. Distance metric learning for large margin nearest neighbor classification[J]. Journal of Machine Learning Research, 2009(12): 207-244.
[3] Kurt I, Ture M, Kurum A T. Comparing performances of logistic regression, classification and regression tree, and neural networks for predicting coronary artery disease[J]. Expert Systems with Applications, 2008(1): 366-374.
[4] Friedl M A, Brodley C E. Decision tree classification of land cover from remotely sensed data[J]. Remote sensing of environment, 1997(3): 399-409.
[5] Pradhan B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS[J]. Computers & Geosciences, 2013,51: 350-365.
[6] Ren C, An N, Wang J, et al. Optimal parameters selection for BP neural network based on particle swarm optimization: A case study of wind speed forecasting[J]. Knowledge-Based Systems, 2014,56: 226-239.
[7] Tsekouras G E, Tsimikas J. On training RBF neural networks using input-output fuzzy clustering and particle swarm optimization[J]. Fuzzy Sets and Systems, 2013,221: 65-89.
[8] Hinton G, Deng L, Yu D, et al. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups[J]. IEEE Signal Processing Magazine, 2012(6): 82-97.
[9] Porter R, Canagarajah N. Robust rotation-invariant texture classification: wavelet, Gabor filter and GMRF based schemes[J]. IEE Proceedings-Vision, Image and Signal Processing, 1997(3): 180-188.
[10] Zhang B, Gao Y, Zhao S, et al. Local derivative pattern versus local binary pattern: face recognition with high-order local pattern descriptor[J]. IEEE transactions on image processing, 2010(2): 533-544.
[11] Karabatak M, Ince M C. An expert system for detection of breast cancer based on association rules and neural network[J]. Expert systems with Applications, 2009(2): 3465-3469.
[12] Candès E J, Li X, Ma Y, et al. Robust principal component analysis[J]. Journal of the ACM (JACM), 2011(3): 11.
[13] Bandos T V, Bruzzone L, Camps-Valls G. Classification of hyperspectral images with regularized linear discriminant analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009(3): 862-873.
[14] Kim T K, Cipolla R. Canonical correlation analysis of video volume tensors for action categorization and detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009(8): 1415-1428.
[15] Jing X Y, Hu R, Zhu Y P, et al. Intra-View and Inter-View Supervised Correlation Analysis for Multi-View Feature Learning[C]//AAAI. 2014: 1882-1889.
[16] Shen X B, Sun Q S. A novel semi-supervised canonical correlation analysis and extensions for multi-view dimensionality reduction[J]. Journal of Visual Communication and Image Representation, 2014(8): 1894-1904.
[17] Yang M, Sun S. Multi-view uncorrelated linear discriminant analysis with applications to handwritten digit recognition[C]//Neural Networks (IJCNN), 2014 International Joint Conference on. IEEE, 2014: 4175-4181.
[责任编辑:李娟]
Face Image Classification Algorithm Based on Correlation Discriminant Analysis
YIN Qian1LIU Qingxin1CHEN Zhize2
(1. Changzhou College of Information Technology, Changzhou 213164, China; 2. Shanghai Nokia Bell, Shanghai 201600, China)
Aiming at the problem that the existed discriminant classification method could not effectively utilize the correlative information on the data set, this paper proposes the discriminant algorithm in face image recognition. Firstly, it extends the correlation analysis to supervised model, designs the intra class and inter class correlation feature extraction function, and seeks the projection transformation which could maximize the intra class correlation feature and minimize the inter class correlation feature. Furthermore, discriminant analysis is performed, which makes the projected model maximize scatter value between different class samples and minimize scatter value between same class samples. Finally, it constructs constrained correlation discriminant model to solve the optimization and uses the nearest neighbor classifier to classify the samples. Experimental results show that, compared with other algorithm on AR face data set, the proposed algorithm can achieve recognition rate increase of 1.32%~5.58%; and compared with other algorithm on FERET face data set, the proposed algorithm can realize the recognition rate increase of 2.27%~5.69%. The experimental results are in agreement with the theoretical analysis data, and the proposed algorithm can effectively improve the classification accuracy.
correlation analysis; discriminant learning; face image; classification; machine learning
2017-04-30
常州市高技术研究重点实验室(CM20153001)
尹 茜(1980-),女,讲师,硕士,主要研究方向:机器视觉、智能控制
TP 391.41
A
1672-2434(2017)04-0018-06
