关于“高等材料力学”的一段史话

郭日修

(海军工程大学舰船工程系，武汉430033)

关于“高等材料力学”的一段史话

郭日修1)

(海军工程大学舰船工程系，武汉430033)

1947年秋开始，张维教授在清华大学招收固体力学研究生，并讲授“高等材料力学”，这是研究生的核心课程，内容以板壳理论为主.板壳理论是20世纪前三、四十年固体力学领域的重要研究成果，其处理问题的方法与材料力学一脉相承.张维教授开设的“高等材料力学”课，使研究生掌握近代应用力学的研究成果，更重要的是使研究生掌握近代应用力学处理问题的方法，具备研究解决工程中提出的新的固体力学问题的能力.

高等材料力学，力学史，方法论

1947年夏，张维教授应清华大学之聘在机械工程系任教，讲授工学院的应用力学(后称理论力学)和材料力学课程.1946年清华大学由昆明迁返北平，秋季开学后，这二门课由钱伟长教授讲授.抗战胜利后，清华大学工学院学生人数增加很多，工学院的力学课程须分开多班次开课，钱教授一人忙不过来，所以学校于1947年增聘张维教授与钱教授共同承担、分班讲授工学院的应用力学和材料力学课程.与此同时，张维教授还在清华大学土木工程系招收研究生，研究方向是固体力学.张教授给研究生讲授的“高等材料力学”课程是研究生的主课.当时清华大学还处于由内地返迁后的恢复、重建阶段，招收研究生的教授不多，张维教授在土木工程系招收研究生、开设“高等材料力学”课程，引起很多人关注.“高等材料力学”这门课此前在清华大学没有开设过，国内其他高校可能也没有开过这门课，因此来听课的人较多，除研究生外，还有不少工学院的助教和个别本科高年级学生.

在“高等材料力学”的第一课，张维教授介绍了课程内容.大体包括4部分:第 1部分，弹性力学基本方程；第 2部分，杆和杆系的若干问题，包括曲梁、圆环、弹性基础梁、格排梁 (grillage)等；第3部分，薄板理论；第4部分，薄壳理论.本课程以板、壳理论为主，是一学年的课程.张教授未指定教材，但建议了很多参考书，主要有Biezeno Grammel的《Technical Dynamics》(德文本，当时尚无英译本),Timoshenko的《Theory of Plates and Shells》等.张教授还展示了一些当代大型薄壳结构工程的照片，如德国菜比锡以薄壳结构为顶盖的大型市场的照片，市场净空很大，中间没有支柱.张教授对课程的介绍，引起听课人的很大兴趣，使他们对讲课充满期待.至于这门课程为什么称为 “高等材料力学”，张维教授没有作解释，听课的人对此颇有议论，认为它是一门较深的力学理论课程，把它列入“材料力学”类课程，似乎降低了它的“理论水平”.

“高等材料力学”的第一部分是“弹性力学基本方程”.弹性力学是数学物理的一部分，其建立和早期的发展，与工程没有关联.建立弹性力学基本方程，除对弹性固体作 2个基本假设 ——“连续性假设”和“完全弹性假设”外，不作其他工作假设.在此基础上，运用力学定律，采用严密的数学方法，推导出弹性力学基本方程.张维教授讲授完这部分内容后指出：弹性力学基本方程共 15个 ——3个静力平衡方程，6个变形几何方程，6个物理方程(应力--应变关系).理论上说，基本方程普遍适用于弹性力学问题，这15个方程可求解弹性力学问题的15个未知量——3个位移分量，6个应力分量，6个应变分量.但是由于基本方程的复杂性和数学方法的局限性，采用严密的数学方法、从基本方程出发直接求解弹性力学问题，只能解少量的、物体几何形状及其受力情况都比较简单的问题，如平面问题，直杆的弯曲、扭转问题，圆柱壳、球壳问题等等.而大量工程实践中提出的固体力学问题，由于物体的几何形状及其受力的复杂性，还不能从弹性力学基本方程出发、采用严密的数学方法、直接求得问题的解——“精确解”.因此，对于这些问题，力学家们针对问题的特点，采取适当的方法，简化该问题的基本方程，使方程求解比较容易，得出的解比较简洁，便于工程应用，且有足够的精度，有人称这种解为“工程解”.本课程第二、三、四部分讨论的问题，都是近代工程实践中提出的一些固体力学问题的“工程解”.张维教授就这样把讲课内容引向第二、三、四部分，它们是本课程的主体部分.

随着讲授内容的逐步展开，听课者认识到这门课程叫 “高等材料力学”是恰当的，是有深刻意义的.材料力学课程的主要内容是讨论直杆的轴向拉伸/压缩，圆轴的扭转，直梁的弯曲和受压直杆的稳定性等问题.解这些问题，首先都是根据对物体受力后变形现象的观察，经过深入分析，作出有关变形的假设，使讨论的问题适当简化，然后运用力学定律、结合数学方法，建立所讨论问题的基本方程并求解，得出计算公式.按照这样的方法得出的材料力学计算公式，都比较简洁，便于工程应用，且有足够的精度.所以材料力学公式一直沿用至今，是工程结构设计的有力工具.以直梁弯曲问题的求解为例，开始时，基于对梁弯曲现象的观察，作出假设：变形前垂直于梁轴线的横截面，变形后仍保持平面，且垂直于变形后梁的轴线，这就是著名的“平截面假设”.在这个假设基础上，建立梁在横向载荷作用下弯曲的基本方程[1]为

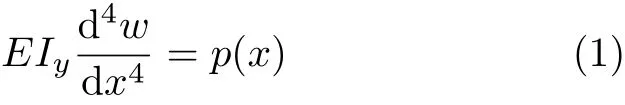
横截面上弯矩的计算公式为

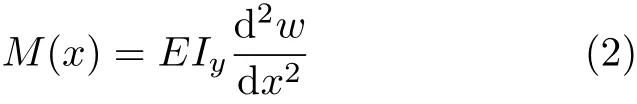
横截面上正应力的计算公式为

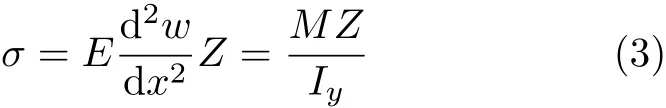
“高等材料力学”课程第二、三、四部分处理问题的方法与材料力学处理问题的方法相同，现以薄板弯曲问题为例.首先，根据对板受力后变形现象的观察作出假设：变形前垂直于板中面的直线，变形后仍保持直线，且垂直于板弯曲后的中面，即所谓“直法线假设”.在此假设基础上建立的横向分布载荷作用下薄板弯曲的基本方程[2]为

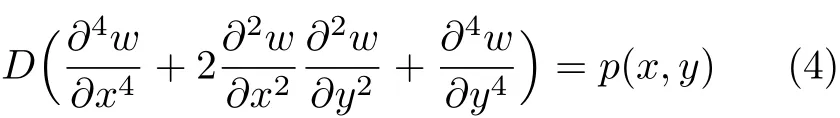
横截面上单位长度的弯矩、扭矩公式为

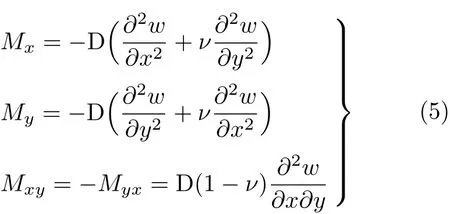
横截面上正应力和切应力的计算公式为

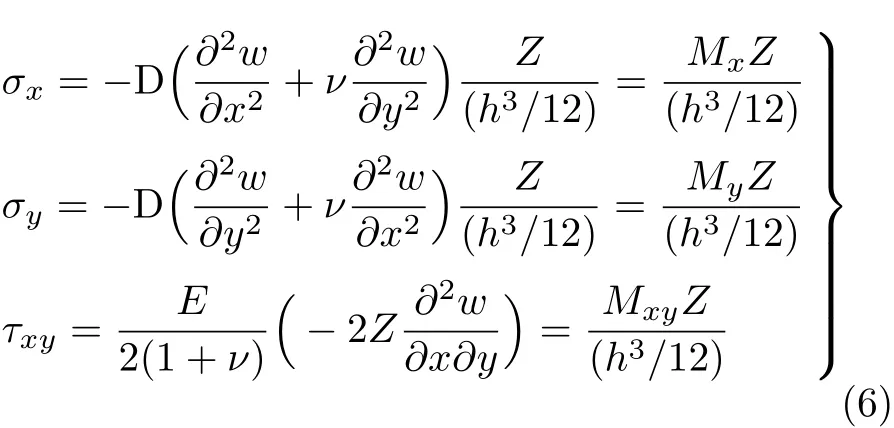
式(4)～式(6)分别与式(1)～式(3)相似，这是由于2个问题性质相同，解问题的方法相同，只不过薄板弯曲问题是二维问题，而梁的弯曲问题是一维问题，比较简单.

“高等材料力学”课程的主体部分，即第二、三、四部分讨论的问题，都是工程实践中提出的固体力学问题，主要是20世纪初以来，船舶工程、航空工程有关钢船结构、全金属飞机结构设计中提出的板壳力学问题.针对这些问题的特点，力学家在求解时采取有别于经典弹性力学处理问题的方法，而采用与材料力学处理问题一脉相承的方法.力学家基于对所研究对象 (如薄板)受力后变形现象的深入观察,区分现象的主要因素、次要因素，对变形作合理的假设，吸收一切主要因素，略去次要因素，建立模型.模型是 “一个思想上的结构物”，是 “把现象简化了的东西”[3].然后运用力学定律、结合数学方法进行分析，建立所研究问题的基本方程，并采取适当的数学方法求解.由此得出的计算公式比较简洁，便于工程应用，且有足够的精度.20世纪初以来，力学家采取这样的方法，解决了大量从工程实践中提出的固体力学问题，形成了“应用力学”这样一门有重要工程应用价值的学科，所以有人称这种解力学问题的方法为“应用力学方法”.可以认为，“高等材料力学”与本科材料力学讨论的问题性质相同，处理问题的方法相同，只不过讨论的对象不同，材料力学讨论的是一维问题，而“高等材料力学”讨论的是二维问题，比较复杂，要用到比较高深的数学方法.

张维教授当时开设 “高等材料力学”课程，把“应用力学”的研究成果，尤其是 20世纪初以来板壳理论的研究成果作为主要内容纳入讲课，使研究生掌握指导当代工程结构物设计的固体力学理论；更重要的是，通过对这些问题的讨论，把处理工程中提出的固体力学问题的方法——“应用力学方法”传授给研究生，使研究生有能力创造性地研究解决工程实践中将会提出的新的固体力学问题！

1郭日修.弹性力学与张量分析.北京:高等教育出版社，2003

2 Timoshenko SP,Woinowsky-Krieger S.Theory of Plates and Shells,2nd edn.New York:McGraw-Hill Book Company,1959

3钱学森.论技术科学.科学通报，1957，4

(责任编辑:胡 漫)

O34

：A

10.6052/1000-0879-17-186

本文于2017–05–24收到.

1)E-mail:xuefeib@163.com

郭日修.关于“高等材料力学”的一段史话.力学与实践,2017,39(4):427-429

Guo Rixiu.A brief history of“Advanced Mechanics of Materials”.Mechanics in Engineering,2017,39(4):427-429