抛物线壁内细杆的摩擦平衡分析

尤明庆

(河南理工大学能源科学与工程学院，河南焦作454010)

抛物线壁内细杆的摩擦平衡分析

尤明庆1)

(河南理工大学能源科学与工程学院，河南焦作454010)

细杆在抛物线壁内支承，平衡特性与杆长、倾角和摩擦因子相关.细杆在自身重力作用下可发生焦点下方的顺时针运动，焦点上方的逆时针运动以及两端同时下滑.基于端部支撑力达到摩擦锥边界的条件，可确定细杆状态为不平衡、稳定或不稳定的平衡和摩擦平衡.平衡集为具有宽度的叉式分岔.

抛物线，细杆，摩擦，稳定平衡，分岔

均质细杆支承于光滑圆锥曲线内壁，通过焦点时稳定平衡，重心轨迹为相同离心率 e的圆锥曲线，顶点在原曲线焦点而焦距变为e/2倍.若细杆较短不能通过焦点，则水平位置即重心在对称轴上为稳定平衡条件.重心的平衡集在圆锥曲线焦点处发生叉式分岔[1-2].

壁面总是具有摩擦的.摩擦力作为支承反力具有不确定性.文献[3-7]研究了不同倾角平面的两端摩擦支承直杆问题；不过，对圆锥曲线壁面的摩擦支承问题，系统参数增加到3个，即摩擦因子、离心率以及杆长与焦距的比值，使问题更复杂难解.本文仅研究离心率为1的圆锥曲线，即抛物线壁内细杆的摩擦平衡问题.

1 抛物线的几何特征

设抛物线焦距p为 1，相当于几何参数均以 p无量纲化，因而焦点至顶点距离为1/2，过焦点且垂直于对称轴的弦长为2；在直角坐标系中方程为

其内壁支承长L的细杆AB，因对称性而设细杆右侧A不低于左侧B；系统的状态参数为中点M或倾角θ，有

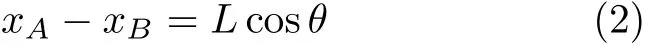
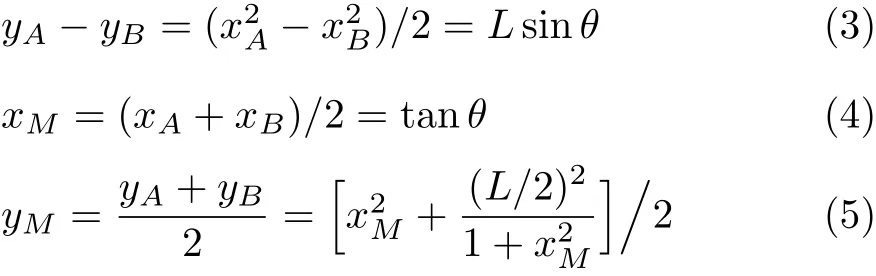
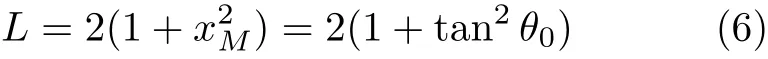
时达到极小值(图1)

因抛物线上的点到焦点 P与到准线的距离相等，细杆中点M 到准线距离就是(PA+PB)/2，则APB为直线即细杆通过焦点时重心最低[2]，相应的倾角为式(6)给出的θ0.

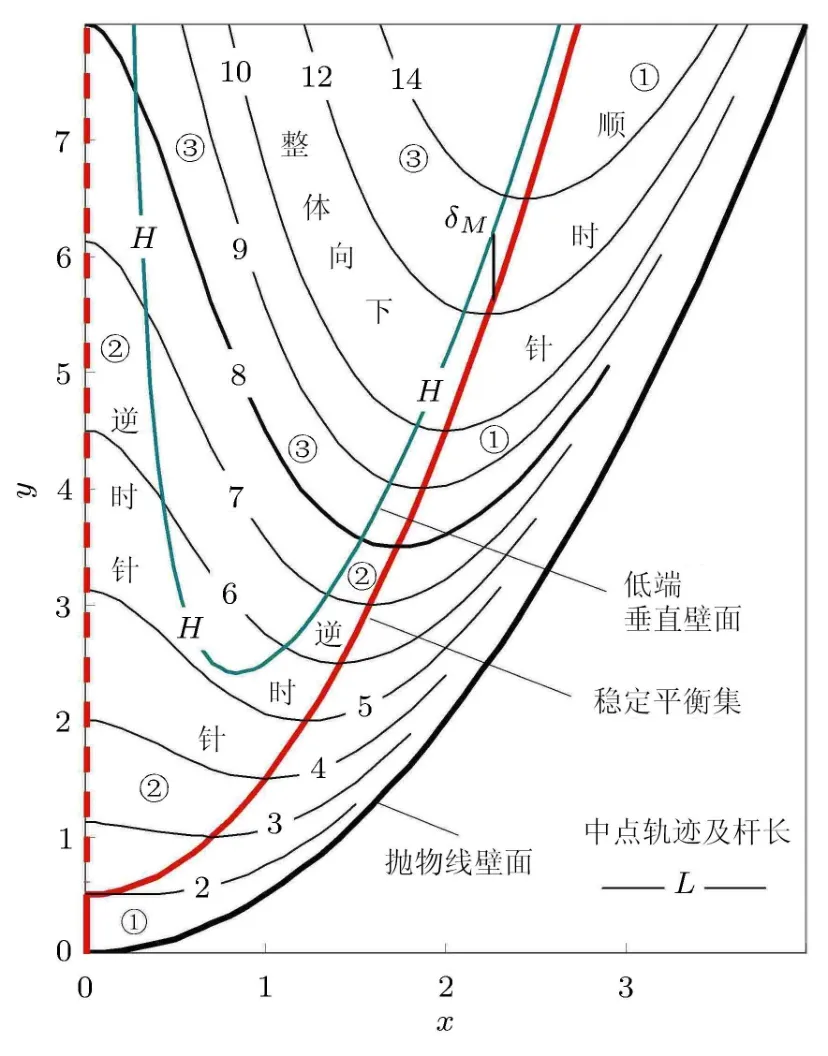
图1 细杆的运动方式和中点轨迹以及平衡集

细杆在自身重力作用下的滑动有3种情形：焦点下方的顺时针运动①，焦点上方的逆时针运动②或两端同时下滑③(图2).后者低端B处法线在细杆的下方，因而细杆与法线一致即垂直壁面是相应区域的边界H；由式(1)～式(4)得到其最小值为杆长小于 L则不存在两

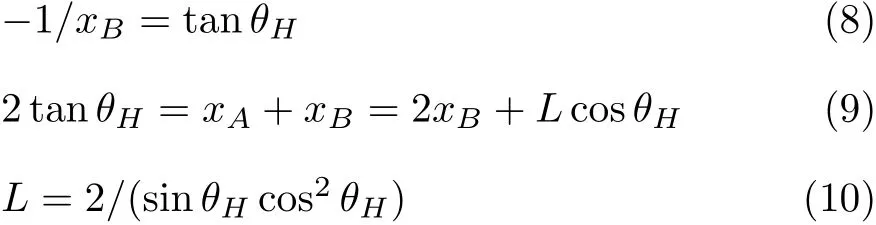
h端同时向下滑动的可能；而长度大于Lh则θH有两解.基于式(10)，以式(4)和式(5)计算相应的中点轨迹(图1)：细杆中点在表示H的该曲线上方则具有两端同时下滑的趋势.

图2给出长度L=8细杆的位置.其通过焦点时倾角θ0为60°.倾角为θH=15.65°以及56.90°时低端B垂直于壁面，而右端A则达到最高和最低点，两者之间即区域③内细杆低端与下方壁面的夹角大于90°，即使摩擦平衡，扰动也可使其失去支承而滑脱.

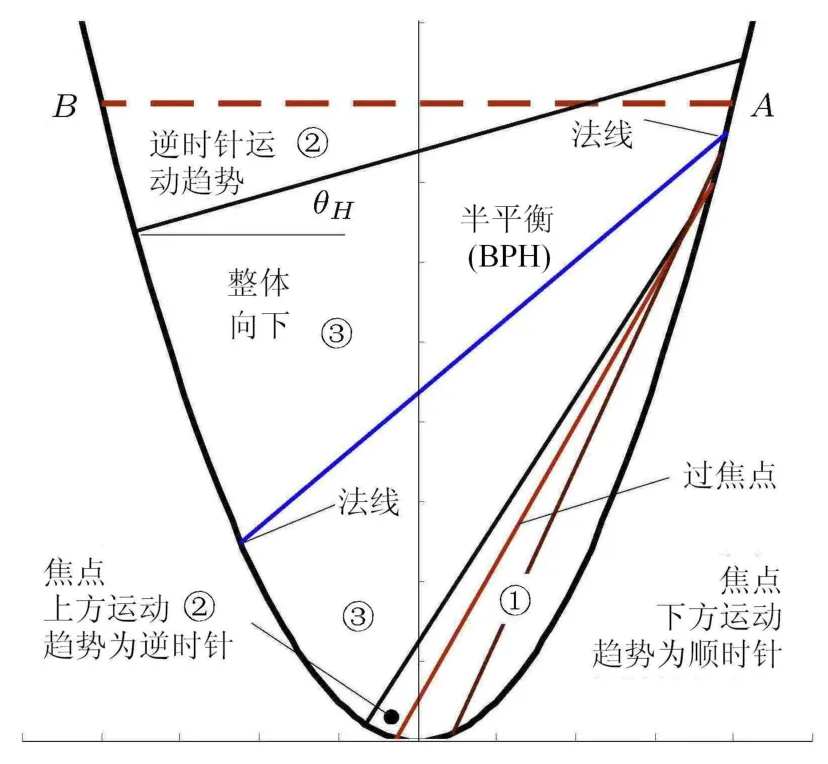
图2 L=8的细杆在抛物线壁面内的运动趋势

2 细杆摩擦支撑下的平衡

摩擦力具有不确定性，因而细杆可以在倾角一定的范围内平衡，即摩擦使平衡区域扩大.细杆两端支撑力的方向为kA和kB，其交点(x,y)满足

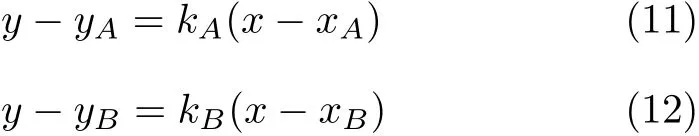
消去y求得x，平衡时应与细杆重心即中点的横坐标xM相等，利用式(1)化简可得

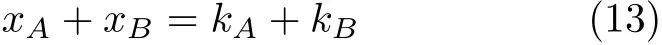
抛物线x2=2y的法线斜率为-1/x；设摩擦因子µ=tanϕ，ϕ为摩擦角，则摩擦锥左、右界的斜率为

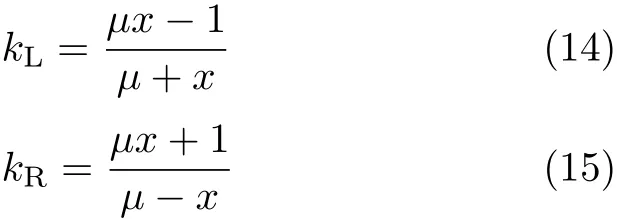
焦点下方重力滑动趋势总是逆时针 (图 1中①)，两端摩擦力达到摩擦锥右界即式 (15)时为临界平衡状态；将其代入式(13)可得

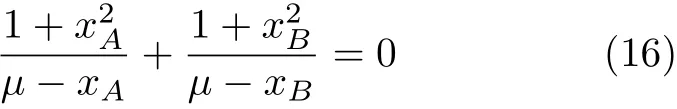
利用式(2)～式(4)可得细杆摩擦滑移发生的条件

细杆在焦点上方运动趋势若为逆时针(图1中②)，则摩擦力达到摩擦锥左界即式 (14)时临界平衡，有

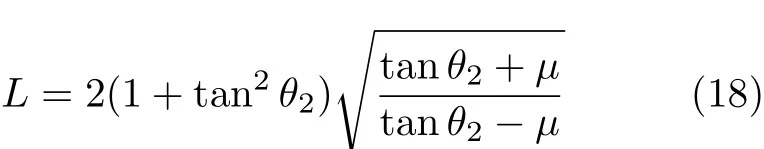
给定摩擦因子µ，式(18)在

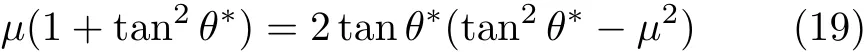
时长度达到最小值 L∗；若 L＞L∗时式 (18)有两解，对应于细杆离开水平位置及接近稳定平衡位置.实际计算时可先给定 θ∗由式 (19)确定摩擦因子µ=tanϕ，再由式 (18)计算相应的杆长 L∗；该杆长下的倾角θ0和θ1也在图3给出.摩擦角增大时临界杆长从2平稳增加，但3个特征倾角都从0°急速增加，如图3所示ϕ=2°时相应的L∗=2.444，θ1=28.9°.

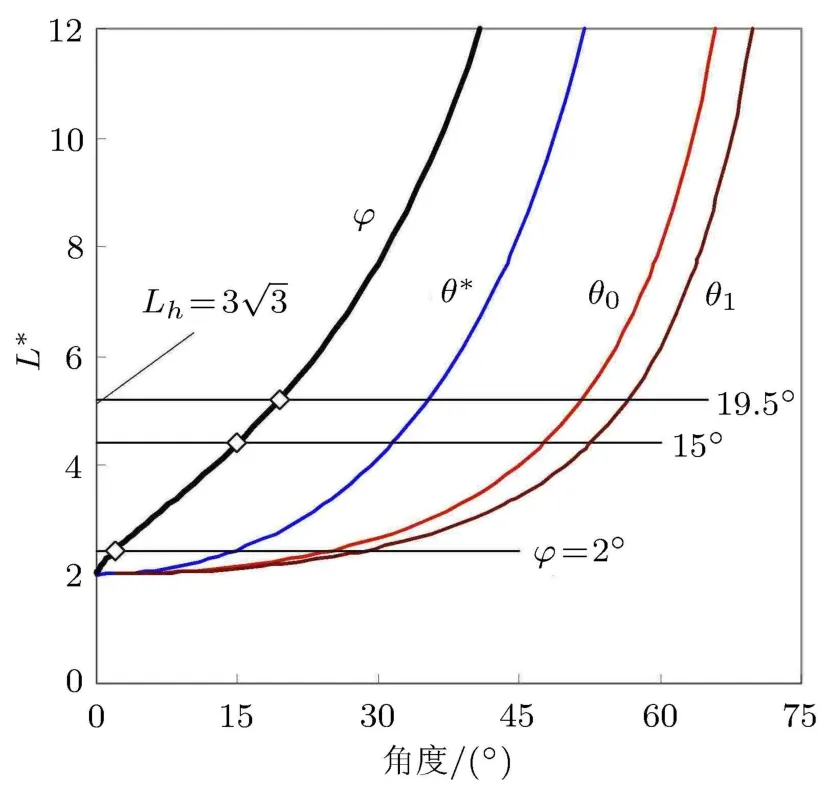
图3 临界杆长随摩擦角的变化及相关角度参数

细杆位于图1中区域③,具有整体向下运动趋势，左右两端支承力分别达到各自摩擦锥左右界时发生滑动，基于式(13)～式 (15)，并利用式(2)～式(4)可得

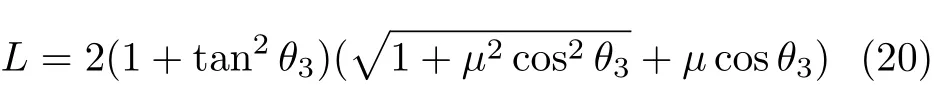
而摩擦平衡时受扰动可能失去支承而滑脱(图2).

3 平衡位置的区划

式(6)的稳定平衡集θ0、式(10)的两端下滑区边界θH与摩擦因子无关––相应的细杆中点轨迹已在图1给出，而3个滑动条件即式(17)、式(18)和式 (20)随摩擦因子而变化.图 4是摩擦角 ϕ为30°和15°时的结果.

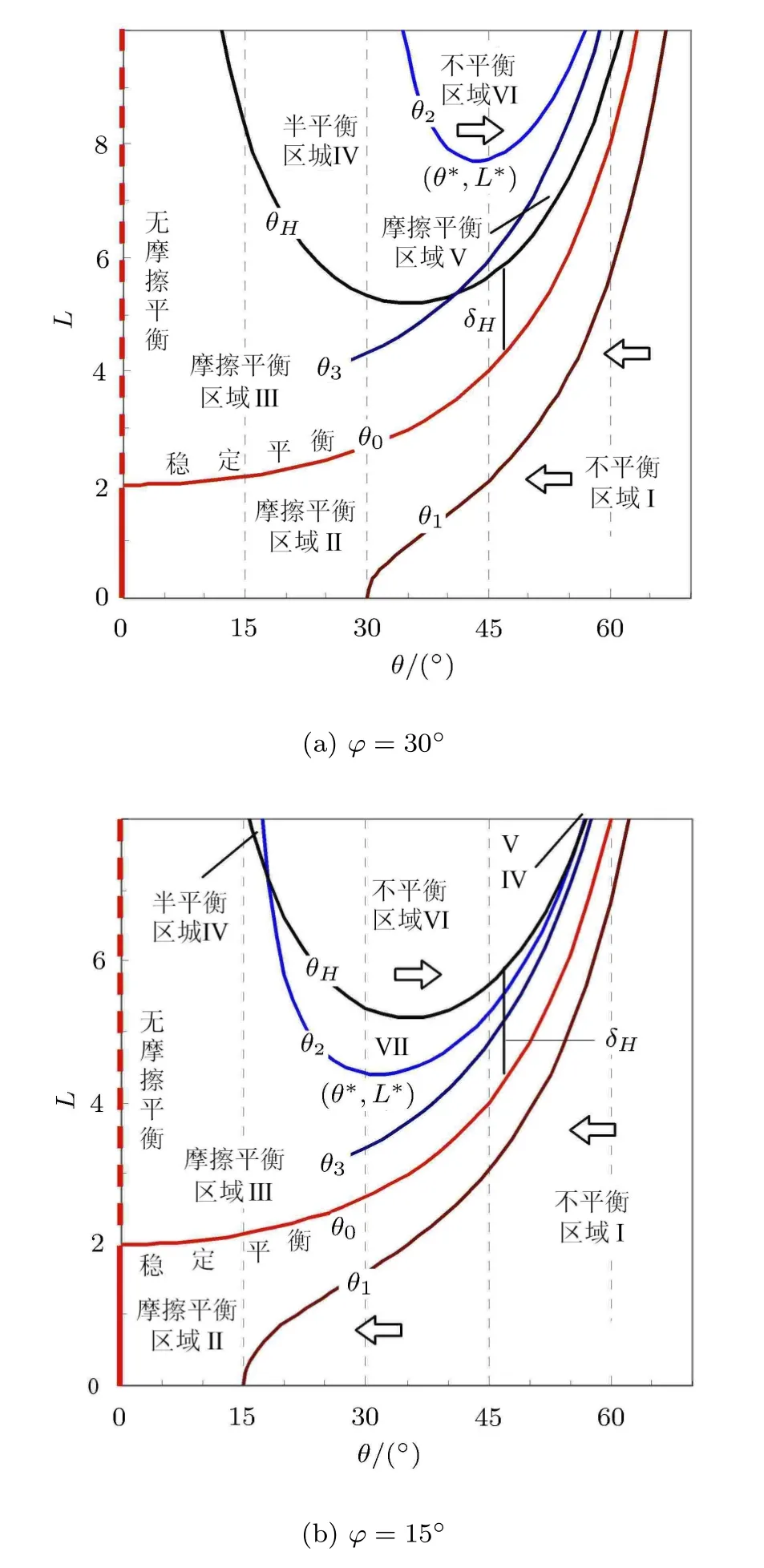
图4 细杆长度和倾角对平衡状态的影响

式 (20)确定的长度是倾角 θ3的单调递增函数，且随摩擦角的增大而增加；若细杆处于可两端同时向下运动的位置即图1和图2中③，且长度和倾角处于式 (20)曲线 θ3右下方即图 4的区域 V中，则摩擦平衡，否则重力可克服摩擦力而使杆下滑.记η=µcosθ，则

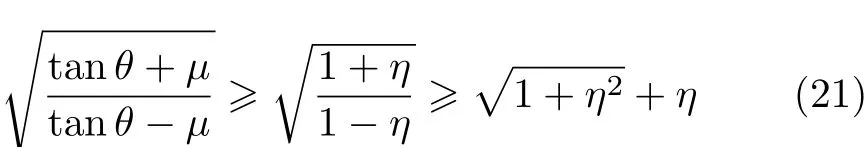
因而式(18)曲线θ2全部在式(20)曲线θ3的上方.

倾角相同且接近90°时，式(20)与式(6)对应的杆长差异，即图4中曲线θH与曲线θ0的纵坐标差异

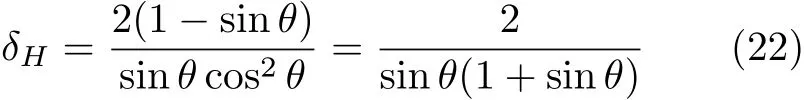
逐渐减小而趋于 1.由式 (4)和式 (5)可知，倾角相同就是中点横坐标相同，而中点纵坐标的差异δM趋于1/2(图1)；反之，长度相同时，对应角度θH与θ0的差异以及角度正切即中点横坐标的差异都会趋于0.

注意到θ趋于90°即cosθ趋于0时有

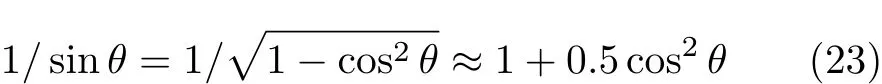
因而只要摩擦因子不为零，相同倾角θ且接近90°时式(10)一定小于式(20)，即曲线θH最终在曲线θ3的下方而趋于曲线θ0，两者构成摩擦平衡区域V.图4(b)中ϕ=15°的区域V在L=10.2后出现.

由式(10),式(18)及式(20)可得曲线θH与曲线θ2及曲线θ3的交点

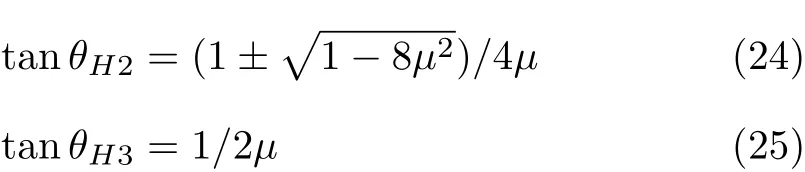
图 5给出摩擦角对交点位置的影响.ϕ=15°时，曲线θH与曲线θ2及曲线θ3在图4(b)右上角之外的交点对应的细杆长度为8.05和10.2.显然，θH趋于0和θ2趋于ϕ都对应于杆长趋于无穷，因而杆长充分大之后，图4中曲线从左向右按θH,θ2, θ2,θ3,θH,θ0,θ1排列.

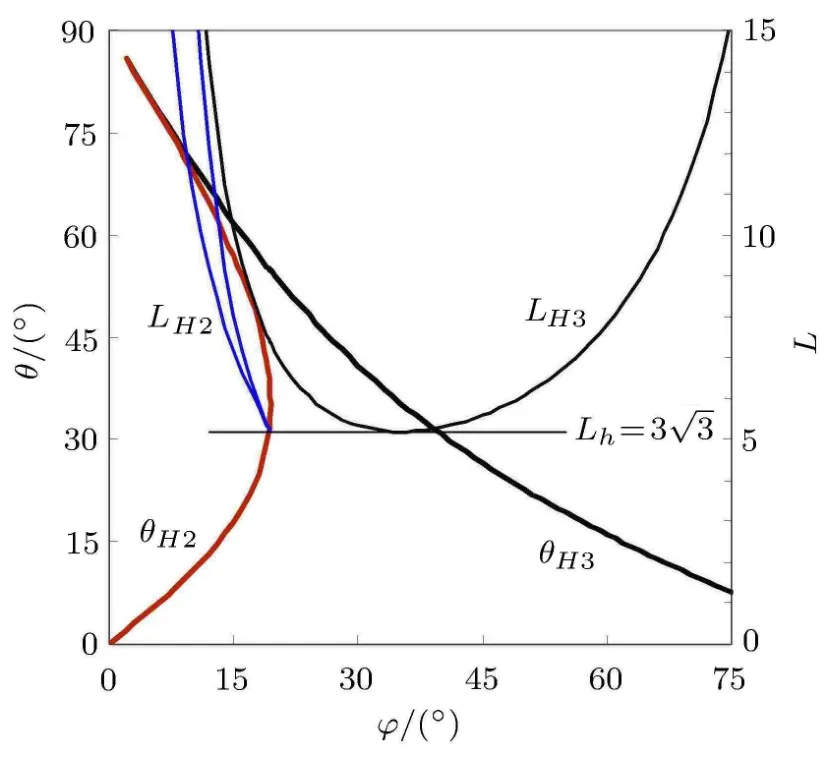
图5 细杆长度和倾角对平衡状态的影响

4 稳定性和极限状态的讨论

通常所说的系统稳定是指所受扰动消失之后仍能回复到原来的状态.不过，摩擦支承的细杆平衡状态，受扰后的实际状态却与扰动相关而具有不确定性.因此细杆稳定只是意味着微小扰动将引起状态的微小改变；而引起突变的扰动大小对应于稳定性的高低.下面参照细杆中点位置对平衡状态的稳定特征进行具体说明.

4.1 ϕ＞ϕ∗=19.5°

图6给出ϕ=30°时由细杆中点位置表征的平衡状态，标示符号与图4(a)相对应.细杆处于焦点即曲线θ0右下侧时，以曲线θ1分为不平衡区域Ⅰ或摩擦平衡区域Ⅱ.曲线θ2上方是不平衡区域Ⅵ；曲线θH整体在曲线θ2下方，其与θ0之间的区域Ⅲ是逆时针运动趋势的摩擦平衡.摩擦角增大，不平衡区域Ⅰ和Ⅵ缩小，即图6中不平衡的边界①右移，边界②上抬.

细杆在θ2,θH及θ3之间的区域Ⅳ，不能依靠摩擦而避免两端同时下滑.不过，若先放置低端B并阻止滑动后再放置高端 A(实际操作时可稍稍下压)，细杆也可在 A端向下、B端向上的摩擦作用下平衡，如图2中BPH，以下称之为半平衡；但扰动之后下端就会失去支承，即摩擦平衡是不稳定的.又，这里不考虑细杆弹性压缩而产生的附加正压力以及摩擦力[6-8].

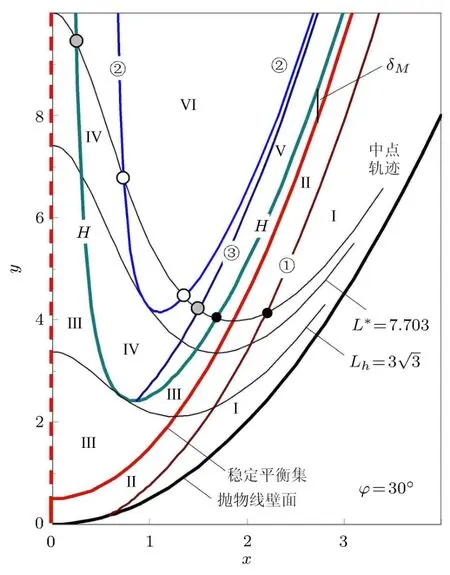
图6 摩擦角ϕ=30°时细杆中点位置的平衡状态区划

4.2 ϕ≤ϕ∗=19.5°

摩擦角ϕ减小时，摩擦平衡界限的曲线θ1向稳定平衡集θ0靠近；曲线θ2和曲线θ3随ϕ减小而下移，在即摩擦角低于ϕ∗=19.5°之后，曲线θ2达到曲线θH下方，如图4(b)所示，不平衡区域Ⅵ扩大而分割区域Ⅳ成左右两部分；曲线θ3也随之下降，其与曲线θH在L=10.2相交后构成区域Ⅴ.

图7给出ϕ=15°时细杆平衡的中点位置区划.右上部，细杆低端垂直于壁面的曲线H与曲线②、③相交，三者界定的是半平衡区域Ⅳ，曲线H与③之间是平衡区域V.两者都是不稳定的摩擦平衡.曲线 H与②界定的区域Ⅶ是细杆逆时针运动的不平衡，上方区域Ⅵ则是两端下滑的不平衡区域.其余与图6类似.

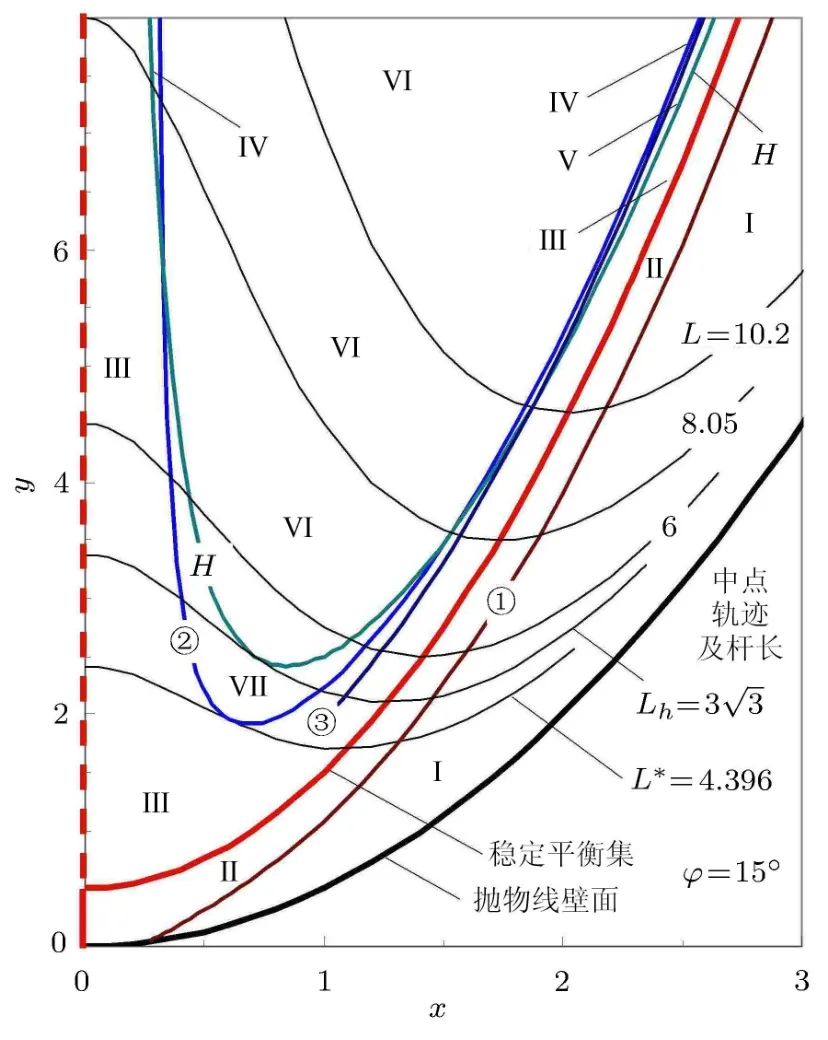
图7 摩擦角ϕ=15°时细杆中点位置的平衡状态区划

细杆在水平状态附近摩擦平衡，扰动较大则可能进入不平衡区域，而稳定平衡集附近的摩擦平衡总是稳定的.此外，若扰动具有周期性，如振动或热胀冷缩，将驱使细杆重心最终达到最低值，即无摩擦时的稳定平衡位置.相关计算和分析可参阅文献[7,9].

4.3 杆长趋于无限

抛物线壁面光滑时，细杆中心的平衡集在焦点处发生叉式分岔，而摩擦使“叉”具有了宽度.给定摩擦因子 µ=tanϕ时，由式 (18)可知倾角 θ2趋于ϕ即杆长趋于无限时,细杆中点xM=tanθ趋于摩擦因子µ.随高度增加抛物线壁面趋陡，杆长趋于无限时倾角 θH趋于 0.因此对称轴处中叉宽度趋于2µ，但稳定的摩擦平衡区域Ⅲ逐渐收窄变尖(图6和图7).

另一方面，θ1→90°时式(17)可写为

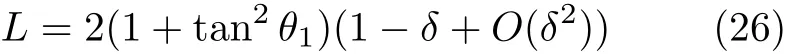
式中δ=µ/tanθ1为小量；再利用式(6)，有

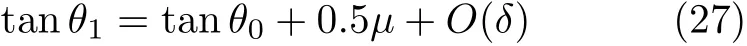
同样，基于式(18)和式(20)可得到

如前所述，杆长 L趋于无穷时 tanθH趋于tanθ0，因而稳定的摩擦平衡区域Ⅲ将变尖，不稳定的平衡区域Ⅴ则随之增大(图6和图7).式(27)～式(29)意味着，杆长趋于无穷时摩擦平衡边界与过焦点稳定平衡处的中点横坐标xM=tanθ的差异趋于±0.5µ，即平衡区域的外叉宽度趋于µ=tanϕ，且右侧稳定平衡区域Ⅱ和左侧不稳定平衡区域V各占其半.

4.4 摩擦因子趋于零

图8给出摩擦角ϕ为0.5°～15°的不平衡区域边界①和②处细杆中点轨迹，两端同时下滑的位置③未达到图中范围.显然，ϕ趋于零时不平衡区域的界限即式(17)的θ1曲线和式(18)的θ2曲线从两侧趋于无摩擦时稳定和不稳定的平衡位置；不过，ϕ=0°时两式及式(20)都蜕化为式(6)，即只有细杆过焦点而不含有水平姿态的平衡状态.

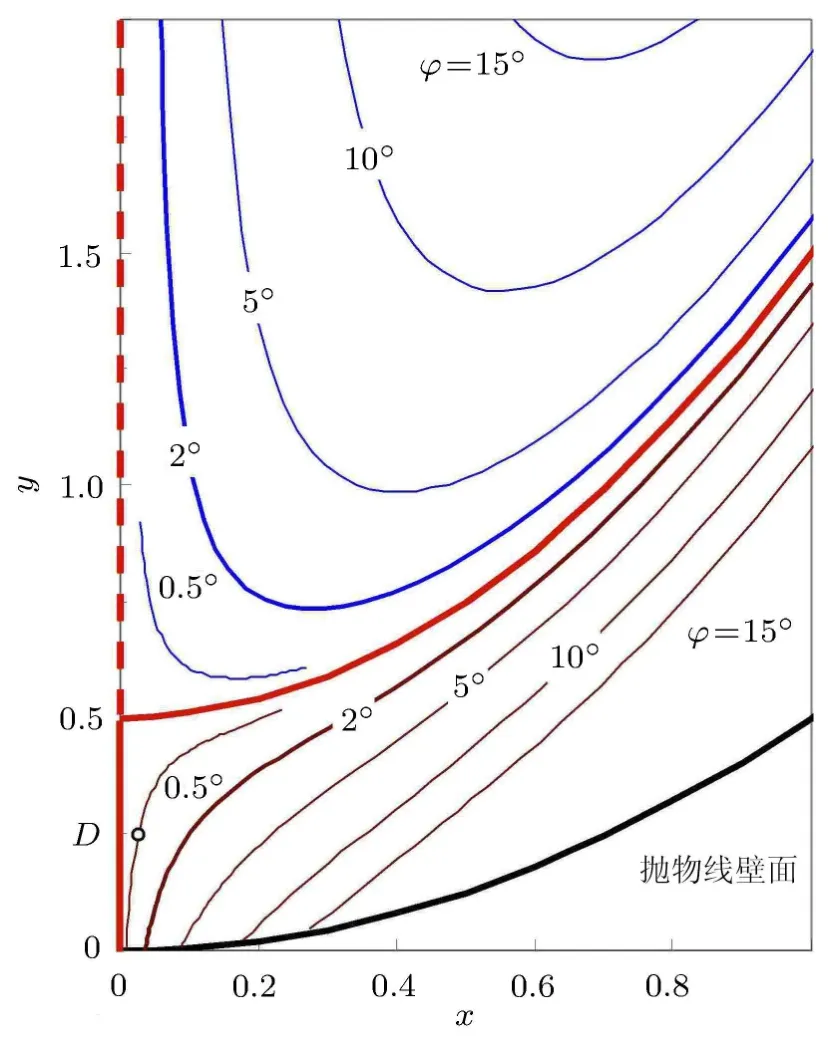
图8 不同摩擦角下不平衡区域边界处的细杆中点轨迹

细杆长度趋于零时极限平衡处抛物线切线的斜率就是摩擦因子µ.ϕ在5°以下，焦点下方的平衡边界开始外凸，向稳定平衡集趋近.ϕ=0.5°时，图8中的D点相应于倾角θ=3ϕ；若式(17)中保持θ=3ϕ不变而ϕ趋于0，则D点趋于对称轴上y=1/4处，杆长趋于.更为一般地说，摩擦角ϕ为无穷小而非零时，式(17)中L在0～2之间、式(18)中L在2～∞之间的倾角θ都是无穷小，但ϕ为零时式(17)、式(18)中根号项变为1就不再含有相关信息.

当然，绝对光滑的界面实际上并不存在，而ϕ= 2°即 µ=0.035已接近常见固体界面的下限[10]；基于图3计算结果，长度L∗=2.444的细杆在倾角±28.9°之内均可获得稳定的摩擦平衡.

5 结语

抛物线壁面光滑时，细杆中心的平衡集在焦点处发生叉式分岔，而摩擦使“叉”具有了宽度.因杆长、倾角和摩擦系数不同，细杆可具有不平衡、稳定或不稳定的平衡和摩擦平衡等多种状态.

1徐康.圆锥曲线的静力学性质.力学与实践，2014,36(5):639-641

2尤明庆.均匀细杆在光滑圆锥曲线壁内的稳定平衡分析.力学与实践，2016,38(2):186-188

3 Gonzalez AG,Gratton J.Reaction forces on a ladder leaning on a rough wall.American Journal of Physics,1996, 64(8):1001-1005

4丁文镜，曾杰，樊世超.有摩擦斜梯平衡问题的非静定性.工程力学，2000，17(5):32-36

5 Bennett J,Mauney A.The static ladder problem with two sources of friction.The Physics Teacher,2011,49(12):567-569

6肖化燚,谢建华.重杆在墙角间的平衡问题.力学与实践,2013, 35(1):89-92

7尤明庆.摩擦作用下直杆在对称斜面间的稳定平衡分析.力学季刊，2016,37(2):381-388

8薛纭，刘昭.受圆柱面约束弹性细杆的摩擦平衡分析.力学季刊，2016,37(1):139-148

9尤明庆. 周期扰动引起的物体单向运动.力学与实践，2010, 32(4):117-118

10 https://en.wikipedia.org/wiki/Friction

(责任编辑:刘希国)

STABLE EQUILIBRIUM OF A POLE ON A FRICTIONAL PARABOLA WALL

YOU Mingqing1)
(School of Energy Science and Engineering,Henan Polytechnic University,Jiaozuo,454010,China)

The equilibrium of a pole supported on a parabola wall is related to its length,slope angle and the frictional factor between them.Under the action of gravity,the pole can move clockwise under the focus of parabola,and move counterclockwise or slide down at two ends over the focus.The state of pole,i.e. disequilibrium,stable and unstable equilibrium with friction,is determined on the support force at the boundary of friction cone.The equilibrium set is a pitchfork bifurcation with width related to the frictional factor.

parabola wall,pole,friction,stable equilibrium,bifurcation

O317

：Adoi：10.6052/1000-0879-17-102

2017–03–27收到第1稿，2017–05–19收到修改稿.

1)E-mail:youmq@hpu.edu.cn

尤明庆.抛物线壁内细杆的摩擦平衡分析.力学与实践,2017,39(4):359-364

You Mingqing.Stable equilibrium of a pole on a frictional parabola wall.Mechanics in Engineering,2017,39(4): 359-364