组合杆件扭转实验设计与课程教学实践1)
2017-09-11马文江尚新春
张 憬 马文江 尚新春
∗(北京科技大学自然科学基础实验中心,北京100083)
†(北京科技大学数理学院应用力学系,北京100083)
组合杆件扭转实验设计与课程教学实践1)
张 憬∗,2)马文江∗尚新春†
∗(北京科技大学自然科学基础实验中心,北京100083)
†(北京科技大学数理学院应用力学系,北京100083)
设计制作了一种比较复杂的弯扭组合变形结构作为实验装置.基于材料力学空间杆件的弯扭组合变形的强度计算,确定施加扭矩载荷的弹性极限值.对该装置进行了两组扭转实验测试,测试结果和理论计算结果比较表明,二者吻合较好.本实验是对材料力学实验改革的有益尝试,可直接应用于材料力学实验教学中.
教学改革,组合杆件,扭转实验
在传统的材料力学实验教学中,扭转实验通常用单个金属圆杆作为试件[1],笔者曾尝试过用双金属材料复合圆杆为试件,对传统的单轴扭转实验进行了扩展,并用于实验教学[2].目前,弯扭组合变形实验则多采用圆管加外伸臂的实验装置[34],目的是使学生对一维杆件组合变形的空间受力平衡和强度理论等内容有更直观的认识,并且学习复杂应力状态的应力测量方法.为了丰富组合变形的实验课程内容,设计了一种组合杆扭转实验装置[5],相对于圆筒加外伸臂实验装置,其受力和变形情况更为复杂,所涵盖的力学基础知识还涉及到了弹性结构的静不定问题.多次教学实践表明,组合杆扭转实验可以引导学生应用所学相关力学理论知识及基本实验技能,对较为复杂条件下的材料力学性能和结构变形进行测试,有利于培养他们的动手能力.
1 实验装置的设计与理论计算
1.1 实验装置
设计出的组合杆扭转实验装置由2个圆盘,6根圆杆以及夹持端组成,如图1所示.每根圆杆长度l=150mm,截面直径D=6mm.圆盘上有6个圆孔,其中心在正六边形的顶角上,距圆盘圆心的距离均为R=40mm.每根杆与圆盘以螺栓方式连接,可拆卸组装成两杆、三杆、四杆、六杆扭转装置.另外,与扭转机夹具相联的夹持端焊接在圆盘中心处,即扭转机的主扭转力矩T作用于圆盘中心轴线上.

图1 多杆扭转实验装置
1.2 装置结构的组合变形分析
以三杆组合扭转为例,其理论分析和实验方法可推广到 n杆扭转装置.在圆盘外力偶 T的作用下,相互平行且等距的3个圆杆处于平衡状态,其横截面上的受力情况是相同的(见图2).
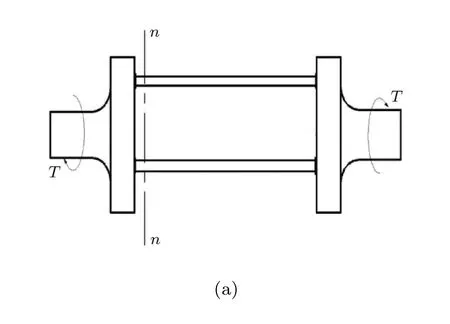
图2 三杆扭转装置
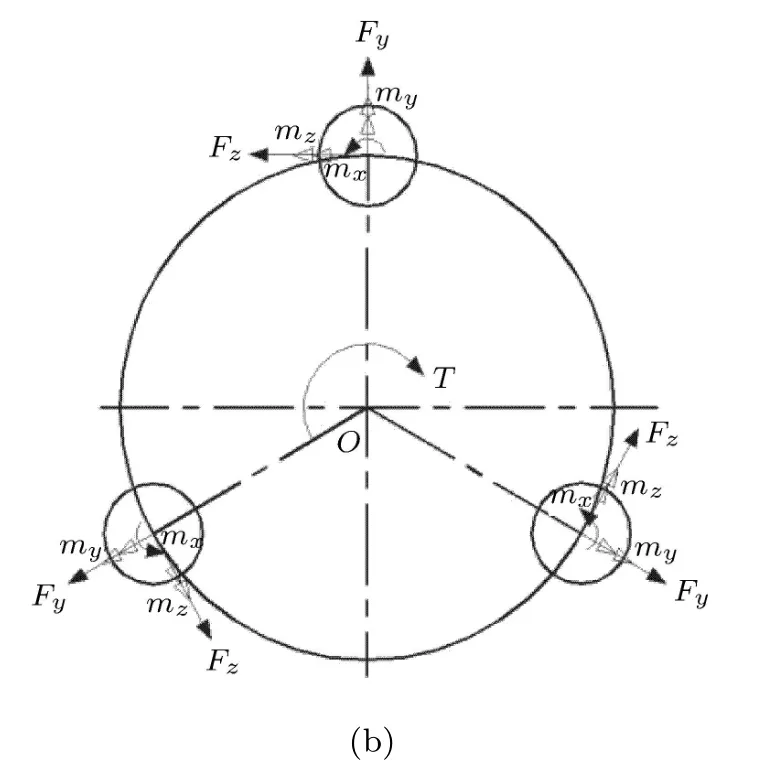
图2 三杆扭转装置(续)
建立Oxyz坐标系,其原点取在圆杆一端面的圆心处,圆杆的轴线为x轴.在每个圆杆的n-n截面上均有3个内力Fx,Fy,Fz和3个力偶mx,my, mz(见图3(a)).由空间力系的平衡方程ΣFx=0可知Fx=0,再由ΣMx=0可得
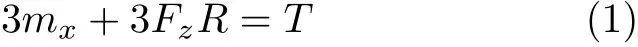

图3 单个圆杆的横截面上的内力和转角
其余的4个平衡方程是自动满足的.方程(1)含有两个未知量Fz和mx,因而需要求解静不定问题.
现在来建立相应的变形协调关系.利用对称性,可仅对任一圆杆进行变形分析.由于刚体圆盘扭转时始终在同一平面内转动,圆杆的两端与圆盘以螺栓方式连接,因此圆杆的两端可视为完全固定约束.这样,杆的端截面绕y轴的转角θy和绕z轴的转角θz均为零.再由弹性悬臂梁的组合变形理论可知自由端的转角和z方向的挠度分别为[6]

式中,E为拉伸弹性模量,I为惯性矩.
圆杆由扭矩 mx产生的扭转角为 α = mxl/GIP(其中IP为圆杆截面的极惯性矩,G为杆材料的剪切模量).由图3(b)可知,它与圆盘的刚体转动角ϕ之间的关系为ϕ=α,并且挠度vz与转角ϕ之间满足vz=Rϕ,再由式(2)的第3式可得
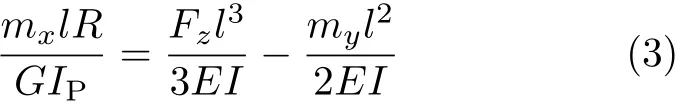
此外,由于各圆杆中心与圆盘中心之间的距离不变,故圆杆在y方向上的挠度为零
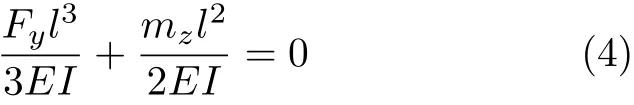
可由式(1)~式(4)解出Fy=0和mz=0,以及非零的约束反力
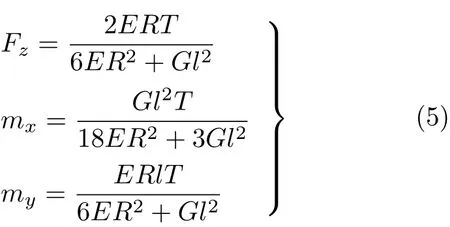
危险截面上的弯曲正应力和扭转切应力分别为
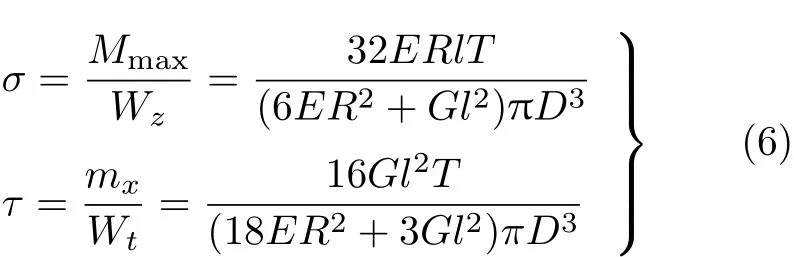
其中,Wz和Wt分别为圆杆的抗弯和抗扭截面模量.
同理,可推导出在n杆组合扭转装置的危险截面上弯曲正应力和扭转切应力分别为

1.3 极限扭矩载荷的计算
圆弹性杆材料为 Q235钢,屈服强度 σs= 235MPa,杨氏模量E=200GPa,剪切模量G= 80GPa.取安全因子 ns=2,则许用载荷 [σ]= σs/ns=117.5MPa.再由式(6)和第四强度理论计算可得T≤Tmax=7.09N·m.
1.4 实验载荷下圆盘转角的理论计算
由上述分析可得中圆盘刚体转动角的计算公式为
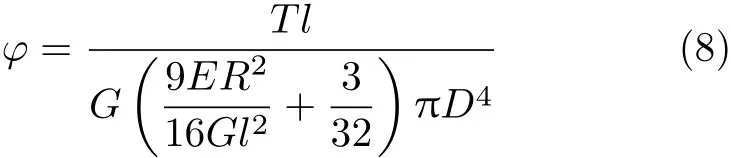
当T=4N·m和T=5N·m时,分别有ϕ=0.54°和ϕ=0.68°.当T=Tmax=7.09N·m时,ϕ=0.965°.
2 实验的实施与结果比较
采用电测法来测量三杆的危险点主应力大小,将三杆分别编号1,2,3号,在每根杆近端处的上表面粘贴0°-45°-90°应变花,按照1/4桥接法来组桥.使用扭转试验机来施加4N·m和5N·m载荷,各应变片的应变值通过静态应变仪显示出来.将测试值代入
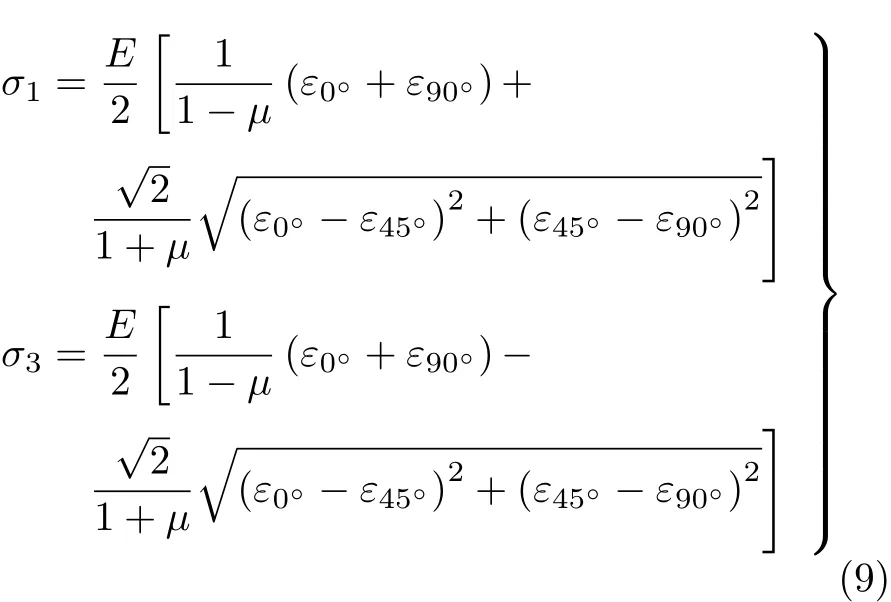
得到所测点的主应力大小,列于表1中.
由表1实验值与理论值对比可知,两者存在一定的相对误差.引起误差的原因可能有两个方面:一是在实验中被测点的位置只能是靠近理论确定的危险点,应变片的定位、粘贴时胶水的厚度、导线电阻、被测试样的安装等原因可能会影响实验测试的结果;二是理论计算是基于一维杆件的弹性理论,并将杆和圆盘的连接处理成固定端,这些都是实际情况的理想化近似.
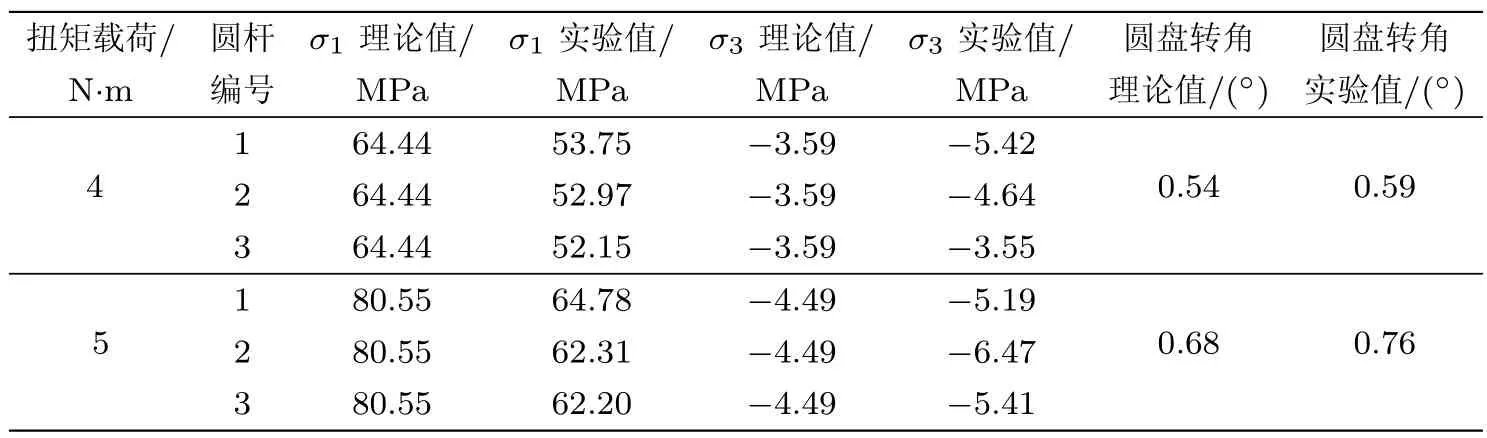
表1 主应力理论值和实测值
3 组合杆扭转实验的教学实践
弯扭组合变形实验一直以来是高校材料力学实验教学中一个重要的综合性实验.如何设计新颖的实验来丰富教学内容并激发学生对实验课的学习兴趣,是当前实验课程教学改革探讨的新问题.对此,通过组合杆扭转实验,将新的教学内容引入实际的实验课程中.课前让学生结合所学材料力学有关内容,学习相关参考文献,分析杆件的受力情况,并求出实验的许用扭矩;在实验课上让学生应用电测法对组合杆组合结构进行应变测试.实验课后让学生进行主应力的理论值计算,并与其实验值比较,最后写出分析结果和完整的实验报告.
组合杆扭转的教学实践取得了很好的效果,首先,它所涉及的内容是对静不定杆件结构的内力分析、强度理论、叠加原理等知识点的综合运用,是对传统的材料力学实验和理论教学内容的延伸和扩展.学生通过此实验可以运用已掌握的基本知识来解决更为复杂的问题,不仅对课本内容有了更深层次的理解,更开拓了思维,提高了他们分析解决问题的能力.其次,在工程实际中,许多构件往往存在这样的组合变形,掌握对较为复杂条件下的材料力学性能和结构变形的测试方法,有助于学生的学习更贴合工程实际,提高其工程实践意识;第三,实验测试结合理论计算来进行比较,培养了学生严谨的科学态度,通过对结果的分析讨论,提高了学生的科研分析能力.此组合杆扭转实验的教学实践,丰富了教学内容,是对材料力学实验改革的有益尝试,具有很好的推广应用价值.
1古滨.材料力学实验指导与实验基本训练.北京:北京理工大学出版社,2011
2张憬,马文江,尚新春.材料力学扭转实验的扩展和探讨.实验技术与管理,2014,31(7):209-211
3付朝华,胡德贵,蒋小林.材料力学实验.北京:清华大学出版社,2010
4朱鋐庆,彭华,林树等.材料力学实验.武汉:武汉大学出版社, 2006
5尚新春,肖久梅,马文江等.工科力学的教学与课外科技活动实践//2009力学课程报告论坛论文集.北京:高等教育出版社, 2010
6刘鸿文.材料力学(上册).北京:高等教育出版社,2004
(责任编辑:胡 漫)
O341
:A
10.6052/1000-0879-17-058
2017–02–24收到第1稿,2017–05–14收到修改稿.
1)北京科技大学教育教学改革项目“适应卓越工程师培养的力学实验教学改革与探索”(JG2013M57)、“面向卓越计划人才培养体系的力学实验教学项目的研究与探索”(JG2015M56)资助.
2)张憬,工学硕士,工程师,从事实验力学教学及研究工作.E-mail:0811zhangjing@ustb.edu.cn
张憬,马文江,尚新春.组合杆件扭转实验设计与课程教学实践.力学与实践,2017,39(4):389-392
Zhang Jing,Ma Wenjiang,Shang Xinchun.Design and teaching practice for the torsion experiment of multi-rods structure.Mechanics in Engineering,2017,39(4):389-392
