人体--结构系统的水平振动实验1)

刘 祥 叶 茂 曹文斌

(广州大学--淡江大学工程结构灾害与控制联合研究中心,广州510006)

人体
--结构系统的水平振动实验1)

刘 祥2)叶 茂 曹文斌

(广州大学--淡江大学工程结构灾害与控制联合研究中心,广州510006)

针对静止状态人对结构水平振动特性的影响，建立实验平台，分别测试并分析了质量块--结构系统、单人--结构系统、多人--结构系统水平自振频率与阻尼比变化规律.给出了两种人--结构系统静态水平耦合模型的比较分析以及人体的水平振动频率估计.结果表明：在分析静止状态下人对结构水平振动特性的影响时，人体不可简单作为质量块或质量--弹簧--阻尼系统，而应看作带人体刚性质量的质量--弹簧--阻尼系统.结合实验测试数据和人--结构系统水平耦合模型，得到人体水平前后向频率范围为0.236～3.748Hz，人体水平左右向频率范围为0.194～5.32Hz.

人--结构，质量块--结构，振动测试，模态分析

现代建筑结构体系趋向轻质化、长大化，导致了结构自振频率越来越小，从而使得人--结构相互作用越来越明显，严重时还会导致结构产生共振破坏，国内外有许多类似这方面报道[12].另一方面，作用在结构上的人体本身是一个复杂的系统，人与结构显著的相互作用使得人--结构系统更加复杂.

目前，国内外学者对人与结构系统竖向的相互耦合作用研究比较多.在国外，Griffin[3]最早对人体竖向的振动特性进行数值模拟分析，建立了人体有限元模型，通过实验计算获得了人体竖向振动频率大约在5～7Hz左右.Zhang等[46]对人体竖向振动模型做了大量研究，建立了两质量单自由度离散人体竖向振动模型、两自由度离散人体竖向振动模型、连续分布人体竖向振动模型，并且开展了理论分析和实验研究，与传统的人体振动模型以及其他学者建立的人体振动模型相比，他们的实验模型有了明显的改进.国内许多科研人员[713]也分别建立了人--结构竖向耦合系统模型，并进行耦合动力特性分析.

国内外学者关于人与结构相互作用的研究主要集中于竖向耦合的情况，而对人--结构系统水平耦合的情况研究却比较少.然而实际情况却是，临时搭建的看台等结构由于人的作用产生水平共振而导致坍塌的危害很大，有必要开展对人--结构系统水平耦合振动的研究.为此，本文基于实验，提出了两种人--结构水平自振耦合系统模型，结合实验研究，对两种模型进行分析对比，得到合理的人--结构水平向振动系统模型，最终得到了人体水平向振动频率范围，为相关工程设计提供参考.

1 实验概要

实验采用 Q345钢组合而成的钢平台模型，高为1.21m、长宽为0.6m×0.6m.4根柱子和8根横梁为长0.05m，宽0.03m，厚2mm的矩形钢管.平台模型平面钢板厚为0.01m.支座处采用螺钉锚固.同时为了研究方便，定义钢柱横截面短边为水平 x向，长边为水平y向，高为z向.如图1所示.

在实验过程中，采用了丹麦B&K 3560D噪声与振动信号采集分析系统，其中4个B&K4381加速度计用来采集加速度信号，1个B&K2692型放大器用来控制信号大小，1个B&K3050模块采集数据.测点布置在平台对角上横梁处.

实验首先对空平台结构进行自由振动测试，随后进行了质量块 -结构系统、单人--结构系统、多人--结构系统水平自振测试试验，对比质量块--结构系统和人体质量与质量块相近的单人--结构系统的自振频率，分析试验结果并总结了静态人体对平台结构水平振动特性的影响.

图1 实验模型

2 质量块--结构系统

经过实验测试可得，平台结构水平第一阶模态为x向，频率为12.54Hz，阻尼比为1.242%；水平第二阶模态为y向，频率为18.72Hz，阻尼比为1.099%.

同时通过不断在平台结构上加载质量块的方式测试分析质量块对平台结构水平振动特性的影响，平台结构上加载的质量块，材质是混凝土试块，6次加载的试块质量分别为 15kg,29.2kg,42.8kg, 56.2kg,68.9kg,83.9kg，加载次数编号为T1，T2，T3，T4，T5，T6.

表1列出了6次加载下质量块--平台系统前两阶水平频率值和阻尼比值.利用表中实测数据计算得到了平台结构水平第一阶模态质量为 36.04kg，刚度为223521，阻尼为70.5；平台结构水平第二阶模态质量为35.48kg，刚度为490362，阻尼为84.2.

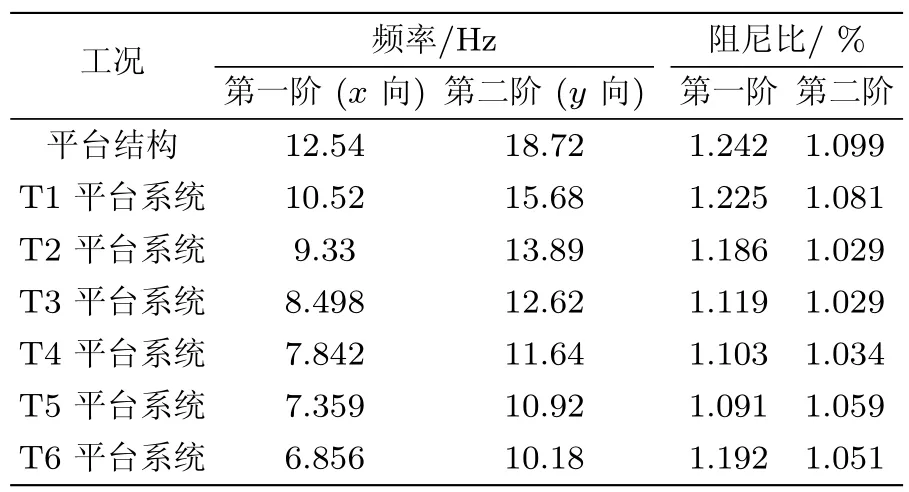
表1 不同质量块--平台系统实测的模态变化

同时，基于空平台结构测试数据，将平台结构在两个方向上分别简化为单自由度系统，质量块作为质量附加在单自由度系统上，计算不同质量块--结构系统前两阶水平自振频率，如图2所示，从图中看到两个方向水平自振频率实测值与模拟值吻合较好.针对人--结构水平耦合系统中人体是否能作为质量块的问题，也将人作为质量块附加在单自由度结构系统上进行计算.

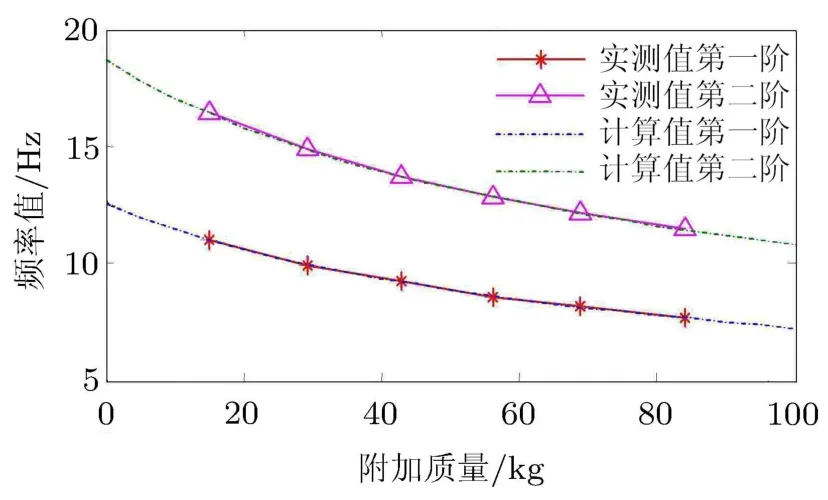
图2 质量块--结构系统频率随重量的变化规律

表 2列出了人--结构系统在两个水平方向振动频率的实测值与计算值.可以看到，在单人--结构系统中，实测的第一阶水平自振频率与计算模拟值间的误差达到29.64%，比质量相近的T3结构系统实测第一阶水平自振频率与计算模拟值之间的误差 (0.23%)大得多；此外，单人--结构系统中实测的第二阶水平自振频率与计算模拟值间的误差达到了30.67%，远远大于质量相近的T3--结构系统中实测的第二阶水平自振频率与计算模拟值之间的误差(0.13%).

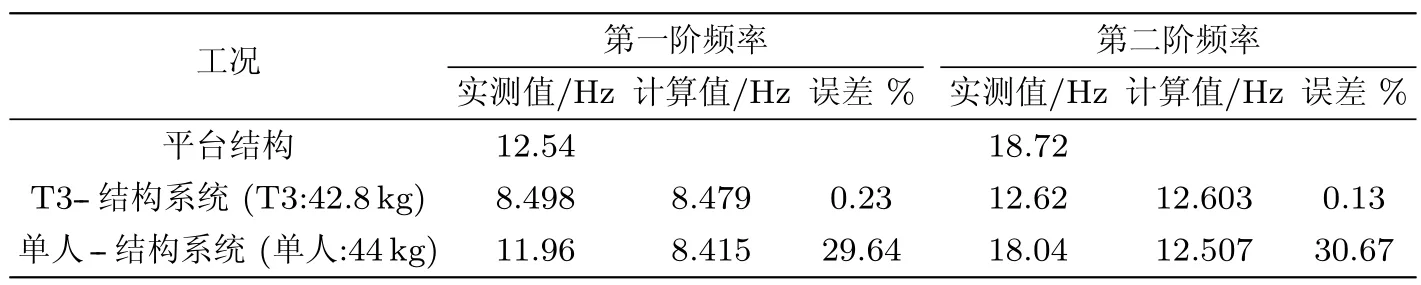
表2 实测频率与计算频率对比

相对平台结构前两阶水平自振频率，单人--结构系统实测自振频率值略下降：第一阶下降0.58Hz，第二阶下降0.68Hz，自振频率减小值远小于相近质量的T3--结构系统实测自振频率相对平台结构水平自振频率的减小值.

研究表明，在探究静止状态下人对结构水平振动特性的影响时，不可简单地将人体看作为质量块.

3 单人、双人、三人--结构系统实验

实验对3人编号为P1,P2,P3.分别开展包括单人静止站立，双人静止站立，3人静止站立下人--结构系统水平振动特性研究，实验中人都面朝x正方向站立.

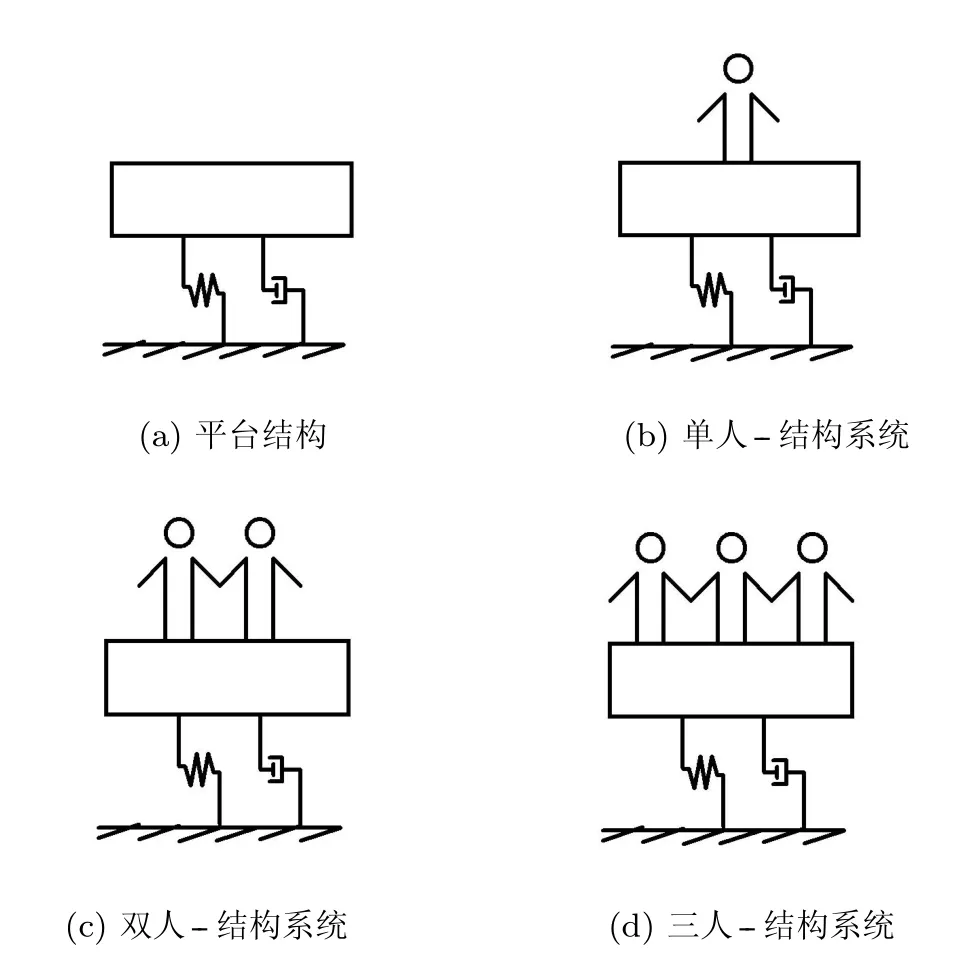
图3 平台结构、单人、双人、三人--平台系统示意图

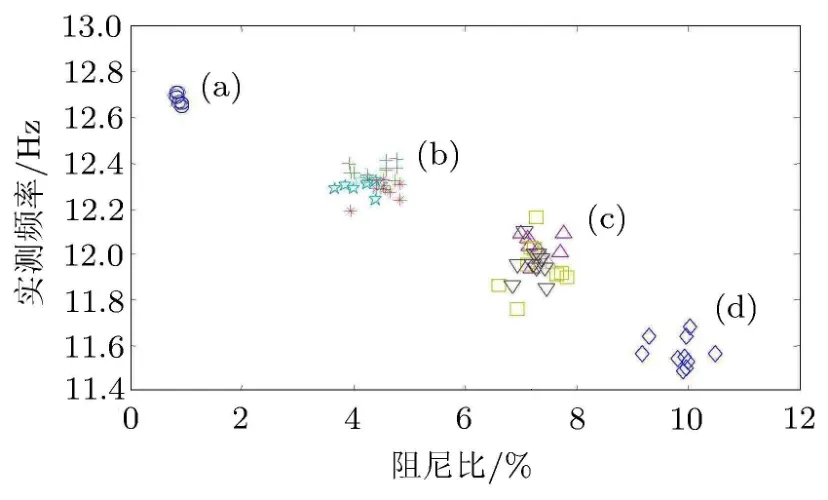
图4 实测4种系统第一阶频率与阻尼比分布

图3为平台结构、单人--结构系统、双人--结构系统、3人--结构系统示意图，对应图4中(a)～(d).图4表示在4种不同系统下，测试得到的水平自由振动频率与阻尼比的分布.从图4中可以看出，随着平台结构上人数的增加，频率小幅度下降，下降幅值在0.2～0.3Hz左右，同时阻尼比明显增大，说明人群大小对结构体系有显著的阻尼效果，从而提出单人--结构水平静态耦合系统模型A和B，如图5所示.需要说明的是：(1)人体结构的复杂性，导致了从图4中看到平台上人数增加时测得的数据比空平台结构数据分散性大；(2)实验平台结构的水平自振频率较高，远大于人体水平自振频率[14].实测中测得的结构频率为单人--结构系统的第二阶频率，该频率和平台结构的水平自振频率接近，同时单人--结构系统的第一阶频率无法直接从平台结构上测得的，而此频率更接近于人体的水平自振频率[15].

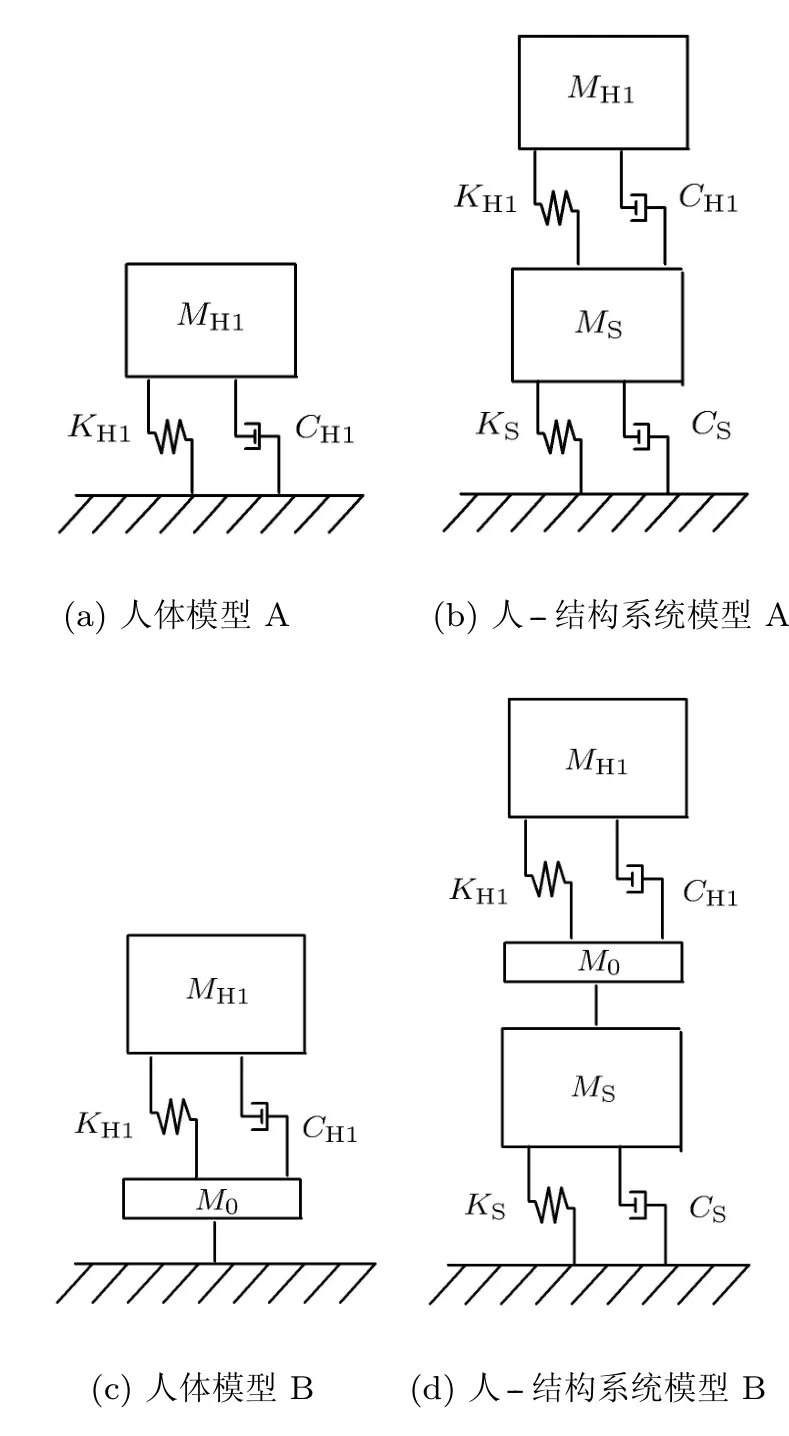
图5 两种人--结构系统模型

4 单人--结构系统模型

由实验现象把单人作为单自由度质量--弹簧--阻尼系统，建立水平向的人体--结构模型.如图5(a)和图5(b)所示，人体模型A是一个有阻尼单自由度系统，与平台结构构成人--结构系统模型A.此外,人体生物动力学研究提出人体刚性质量的概念[7]，即将人体的质量分解成刚性质量M0和振动质量MH1两部分，前者相当于在人与结构相接处加上一个与结构相接点的位移保持一致的质量块，后者可相对结构振动，建立人体模型B，如图5(c)和图(d)所示，与平台结构构成人--结构系统模型B.

4.1 人--结构系统水平振动方程

(1)人--结构系统模型A

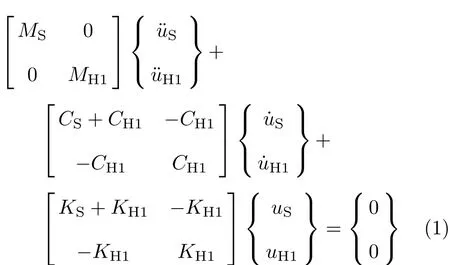
(2)人--结构系统模型B

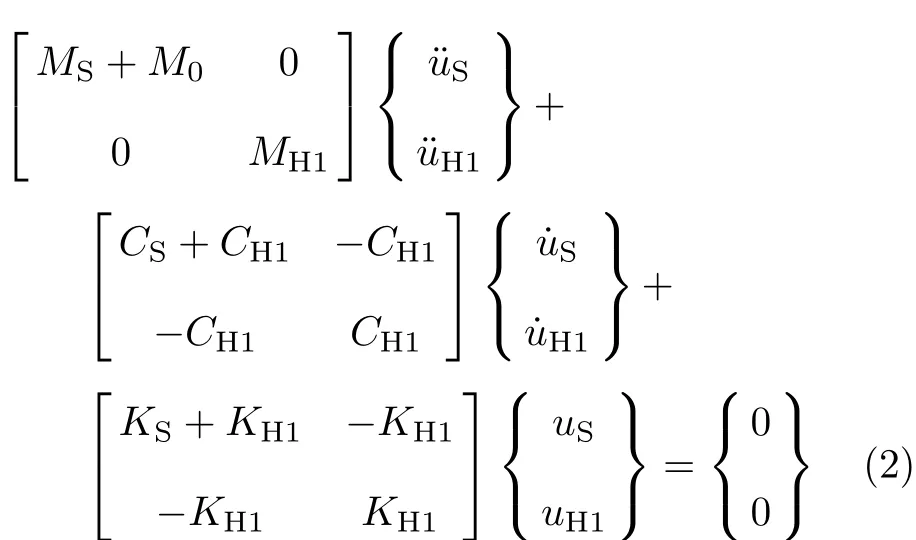
式中

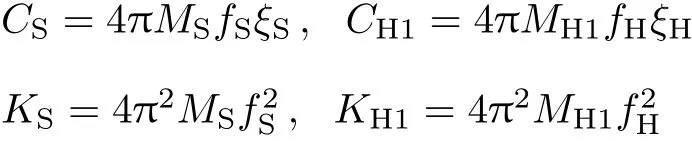
MS为平台结构水平模态质量，CS为平台结构水平模态阻尼，KS为平台结构水平模态刚度，fS为平台结构水平频率，ξS为平台结构水平阻尼比；MH1为人体水平模态质量，CH1为人体水平模态阻尼，KH1为人体水平模态刚度，fH为人体水平频率，ξH为人体水平阻尼比；M0为人体刚性质量.

随着平台上人数的增加，自由度也随之增加，因此该力学模型仅适用于单人--结构系统构成的两自由度水平振动系统.

4.2 人--结构系统模型

由无阻尼特征方程可以推导得人 --结构系统模型前两阶水平向频率与结构水平自振频率之比f1/f，f2/f.

e为人体刚性质量与人体总质量之比，η为人体质量与结构水平模态质量之比，β为人体固有自振频率与结构自振频率之比.图6分别表示η为10%、50%、100%、140%、200%时，人--结构系统模型A和人--结构系统模型B的第二阶水平自振频率随β变化规律,其中e取10%[16].

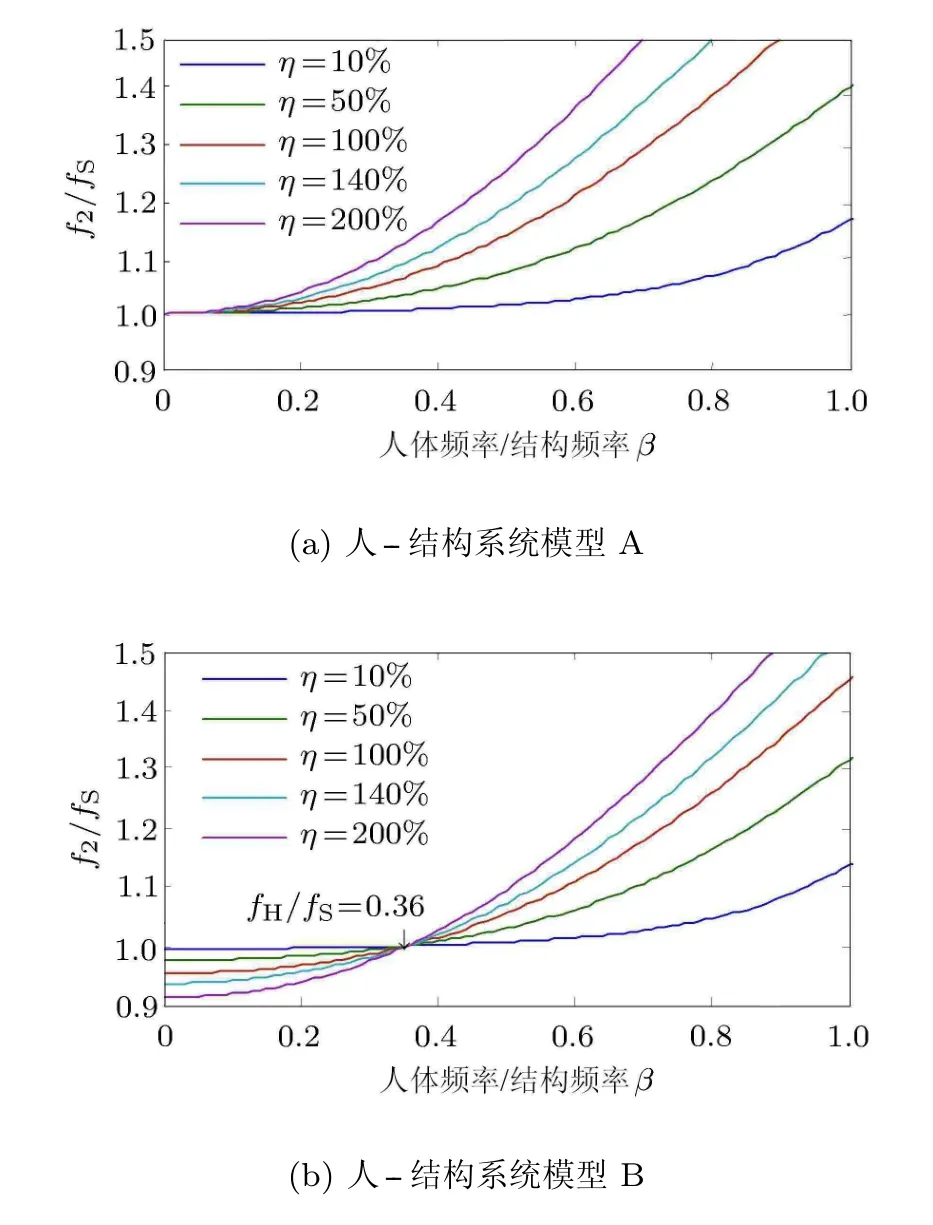
图6 人--结构系统f2/fS随β变化图

从图6(a)中得出,当η不变时f2/fS随fH/fS升高而上升，并且f2/fS在不同η下都大于1，说明人--结构模型A中第二阶频率大于结构频率，并且随着人体质量增加而增大，f2/fS随fH/fS的升高速率而变大，说明当人--结构模型A中第二阶随人体质量增大时，上升越明显.

从图6(b)中得出,当η不变时f2/fS随fH/fS升高而上升，但是在fH/fS＜0.36区间内f2/fS＜1.同时当η=10%时，f2/fS在fH/fS＜0.36区间内接近于 1，当 η＞10%且 fH/fS＜0.36时，0.9＜f2/fS＜1.说明随着人体质量的增加，人--结构模型B中第二阶频率在fH/fS＜0.36区间内小于结构第一阶频率.实验测得质量为67.3kg的人静止站立平台结构是频率值为12.11Hz，小于平台结构第一阶频率12.54Hz，并且0.9＜12.11/12.54=0.966＜1.与人--结构系统模型A相比，人--结构系统模型B与实测现象更吻合，说明人--结构模型B更合理.

综上所述，人体刚性质量对人--结构系统水平自振频率是有影响的，实验中出现人--结构系统自振频率降低的现象一方面是由人体刚性质量引起的，另一方面人体阻尼也会有一定贡献[4].主导因素仍需更进一步研究.

4.3 人体水平频率范围

由式(2)得人体水平频率为

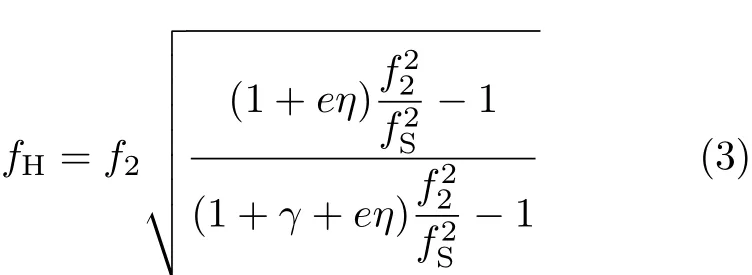
本次实验测试多人站立下的人--结构系统自振频率值.测试人员共40人，面朝x向静止站立，年龄介乎24～30之间，体重在44～97kg之间，男女比例为4:1，基本代表国内中青年人群.设e为10%[16]，根据式(3)计算人体水平频率，图7描绘了40人的水平前后向和左右向的自振频率分布图，由图中可得，人体水平前后向的频率值在0.236Hz至3.748Hz之间，平均值为2.48Hz；人体水平左右向的频率值在0.194Hz至5.32Hz之间，平均值为3.55Hz.

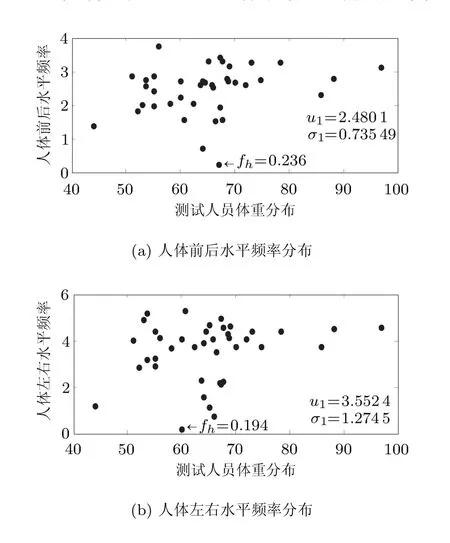
图7 人体水平频率分布(实验测试40人)

Matsumoto等[14]对共12个人进行人体水平频率测试，得到人体水平前后向频率大约为0.125Hz，人体水平左右向频率大约为0.5Hz.由于人体的复杂性为实验探索增加了很多不确定因素，Matsumoto等[14]对人体的直接测试仍处在探索阶段. 本文通过间接测试得到的人体水平频率值与Matsumoto等[14]直接测得的值存在一定差异.

综上所述，通过实验与理论相结合的方法得到人体水平前后向频率范围为0.236～3.748Hz，人体水平左右向频率范围为0.194～5.32Hz.由于测试中人员身高、体重、站立姿势等因素不同，导致人体水平频率存在差异.

5 结论

针对人静止状态下人--结构系统水平振动特性研究，提出了两种人--结构水平自振耦合系统模型.并给出了人体水平振动频率估计，主要结论如下：

(1)通过实验的方法对比相近质量块--结构系统前两阶频率值和人静止站立下单人--结构系统前两阶水平自振频率，表明单人静止站立时亦不可简单作为质量块.

(2)实验测试单人静止站立、多人静止站立下人--结构系统水平自振频率与阻尼比，得到以下结论：增加平台结构上测试人员的数量，人--结构系统的水平自振频率会有所减小，减小值在 0.2～0.3Hz左右.与此同时，系统的阻尼比反而会变大，说明人对结构有阻尼影响.

(3)根据实验现象提出人--结构的两个系统模型A、B，由理论研究得到，两个系统模型第二阶水平自振频率都随β升高而升高，但在人--结构系统模型B中，把人体看作刚性质量，当η大于50%，β小于0.36时，人--结构系统第二阶频率小于结构第一阶频率，基本与实验现象相符合，从而说明，与人--结构系统模型A相比，带人体刚性质量的人--结构模型B更合理.

(4)实验测试了40人静止站立下人--结构系统水平自由振动频率值，通过理论计算得到人体水平前后向频率范围为0.236～3.748Hz，人体水平左右向频率范围为0.194～5.32Hz.

1《广州日报》.王菲演唱会观众席垮塌.http://gzdaily.dayoo. com/html/2012-02/18/content-1615291.htm.2012.2.18.01.

2《广州日报》.瑞典一音乐会看台坍塌.http://gzdaily.dayoo. com/html/2012-03/04/content-1630714.htm.2012.3.4.A8.

3 Griffin MJ.Handbook of Human Vibration.New York: Academic Press,1990

4 Zhang QW.Models of a standing human body in structural vibration.Structures&Buildings,2013,166(7):367-378

5 Zhang Q,Ji T.Representation of a standing human body in vertical vibration.The 45th UK Conference on Human response to Vibration.2010,12:6-8

6 Zhou D,Ji T.Free vibration of rectangular plates with attached discrete sprung masses.Shock and Vibration,2012, 19(1):101-112

7陈建英，方之楚.人--结构相互作用动力学建模研究.振动与冲击，2007,26(6):10-13

8王海,周叮,王曙光.人--梁相互作用动力学模型研究.工程力学,2010,27(5):14-20

9何浩祥，闫维明，张爱林.竖向环境振动下人与结构相互作用及舒适度研究.振动工程学报，2008,21(5):446-451

10秦敬伟,杨庆山,杨娜.人体--结构系统静态耦合的模态参数.振动与冲击,2012,31(15):150-157

11杨予,杨云芳,洪震,胡杰云,蔡其茅.人体站姿竖向振动等效单自由度模型参数研究.振动与冲击,2012,36(23):154-157

12何卫，谢伟平，刘隆.人--板耦合系统动力特性研究.工程力学, 2013,30(1):295-300

13刘隆,谢伟平,徐薇.均布人群对简支欧拉梁动力特性的影响.工程力学,2012,29(8):189-194

14 Matsumoto Y,Griffin MJ.The horizontal apparent mass of the standing human body.Journal of Sound and Vibration,2011,330(13):3284-3297

15 Ellis BR.Human-structure interaction in vertical vibrations.Proceedings of the ICE-Structures and Buildings, 1997,122(1):1-9

16 Sachse R.The inf l uences of human occupants on the dynamic properties of slender structures.[PhD Thesis].England:University of Sheffield,2002

(责任编辑:胡 漫)

EXPERIMENTAL STUDY OF LATERAL VIBRATION OF HUMAN-STRUCTURE SYSTEM1)

LIU Xiang2)YE MaoCAO Wenbin
(Tamkang University-Guangzhou University Joint Research Center for Engineering Structure,Guangzhou University, Guangzhou 510006,China)

To study the impact of human body in the stationary state on the lateral vibration performance of structure,an experimental platform is built up and the horizontal natural frequency of the vibration and the damping ratio of the mass-structure system and the human-structure systems are tested and analyzed. Two static lateral coupling models of the human-structure system are used,to obtain the range of the lateral vibration frequency of human body.It is shown that the human body in the stationary state could not be simplif i ed as a mass block as in a mass-springs-damping system to evaluate the impact of the human body on the lateral vibration performance of the structure,and a mass-spring-damper system should be adopted with the human body as a rigid mass.Based on the experimental data and the human-structure coupling model,the ranges of the lateral frequency and the fore-and-aft frequency of the human are calculated,with the results of 0.236～3.748Hz and 0.194～5.32Hz,respectively.

human-structure,mass-structure,vibration measurement,modal analysis

TU317+.1；O327

：Adoi：10.6052/1000-0879-16-428

2016–12–28收到第1稿，2017–04–30收到修改稿.

1)国家自然科学基金(51178126,51208125)、广州市科技计划项目(2013J2200074)和广东省科技计划(2016B050501004)资助项目.

2)E-mail:360259069@qq.com

刘祥,叶茂,曹文斌.人体--结构系统的水平振动实验.力学与实践,2017,39(4):365-370

Liu Xiang,Ye Mao,Cao Wenbin.Experimental study of lateral vibration of human-structure system.Mechanics in Engineering,2017,39(4):365-370