旅客需求双向转移的列车客票收益联合优化问题
2017-09-11李杲岭彭其渊
李杲岭 彭其渊
(西南交通大学交通运输与物流学院 成都 610031)
旅客需求双向转移的列车客票收益联合优化问题
李杲岭 彭其渊
(西南交通大学交通运输与物流学院 成都 610031)
考虑铁路不同客运产品之间的替代性影响,将旅客双向转移行嵌入单条线路、多区段、两种不同客运产品的客票联合优化问题中.以高速列车一等座和二等座为例,在旅客向上和向下购买概率已知的条件下,以各OD区间两种席位的预订限制票额为决策变量,以整体收益最大为目标,建立了一个带约束的非线性整数规划模型,并利用线性规划与粒子群算法相结合的方法对模型进行求解.算例结果表明,旅客不同的选择行为对最优决策及整体收益具有不同程度的影响,对于任意一种转移行为而言,随着转移概率的增加,期望总收益逐渐增大.
替代性影响;联合优化;预订限制;期望总收益
0 引 言
目前我国铁路客票大多采用单一的票价模式,从“多路段、单票价”的角度,利用席位控制策略解决铁路客运收益管理问题具有现实意义.从收益管理研究对象(资源或产品)的个数来看,收益管理模型可分为单维收益管理模型和网络收益管理模型;而从控制策略来说,动态定价和容量控制策略是收益管理两种常用的控制手段.作为收益管理的一个重要分支,容量控制策略对于解决企业资源分配等问题发挥着重要的作用,也是航空、铁路等客运行业的相关学者在进行运输资源优化配置策略研究时所采取的主要方法.
早期的单区段席位控制问题以差别定价为背景,探讨不同票价等级的票额限制策略,具有代表性的是期望边际收益(EMSR)模型,主要包括EMSR-a以及之后在此基础上进行改进的EMSR-b模型[1-2].从20世纪80年代开始,收益管理转向以研究网络条件下的OD控制问题为重点[3-6],控制策略主要包括分段的或非嵌套的预订限制策略、虚拟嵌套控制及投标价格控制[7],这些研究通常以需求独立性假设为前提,忽略不同客运产品或不同价格等级之间的相互影响.为克服需求独立性的假设,将旅客选择行为理论嵌入OD控制策略成为目前收益管理研究的热点,如Van等[8]基于旅客选择行为研究了虚拟嵌套座位控制收益管理问题,钱丙益等[9]基于旅客的buy-up行为,利用嵌套型席位控制策略建立了两个票价等级的席位控制模型,并利用粒子群算法进行求解.
以上研究主要针对单一客运产品的建模,未考虑不同客运产品之间的相互影响及能力的综合利用.本文针对当前我国铁路客运单一票价的现实特点,基于旅客在不同客运产品供需不匹配下的转移行为,探讨铁路企业不同客运产品多区间客票联合优化的网络型收益管理问题.以高速列车的一等座和二等座为例,将两种不同类型席位看作铁路客运中两种不同的客运产品,在旅客向上购买(buy-up)和向下购买(buy-down)概率已知的条件下,以各OD区间两种席位的预订限制票额为决策变量,以整体收益最大为目标,建立了一个带约束的非线性整数规划模型,利用线性规划与粒子群算法相结合的方法对模型进行求解,并通过算例分析旅客不同的选择行为对最优决策及整体收益的影响.
1 模型构建
1.1 问题描述
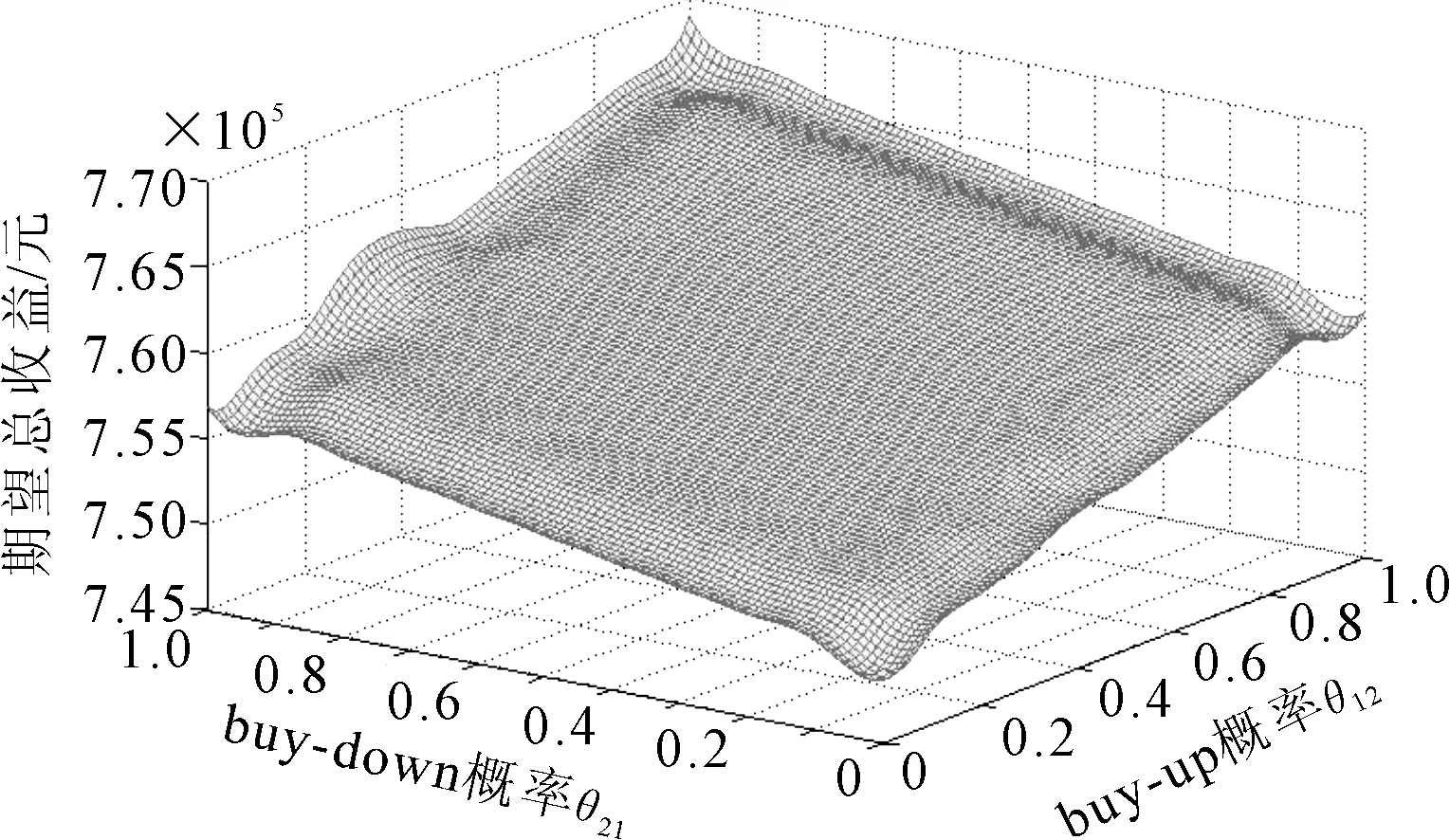
假定在一条客运专线上共有K个停靠站(始发站编号为1,其余各停靠站依次编号),每个停靠站都可以上下乘客,从始发站开始相邻两个停靠站之间的区段依次标记为区段1,区段2,…,区段K-1;用(i,j)表示从停靠站i到j的OD区间(1≤i (1≤m≤K-1,k=1,2) (1) 本文研究的目的就是在风险中立原则下,将旅客双向转移行为嵌入列车席位控制模型中,通过确定一等座和二等座的联合预订决策,以实现两种不同客运产品的期望总收益最优. 1.2 模型构建 对于任意区间(i,j),假定两种席位的初始需求d1ij和d2ij确定,则对于不同的预订限制C1ij和C2ij来说,单区间内列车的收益可能会出现以下四种情形: 情形1C1ij>d1ij且C2ij>d2ij由于两种席位均供大于需,因此,(i,j)区间内对两种席位需求的旅客而言,不存在相互转移的行为,列车总收益为 Rij=P1ij×d1ij+P2ij×d2ij (2) 情形2C1ij≤d1ij且C2ij≤d2ij由于两种席位均供不应求,同样,(i,j)区间内对两种席位需求的旅客而言,不存在相互转移的行为,列车总收益为 Rij=P1ij×C1ij+P2ij×C2ij (3) 情形3C1ij>d1ij且C2ij≤d2ij(i,j)区间内,二等座的“溢出”客流将以θ12的比例转向一等座,一等座的需求转变为d1ij+θ12(d2ij-C2ij),列车总收益为 Rij=P1ij×min (C1ij,d1ij+θ12(d2ij-C2ij))+ P2ij×C2ij (4) 情形4C1ij≤d1ij且C2ij>d2ij类似情形3,列车总收益为 Rij=P1ij×C1ij+P2ij× min (C2ij,d2ij+θ21(d1ij-C1ij)) (5) 在同时对两种席位采取席位控制策略时,从以上可能出现的四种结果可知,对于给定的预售上限C1ij和C2ij来说,只有当某种席位出现供需不匹配时旅客才会在两种席位间发生转移行为.为便于收益模型的建立,引入xkij(k=1,2),并规定当dkij>Ckij时,xkij=1,否则xkij=0,则以上四种情形为 Rij=P1ij×min(C1ij,d1ij+x2ijθ12(d2ij-C2ij))+ P2ij×min(C2ij,d2ij+x1ijθ21(d1ij-C1ij)) (6) 设D1ij=d1ij+x2ijθ12(d2ij-C2ij)、D2ij=d2ij+x1ijθ21(d1ij-C1ij)分别表示旅客发生转移行为之后区间(i,j)对一等座和二等座的实际需求.由于预订限制策略通常制定于预售期之前,初始需求预测具有一定的不确定性和随机性,为此本文假设旅客的购票过程为泊松过程,并设区间(i,j)对不同席位的需求强度为λkij,则k等座需求等于nk的概率为 P(dkij=nk)=(λkij)nke-λkij/nk!(k=1,2)(7) 进而可得一等座期望销售量: E[min(C1ij,D1ij)]= Pr(d1ij)Pr(d2ij) (8) 二等座期望销售量: E[min(C2ij,D2ij)]= Pr(d1ij)Pr(d2ij) (9) 引入充分大常数M对x1ij和x2ij的取值进行约束,约束表达式为 dkij-Ckij≤Mxkij且(xkij-1)×M (10) 可得在随机离散需求下,考虑双向替代影响,高速列车两种不同席位在区间(i,j)内的期望总收益为 由此,列车期望总收益最大化问题转化为 s.t. (12) 与网络收益管理静态席位控制模型中的概率非线性规划模型(PNLP)相比,上述模型在其基础上进行了改进,将旅客双向转移行为有效嵌入两种不同席位客票收益的联合优化中,而不再将两者的需求看作是互相独立的. 以上模型属于非线性整数规划模型,随着停靠站数量的增加,OD数量及模型的规模呈现阶乘级增长,传统的求解方法很难快速高效求解问题.文献[11]在求解两个票价等级的铁路客票分配问题时提出了一种将线性规划与粒子群算法相结合的启发式算法,并从求解时间和结果等方面将该算法与LINGO等求解方法进行了的比较,表现出了更好的效果.如果不考虑旅客的选择行为,并将两种不同席位类型看作单一席位的两个不同价格等级,考虑两个价格等级客票共用同一种席位资源的情形,本文所建模型将退化为类似文献[11]所求解的模型. 首先设计预订限制的变量和PSO系统中的粒子之间的映射规则:由于席位类型的数量是2,并且行程的个数是K(K-1)/2,变量的总数是K(K-1),因此为铁路票额分配问题设置了一个n=K(K-1)维的搜索空间,即设定单个粒子为n维向量. 0≤S1ij≤λ1ij+θ12max (0,λ2ij-S2ij) (13) 对于二等座销售量S2ij同样满足上述条件.为此,类似xkij,引入ykij,并规定: λkij-Skij≤Mykij且(ykij-1)M<λkij-Skij (14) 可得以下线性规划Q: s.t. (15) (16) 式中:rh为一个n维向量,各元素取值在(-r,r)区间内服从均匀分布,且r为正整数,可根据实际情况而定. (17) 4) 粒子位置更新 粒子通过具有定向速度向量的搜索空间飞行以找到更好的解,其中速度矢量包含随机分量,并根据历史信息和粒子间的信息进行更新,粒子位置及速度按照下述方式进行更新: (18) (19) 假设列车按16节编组,每个区段一等座和二等座的最大供给数量分别为448和672,考虑一个由五个停站点、四个区段组成的铁路客运专线,该条客运专线共服务于10个不同的OD区间.各OD区间一等座和二等座票价满足:P1ij=1.5P2ij,满足运价率随运距的增加而减小的原则,其中,P2ij及区间(i,j)内对一等座和二等座的需求强度λ1ij和λ2ij的取值见表1. 图1 模型求解算法流程图 ij23451(185,150,200)(310,135,150)(444,118,136)(553,91,132)2(130,84,128)(279,92,134)(399,110,180)3(150,115,225)(279,116,232)4(135,78,186) 表2 θ12=θ21=0时和Ckij的值 表3 θ12=0、θ21=0.3时和Ckij的值 表4 θ12=0.3,θ21=0时和Ckij的值 图2 期望总收益R随双向转移概率变化趋势 由表2~3可知,当旅客只存在buy-down单向转移行为时,一等座在各区间的最优控制票额基本保持不变,旅客的buy-down行为主要影响二等座的最优控制决策;相反,表2和表4的对比表明,若旅客只存在buy-up单向转移行为时,二等座最优席位控制决策基本不变,旅客的buy-up行为主要影响一等座的最优控制决策.由图2可知,随着旅客任一类型转移概率的增加,企业整体收益也将增加,这与实际是相符的,铁路客运通常服务于多个OD区间,在单一票价模式下,不同区间的票额分配在直接决定客运产品收益的同时,导致旅客选择行为发生了转变,即促使旅客对不同客运产品的实际需求发生了变化,将旅客选择行为嵌入票额分配决策中进而加以主动引导和利用,能够促使不同客运产品的需求结构向着可进一步提高企业整体收益的趋势重新得以调整.而随着席位控制对旅客选择行为影响程度的增加,最优决策将发生不同程度的改变,企业整体收益也随之增加. 在席位票价及初始需求分布已知条件下,将旅客双向转移行为嵌入两种不同铁路客运产品的客票预订限制策略中,针对单条线路、多个区段的列车网络型收益管理问题,建立一个带约束的非线性整数规划模型,并通过将线性规划与粒子群算法相结合的方法对模型进行求解,获得了实现期望总收益最大化的一个控制策略.最后,通过算例分析旅客不同选择行为对最优决策和期望总收益的影响. 实际中,票额预订限制策略制定于预售期前,所建模型是静态的,而由于需求预测具有一定的误差,在预售期内必须根据实际需求的变化,反复对模型进行优化,以实现对客票预售限额的动态调整.同时,为追求整体收益的最大化,在未来收益管理的研究中,旅客的选择行为需要进行更深层次的分析,另外,如何将旅客选择行为有效融入更多种(三种或三种以上)铁路客运产品的客票收益管理问题中也是进一步研究的重点. [1]LITTLEWOOD K. Forecasting and control of passenger bookings[C]. AGIFORS 12th Annual Symposium Proceedings,1972. [2]BELOBABA P P. Air travel demand and airline seat inventory management[D]. Cambridge: MIT,1987. [3]TALLURI K T, VAN R G J. An analysis of bid-price controls for network revenue management[J]. Management Science,1998,44(11):1577-1593. [4]MCGILL J, VAN R G J. Revenue management: research overview and prospects[J]. Transportation Science,1999,33:233-256. [5]BELOBABA P P, HOPPERSTAD C. Boeing/MIT simulation study: PODS results update[C]. AGIFORS Reservations and Yield Management Study Group Symposium Proceedings,1999. [6]CARRIER E. Modeling airline passenger choice: passenger preference for schedule in the passenger origin-destination simulator (PODS)[D]. Cambridge: MIT,2013. [7]TALLURI K T, VAN RYZIN G J. The theory and practice of revenue management[M]. New York :Springer,2005. [8]VAN R G, VULCANO G. Computing virtual nesting controls for network revenue management under customer choice behavior[J]. Manufacturing & Service Operations Management,2008,10(3):448-467. [9]钱丙益,帅斌,陈崇双,等.基于旅客buy-up行为的铁路客运专线收益管理模型[J].铁道学报,2013,35(8):10-15. [10]王莹,郝丹,李海鹰,等.基于供需匹配的铁路运输通道客流分担率研究[J].铁道学报,2014,36(12):1-5. [11]YOU P S. An efficient computational approach for railway booking problems[J]. European Journal of Operational Research,2008(2):811-824. Joint Optimization of Train Seat Inventory Based on Bidirectional Diversion of Multiple-class Demands LI Gaoling PENG Qiyuan (SchoolofTrafficandTransportation,SouthwestJiaotongUniversity,Chengdu610031,China) Taking into account the substitution effect of different seats, this paper integrates the two-way transfer of passengers into the passenger-ticket optimization problem of a single line, multi-section and two different passenger transport products. Taking the booking limits of the two classes of seats of each itinerary as the decision variables and the total revenues as the objective, a nonlinear integer programming model with constraints is established for the first-class and second-class seats under a known condition of the probabilities of passengers’ buy-up and buy-down behavior. In addition, a method of combining linear programming with particle swarm optimization is used to solve the model. The results show that the different choice behavior of passengers has different effects on the optimal decision and the overall income. For any kind of transfer behavior, the total income is expected to increase with the increase of the transfer probability. substitution effect; joint optimization; booking limits; expected total income 2017-05-31 U293.13 10.3963/j.issn.2095-3844.2017.04.033 李杲岭(1989—):男,硕士生,主要研究领域为交通运输规划与管理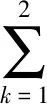
2 模型求解
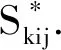


3 模型数值验证与分析






4 结 束 语
