基于隐马尔科夫模型的滚动轴承性能退化评估

周建民，郭慧娟，张 龙

（华东交通大学机电与车辆工程学院，江西 南昌330013）

基于隐马尔科夫模型的滚动轴承性能退化评估

周建民，郭慧娟，张 龙

（华东交通大学机电与车辆工程学院，江西 南昌330013）

滚动轴承的运行状态与退化程度息息相关，若能对轴承的退化程度进行在线定量评估，则可使设备维护策略的制定具有针对性。本文对无故障样本进行小波包分解得到能量值并将其和时域值作为原始特征。对原始特征进行降维后分为训练和待测数据，用无故障样本训练HMM模型，稳定后保持模型不变通过迭代的方式将待测样本输入到训练好的HMM，获得最大输出似然概率作为性能退化程度指标，用轴承加速疲劳试验和包络解调对本文的结论进行验证。本文提出的性能退化方法得到的结论与轴承加速疲劳试验得到的结果一致。

隐马尔科夫；滚动轴承；小波包分解；时域特征；性能退化评估；包络解调

轴承是旋转机械的重要组成部分，旋转机械的失效多数是由轴承故障引起的，轴承的状态监测和故障诊断成为近年来的研究热点[1]。传统的轴承故障诊断模式侧重先发现故障再进行维修，而性能退化评估是一种主动的维修方式，通过分析机械设备的振动数据，对机械设备进行相应的性能评估，了解设备所处的状态进而避免不必要的经济损失，这就是性能退化评估的实质。

性能退化评估方法有两种：一种是直接用时域指标或是非线性统计参数作为性能退化指标，如均方根值、分形维数等，Liao H等通过特征提取方法得到均方根值和峭度，将它们作为评价指标进行非线性拟合，进行轴承的可靠性评估；另一类是提取特征向量，比较待测样本与无故障样本之间的几何距离（如基于支持向量描述SVDD的方法）或统计相似度（如高斯混合模型GMM和隐马尔科夫模型HMM）[2]。陈斌等对不同故障程度的轴承数据分别建立SVDD模型，再利用待测样本到各超球体中心的相对距离来建立轴承故障程度的预测模型[3]。李巍华等将小波包熵与GMM相结合，通过计算每一运行状态对应的GMM相对基准GMM模型的偏离程度来判断轴承的实际退化程度[4]。Yu等利用GMM识别轴承早期阶段的轻微退化，并揭示了轴承性能的退化传播过程[5]。Liu等考虑到多通道传感器信息包含更丰富的特征信息，采用耦合隐马尔科夫模型来评估轴承的退化状态[6]。但这些都没有实现滚动轴承的在线实时监测评估，同时单一的时域值不具有足够的一致性或敏感性，SVDD其单、多类别分类算法，都存在着正负类别样本数据信息偏离性现象，在设定C值上同样具有或多或少的不平衡性问题。GMM容易在轴承没有失效时达到取值上限，无法准确地确定轴承的失效状态。HMM用最大输出似然概率作为性能退化程度指标可以解决正负样本偏离现象和容易达到上限值的问题，而且HMM适用于大样本数据，可以实现在线实时监测评估轴承的性能退化，所以本文用HMM进行评估。

要对轴承性能评估首先要提取特征。Hong等在对轴承振动信号进行EMD分解后求取各个IMF分量的能量熵，以此作为反映实际健康状态的特征[7]。但EMD本身存在模态混淆问题，即相近尺度的信号会被分解到不同的IMF分量中[8]。康守强等为了全面地刻画滚动轴承的不同退化程度，先求出原始振动信号以及经过小波包分解后节点信号的时域、频域指标和奇异值[9]。当所提取数据的特征维数比较大时，为避免信息冗余，需对提取到的特征进行特征降维，常用的降维方法有主成分分析和局部线性嵌入等。张蕾将PCA（principal component analysis）与局部逼近神经网络相结合，从而在对多维特征向量进行维数压缩的基础上，利用神经网络进行设备的性能退化评估[10]；LLE（locally linear embedding）是一种试图保留数据点局部性质的非线性流行降维方法[11]。其本质思想就是利用局部的线性特征向整体线性特征进行逼近，全局结构的信息由相互重叠的局部信息提供，与PCA相比LLE可以保留整体的几何性质。轴承的振动是非平稳的，故本文用小波包变换进行滚动轴承的特征提取，用LLE对提取到的高维数据进行降维。把总特征值矢量化后分为训练数据和待测数据，用训练数据训练HMM，稳定后输入待测数据，得到该模型的似然输出概率，并且比较降维前后退化曲线的变化。最后用希尔伯特变换验证实验结果的可靠性，用轴承加速疲劳寿命实验验证此方法的可行性。

1 特征提取及降维

1.1 小波包变换

小波包变换的实质是对未分解的高、低频信号再次分解，是一种自动选择频带范围及自动完成频带匹配的时频分析技术[12]。滚动轴承的振动信号与所选的小波基函数越相似，分解的效果就越好，假设小波包函数，其中 n 为平移参数，l为调节参数，m 为尺度函数，当 l=1，m=n=0 时，此函数即为小波基函数，当l≠1时有

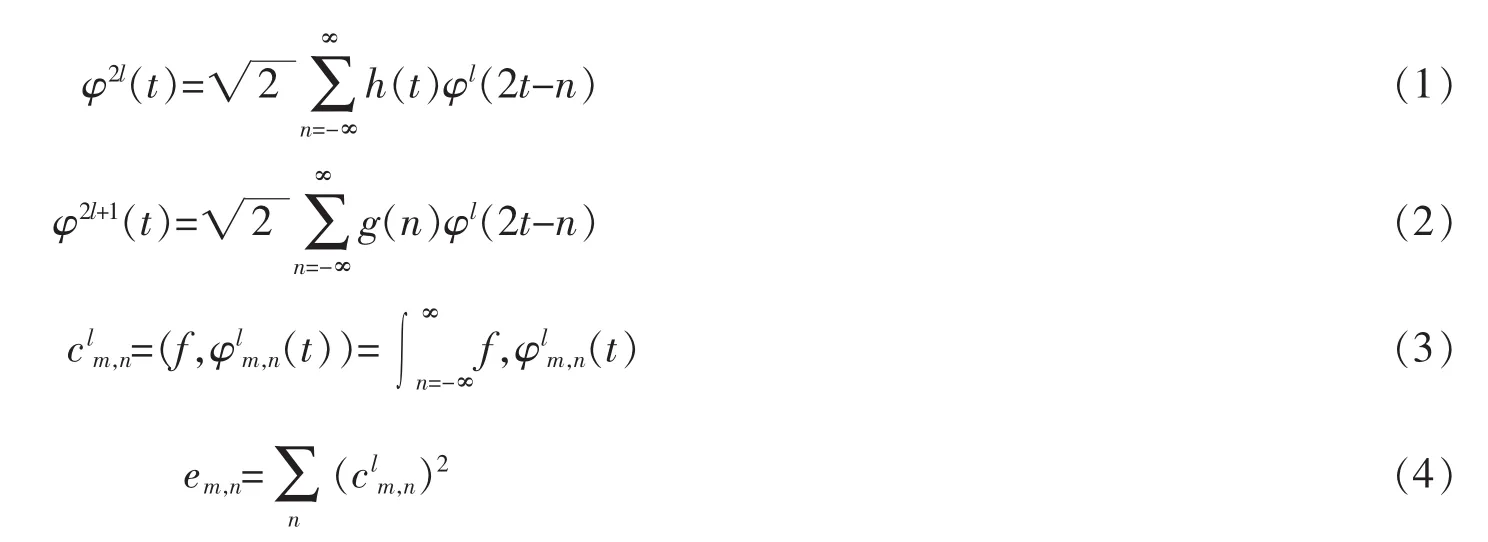
式（1）～式（4）分别为尺度方程，小波方程，能量系数方程，节点能量方程。

1.2 LLE特征降维

由于本文中数据样本较大，提取到的高维特征之间难免有冗余现象，所以要对提取到的特征进行降维约简。LLE[13]是一种试图保留数据点局部性质的非线性流行降维方法，利用局部的线性特征向整体线性特征进行逼近，假设每个数据点与它的邻近点位于流形的一个线性或近似线性区域中，将全局非线性转化为局部线性是 LLE的基本思想，全局结构的信息由相互重叠的局部信息提供[14]。 设 X＝［x1，x2，…，xn］，xi∈RD为初始高维观测向量，Y＝［y1，y2，…，yn］为所求的低维向量。首先对每一个初始的高维样本点在其高维空间中寻找k个近邻点进行局部重建，并计算重建后的权值，使满足样本点的重建误差最小。

xij（j=1，2，…，k）为 xi的 k（k＜N）个近邻点，距离公式是xi与xij之间的权值。要保证重建之后的误差值最小必须满足样本与其邻近点之间的拓扑结构不变[15]，则有，Yi需满足，I是N维单位矩阵。所以，优化问题即为下列的约束优化问题

其中，M=（I－W）T（I－W）。 用 Lagrange 乘子式法来求出 MYT＝λYT，计算得所求的嵌入坐标就是 M 的特征向量。取M的d个最小非零值的特征相应的特征向量作为维数较低的坐标Y。一般情况下特征值的最小值几乎是0，所以，输出结果就可以取2～（d＋1）间的特征值对应的向量。

1.3 特征标量化

对离散的隐马尔可夫模型进行建模的时候，观测值必须是有限个数的离散值，本文需对特征值进行标量化[16]。根据信号的幅值把信号分N－1个区域，把相邻的N个区域映射为N个离散的数值，训练用码本就是由振动信号生成每个区域的索引为index（x），其定义为

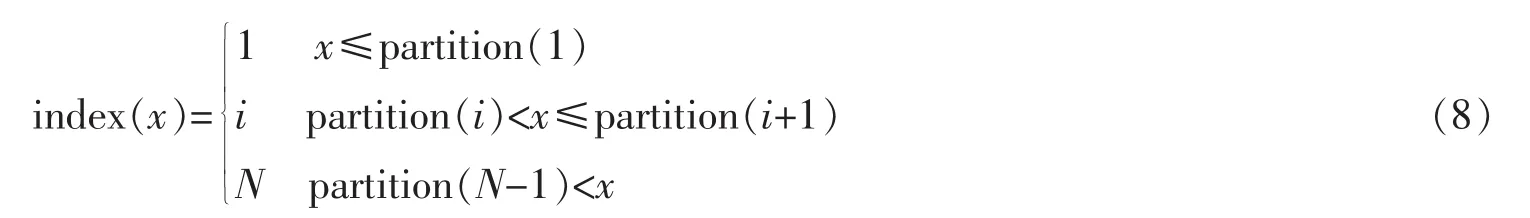
i为自然数，定义一个长为N的码本向量长度与一个N－1的分区向量partition是完成标量化必需的，由N－1个按照升序排列的分区值分区向量将振动数据分为N个区域，按照该码本向量分区的端点值或该区域的平均值为每个区域赋值。信号幅值谱x要进行标量化处理。

1.4 整体框架流程图

基于HMM的性能退化评估模型技术路线如图1所示。具体步骤如下：

1）利用小波包与时域特征提取方法对轴承无故障信号进行特征提取，所得的特征样本作为训练数据。

2）用训练数据训练初始化后的HMM模型，待模型稳定后把待测数据特征提取后保持模型不变通过迭代的方式输入到训练好的模型中，停止迭代后描绘出滚动轴承的性能退化曲线。

3）对待测数据进行LLE特征降维之后重新输入到HMM模型中，比较降维前后的性能退化曲线。

图1 技术路线流程图Fig.1 Technical route flow chart

2 实验结果分析

2.1 试验台介绍

图2是完成轴承的加速疲劳寿命的试验台[17]。通过杠杆对轴和轴承施加一个约26.66 kN的径向载荷。转速保持在2 000 r/min，采样频率为20 kHz，用油循环系统来调节润滑油的流量与温度参数。磁性螺塞安装在反馈油的管道之内。试验中用到的轴承型号为Rexnord ZA-2115，它是双列滚柱轴承，PCB353B33是灵敏度比较高的压电加速度传感器，试验中8个传感器分别被安装在各轴承垂直与水平方向上。数据采集的间隔是10 min，其长度是20 480个点。本文取每个样本的前8 192个数据点进行分析。振动信号在每个给定的时间段记下持续1 s的快照然后保存数据到文件中。本文采用轴承1的退化数据，对轴承1进行性能退化评估。

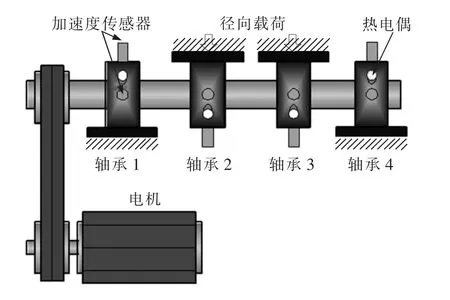
图2 轴承失效试验台示意图Fig.2 Diagram of bearing failure test stand

2.2 时频域特征参数分析

小波包分解后的结点能量值和时域特征，如均值、均方根值、峰峰值、方根幅值、绝对平均值、方差等有量纲参数以及歪度、峭度等无量纲参数可用来反映轴承的退化状态[18]，本实验对轴承1每个样本都提取了8 192个点进行分析，统计结果图3示。

从图3可以看出均方根值和峰峰值在约第700个样本时才有明显上升趋势，不利于轴承早期故障的发现，峭度虽在第530个样本时有较明显变化，但在约第700个样本时先减后增，与轴承的退化性能不一致，不利于故障的跟踪发现，仅用某一个时域特征值不能准确地反映滚动轴承的性能退化趋势。本文将3个时域特征值和小波包分解方法提取到的8个能量特征值作为总特征值输入隐马尔科夫模型中。

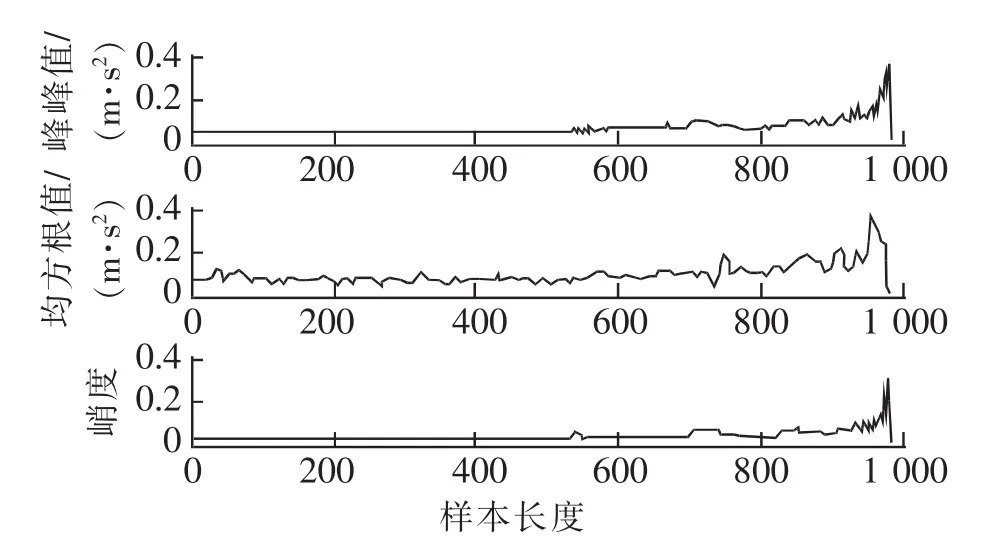
图3 全寿命周期内时域特征Fig.3 Time domain characteristics of the whole life cycle

2.3 基于HMM的性能退化评估

隐马尔科夫模型[19]可记为λ=（N，M，π，A，B）。其中N为马尔科夫链的状态数，有正常、初期故障、恶化、深度恶化以及失效5个状态；M为每个状态下所有可能出现的观测值，本文M为11；π为初始概率分布矢量；A为模型的状态转移概率矩阵，参数A与π通常均匀选取或随机选取；B为模型的观测值概率矩阵。

模型初始化完成之后，将前200组数据输入到模型中进行训练，同时在程序中设置当其两次输出值之间的差值小于10-3时停止迭代，模型训练完毕。然后保持模型不变通过迭代的方式将待测数据输入到已经训练好的模型当中，当程序停止迭代时，得到一系列滚动轴承的似然概率输出值，但是，由于在迭代的过程中很快接近零值，所以程序中尽量把比例系数提高，其输出的相似概率也比较小，本文用对数似然概率来表示。在得到其对数似然概率值之后，用plot函数画出滚动轴承的性能退化曲线，如图4所示。因滚动轴承所处的状态和对数似然概率值的大小有一定的关联，对数似然概率值越大代表轴承目前所处的状态越与滚动轴承的正常状态相接近，否则，对数似然概率值越小轴承所处的状态越偏离滚动轴承的正常状态。从图4中可以看出在第533个样本处出现了早期故障，在第699个样本处故障恶化，在第902个样本处出现深度恶化，由于冲击过大使其原有的特征不明显，故曲线有较大的上下波动，在第952个样本后曲线急剧下降，这时轴承完全失效。但是退化曲线在第699个样本和第902个样本之间有先减小后增大的趋势，与其退化趋势不一致，所以对时频域特征进行降维。经过LLE特征降维之后，样本特征从11维降到5维，滚动轴承1的对数似然概率值在整个轴承寿命周期内的变化趋势和概率值随着程序中迭代步数的变化如图5所示。

从图5中可以看出，特征降维后早期故障仍然发生在第533个样本处，第698个样本和第902个样本之间是故障恶化阶段，相比降维之前其曲线与滚动轴承的退化趋势保持一致，每一个故障阶段比降维前更容易区分，与降维前一样，在第952个样本处滚动轴承1的对数似然概率值一直呈下降趋势，此时滚动轴承已经完全失效。

图4 轴承1的性能退化曲线Fig.4 Performance degradation curve of Bearing 1

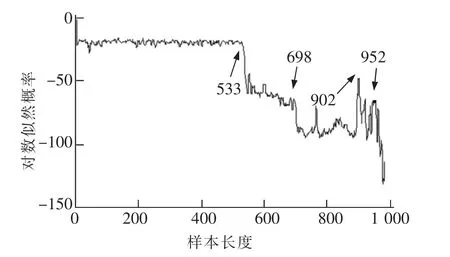
图5 降维后轴承1的性能退化曲线Fig.5 Performance degradation curve of Bearing 1 after dimension reduction

3 包络谱分析

为了验证初始故障发生在第533个样本评估结果的正确性，采用基于经验模态分解（EMD）和Hilbert包络解调的包络谱分析方法分析第533个样本和第532个样本的频谱。用EMD把它们分解成若干个简单的固有模态函数（IMFs），然后用希尔伯特包络解调对IMF1进行分析，因为IMF1是振动信号中频率最高且包括振动信息最详细的振动信号[20]。解调结果如图6（b）图所示，可以看出在频率为231 Hz时有一个明显的谱峰，这与外圈球通频率（BPFO）236.4 Hz非常接近。此外，存在着明显的谐波频率特性。图6（a）是第532次采样的包络线的频谱图，图中没有明显的谱峰（在第532个样本之前的样本显示相同的结果）。因此，可以推断在第533个样本处发生外圈初始故障，分析结果与之前的评估结果一致。

图6 无故障和初始故障样本的包络谱分析Fig.6 Envelope demodulation of normal and early fawlt sample

4 结论

首先提取无故障样本的时域特征和小波包分解特征作为轴承1总的特征统计参数，先用无故障特征训练HMM模型，再保持模型不变通过迭代的方式将待测样本数据输入到模型中进行预测评估，不需要轴承的历史失效数据，实现了滚动轴承性能退化的在线实时监测评估，实验表明，时域特征和小波包分解后特征加一起比单独的时域特征更能表征全寿命周期内轴承的性能退化趋势，更有利于早期故障的发现，对滚动轴承退化性能进行评估的时候，降维之后使得特征更明显，复杂度和迭代次数也明显减少，最后用经验模态分解和希尔伯特包络解调方法验证了本文所提方法结论的正确性。

[1]艾树峰.基于双树复小波变换的轴承故障诊断研究[J].中国机械工程，2011，22（20）：2446-2451.

[2]LIAO H，ZHAO W，GUO H.Predicting remaining useful life of an individual unit using proportionalhazards model and logistic regression model[C]//Reliability and Maintainability Symposium，2006，IEEE，2006：127-132.

[3]陈斌，阎兆立,程晓斌.基于SVDD和相对距离的设备故障程度预测[J].仪器仪表学报，2011，32（7）：1558-1563.

[4]李巍华，戴炳雄，张绍辉.基于小波包熵和高斯混合模型的轴承性能退化评估[J].振动与冲击，2013，32（21）：35-40.

[5]YU J B.Bearing performance degradation assessment using locality preserving projections and gaussian mixture models[J].Mechanical Systems and Signal Processing，2011（25）：2573-2588.

[6]LIU T，CHEN J，DONG G M.Zero crossing and coupled hidden Markov model for a rolling bearingperformance degradation assessment[J].Journal of Vibration and Control，2014，20（16）：2487-2500.

[7]HONG S，ZHOU Z，ZIO E，et al.An adaptive method for health trend prediction of rotating bearings[J].Digital Signal Processing，2014（35）：117-123.

[8]郑近德，程军圣，杨宇.改进的 EEMD 算法及其应用研究[J].振动与冲击，2013，32（21）：21-26，46.

[9]康守强，李祝强，杨广学，等.小波包-局部线性嵌入算法在滚动轴承故障程度识别中的应用[J].仪器仪表学报，2014，35（3）：614-619.

[10]张蕾，黄其新，JAY LEE，等.基于 PCA-CMAC 的设备性能园化评估[J].东南大学学报：英文版，2005，21（3）：299-303.

[11]ROWEIS S T，SAUL L K.Nonlinear dimensionality reduction by locally linear embedding[J].Science，2000，290（5500）：2323-2326.

[12]于波，徐雪娇，郑听.基于小波包分解的能量特征提取在旋转机械故障诊断中的应用研究[J].化工自动化及仪表，2016，43（10）：1056－1059.

[13]黄移军.基于局部线性嵌入的高维数据降维研究[D].长沙：中南大学，2009．

[14]SU Y T，LIN M H，LEE M H.The effects of surface irregularities on roller bearing vibrations[J].Journal of Sound and Vibration，1999，12（2）：225-242．

[15]冯长建.HMM动态模式识别理论、方法及在旋转机械故障诊断中的应用[D].杭州：浙江大学，2002.

[16]DONG M，HE D，BONERJEE P，et al.Equipment health diagnosis and prognosis usinghidden semi-Markov models[J]．The Internatioral Journal of Advanced Manufactaring Technology，2006，30（7）：738-749．

[17]周建民，徐清瑶，张龙，等.基于小波包Tsallis熵和FCM的滚动轴承性能退化评估[J]．机械传动，2006（6）：110－115．

[18]张龙，黄文艺，熊国良，等.基于多域特征与高斯混合模型的滚动轴承性能退化评估[J].中国机械工程，2014，25（22）：3066-3072.

[19]朱义.基于 CHMM的设备性能退化评估方法研究[D].上海：上海交通大学，2009.

[20]MA J，WU J，FAN Y，et al.The rolling bearing fault feature extraction based on the LMD and envelope demodulation[J].Mathematical Problems in Engineering，2015（6）：1-13.

Rolling Bearing Performance Degradation Assessment Based on Hidden Markov Model

Zhou Jianmin,Guo Huijuan,Zhang Long
（School of Mechatronics&Vehicle Engineering,East China Jiaotong University,Nanchang 330013,China）

The running condition of rolling bearing is closely related to the degree of its degradation.If the degradation degree of rolling bearings can be assessed online quantitatively,the equipment maintenance strategy will be pertinent.This paper makes the node energy values decomposed of non-faulty samples by wavelet packet,which are taken together with time-domain features as the original characteristics of the signals.The original features are classified into training data and test data after the nonlinear flow-based dimensionality reduction.The HMM model is trained by the non-faulty samples.After the model is stabilized and the model is maintained unchanged,samples to be tested are input into the trained HMM through iterations.Then,the maximum output likelihood is obtained as performance degradation index,which is adopted to evaluate the performance of rolling bearings.The proposed method is verified by fatigue life test of the bearing and the envelope demodulation.Results of performance degradation method are in agreement with those obtained from the accelerated fatigue tests of bearings.

Hidden Markov；rolling bearing；wavelet packet decomposition；time domain feature；performance degradation assessment；envelope demodulation

TN91，TH17

A

（责任编辑 刘棉玲）

1005-0523（2017）04-0110-07

2017－03－23

国家自然科学基金项目（51205130，51665013）

周建民（1975—），男，教授，博士，研究方向为智能诊断、无损检测等。