GPS/GLONASS/BDS多模融合伪距单点定位模型精度分析

王涛

(安徽理工大学 测绘学院,安徽 淮南 232001)

GPS/GLONASS/BDS多模融合伪距单点定位模型精度分析

王涛

(安徽理工大学 测绘学院,安徽 淮南 232001)

GNSS伪距单点定位速度快且不存在整周模糊度问题,其原理简单易于编程实现,所以在进行GNSS数据处理时,经常用到该方法。本文以GPS、GLONASS、BDS多模融合为例,简单介绍多模融合存在的坐标统一、时间基准统一问题,再详细介绍多模融合伪距单点定位原理以及解算模型,基于Visual Studio2010平台,编写GPS、GLONASS、BDS多模融合的伪距单点定位及单点测速程序。结合相关算例,对该程序多系统伪距单点定位的精度以及单点测速精度进行分析。

GPS/GLONASS/BDS;伪距单点定位;单点测速;精度

0 引 言

随着中国卫星导航的发展,多模融合定位成为未来GNSS的重要发展方向,多模融合可以很好地增加测站接收卫星数目,形成更好的空间几何布局,从而降低精度稀释因子(DOP),提高导航定位的稳定性和可靠性[2]。伪距单点定位速度快且不存在整周模糊度问题,而且其原理简单易于编程实现,所以在进行GNSS数据处理时,经常用到该方法[3]。此前众多学者对GPS/BDS、GPS/GLONASS和GPS/BDS/GLONASS的研究已取得了丰硕的成果,张辉等[4]对GPS/BDS系统组合的可见性和定位精度进行了仿真;唐卫明等[5]利用实测数据对GPS/BDS系统组合模拟不同遮挡环境下的可见卫星数、PDOP值以及三维导航可用性进行了研究;李鹤峰等[6]利用实测数据验证了GPS/BDS/GLONASS组合导航算法的正确性;何俊等[7]根据MGEX网中的13个不同区域的监测站数据,研究了GPS、BDS、GLONASS在全球不同地区的可见性以及组合定位时的随机模型,但对于组合系统的单点测速问题,还是值得研究的。

为此,本文先介绍GPS、GLONASS、BDS多模融合的时空统一问题,再详细介绍伪距单点定位解算模型及单点测速模型,基于Visual Studio2010平台,编写GPS、GLONASS、BDS多模融合的伪距单点定位程序。结合唐家会煤矿的实测数据,对该程序多系统伪距单点定位的精度及单点测速精度进行分析。

1 GPS、GLONASS、BDS多模融合伪距单点定位解算

1.1 时空基准统一

截止2016年9月底,GPS有31颗卫星在轨运行[8],GLONASS有24颗卫星在轨运行[9],我国已成功发射了23颗北斗卫星[10]。GPS、GLONASS和BDS采用的时间基准虽互有差异,但都与世界时(UT)、国际原子时(AIT)以及世界协调时(UTC)存在着密切联系。任一瞬间GPST 与AIT 间均有一常量偏差(19 s);GLONASST与国际原子时没有固定的整秒偏差,是不连续的时间系统;BDT与协调世界时UTC(NTSC)的时间偏差小于100 ns. 但在实际应用GNSS 多模融合导航定位时,以GPST为基础,将GLONASST与BDT转化成GPST[6]:

GPST=GLONASST星历+1s×n-19,

(1)

BDT=GPST-14s,

(2)

其中,n为 UTC 与 AIT 之间的调整参数,2012年7月1日以后,该调整参数n为35,2015年7月1日以后n为36.

将CGCS2000和PZ90坐标系归化到WGS-84坐标下,文献[11]指出:CGCS2000 和WGS-84 是相容的,在坐标系的实现精度范围内,CGCS2000 和WGS-84 是一致的,可以认为CGCS2000 定位成果同属于WGS-84 坐标系成果。WGS-84与PZ90之间的转换可以采用布尔萨7参数表示[6]:

(3)

式中: ΔX=-0.47; ΔY=-0.51; ΔZ=-1.56;εx=0.076×10-6;εy=0.017×10-6;εz=1.728×10-6;m=22×10-9.

1.2 数学模型

文献[3]研究了GPS伪距单点定位,并给出了GPS伪距单点定位原理和数学解算模型。笔者对于伪距单点定位原理就不赘述了,只是在文献[3]的数学解算模型的基础上改写成GPS、GLONASS、BDS多模融合的伪距单点数学解算模型,多系统融合解算时不同系统之间视为等权,同系统间高度角定权。

单系统伪距定位待估参数有三个坐标分量和一个接收机钟差,双系统组合伪距定位待估参数有三个坐标分量和两个接收机钟差,而三系统组合伪距定位待估参数有三个坐标分量和三个接收机钟差。所以线性化伪距观测方程为

(4)

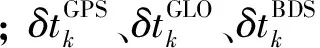
将式(4)改写成矩阵形式:

AδX=L.

(5)

当观测卫星数大于伪距定位待估参数时,可用最小二乘法求解,式(5)改写成误差方程形式:

V=AδX-L,P.

(6)

将权P定为高度角定权,所以根据最小二乘法求得改正数δX=-(ATPA)-1ATPL,

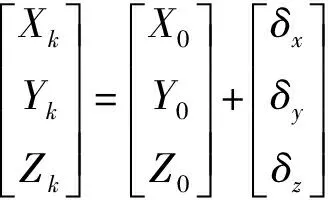
对式(4)关于时间求导,就可以得到单点测速方程[12]:

(7)

λD=l(VX-VX)+m(VY-VY)+

n(VZ-VZ)+c·dtk-c·dtj，

(8)

式中:λ为载波相位的波长;D为卫星的多普勒观测值; (VX,VY,VZ)为接收机的速度; (VX,VY,VZ)为卫星的速度;dtk和dtj分别为接收机和卫星钟差的变化率。

本文使用的是GPS的L1、L2频率、BDS的B1、B2频率、GLONASS的G1、G2频率进行伪距单点定位,电离层改正一般采用双频观测消除[3],对流层路径延迟选用简化Hopfield模型[14],考虑地球自转改正和相对论效应。对于测速,对流层和电离层延迟变化率及加速度,在采样率为1 s时可以忽略不计,但考虑相对论效应的影响。

2 程序实现及精度分析

2.1 程序实现

根据上述的GPS、GLONASS、BDS多模融合的伪距单点定位原理和相关改正模型,基于Visual Studio2010平台,编写了GPS、GLONASS、BDS多模融合的伪距单点定位程序,程序设计流程如图1所示。

2.2 算例分析

本文数据来源于2016年5月29日在内蒙古自治区鄂尔多斯市的唐家会煤矿自动化监测系统,选取了测站CTJH和CTJC站在北京时间2016年5月29日9点54分至2016年5月29日14点00分的观测数据,采样间隔1 s,两测点周围空旷,观测条件良好,截止高度角设置为10°.

1) 可见卫星数和PDOP值

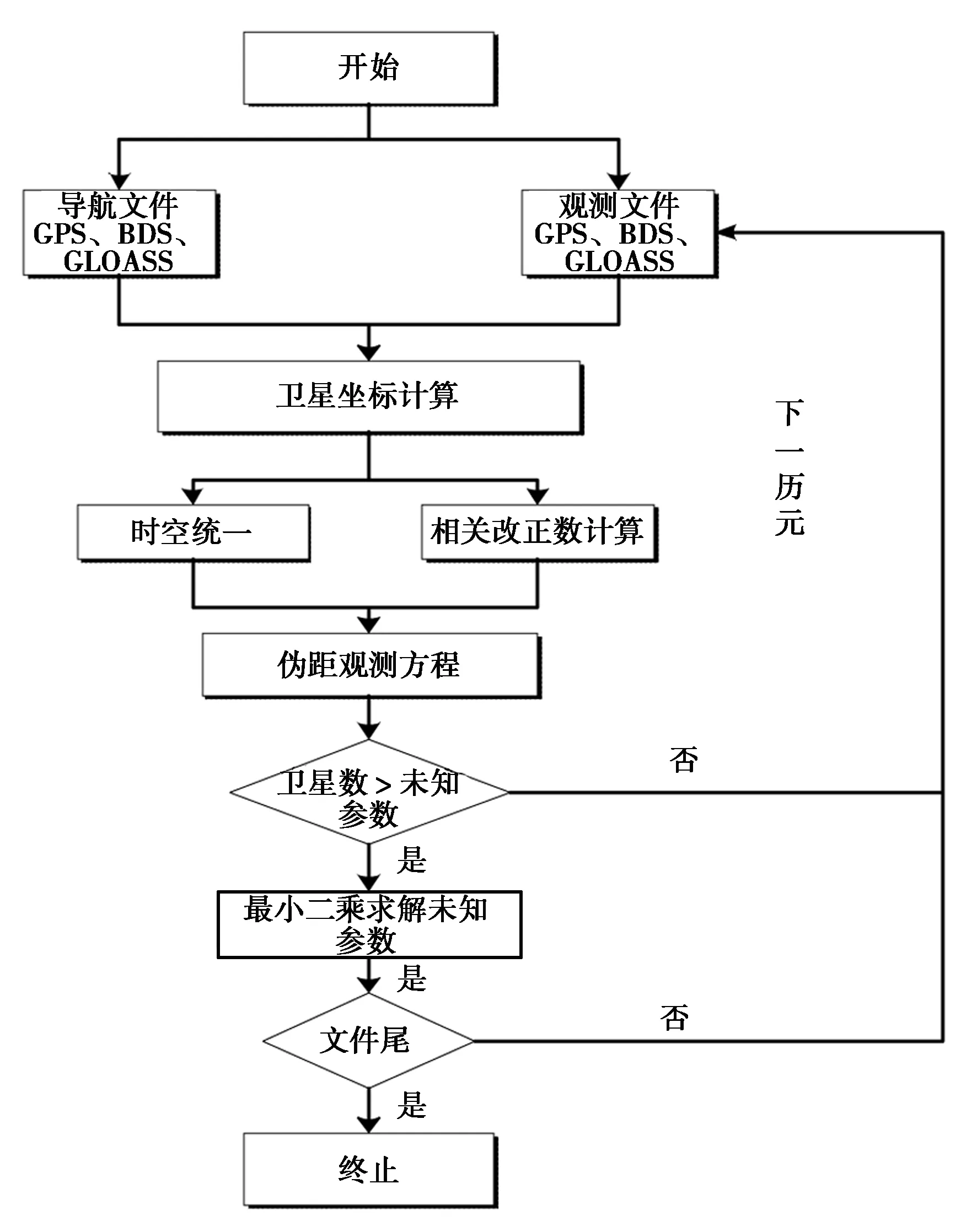
图1 GPS、GLONASS、BDS多模融合的伪距单点定位流程图

当观测卫星数较多时,卫星可以形成较好的空间几何分布,有利于降低位置精度因子,即PDOP值,有利于提高定位精度[11]。根据程序计算结果,GPS、BDS、GLOANSS及多系统融合的可见卫星数和PDOP值如图2所示(图中只给出了CTJH站的结果,CTJC站结论一致),表1示出了两站可见卫星数均值和PDOP值均值以及PDOP在(1,3)之间的分布情况。

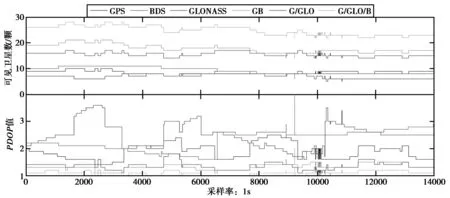
图2 可见卫星数和PDOP值

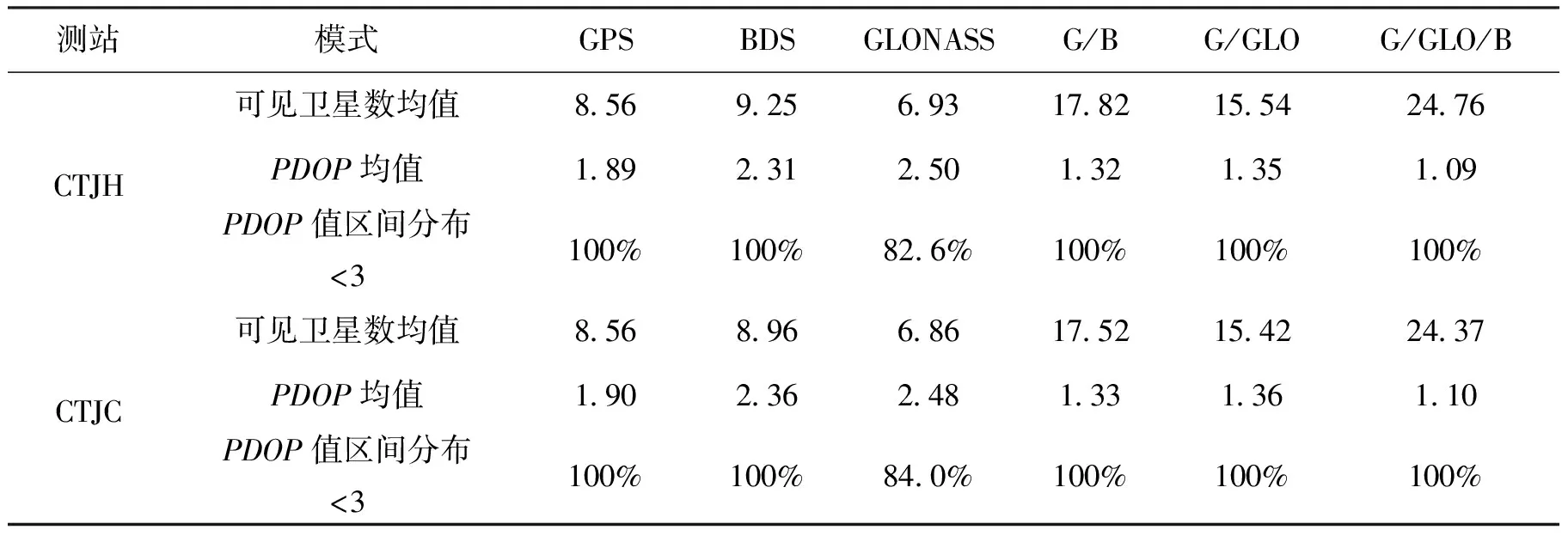
表1 两站可见卫星数均值和PDOP值均值以及PDOP在(1,3)之间的分布情况

注：G/B为GPS/BDS的缩写,G/GLO表示GPS/GLONASS缩写,G/GLO/B表示GPS/GLONASS/BDS缩写,下文同。

图2中,BDS的可见卫星数均值要大于GPS,虽然GLONASS的可见卫星数均值低于GPS和BDS系统,但满足了单系统定位时最少4颗卫星的要求,组合系统的可见卫星数均值均超过了15颗;表1中,组合系统的PDOP值比单系统低,说明组合系统比单系统拥有更好的空间几何分布,除GLONASS外,其余系统的PDOP小于3的比例均达到了100%.

2) 定位精度分析

本文所进行的精度分析,是把各历元解算坐标与测站坐标真值的差值转换为站心直角坐标系下的(N,E,U)后,着重对平面内偏差(P方向)和高程方向偏差(U方向)进行详细的分析[12]。图3示出了CTJH站GPS、BDS、GLONASS及其组合系统在平面(P方向)的定位偏差和CTJH站GPS、BDS、GLONASS及其组合系统在高程(U方向)的定位偏差。

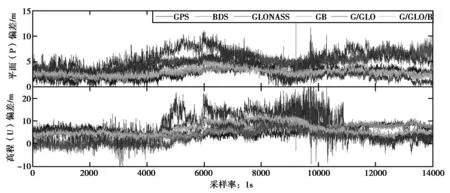
图3 GPS、BDS和GLONASS及组合系统在平面和高程方向的定位偏差

经计算,GPS、BDS、GLONASS单系统以及GPS/BDS、GPS/GLONASS、GPS/GLONASS/BDS等组合系统在测量期间内平面(P)方向内定位偏差RMS值、高程(U)方向上定位偏差RMS值如表2所示。

表2 测量期间内P、U方向内定位偏差RMS值

GPS在平面(P)方向内和高程(U)方向上的定位偏差都小于BDS、GLONASS单系统以及GPS/BDS、GPS/GLONASS、GPS/GLONASS/BDS等组合系统,这是因为BDS和GLONASS的测距精度都比GPS略差,但组合系统在平面(P)方向内和高程(U)方向上的定位结果相比BDS和GLONASS单系统都有所提高。

3) 测速精度分析

由于CTJH站和CTJC站的观测数据是静态数据,但通过静态数据模拟动态数据的方法,可以将测站的速度真值视为零。得到CTJH站GPS、BDS、GLONASS及组合系统的单点测速的结果，如图4所示(CTJC站与CTJH站结果一致)。

统计了2个测站的单点测速结果,得到各测站单点测速的均方根误差RMS如表3所示。

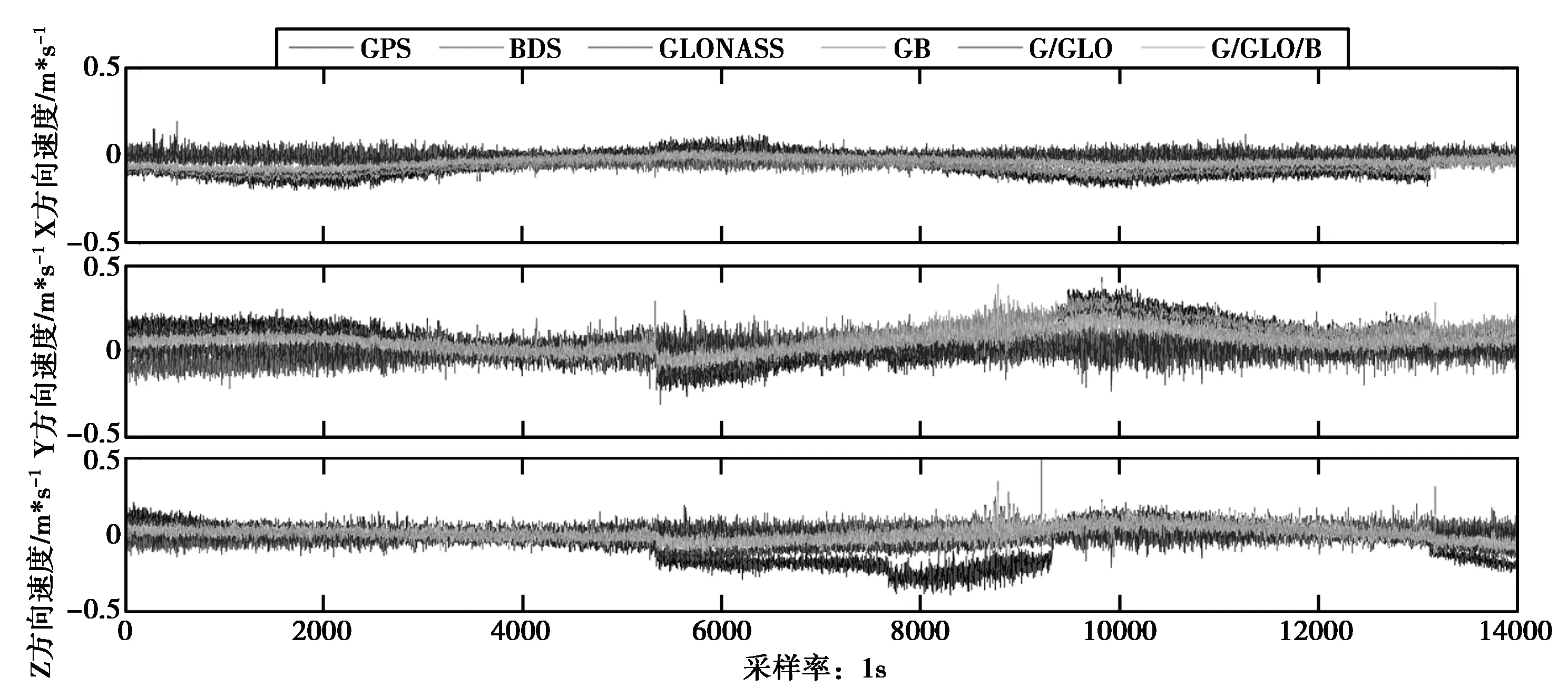
图4 GPS、BDS、GLONASS及组合系统单点测速结果

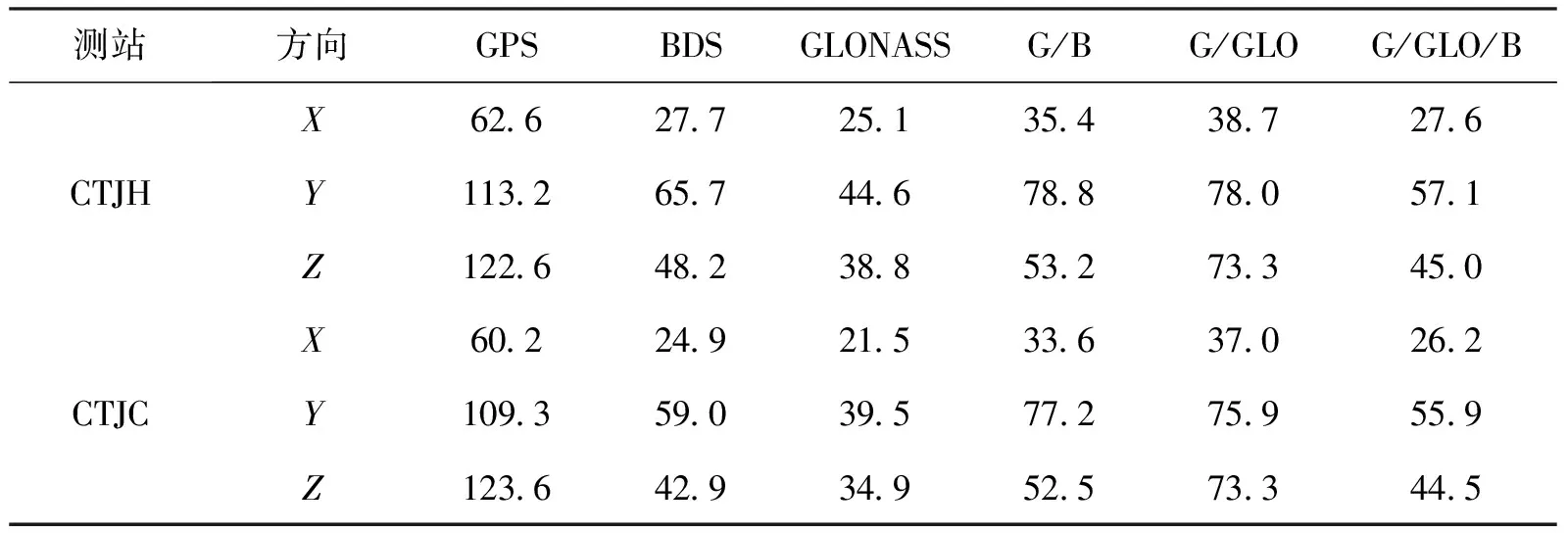
表3 测站静态测速结果统计/(mm*s-1)

从图4、表3可以看出,无论何种系统,采用原始多普勒观测值测速的均方根误差均达到dm*s-1量级,但相比GPS而言,BDS、GLONASS和组合系统的RMS值更小,达到了cm*s-1量级;X方向上的速度曲线较Y、Z方向上要平滑,X方向的测速精度高于Y、Z方向;CTJH站与CTJC站测速精度相当,这是因为两站采用相同类型的接收机,且两站之间距离较近。

3 结束语

通过上面的测试分析,可以得出:组合系统可以增加可见卫星数,降低了PDOP值,组合系统比单系统拥有更好的空间几何分布;GPS在平面(P)方向内和高程(U)方向上的定位偏差都小于BDS、GLONASS单系统以及GPS/BDS、GPS/GLONASS、GPS/GLONASS/BDS等组合系统,但组合系统在平面(P)方向内和高程(U)方向上的定位结果相比BDS和GLONASS单系统都有所提高;采用原始多普勒观测值测速,GPS、BDS、GLOANASS及组合系统的均方根误差均达到dm*s-1水平。

[1] 杨元喜.导航与定位若干注记[J].导航定位学报,2015,3(3):1-4.

[2] 吴玲,等.GPS/GLONASS/GALILEO多星座组合导航系统研究[J].中国空间科学技术,2009(3):23-28.

[3] 李鹤峰,党亚民,王世进,等.GPS伪距单点定位程序实现若干问题[J].全球定位系统,2013,38(2):33-37.

[4] 张辉,周田,李博,等.BDS/GPS组合系统定位性能分析[J].测绘科学,2014,39(6):18-21.

[5] 唐卫明,徐坤,金蕾,等.北斗/GPS组合伪距单点定位性能测试和分析[J].武汉大学学报(信息科学版),2015,40(4):529-533.

[6] 李鹤峰,党亚民,秘金钟,等.BDS与GPS、GLONASS 多模融合导航定位时空统一[J].大地测量与地球动力学,2013,33(4):73-78.

[7] 何俊,袁小玲,曾琪,等.GPS/BDS/GLONASS组合单点定位研究[J].测绘科学,2014,39(8):124-128.

[8] Information And Analysis Center For Positioning Navigation And Timing.GPS Constellation status [EB/OL].(2015-04)[2017-03-06].https://www.glonass-iac.ru/en/GPS/.

[9] Information and Analysis Center For Positioning, Navigation and Timing. GLONASS constellation status[EB/OL].(2016-06)[2017-03-06].https://www.glonass-iac.ru/en/GLONASS/.

[10]北斗卫星导航系统.发射记录[EB/OL].(2010-01)[2017-03-06].http://www.beidou.gov.cn/xtjs.html.

[11]魏子卿.2000 中国大地坐标系及其与WGS-84的比较[J].大地测量与地球动力学,2008(5):1-5.

[12]刘朝英,陈国,赵齐乐,等.BDS单点测速原理及精度分析[J].大地测量与地球动力学,2014,34(6):114-118.

[13]唐卫明,张先春,惠孟堂,等.基于卡尔曼滤波的北斗伪距单点定位算法研究[J].测绘通报,2016(10):6-8.

[14]余学祥,王坚,刘绍堂,等.GPS测量与数据处理[M].徐州:中国矿业大学出版社,2013.

Precision Analysis of Single Point Positioning Model with GPS/GLONASS/BDS

WANG TAO

(SchoolofGeomatics,AnhuiUniversityofScienceandTechnology,Huainan232001,China)

GNSS pseudorange point positioning speed and there is no ambiguity problem, its principle is simple and easy to realize, so in GNSS data processing, this method is often used. Based on GPS, GLONASS, BDS multi-mode as an example, introduces the existing multi-mode coordinate unification, unified time benchmark problem then introduces the pseudorange point positioning principle and calculation model, based on the Visual Studio2010 platform, written in GPS, GLONASS, BDS multi-mode pseudorange single point positioning procedures and absolute velocity determination. Combined with relevant examples,pseudorange point positioning accuracy and absolute velocity determination were analyzed.

GPS/GLONASS/BDS; pseudo range single point positioning; absolute velocity determination; accuracy

10.13442/j.gnss.1008-9268.2017.03.007

2017-03-06

国家自然科学基金(批准号41474026); 安徽国土资源厅科技项目(编号：2011-K-22，2011-K-18)；安徽理工 大学研究生创新基金(编号：2017CX2056)；淮南矿业(集团)有限责任公司项目(编号:HNKY-JTJS(2013)-28)

P228.4

A

1008-9268(2017)03-0032-06

王涛 (1992-),男,硕士研究生,研究方向为GNSS导航与数据处理。

联系人: 王涛 E-mail: 854554251@qq.com