基于数理统计学的手持GPS测量精度测定

胡涛

(中石化西北油田分公司,新疆 巴州 841600)

基于数理统计学的手持GPS测量精度测定

胡涛

(中石化西北油田分公司,新疆 巴州 841600)

手持GPS是一种依靠GPS卫星进行定位、导航、数据采集的测绘仪器,以其操作简单、便于携带,具有一定的测量精度,在油田的井位踏勘、道路巡检、井位导航、距离量算、概略坐标采集等勘探开发工作中,得到了十分广泛的应用。本文以数理统计学原理和测量误差理论为基础,对手持GPS实际采集的坐标数据进行了分析、处理、计算,求取了手持GPS接收机的定位精度和实际定位误差,为手持GPS的适用范围提供了参考。

手持GPS;白塞尔公式;数理统计;中误差;定位精度

0 引 言

在油田勘探开发工作中,无论是地质物探施工,还是油田开发建设,测绘工作都是一项具有基础性、前瞻性的工作。随着以GPS为代表的卫星定位技术的快速发展,以及在其基础上开发的相关设备产品的日益丰富,手持GPS定位设备以其携带方便,操作简单,已成为油田勘探开发工作中,井位踏勘、道路巡检、井位导航、距离测算、地图概绘等工作中必不可少的设备。随着我国北斗导航卫星定位系统全球布网工作的逐步推进,我国的手持卫星导航产品的开发使用将会更加普及,将会极大地改变和影响人们的生活,提高我国的军事和科技水平。

然而,由于其采用的是以伪距测量技术为基础的绝对单点定位原理[1],与成熟的GPSRTK技术采用的以载波相位技术为基础的相对定位原理相比,有很大的差别,这导致其定位精度与GPSRTK技术厘米级的定位精度相比,还是显得有些大,这就决定了手持GPS仪器只能用来做一些简单的、精度要求不高的测绘工作,从而限制了手持GPS仪器在精密测绘工作中的使用。

那么手持GPS的定位精度到底有多高呢?本文运用了数理统计学原理和测量误差理论,对井位勘定中用来导航的手持GPS定位仪的精度和准确度进行了实际测试和验证。

1 精度的评定指标

大量的测量工作实践表明,对每一客观存在的量,如距离、高差、角度等,在相同的条件下,进行多次重复测量,其结果总是有差异的,这是由测量误差造成的,也就是测量误差是不可避免的。测量中真值与观测值之差称为误差,严格的说应该是真误差,在实际工作中很多真值是不易测定的,因此一般把某一量的准确值与其近似值之差称为误差。误差可分为系统误差、偶然误差和粗差,其中,偶然误差具有数理统计规律,服从正态分布的特征[2],是测量精度评定的主要研究对象。

衡量测量精度的指标有标准差、中误差、相对误差、极限误差等。其中,标准差δ的计算公式为

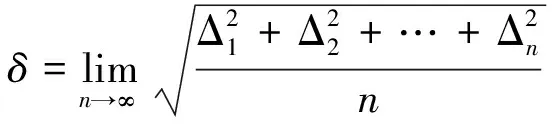
(1)

式中,Δi为单次测量的偶然误差。为了统一衡量在一定观测条件下,观测结果的精度,取标准差作为衡量指标是非常理想的。但是在实际测量工作中,不可能对某一个量作无限次观测,因此在测量中把用有限次观测的偶然误差求得的标准差称为中误差m,用公式可表示为

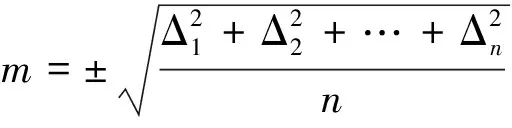
(2)

中误差是测量中最常用的衡量精度的指标,也是计算相对误差、极限误差的基础。

在相同的观测条件下,对某一量进行n次观测,常取n次观测值的算术平均值作为该量的最可靠的数值,称为最或是值。这是因为根据偶然误差的特性,当观测次数无限增大时,偶然误差的理论平均值趋近于零,表达式为

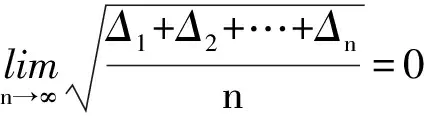
(3)

也就是说此时观测值的算术平均值趋近于该量的真值。同样的在现实工作中,不可能对观测对象进行无限次观测,因此就把有限次观测值的算术平均值作为该量的最或是值。算术平均值与其观测值之差就是观测值的改正值,即

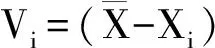
(4)

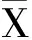
除了少数情况,如三角形的内角和等,在一般情况下,观测值的真值是未知的,那么中误差也就无法用(2)式求得。此时可以用白塞尔公式来计算中误差[3],即用有限次观测值的算术平均值代替真值,相应的改正值代替真误差,计算公式为

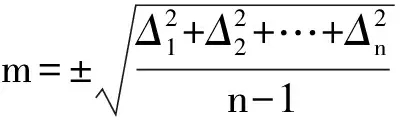
(5)

式中: vi为改正值;n为观测次数。从(2)式和(5)式对比可以看出,除了用改正值代替真误差外,观测次数由n变为(n-1),这是因为在真值未知的情况下,则有一次观测值是必要的,其余(n-1)次是多余观测,这也是统计学中样本标准差[4]的计算公式,其根本原因是样本标准差或中误差是对标准差的无偏估计。因此,n和(n-1)是分别代表真值已知和未知两种不同情况下的多余观测数。本文测定计算手持GPS测量精度运用的就是白塞尔公式。

2 手持GPS定位精度测定方法

测定手持GPS接收机的定位精度,就是通过手持GPS接收机采集同一观测位置的大量数据,用数理统计学原理和测量误差理论,对这些数据进行分析、处理、计算,从而求得手持GPS接收机的定位精度。

为了引入外部对比参考,测定实际的定位误差,测定应在一个已知坐标的测量控制点上进行。由于手持GPS定位采集的坐标只是观测值,其真值是未知的,这样也就无法求得每一个观测值的真误差,因此只能采用大量观测值的平均值作为真值的最佳估值,用改正值代替真误差,最终采用白塞尔公式(5)式计算手持GPS接收机的定位中误差。再用平均值这个真值的最佳估值与测量控制点已知坐标对比,计算出实际定位误差。从而最终完成对手持GPS接收机定位精度和实际定位误差的评估。

采集数据时,应保持手持GPS静止,待初始化完成,卫星接收正常,信号稳定后,开始采集数据。为保证采集数据的一致性,手持GPS接收机的参数设置应与已知测量控制点成果保持一致,这主要包括参考椭球、坐标系统的选择,坐标转换参数、中央子午线、坐标轴加常数的设置等工作。

观测点的选择应符合GPS观测的一般要求,周围应没有大功率电磁辐射体,没有反射电磁波强烈的地物,卫星信号没有高大地物遮挡,保证卫星信号接收正常,以尽可能的将外在因素对定位精度的影响降到最低,使最终结果能尽可能真实地反映手持GPS接收机的定位精度。

3 实例验证

测试采用台湾国际航电股份有限公司生产的GPSMAP 60CSx型手持GPS接收机,该手持GPS接收机为测量外业经常使用的型号,性能稳定。仪器的坐标系、中央子午线、假东、假北及坐标转换参数等各项设置,均经过反复检查核对,保证了观测采集的测试数据与已知控制点坐标成果的一致性。

测试前先选定了一个已知控制点。该控制点观测卫星条件较好,周围地面开阔,在高度截止角为15°的空间区域内,没有遮挡物;周围200 m范围内,没有大功率无线电发射装置和高压输电线[5],没有反射电磁波强烈的水面、玻璃建筑等地物,多路径效应影响较小。

测试开始前先给手持GPS更换了电量充足的电池。开机后先等上几分钟,待接收机初始化完成,卫星信号稳定后,再在已知控制点上,保持手持GPS处于静止状态,开始采集坐标数据,每隔半分钟采集一个坐标数据,采集20个数据为一组。为保证采集的数据具有代表性,采集时间分别选择在8点、10点、12点、16点、20点,共采集了 5组,总计100个坐标数据,手持GPS观测采集的坐标点位分布如表1所示。

最后将采集的100个坐标数据导入电脑,先求取平均值,用平均值这个真值的最佳估值与测量控制点已知坐标对比求差,计算出实际定位误差。然后运用白塞尔公式(5)计算其中误差。由于数据量大,计算可以采用Excel表格提供的 “VAR()函数”,该函数是用来计算基于给定样本方差的,对其结果进行二次开方,就是白塞尔公式,从而简化计算过程。手持GPS定位中误差和定位误差计算结果如表2所示。

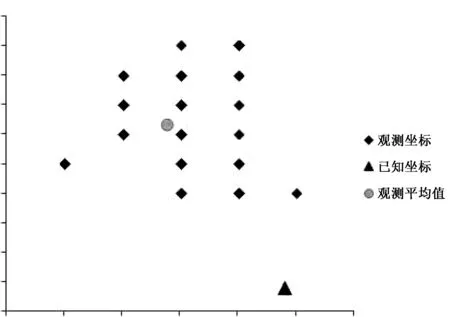
图1 手持GPS观测采集的坐标点位分布

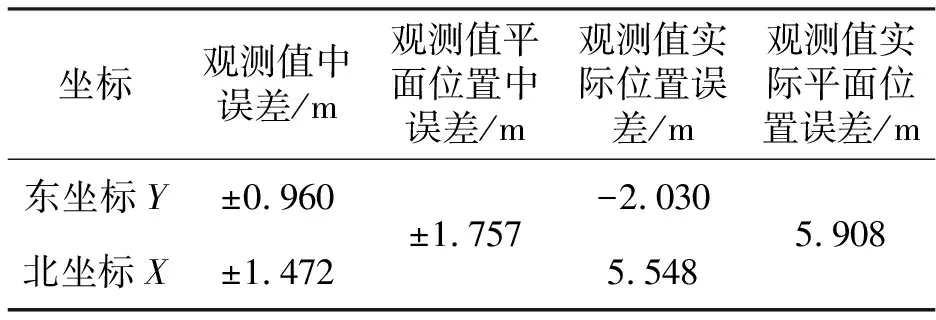
表1 手持GPS定位中误差和定位误差计算结果

4 结束语

实际定位测试表明,GPSMAP 60CSx型手持GPS接收机的静态绝对定位中误差约在±2 m左右,实际定位误差约在±6 m左右,与GPS RTK厘米级的定位精度相比,远不在一个量级。而在油田井位测定施工中,相关规范规定井口的实际测定精度不低于0.02 m,定位误差不超过0.5 m,可见该类手持GPS接收机不可用来油田井位测定施工,只能用来导航、位置粗略定位、坐标粗略估计等测绘精度要求不高的工作。对于其他型号的手持GPS接收机实际定位精度和定位误差的测定,具有一定的借鉴参考意义。

[1] 张勤,李家权.GPS测量原理及应用[M].北京:科学出版社,2011:73-74.

[2] 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M]. 武汉:武汉大学出版社,2007:6-12.

[3] 马江洪.概率统计教程[M].北京:科学出版社,2008:116.

[4] 潘正风,程效军，成枢，等.数字测图原理与方法[M].2版.武汉:武汉大学出版社,2007:42-50.

[5] 中华人民共和国国家质量监督检验检疫总局、中国国家标准化管委员会. 全球定位系统(GPS)测量规范GB/T18314-2009[S].北京:中国标准出版社,2009:4-5.

Measurement of Handheld GPS Measurement Accuracy Based on Mathematical Statistics

HU Tao

(SinopecNorthwestOilfieldBranch,Bazhou841600,China)

Handheld GPS is a GPS satellite positioning, navigation, data acquisition and mapping instruments, with its simple operation, easy to carry, with a certain degree of measurement accuracy, in the oil field wells survey, road inspection, well location navigation, distance Calculation, rough coordinate acquisition and other exploration and development work, has been a very wide range of applications. Based on the theory of mathematical statistics and measurement error, this paper analyzes, processes and calculates the coordinate data collected by handheld GPS, and obtains the positioning accuracy and actual positioning error of handheld GPS receiver, which is the applicable range of handheld GPS Provided a reference.

Handheld GPS; White Searle formula; mathematical statistics; medium error; positioning accuracy

10.13442/j.gnss.1008-9268.2017.03.018

2017-03-10

P228.4

A

1008-9268(2017)03-0087-03

胡涛 (1987-),男,工程师,国家注册测绘师,主要从事卫星定位、工程测量技术在石油勘探开发领域的应用和研究工作。

联系人: 胡涛 E-mail: hutao.xbsj@sinopec.com