基于窄带信号抽样的信号高效传输

魏建+孙祥娥

摘 要： 奈奎斯特抽样定理是对频率宽度有限长的模拟信号进行数字化处理的重要定理之一，而对于这类频宽有限信号中的特殊信号，即窄带信号而言，依据奈奎斯特抽样定理对信号进行抽样时会出现一些新问题。在指出窄带信号存在原因的基础上，以抽样信号的频谱不混叠为根本对窄带信号进行抽样，并使其与按照奈奎斯特定理抽样后的信号进行比较分析。借助通信原理相关知识予以在信道传输中进行分析，得出信号经窄带信号抽样定理处理后的优势所在。

关键词： 窄带信号； 窄带信号抽样； 奈奎斯特抽样定理； 频谱分析； 通信系统传输

中图分类号： TN911.7?34 文献标识码： A 文章编号： 1004?373X（2017）17?0064?03

Signal efficient transmission based on narrowband signal sampling

WEI Jian， SUN Xiange

（College of Electronics and Information Engineering， Yangtze University， Jingzhou 434020， China）

Abstract： The Nyquist sampling theorem is one of the important theorems for digital processing of analog signals with finite frequency width， but has some new problems while sampling the narrowband signal in the finite bandwidth ones. On the basis of the reason that the available narrowband signal exists the problems， the narrowband signal is sampled by taking the non?aliasing frequency spectrum of the sampling signal as the foundation， and compared with the signal after sampling according to the Nyquist theorem. The signal in channel transmission is analyzed by means of related knowledge of communication priciple to get the advantages of the narrowband signal processed with sampling theorem.

Keywords： narrowband signal； narrowband signal sampling； Nyquist sampling theorem； spectral analysis； communication system transmission

0 引 言

信号在各种物理媒体的信道传输过程中，为实现信号的无线传输与频分复用，需通过调制方式将不同的基带信号搬移到不同的频段上，使多路信号在通过同一信道传输时彼此互不干扰。现代通信系统具有成本低、抗干扰能力强和远距离通信等优点，因此受到人们的重视并且传输频带也相对较窄。在此基础上，本文通过窄带信号的抽样来分析其在信道中的传输过程。

1 窄带信号抽样定理

1.1 窄带信号产生

在通信系统传输过程中，频分复用是一种非常重要的解决一条信道同时传输多路信号的技术。它是按照频率来划分信道的复用方式，主要可在模拟信号和数字信号的多路传输过程中被应用。对需要在信道中传输的数字信号，尤其像语音信号或者特定数据信号，皆属于低频宽的信号，此类信号要通过信道直接传输，在传输过程中会产生不可逆的衰减。由于信道中噪声的存在，又会受到噪声的干扰。为了解决这种情况，需要把低频信号的频谱搬移到高频处以适应在信道中的传输。

考虑信号：

（1）

式中：是一个低频的带限信号；正弦信号的频率远大于其最高频率正弦信号的初相位为现假设它为一常数。

显然，的频谱是的频谱在轴上做移位之后的叠加，即：

（2）

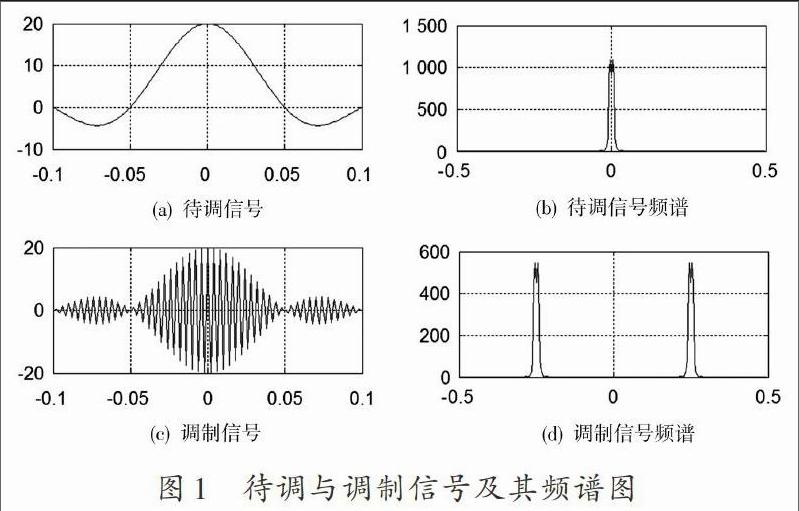
假定，如图1（a）所示，幅频响应如图1（b）所示，那么，如图1（d）所示。可以看出，仅在的范围内有值，其余部分皆为零。的有效带宽为远小于其中心频率把这样的信号称为带通信号或窄带信号，其形式如式（1）所示。显然是由信号被一快变的正弦信号经过调制所得，如图1（c）所示。称为待调信号（modulating signal）或基带信号，为载波信号（modulated signal），自身的变化反映在载波信号的包络上。所以，式（1）的调制方法称为幅度调制（Amplitude Modulation，AM）[1?2]。

1.2 抽样定理

假定一调制信号为：

（3）

分别采用抽样率为10 Hz和20 Hz的冲激脉冲序列对其进行抽样处理，通过Matlab绘图观察抽样后的信号频谱同原信号频谱之间的联系与区别。此信号为一带通信号，其频谱宽度约为7 Hz，再对其以10 Hz进行抽样处理得到的信号为：

（4）

而以20 Hz抽样处理得到的信号为：

（5）

通过Matlab作图可以看出原信号频谱及两次抽样处理后信号的频谱如图2和图3所示。

从图2及图3可以看出，以频率10 Hz抽样得到的信号频谱出现了交叠，故无法把原信号从抽样信号中恢复出来，而以频率为20 Hz抽样的信号却仍可以恢复出原信号。值得注意的是，这里满足抽样信号条件的抽样频率20 Hz并不是原信号中最高频率的两倍，它满足的是另一个抽样定理——带通抽样定理。当频带较窄时，也称窄带抽样定理。endprint

一个带通信号或窄带信号，其频带为由于最低频率不是从零频率开始的，且奈奎斯特频率并不需要达到此时要求的抽样频率的最低值为：

（6）

式中：是不超过的最大整数；。即则抽样频率是在之间。化简式（6），得可知，满足的抽样频率即可从抽样信号中恢复原信号[3?6]。

2 结果分析

将式（3）所示函数调到中心频率约为4 096 Hz，分别用满足窄带信号抽样定理频率为1 kHz和满足奈奎斯特抽样定理频率为10 kHz的频率进行抽样处理，原信号频谱和不同频率抽样后的频谱图如图4所示。

由图4可知，在频率同为-8～8 kHz的范围内，当抽样频率为10 kHz时，在很多频率点上并没有信号出现，在传输过程中会浪费很多频段资源。在抽样频率为1 kHz时，抽样信号出现在各相应频率点上。而且，采用窄带抽样定理进行抽样的数据量变为奈奎斯特抽样定理处理时的在0～8 kHz范围内，抽样频率与1 kHz时的频率之比为而与10 kHz时的比值为。由此可以得出：在传输同一路信号时，采用窄带抽样定理抽样后进行传输的信号可以节省更多频带资源。

从图4中抽样频率为1 kHz的波形与原信号频谱的图形对比中可以看出，除了对应的频率点上有相同谱线外，在其余频点上也有大量谱线，显然，这些信号并不是在通信系统中要传输的信号。在传输之前，将抽样后的信号通过一个带通滤波器，该滤波器會保留基带内的频谱分量，从而得到要传输的信号频谱。滤波后的频谱如图5所示。

在通信系统中，信道容量和信道带宽具有正比的关系，带宽越大，容量越大。当信道容量一定时，对高频窄带信号采用大于两倍的最高频率进行抽样，频率将会更高。此时，信号在传输过程中带宽远超出了信道带宽，其高次谐波会被信道滤除，通过该信道接收到的信号就会没有发送的质量好。对于上述要传输的信号，当其最高频率在10 GHz及以上的范围来说，此方法进行抽样传输后的频率将在20 GHz及以上，在硬件上实现相当困难，对于通信系统来说，不但数据量更大，同样也产生了较大的浪费与利用的不合理。

当信号经过窄带抽样定理抽样处理之后，在容量一定的信道中传输时，信号在此过程中会节省很多信道资源。此时，就能充分利用节省下来的时间资源或信道频带使得信道的利用率提高。这样就可以结合频分复用技术按频率来划分信道。划分后，信道带宽会被分成多个互相不重叠的频段，每路信号会占据其中一个子通道，并且各通道之间要留有未被利用的频带以便进行分隔，防止信号混叠。然后，在接收端采用适当的带通滤波将多路信号分开，进而恢复出所需的信号[7?11]。

通过以上分析，可见窄带抽样定理在对特定信号抽样后，在通信系统传输过程中有更多优势。

3 结 语

本文通过图形介绍了窄带信号，并对奈奎斯特抽样定理与窄带信号抽样定理做了相应比较，通过与通信系统结合的讨论，简要分析了窄带信号抽样在信道传输中的应用优势。在教学过程中，授课教师对于窄带信号抽样理论的介绍相对较少、相应书籍也不是很多，在学生所学知识的理论中并未形成相应脉络体系。基于此，本文相应的研究讨论是必要的，不仅为相关专业的同学拓宽思路，也为高校老师提供了相关的教学方向。

注：本文通讯作者为孙祥娥。

参考文献

[1] 李永全，杨顺辽，孙祥娥.数字信号处理[M].武汉：华中科技大学出版社，2011.

[2] 胡广书.数字信号处理：理论、算法与实现[M].北京：清华大学出版社，2012.

[3] MITRA S K，余翔宇.数字信号处理：基于计算机的方法[M].北京：电子工业出版社，2012.

[4] 张德丰.Matlab在电子信息工程中的应用[M].北京：电子工业出版社，2009.

[5] 周先春，石兰芳.数字信号处理[M].北京：清华大学出版社，2015.

[6] 向强，黄勤珍.线性正则变换域的窄带信号表示及其抽样理论[J].云南大学学报（自然科学版），2015，37（4）：491?499.

[7] 樊昌信，曹丽娜.通信原理[M].北京：国防工业出版社，2012.

[8] 王友村.现代通信原理[M].成都：电子科技大学出版社，2013.

[9] 戴绍港，居建林，许晓荣，等.通信原理实验[M].北京：经济科学出版社，2013.

[10] 崔健双，王丽娜，郑红云.现代通信技术概论[M].北京：机械工业出版社，2014.

[11] 鞠巧慧.通信工程传输技术的应用[J].中国新通信，2012，14（11）：53?54.endprint