Matlab在数字信号处理课程教学中的应用

程俊

摘要：数字信号处理是一门理论性强、教学难度大、学习难度大的学科，Matlab具有强大的信号处理功能。本文将Matlab引入到教学中，给出了利用DFT分析连续非周期信号频谱的分析实例，通过仿真图形不但提高了学生的学习兴趣，帮助学生更好理解原理和相关概念，还能提高学生分析问题和解决问题的能力。

关键词：数字信号处理；DFT；频谱分析

中图分类号：TP37 文献标识码：A 文章编号：1009-3044（2016）09-0241-02

Application of MATLAB in Digital Signal Processing Teaching

CHENG Jun

（College of Physical and Information Science， Hunan Normal University， Changsha 410081， China）

Abstract： Digital signal processing is a subject with strong theory and great difficulty in teaching and learning. Matlab has powerful signal processing function. This paper gives an example of using DFT to analyze the spectrum of continuous non periodic signals.Analyzing examples by Matlab simulation in teaching not only can improve the students' interest in learning， help students better understanding the principles and related concepts， and still can improve students' ability analysis to analyze and solve problems.

Key words： digital signal processing； DFT； spectrum analysis

《数字信号处理》是通信专业和电子技术专业的专业基础课。该课程介绍了数字信号处理的基本理论、基本概念和基本方法，主要讨论了时域离散信号和系统的时域和频域分析、离散傅里叶变换及其快速算法、IIR和FIR数字滤波器的设计。使学生掌握离散系统处理连续信号，利用DFT对信号进行谱分析，数字滤波器的设计和实现。为进一步学习有关通信、电子技术等方面的课程打下良好的基础。

本文以采用DFT分析连续非周期信号的频谱为教学实例，对Matlab在数字信号处理教学中的仿真应用进行探讨。由于连续非周期信号x（t）的频谱是连续函数，需要对其进行时域和频域的离散化处理以近似分析对应的频谱，掌握整个过程中出现的现象是该门课程的一个难点内容，通过Matlab仿真将频谱分析现象运用图形来讲解，便于学生理解其物理含义，从而达到事半功倍的教学效果。

1 混叠现象

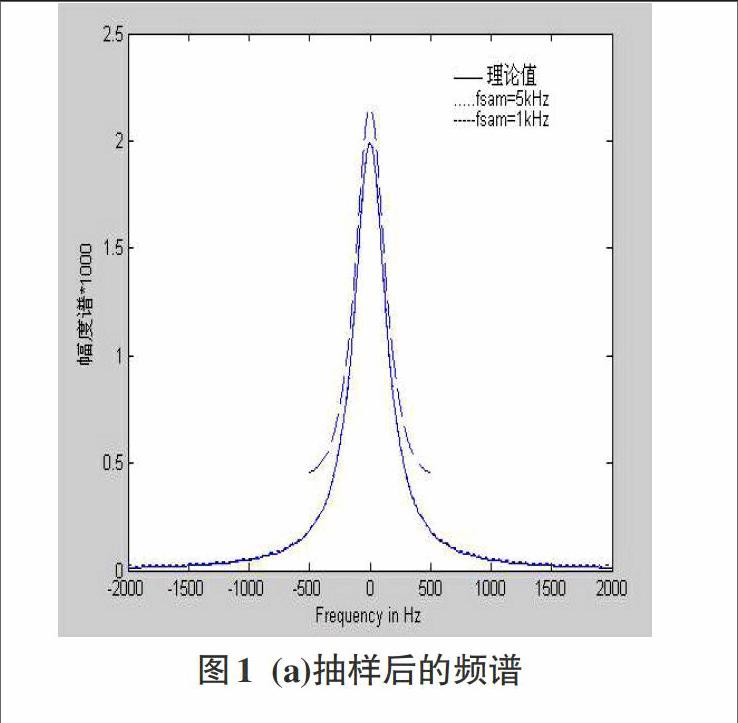
对于连续信号x（t），DFT计算出的频谱是连续信号频谱周期化后在[0，2π）范围的抽样值，如果抽样频率不满足抽样定理，或者连续信号不是带限信号，就会出现信号频谱的混叠。 对连续信号[xt=e-1000t]，在10-5精度下，x（t）为fmax=2000Hz的带限信号，若取时间段t≤|0.05|s，Δt=5*10-5时间间隔时，可在Matlab中产生平滑的时域波形和频谱图，对该连续信号进行时域抽样，分别选择抽样频率为fsam=1kHz、5kHz，所得频谱如图1（a）所示。从图可见fsam=1kHz时出现严重频谱混叠，fsam=5kHz时没有出现频谱混叠。

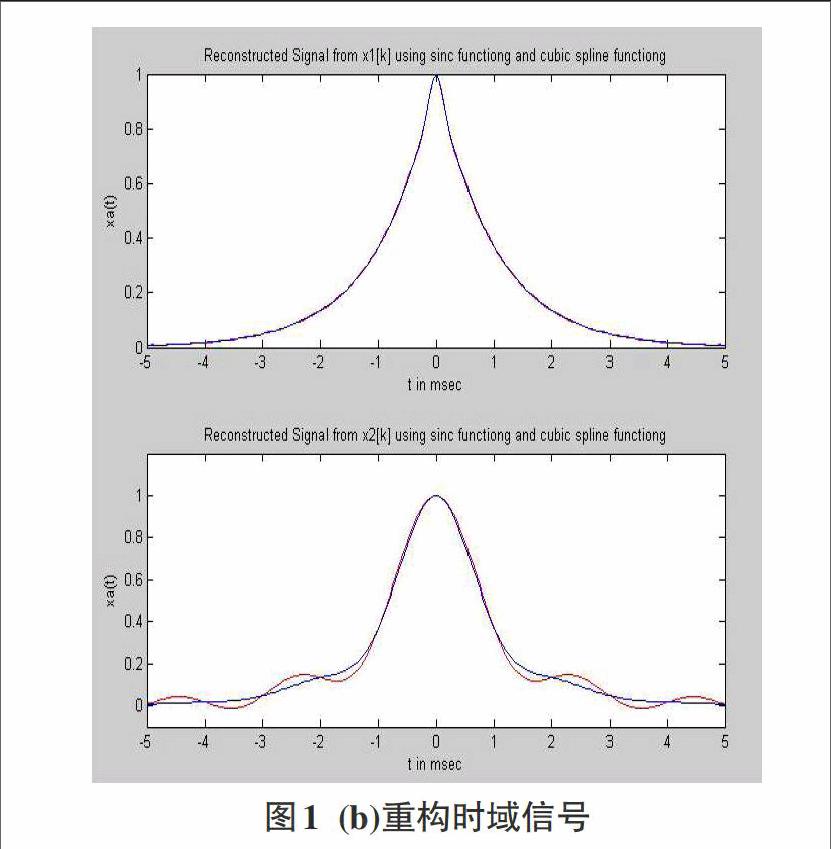
对x（t）信号采用fsam=5000Hz、1000Hz频率抽样后的时域离散序列x1[k]和x2[k]分别采用sinc和3次样条内插函数重构x（t），如图1（b）所示，对于x1[k]采用sinc函数和3次样条函数时重构信号与原信号的最大误差分别为0.0363和0.0317，说明重构的精度相当不错。对于x2[k]采用sinc函数和3次样条函数时重构信号与原信号的最大误差分别为0.1852和0.1679，说明重构的误差很大，这时已不能从x2[k]中恢复原信号x（t）了。

2 泄漏现象

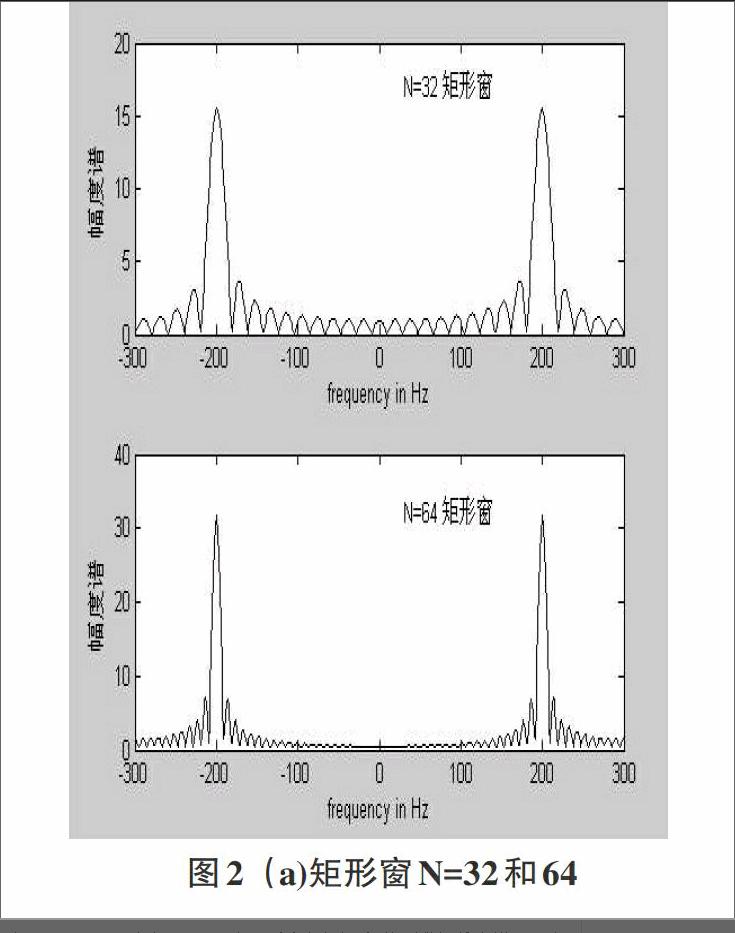
如果连续信号x（t）时域无限长，则离散化后的序列x[k]也是无限长，需要进行加窗截短处理后成为有限长序列才能进行DFT分析。考虑x（t）=cos2πft，f=200Hz，以抽样频率fsam=600Hz对该信号进行抽样，并分别用N=32和64的矩形窗分别进行截短，将N点截短信号补0后做512点DFT分析，结果如图2（a）所示。从图可见，加窗处理对频谱分析造成了两个影响：频谱中出现了多余的频率分量，称为频率泄漏。谱线变成了具有一定宽度的谱峰，谱峰的宽度与信号的长度成反比。针对影响，比较图2（a）中N=32和64点情况，增加窗口的长度N并不能减少频率泄漏，必须通过选择不同的窗函数来改善。图2（b）采用汉明窗对无限长序列进行N=32和64点的截短处理再补零做512点的DFT变换，可见旁瓣泄漏大大减少了。对于影响，可通过增加窗口的长度N来减少主瓣宽度，从而改善频率分辨率。考虑x（t）=cos2πf1t+0.15cos2πf2t，f1=100Hz，f2=150Hz，以抽样频率fsam=600Hz对该

信号进行抽样，分别用矩形窗和汉明窗取N=25和50点进行截短，通过补零进行512点的

DFT结果如图3所示。可见矩形窗旁瓣泄漏大，难以检测幅度较小的频率分量f2，因而采用汉明窗，当N=25时，频率分辨率低，仍难以检测f2，当N=50时，频率分辨率提高，能很清楚显示出幅度较小的频率分量。3 栅栏现象

对连续信号进行时域抽样和加窗处理后得到有限长序列，利用N点的DFT计算有限长序列的频谱也是长度为N的序列，实际上是周期化后的连续频谱在[0，2π）范围内的等间隔采样。由于频谱是离散序列，因而无法反映抽样点之间的频谱细节，导致了栅栏现象。栅栏现象是利用DFT对连续信号谱分析中无法克服的现象。考虑x（t）=cos2πf1t+cos2f2t， f1=100Hz， f2=120Hz，以抽样频率fsam=600Hz对该信号进行抽样，用长度为30点的矩形窗进行截短处理，通过补零进行32点和128点的DFT结果如图4所示。通过比较可知补零减小了频谱分析时的谱线间隔，使计算出的频谱出现更多的细节，随着补零的增加，显示的频谱信息也更多。

在教学过程中，通过Matlab设计具体的仿真实例，运用图形化的方式来讲解抽象的理论知识和技术理论，使学生更好的理解数字信号处理课程中的概念和设计方法，从而提高学生的应用能力。

参考文献：

[1] 陈后金，薛健，胡健. 数字信号处理[M]. 高等教育出版社，2008.

[2] 楼顺天，李博菡. 基于MATLAB的系统分析与设计[M]. 西安电子科技大学出版社，2001.

[3] 高西全，丁玉美. 数字信号处理[M]. 西安电子科技大学出版社，2008.