镜反射下雷达目标检测性能

杨 勇， 肖顺平， 张文明

(国防科技大学 电子信息系统复杂电磁环境效应国家重点实验室， 湖南 长沙 410073)

镜反射下雷达目标检测性能

杨 勇， 肖顺平， 张文明

(国防科技大学 电子信息系统复杂电磁环境效应国家重点实验室， 湖南 长沙 410073)

镜反射使得雷达接收目标信号起伏变化，从而影响着雷达目标检测性能。本文分析了镜反射下雷达对不同Swerling起伏目标的检测性能，推导给出了不同镜反射系数下雷达对不同Swerling起伏目标的检测概率数学表达式，仿真分析了多种镜反射场景下雷达目标检测性能以及镜反射对雷达目标检测性能的影响。

雷达；检测；镜反射；检测概率；Swerling起伏目标

0 引言

雷达检测低空目标时面临着多径散射干扰。多径散射包括镜反射和漫反射两种，当反射表面较平坦时，多径散射以镜反射为主。在镜反射条件下，经地、海面反射的目标回波与目标直达波叠加在一起，使得雷达接收到的目标回波信号时而衰减、时而增强，从而导致雷达检测性能不稳定。分析镜反射下雷达目标检测性能可为雷达低空目标检测方法研究提供指导。

镜反射模型有两种：第一种模型考虑一路反射信号，地球表面为一平面，地面平坦并具有良好导电性，镜反射系数幅度为1、相位为-π；第二种模型考虑三路反射信号，地球表面为一曲面，地面具有一定粗糙度，镜反射系数随场景变化而变化。

文献[1]采用第一种镜反射模型，分析了镜反射条件下雷达对非起伏目标和瑞利起伏目标的检测性能。

在文献[1]的基础上，文献[2]考虑地球曲率和地面粗糙度，进一步分析了不同镜反射系数下雷达对非起伏目标和瑞利起伏目标的检测性能。

文献[3]着重分析了镜反射对雷达检测非起伏目标的影响。

文献[4]对比分析了镜反射条件下和自由空间中雷达采用不同M/N检测器在不同虚警概率下的目标检测性能。

到目前为止，不同镜反射系数下雷达对不同Swerling起伏目标的检测性能对比分析工作尚未见报导。

本文推导得到了不同镜反射系数下雷达对不同Swerling起伏目标的检测概率数学表达式，并对镜反射条件下雷达对不同Swerling起伏目标的检测性能进行了仿真对比分析。

1 功率传播因子概率密度函数

雷达收发共用同一天线，雷达镜反射示意图如图1所示。图1中，lr、lt、R分别表示AO、BO、AB路径长，θd、θr分别为直达波、镜反射回波与波束中心指向之间的夹角。镜反射条件下，雷达接收信号由四路回波组成：AB-BA、AB-BOA、AOB-BA、AOB-BOA。假定BA和BO方向的目标RCS相同，则雷达接收的目标回波信号可表示为

(1)

其中，A0、φ分别为直达波信号幅度和相位，Gt(θ)、Gr(θ)分别为发射和接收天线在θ方向的增益，ρ为镜反射系数幅度，α=α1+α2，α1=2π(lt+lr-R)/λ，λ为波长，α2为镜反射系数相位。

图1 镜反射示意图

在此，定义镜反射幅度传播因子为[5]

v=A1/A0

(2)

其中，A1为镜反射条件下雷达接收目标信号幅度。根据式(1)和式(2)，镜反射幅度传播因子可表示为

(3)

雷达低仰角观测时，θr≈θd，于是，Gt(θr)≈Gt(θd)、Gr(θr)≈Gr(θd)。因此，式(3)可化简为

v=|[1+ρexq(jα)]2|=1+ρ2+2ρcosα,

v[(1-ρ)2,(1+ρ)2]

(4)

通常情况下，α1服从[0,2π]均匀分布[8]。由于α1为常数，因此，α服从[0,2π]均匀分布。由此可推导得到v的概率密度函数为

(5)

定义镜反射功率传播因子μ为镜反射下雷达目标回波功率与无镜反射时雷达目标回波功率之比，则μ=v2，μ的概率密度函数为

μ[(1-ρ)4,(1+ρ)4]

(6)

2 检测概率

本节首先推导无镜反射时雷达接收信号功率概率密度函数，基于此，然后再结合镜反射功率传播因子概率密度函数推导镜反射条件下雷达检测概率数学表达式。

无镜反射时，雷达接收信号可表示为

(7)

无镜反射时，雷达接收信号幅度z=|x|的概率密度函数为[9]

(8)

其中，I0(*)表示0阶第一类修正贝塞尔函数。

用杂波与热噪声总功率β2对雷达接收信号功率进行归一化，归一化后的雷达接收信号功率t=z2/β2，根据式(8)，容易推导得到t关于s的条件概率密度函数为

(9)

对于起伏目标和非起伏目标，t关于瞬时信杂噪比的条件概率密度函数数学表达式相同。但是，对于非起伏目标，其瞬时信杂噪比S是一个未知常数；而对于起伏目标，其瞬时信杂噪比是一个随时间变化的未知变量。下面我们推导雷达对Swerling起伏目标接收信号功率的概率密度函数。

对于Swerling起伏目标，无镜反射时，令其平均信杂噪比为S0，其瞬时信杂噪比为ζ，瞬时信杂噪比的概率密度函数记为f(ζ)。镜反射条件下，Swerling起伏目标的瞬时信杂噪比为ξ=μζ，其概率密度函数可表示为

(10)

将式(6)代入式(10)，可得ξ的概率密度函数为

(11)

根据式(11)可得，H1假设下，归一化后的雷达接收信号功率概率密度函数为

f(t)==∫0∞f(t/ξ)*f(ξ)dξ

(12)

根据式(12)，可计算得到雷达对Swerling起伏目标单脉冲检测概率为

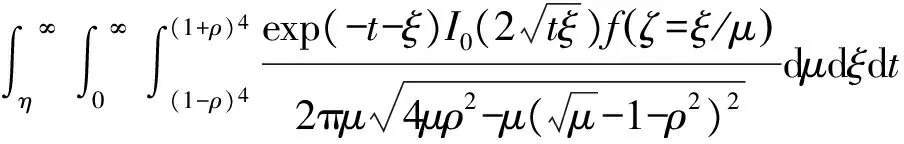
(13)

对于非起伏目标，无镜反射时，雷达单脉冲检测概率为[10]

(14)

对于非起伏目标，镜反射条件下，雷达单脉冲检测概率为[2]

(15)

其中，Q(‘，’)为Marcum Q函数。

对于Swerling I/II型目标，无镜反射时，其信杂噪比概率密度函数为

(16)

无镜反射时，雷达对Swerling I/II型目标单脉冲检测概率为

(17)

将式(16)代入式(13)，可得镜反射下雷达对Swerling I/II型目标单脉冲检测概率为

(18)

对于Swerling III/IV型目标，无镜反射时，其信杂噪比概率密度函数为

(19)

无镜反射时，雷达对Swerling III/IV型目标单脉冲检测概率为

(20)

将式(19)代入式(13)，可得镜反射下雷达对Swerling III/IV型目标单脉冲检测概率为

(21)

值得一提的是，式(17)、式(20)分别是式(18)、式(21)中f(μ)=δ(μ-1)时的特例。对于式(18)、式(21)，较难得到其解析表达式，为此，我们采用扩展辛普森公式通过数字积分来计其值[11]。

令式(17)或式(20)中的S0=0，可得雷达单脉冲检测的虚警概率为

Pf=exp(-η)

(22)

3 仿真结果与分析

令Pf=10-3、ρs=0.9，通过理论推导和蒙特卡洛仿真得到的有、无镜反射时雷达对Swerling I/II型目标检测概率如图2所示。其中，蒙特卡洛仿真次数为10000次。从图2中可以看出，理论推导结果与仿真结果相吻合，从而验证了第2节中理论推导的正确性。同时可以看出，镜反射使得雷达检测低信杂噪比Swerling I/II型目标的性能提高；镜反射使得雷达检测高信杂噪比Swerling I/II型目标的性能降低。

图2 雷达对Swerling I、II型目标的检测概率

令Pf=10-6、ρs=0.9，仿真得到有、无镜反射时雷达对不同Swerling起伏目标的单脉冲检测概率如图3所示。由图3同样可以看出，镜反射对雷达目标检测既有利也有弊，镜反射有利于雷达检测低信杂噪比目标，镜反射不利于雷达检测高信杂噪比目标。无论镜反射是否存在，大多数情况下，雷达对非起伏目标的检测性能最好，其次分别是Swerling III/IV型目标和Swerling I/II型目标。另外，图3表明，镜反射降低了雷达对非起伏目标、Swerling III/IV型和Swerling I/II型目标检测性能之间的差异。

图3 雷达对不同Swerling起伏目标

图4给出了不同镜反射系数下雷达对不同Swerling起伏目标的检测性能。从图4中可以看出，雷达对低信杂噪比目标的检测概率随着镜反射系数的减小而降低，雷达对高信杂噪比目标的检测概率随着镜反射系数的减小而增大。由此可推测，随着镜反射系数的减小，镜反射条件下雷达目标检测概率将逐渐接近于无镜反射时的雷达目标检测概率。

图4 不同镜反射系数下雷达对Swerling起伏目标的检测性能

4 结语

本文推导给出了镜反射条件下雷达对不同Swerling目标检测概率数学表达式，并通过仿真分析了镜反射下雷达对不同Swerling起伏目标的检测性能。结果表明，镜反射有利于雷达检测低信杂噪比目标，不利于雷达检测高信杂噪比目标；镜反射缩小了雷达对不同Swerling起伏目标检测性能之间的差异；镜反射对雷达检测性能的影响效果随着镜反射系数的减小而减弱。

[1] S. R. Wilson, and B. D. Carlson. Radar detection in multipath[J]. Knebworth, IEE Proceedings of Radar Sonar and Navigation，1999，146(1)：45-54.

[2] J. Yeonsoo, L. Hyeongyong, and Y. Dongweon. Multipath effect on radar detection of nonfluctuating targets[J]. New Jersey, IEEE Transactions on Aerospance and Electronic Systems，2015，51(1)：792-795.

[3] R. J. A. Tough, C. J. Baker, and J. M. Pink. Radar performance in a maritime environment: single hit detection in the presence of multipath fading and non-Rayleigh sea clutter[J]. Knebworth, IEE Proceedings F，1990，137(1)：33-40.

(杨 勇等文)

[4] S. Watts, C. J. Baker, and K. D. Ward. Maritime surveillance radar part 2: detection performance prediction in sea clutter[J]. Knebworth, IEE Proceedings F, 1990，137(2)：63-72.

[5] 杨勇，王雪松，张文明，肖顺平. 多径环境下海面低空目标检测技术研究[J]. 青岛，电波科学学报. 2011，26(3)：443-449.

[6] Y. Yang, D. J. Feng, X. S. Wang, and S. P. Xiao. Effects of K distributed sea clutter and multipath on radar detection of low altitude sea surface targets[J]. Knebworth, IET Radar, Sonar and Navigation, 2014，8(7)：757-766.

[7] D. K. Barton. Low-angle radar tracking[J]. New Jersey, Proceedings of the IEEE, 1974，62(6)：687-794.

[8] E. Daeipour, W. D. Blair, and Y. Bar-Shalom. Bias compensation and tracking with monopulse radars in the presence of multipath[J]. New Jersey, IEEE Transactions on Aerospance and Electronic Systems, 1997，33(3)：863-882.

[9] M. W. Long. Radar Reflectivity of Land and Sea[M]. 3rd ed., London: Artech House, 2001.

[10] A. M. Richards. Fundamentals of Radar Signal Processing[M]. New York: McGraw-Hill Companies, 2005.

[11] 叶其孝，沈永欢. 实用数学手册[M]. 北京：科学出版社，1999.

Radar Target Detection Performance in Specular Reflection Circumstance

YANG Yong， XIAO Shun-ping， ZHANG Wen-ming

(StateKeyLaboratoryofComplexElectromagneticEnvironmentEffectsonElectronicsandInformationSystem,NationalUniversityofDefenseTechnology,Changsha410073，China)

Specular reflection interfere with radar

target signal, which influences radar target detection performance. This paper analyzed radar detection performance for Swerling fluctuation targets in specular reflection circumstance. Radar detection probability and false alarm probability for Swerling fluctuation targets with various specular reflection coefficients are derived. Radar detection performance for Swerling fluctuation targets in various specular reflection circumstances are analyzed by simulations.

radar； detection; specular reflection; detection probability, Swerling fluctuation targets

2016-07-09;

2017-01- 05

国家自然科学基金资助(61501475，61490692)

杨 勇(1985-)，男，博士，讲师，主要从事雷达低空目标检测与抗干扰技术研究，E-mail：youngtfvc@163.com

TN95

A

1008-0686(2017)03-0110-05