倾倒滑塌式崩塌预警判据研究
2017-09-08王延平
王延平
(山东理工大学 建筑工程学院,山东 淄博 255049)
倾倒滑塌式崩塌预警判据研究
王延平
(山东理工大学 建筑工程学院,山东 淄博 255049)
通过对倾倒滑塌式崩塌变形破坏机制的分析,确定控制崩塌失稳的关键块体及其破坏过程.根据莫尔库伦准则建立崩塌极限状态下的平衡方程,依据断裂力学理论确定临界裂缝深度,并以此确定极限平衡方程中崩塌的自重,再由极限平衡方程反推确定崩塌裂缝的临界宽度,最终建立崩塌裂缝临界宽度预警判据公式.通过对比物理模拟试验结果和崩塌裂缝临界宽度判据计算结果表明:裂缝临界宽度判据公式的计算结果与试验模型破坏时监测到的临界裂缝宽度值接近,裂缝临界宽度预警判据是合理可行的,可以作为倾倒滑塌式崩塌的监测预警的重要依据.
崩塌;预警判据;应力强度因子;极限平衡方程
倾倒滑塌式崩塌是崩塌灾害中较常见的类型之一.典型的倾倒滑塌式崩塌如:重庆南川区甑子岩崩塌[1]、贵州凯里龙场崩塌[2]等.因为崩塌灾害失稳具有突发性和隐蔽性的特点,所以崩塌灾害的准确预测预报难度较大.国内外学者对崩塌灾害的预测预报做了大量的研究.王尚庆[3]对链子崖危岩体进行监测预报研究,分别应用类比分析、统计分析和因果分析进行预测预报研究,并依据裂缝变形和变形速率的加快,位移曲线斜率加大,突变或者进入加速变形等建立预警判据.伍法权,王尚庆[4]应用卡尔曼滤波法对链子崖危岩体进行预测.尹晖,丁窘辋[5]用时间序列分析方法中的DDS建立预测模型,并又根据灰色理论建立灰色预测模型.胡厚田[6]用信息量统计方法进行危岩崩塌体宏观区段的预测,用模糊综合评判法详细预测危岩崩塌的稳定性.伍岳等[7]应用非连续变形分析( DDA) 方法对链子崖危岩体的两个剖面进行了模拟,并对后期的变形进行了预测.黄志全,王思敬[8]基于摩擦定律,用协同学和分岔理论建立边坡失稳的时间预报协同-分岔非线性预报模型.陈洪凯[9]根据断裂力学分析研究危岩体崩塌的变形破坏机制及其失稳时间的预测预报.田卿燕(2008年)[10], 罗建强[11]用灰色突变理论对危岩崩塌体进行时间预测.国外学者对危岩崩塌的预测预报研究主要集中在地质灾害评估及落石运动轨迹等危险性预测研究,仅少量研究涉及崩塌失稳时间的预测预报.如:U.Glawe, P. Zika[12]根据现场监测数据建立位移时间函数,设定失效阙值预测危岩体失稳时间.Osasank S, Staceyt R[13]利用边坡监测雷达建立基于速度倒数法的边坡失稳预测模型(SFPM),模型在加速变形阶段能有效预测崩塌失稳时间.
从国内外学者的研究成果可以看出,崩塌灾害预测预报方法主要是依据变形监测数据的变化趋势建立预测预报模型.本文依据崩塌的变形破坏机制,以极限平衡法建立崩塌极限状态下的临界裂缝宽度预警判据,以期通过另外一个角度探讨崩塌失稳的预测预报方法.
1 倾倒滑塌式崩塌破坏机理
倾倒滑塌式崩塌一般具有陡倾坡外的节理面,在差异风化或者外界扰动作用下,底部往往形成岩腔或内凹坡形,坡体在重力偏心作用下产生弯矩作用,并在弯矩作用下坡体上部后缘拉应力集中,当拉应力超过边坡岩体抗拉强度时,岩体被拉开形成拉裂缝.随着崩塌底部的持续风化和扰动,崩塌体后部裂隙逐渐加深,当崩塌具有足够的高度时,即裂隙发展到一定的深度,崩塌在重力作用下沿斜截面剪断底部岩体失稳破坏,如图1所示.其变形破坏过程为倾倒—剪断—失稳.具有此种破坏方式的崩塌称为倾倒滑塌式崩塌.

图1 倾倒滑塌式崩塌破坏模式概念图
2 基于极限平衡方程的预警判据
2.1 崩塌极限状态下的极限平衡方程
倾倒滑塌式崩塌由于受裂缝的切割,崩塌体与母岩分离.崩塌体的重量由崩塌底部岩体承担,随着裂隙向深部发展,崩塌体自重逐步增大,崩塌体底部岩体承受的竖向压力也逐步增大.当崩塌体自重超过底部岩体抗压强度时,底部岩体在压力作用下沿斜截面剪切破坏.因为崩塌体底部岩体一侧临空,所以崩塌底部岩体的受力状态可以近似看作为单轴竖向受压.
根据莫尔-库伦准则,崩塌底部岩体破坏面的抗剪强度为
τf=c+σ·tanφ
(1)
式中:σ为破坏面法向应力;C为内聚力;φ为内摩擦角.
当破坏面上的剪应力τ大于等于τf时,岩体破坏,即
τ≥τf
(2)
根据岩石力学基本理论,破坏面上的正应力和剪应力分别为
(3)

(4)
因为崩塌底部岩体主要承受崩塌体的压力,且崩塌底部岩体侧面临空,所以崩塌底部岩体的最大主应力和最小主应力分别为

(5)
σ3=0
(6)
式中:G为崩塌体的自重;b为崩塌体稍宽度.
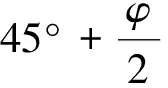
把式(5)、式(6)代入式(3)、式(4),并整理得
(7)
把式(7)代入式(2)得
整理得
(8)
当满足式(8)时,崩塌体剪断底部岩体失稳滑塌.
2.2 裂缝临界宽度预警判据
因为倾倒滑塌式崩塌的后缘拉张裂缝是在弯矩作用下形成,在不考虑重力作用下的裂缝扩展,倾倒滑塌式崩塌的裂缝发育可近似简化为弯矩作用下的裂缝扩展,在失稳前崩塌体的此种受力特征与断裂力学中自相平衡集中力矩作用于端部的受力特征相似,如图2所示.
裂缝的应力强度因子KI,由下式确定:
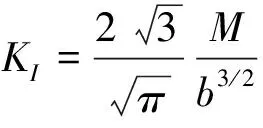
(9)
M=G·e
(10)
式中:M值为弯矩;b为崩塌体岩体厚度;e为偏心距;G为崩塌体自重.把式(10)代入式(9),整理得
(11)

图2 自相平衡集中力矩作用于端部
崩塌体在弯矩作用下后缘被拉开,崩塌体与母岩分离.根据断裂力学I型断裂位移公式,裂缝宽度为位移值,即
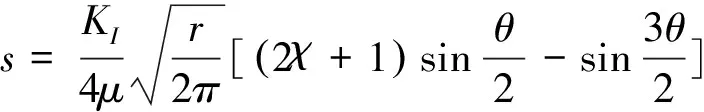
(12)
(13)
式中:KI为应力强度因子;μ为剪切模量;r为半径,即裂缝深度;θ旋转角;ν为泊松比;E为弹性模量.
式(12)的坐标原点在裂缝端部;坐标轴X轴与裂缝平行,且方向与裂缝发育方向一致;r为裂缝深度;因为裂缝顶部与X轴方向相反,则θ=180°,由式(12)可得
(14)
式(11)代入式(14)整理得
取式(13)第二项代入上式整理得

(15)
由于倾倒滑塌式崩塌重心位置约为崩塌体中部,则由重力偏心作用产生的弯矩作用于崩塌体中部,则式(15)中裂缝深度r和裂缝宽度s为崩塌中部位置处的深度值和裂缝宽度值,而实际崩塌顶部裂缝深度和裂缝宽度可近似为2r和2s.假定崩塌顶部位置裂缝深度和裂缝宽度分别为L和S,代入式(15)整理得
(16)
则由式(8)可推得倾倒滑塌式崩塌失稳时后缘裂缝临界宽度值:
(17)
简化得
(18)
式中:γ为岩体容重;C为内聚力;μ为剪切弹性模量;φ为内摩擦角,χ由式(13)确定;p为岩体抗压强度;b为崩塌体厚度.
如果崩塌底部有凹腔时,崩塌底部岩体最大竖向应力将增大,则下部岩体在较小的裂缝宽度下可能会失稳破坏,根据式(5)和式(18)可得到由于崩塌底部凹腔引起的裂缝临界宽度减小的折减系数公式

(19)
式中:h为凹腔深度.
3 预警判据的试验验证
3.1 崩塌的物理模拟试验
依据相似性原理进行崩塌物理模拟试验.崩塌物理模拟试验模型的原型为贵州省威宁县猴场镇幺岩脚崩塌[14].幺岩脚崩塌岩性为灰岩,崩塌体高81m,厚约10~13m,其变形破坏机制为倾倒剪切破坏.通过现场取样并进行室内物理力学试验,测定灰岩的物理力学性质,根据相似性原理对崩塌尺寸和物理力学参数进行缩尺(见表1),并建立试验模型,
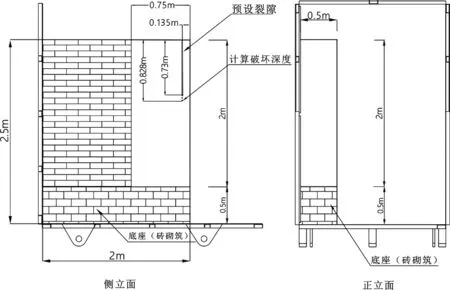
图3 倾倒滑塌式崩塌试验模型

图4 试验模型 图5 破坏后的试验模型
如图3所示.根据试验模型设计砌筑模型,砌筑时预留裂缝深度为73cm,试验模型设计尺寸如图3所示.试验开始前在崩塌底部挖掘凹腔,挖掘深度为8.01cm,如图4所示.
通过调整模型倾斜角度改变模型的力学作用条件.试验时通过定期调整模型倾角逐步增大模型的弯矩,模型最大倾斜角度为14°.模型倾斜角度达到最大值后模型缓慢变形直至失稳.模型破坏断面如图5所示.通过拉绳式位移传感器获取的物理模拟试验的裂缝的位移-时间曲线如图6所示.
表1 原型与模型材料的物理力学特征参数值

密度(ρ)/t∙m-3弹性模量(E)/MPa泊松比抗压/拉强度(σc)/MPa内聚力(C)/kPa摩擦角(φ)/°原型2.75440340.207105.5/10.6160039模型理论值2.75440.340.2071.06/0.111639模型实际值2.211.0560.30.702/0.0828.9648.6

图6 崩塌物理模拟试验的位移时间曲线
根据图6,崩塌物理模拟试验后缘裂缝位移—时间曲线可知:崩塌试验模型破坏时后缘裂缝临界宽度为2.73mm.
3.2 预警判据验证
根据表1确定的相似材料的物理力学参数代入裂缝临界宽度判据公式(18)计算裂缝临界宽度值.因为试验模型在底部进行了挖掘,则根据挖掘深度用公式(19)计算临界宽度折减系数.试验模型材料物理力学参数见表2.
表2 试验模型参数

参数参数值C(内聚力)28.96kPaP(抗压强度)702kPaγ(容重)22kN/m3E11.05625MPaφ48.6°μ0.3偏心距e0.1276m
裂缝临界宽度折减系数计算:
崩塌裂缝临界宽度计算:

则折减后的裂缝临界宽度值:
δ·S=10.5236713×0.259333048=2.7291mm
通过预警判据公式计算得到的临界裂缝宽度为2.7291mm,试验获得的裂缝临界宽度值为2.73mm.计算值与试验模型破坏时的裂缝临界值接近.
4 结束语
以倾倒滑塌式崩塌变形破坏机制为基础,根据崩塌极限状态下的平衡方程推导建立的崩塌裂缝临界宽度预警判据的计算结果与物理模拟试验模型破坏时监测到的裂缝临界宽度值接近,说明以崩塌变形破坏机制为基础建立的预警判据是合理可行的.但是因为验证预警判据合理性的物理模拟试验对实际崩塌进行了高度概化,以及对崩塌力学边界条件进行了高度简化,所以裂缝临界宽度预警判据在实际应用中需要进一步验证.
[1]冯振,陈云霞,李滨,等.重庆南川甑子岩山体崩塌机制研究[J].水文地质工程地质,2016,43(1):50- 56.
[2]董秀军,裴向军,黄润秋.贵州凯里龙场镇山体崩塌基本特征与成因分析[J].中国地质灾害与防治学报,2015, 26(3):3- 9.
[3]王尚庆.链子崖危岩体监测预报初步研究[J].中国地质灾害与防治学报,1994,5(3):79-89.
[4]伍法权,王尚庆.卡尔曼滤波方法在链子崖危岩体变形适时预报中的应用[J].中国地质灾害与防治学报,1996,7(S1):56- 60.
[5]尹晖,丁窘辋.时序预测和灰色预测用于链子崖危岩体定点变形预报的研究[J].中国地质灾害与防治学报,1996,7(S1):49- 55.
[6]胡厚田,崩塌落石综合预测方法的研究[J]. 铁道工程学报,1996,2(50):182-190.
[7]伍岳,王泽民,徐绍铨.非连续变形分析方法在链子崖危岩体变形预测中的应用[J].武汉大学学报(信息科学版),2003,28(05):573-576.
[8]黄志全,王思敬.边坡失稳时间预报的协同-分岔模型及其应用[J].中国科学:E辑,2003,33(S1):94-100.
[9]陈洪凯,唐红梅,王林峰,等. 危岩崩塌演化理论及应用[M]. 北京:科学出版社, 2009.
[10]田卿燕. 块裂岩质边坡崩塌监测预报理论及其应用研究[D]. 长沙:中南大学,2008.
[11]罗建强, 傅鹤林, 郭少华. 崩塌的灰色-突变预测[J]. 采矿技术,2007,7(4):29-30.
[12]GLAWEU,PZIKAZ,ZVELEBILJ,etal.TimepredictionofarockfallintheCarnicAlps[J].QuarterlyJournalofEngineeringGeology, 1993,26:185-192.
[13]OSASANKS,STACETYTR.Automaticpredictionoftimetofailureofopenpitmineslopesbasedonradarmonitoringandinversevelocitymethod[J].InternationalJournalofMiningScienceandTechnology, 2014(24): 275-280.
[14]张维顺,孙赤,王茜.威宁县猴场镇幺岩脚崩塌机制研究[J].甘肃水利水电技术,2013,49(11):30- 33.
(编辑:刘宝江)
Topple-sliding rockfall warning criterion research
WANG Yan-ping
(School of Civil and Architectural Engineering, Shandong University of Technology, Zibo 255049, China)
Through the analysis of the failure mechanism of toppling collapse, the key blocks controlling the collapse and the failure process are determined. According to the M-C criterion, the equilibrium equation under the collapse limit state is established, and the critical crack depth is determined according to the fracture mechanics theory. The critical weight of the collapse in the limit equilibrium equation is determined by the limit equilibrium equation. Critical width judgment formula for collapse crack is established. By comparing the results of the physical simulation test and the critical width criterion of the fracture, it is shown that the calculation result of the critical width criterion of the crack is close to the critical crack width detected when the test model is destroyed, which indicates that the critical width warning criterion is reasonable and feasible, and it could be used as an important basis for the monitoring and early warning of toppling collapse.
rockfall; warning criterion; stress intensity factor; limit equilibrium equation
2017-03-03
王延平,男, wyp@sdut.edu.cn
1672-6197(2017)06-0042-05
P642.21
A
