基于Tracker软件的动量守恒定律的探究性教学策略
2017-09-08赵鲁宁
赵鲁宁 贾 莹
(中央民族大学理学院,北京 100081)
·现代教学技术·
基于Tracker软件的动量守恒定律的探究性教学策略
赵鲁宁 贾 莹
(中央民族大学理学院,北京 100081)
在验证动量守恒定律的传统碰撞实验的基础上,利用视频分析软件Tracker实时捕捉碰撞前后两球的运动情况.通过追踪小球的运动轨迹,生成摆线位置、碰撞前后小球的速度等数据信息,建立动态粒子模型,使碰撞运动直观化、可视化.这种方法便于加深学生对动量守恒定律的理解,促进高中物理动量守恒定律的教学有效性.
Tracker软件;动量守恒;碰撞;视频分析
动量守恒定律是自然界的基本守恒定律之一,在高中物理教学中具有重要的地位.人教版物理教材给出一种悬挂小球碰撞的方法来探究动量守恒定律,但其在帮助学生得出动量守恒定律以及直观有效地认识碰撞运动等方面有待改善.本文拟利用视频分析软件Tracker对录制的悬挂小球碰撞运动视频进行分析,追踪两小球的运动轨迹,生成实时对应的小球位置信息的曲线图和数据,进而总结得出动量守恒定律.通过此种方法可以相对精确地得出动量守恒定律,同时便于学生直观地理解动量守恒定律和碰撞运动,从而提升教学的效率和效果.
1 传统动量守恒定律探究实验的内容及缺点
动量守恒定律基本内容表述为:如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变.[1]在高中物理的教学中,动量守恒定律的探究实验基本都是通过对碰撞过程的分析来实现,找寻碰撞前后的不变量,总结得出动量守恒定律.

图1 参考实验案例装置图示
在人教版物理教材的动量守恒定律章节中,给出一个参考实验案例,其内容是将两个大小质量相同的小球A、B悬挂起来,小球A保持静止,拉起小球B后释放,使两球发生碰撞,测量小球B释放时的初始角度和小球A被撞后摆起的角度,进而得出小球A、B碰撞前后的速度,最终总结出动量守恒.[1]实验装置如图1所示.
使用这种方法时,对角度的测量存在一定的困难.教师用书给出的建议是使用一块上面固定着白纸的木板,将其放在两个小球发生碰撞的平面后,描画出碰撞前后小球的位置,从而得出小球拉起和摆起的角度.[2]但这种方式有以下一些缺点.
(1) 需要多次碰撞才能相对准确描画,时间花费较长.
(2) 数据获取误差较大,由于使用软线悬挂小球,描画时极有可能会影响到小球本身的运动,造成数据误差.另外由于碰撞的过程时间较短,描画时人的反应时间不够,也极易造成误差.
(3) 数据不够直观,数据分析过程较长,不便于学生直观有效的理解.
2 视频分析软件Tracker的优势
Tracker软件是一个建立于开源物理架构下的影像分析与建模的工具,该软件可以广泛应用于物理教学中,主要是通过分析物理实验的视频,追踪视频中所研究的质心或质点的运动轨迹,从而简便高效地得出实验所需的数据.其具有如下特点.
(1) 追踪高效.
该软件可以实现手动和自动的高效追踪,进而得出位置、速度及加速度的图表和数据.同时它还可以对较大物体实现质点追踪,实现交互式图形向量的表示及计算.
(2) 模拟准确.
可建立追踪质心甚至两个系统的运动学、动力学模型,具有独立建模的动画和覆盖多点数据的外部模型,模型覆盖自动同步同时扩展到视频与现实世界进行直观比较.
(3) 视频选择和处理多样.
该软件可以兼容大部分格式的视频(MOV、AVI、FLV、MP4、WMV等),还具有视频滤镜的功能,可调整视频的亮度、对比度和频闪等,通过这些功能来校正失真.
3 Tracker软件在动量守恒定律碰撞实验中的应用实例
3.1 视频的录制
使用Tracker软件进行数据生成及分析,首先需要一段相关的实验视频.本实验使用了数码相机进行录制,也可使用手机、摄像头等摄像设备录制.为了保持镜头位置不变,使用了三脚架对数码相机进行固定.由于视频会受到拍摄场景的距离及角度的影响,空间尺度易发生改变,因此,选择在靠近被测物且能被录入视频的地方放置标准长度单位的标尺,以便于校正物体运动的实际距离.
实验的内容与上文中提到的参考实验案例一致,使用两个悬挂的质量大小一致的小球发生对心碰撞.
3.2 视频的分析
打开Tracker软件,将录制的视频导入.反复播放视频选择视频的起始帧和结束帧,在两小球悬挂静止的两线之间建立坐标轴纵轴,向上方向为正,保证此轴与两线平行且处于两线中间,横轴沿水平方向且略低于小球位置,向右方向为正.以视频录制时放置的标尺为准建立校正杆,校正杆长度为10cm.
依照两小球的形状设定两个质点对象A和B,两质点的质量大小设为相等.设定两小球为追踪目标,软件将自动追踪两目标位置,并实时记录两小球的位置和时间信息.在本实验中需要3种数据:位置角度、速度大小、速度角度.在软件对两目标进行逐帧分析时,要对其进行检查,若出现追踪目标搜索错误的情况应手动进行标记.其软件的界面如图2所示.

图2 Tracker软件界面
3.3 数据及图像的分析
3.3.1 实验得到的小球A、B的位置图和数据表如图3、图4所示.
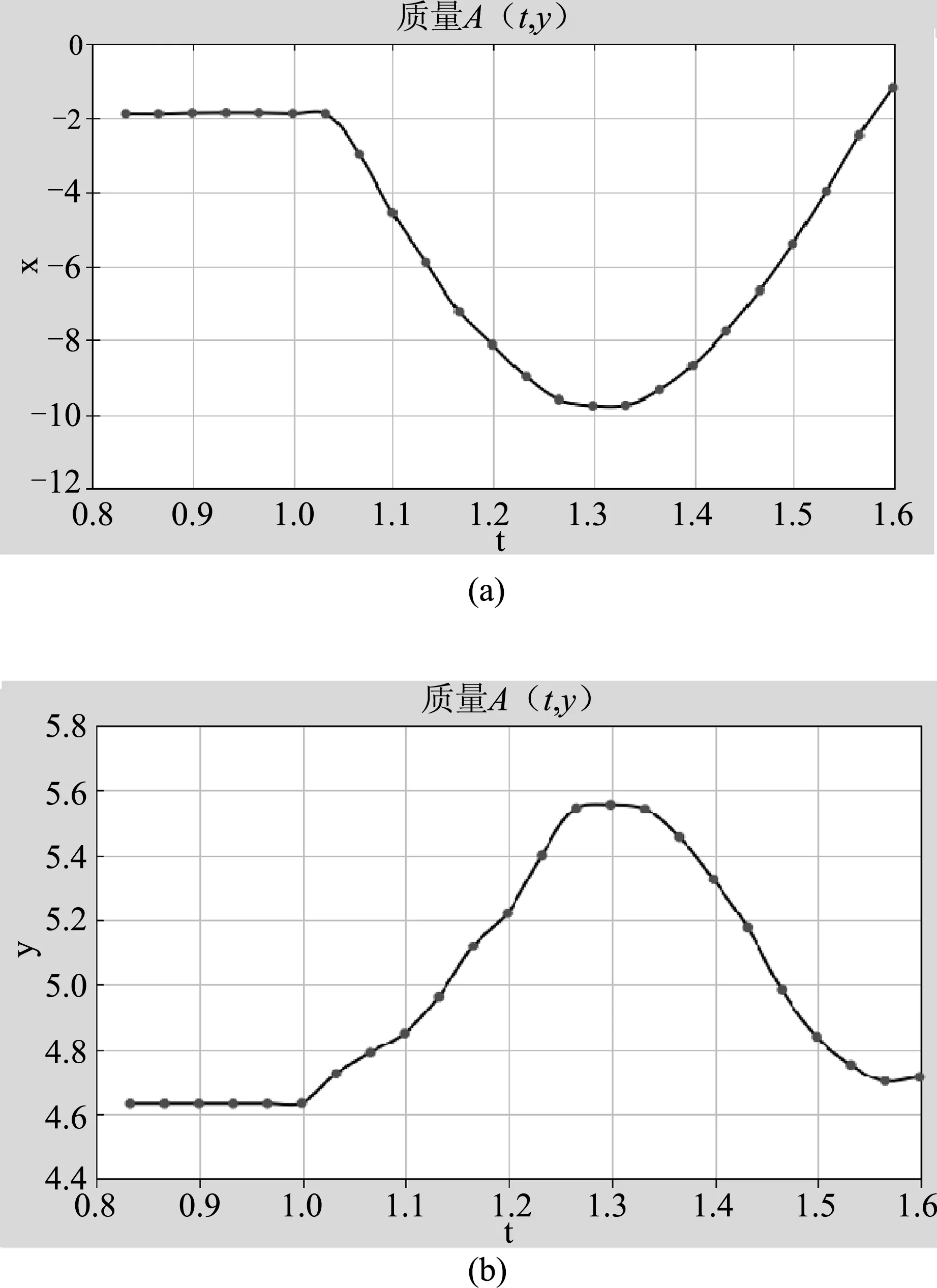
图3 小球A的x坐标和y坐标随时间的变化图
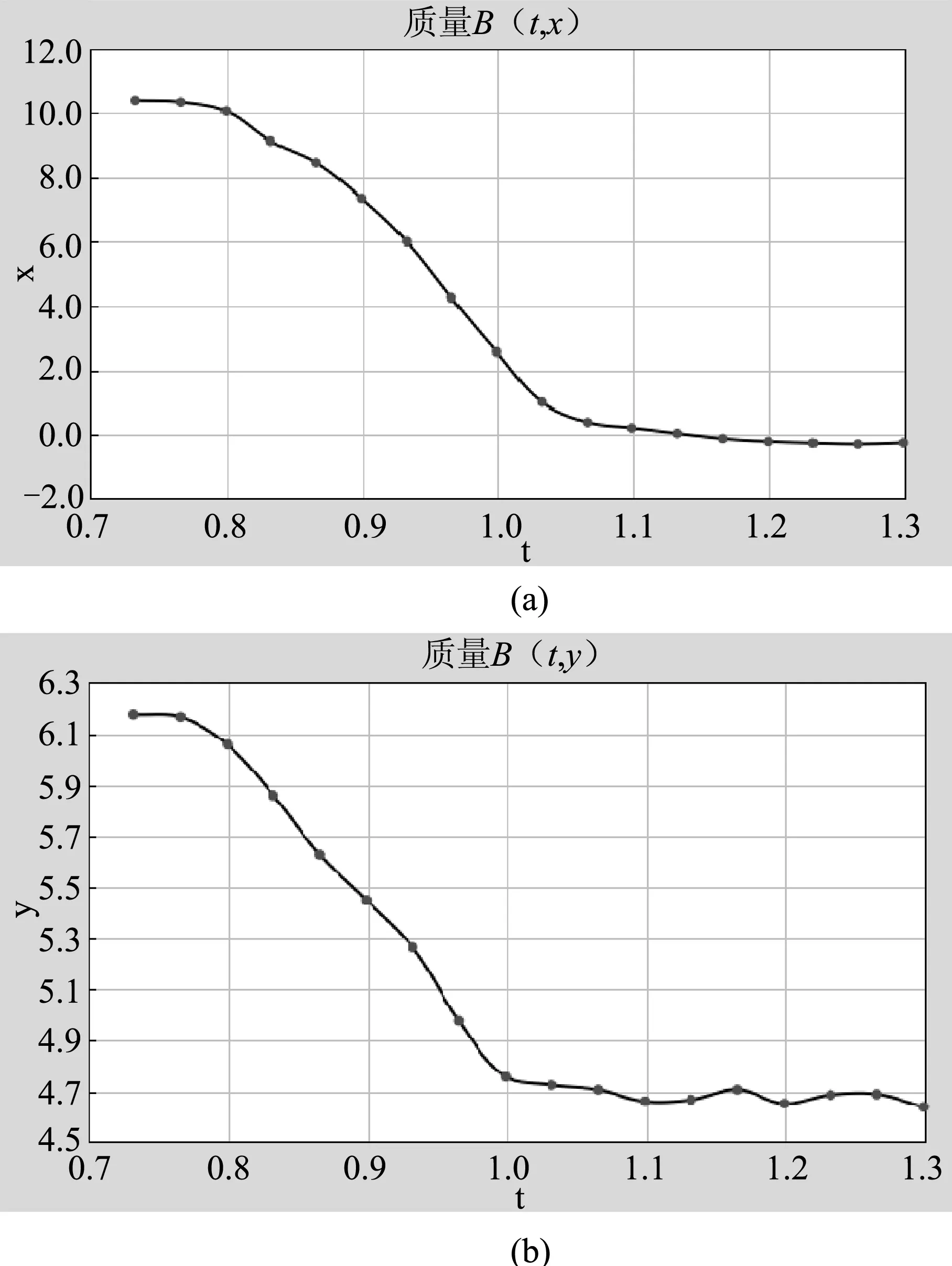
图4 小球B的x坐标和y坐标随时间的变化图
使用Tracker软件进行分析时,可以测得小球A、B的位置角度θA和θB,也就是小球A、B与原点的连线同x轴正向之间的夹角,夹角情况如图5所示.小球A、B的位置角度随时间的变化如表1、表2所示.

图5 小球A、B的位置角度θA和θB图示

表2 小球B的位置角度θB随时间的变化数据表

使用Tracker软件分析时,可以得到运动的小球A、B实时对应的速度大小和角度,如表3、表4所示.速度角度指的是小球A、B的速度方向与x轴正向之间的夹角,当其近似±180°时,可将两球之间的碰撞看成一维对心碰撞.
表3 小球A碰撞前后的速度大小v、速度角度θv数据表

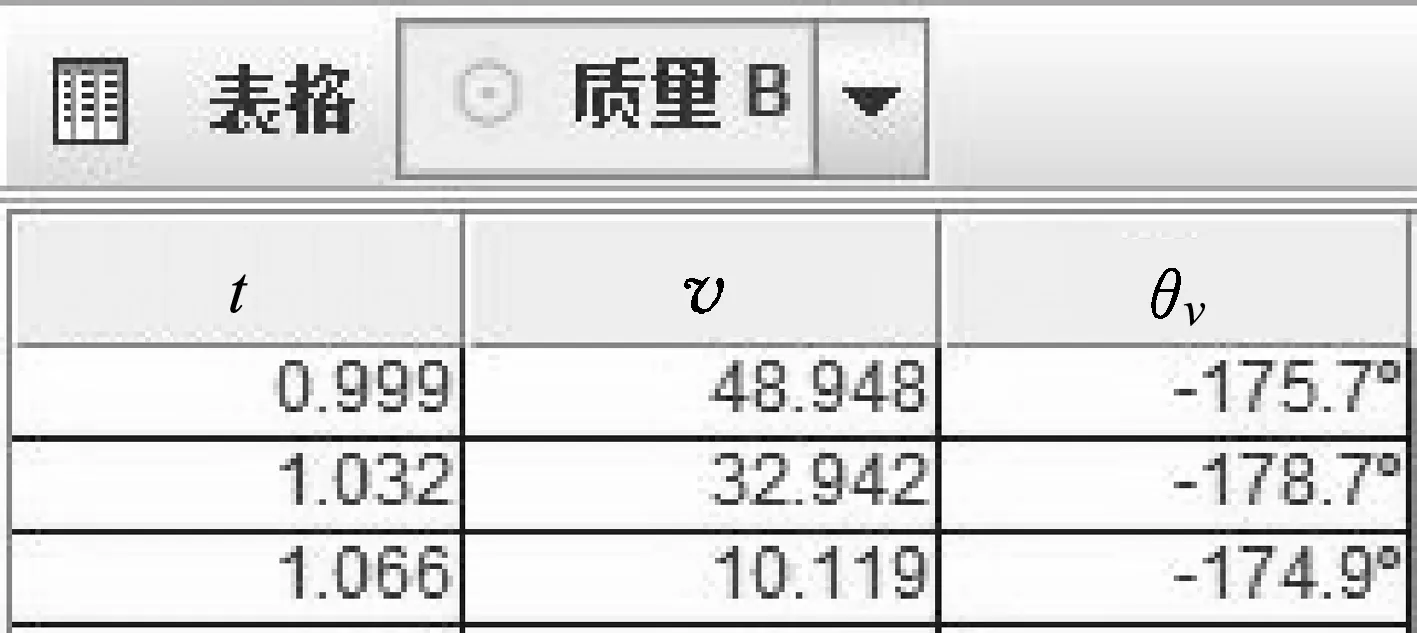
表4 小球B碰撞前后的速度大小v、速度角度θv数据表
3.3.2 数据分析
本实验在分析时主要关注了3个时间点的数据信息:小球B在最高点时,小球A、B发生碰撞时以及小球A被撞至最高点时.
(1) 小球B在最高点时.
由图5(b)可知,当小球B在最高点时,其对应的位置角度θB应该最小,从表2数据中得出此时小球B的摆线角度θB为30.5°.
(2) 小球A、B发生碰撞前后.
小球B发生碰撞前的速度大小为48.948m/s,速度的角度为175.7°;小球B发生碰撞时,速度的大小为32.942m/s,速度的角度为178.7°;小球B发生碰撞后的速度大小为10.119m/s,速度的角度为174.9°.
小球A发生碰撞前的速度大小为0.301m/s,速度的角度为172.5°;小球A发生碰撞时,速度的大小为16.378m/s,速度的角度为176.7°;小球A发生碰撞后的速度大小为40.053m/s,速度的角度为177.7°.
(3) 小球A被撞至最高点时.
由图5(a)可知,当小球A在最高点时,其对应的摆线角度θA应该最大,从表1的数据中得出此时小球A的摆线角度θA为150.4°.
取这3个时间点的数据进行分析,下面将用两种方法验证动量守恒定律.

图6 θA和θB的关系图
首先将小球B在最高点时和小球A被撞至最高点时两个时间点合并在一起进行分析.拉起小球B至最高点时和小球A被撞至最高点时两个时间点合并在一起进行分析,其内容如图
6所示.若要证明动量守恒定律,则要求两个质量大小相同的小球发生碰撞前后,小球B拉起时与y轴之间的角度应该等于小球A被撞至最高处与y轴之间的角度,换句话说,即θA和θB要满足关系θA+θB=180°.
使用Tracker软件分析时可得
θA+θB=150.4°+30.5°=180.9°,
(1)
绝对误差为
Δ=180.9°-180°=0.9°,
(2)
相对误差为
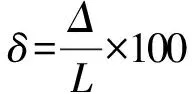
(3)
由于两小球质量大小一致,发生一维对心碰撞后,小球B拉起的角度和小球A被撞起的角度近似相等,可证明动量守恒定律.
第2种方法是通过分析小球A、B发生一维碰撞前后的速度,验证动量守恒定律.
(1) 发生碰撞前,两小球A、B的速度大小相加为48.948+0.301=49.249(m/s).
(2) 发生碰撞时,两小球A、B的速度角度均接近180°,可近似为一维对心碰撞.此时,速度大小相加为32.942+16.378=49.320(m/s).
(3) 发生碰撞后,两小球A、B的速度大小相加为10.119+40.053=50.172(m/s).
通过实验可以看出,发生碰撞前、中、后的两球速度的大小相加近乎相等,可以验证得出动量守恒定律.
4 结束语
利用Tracker软件验证动量守恒定律既可以得到较为准确的实验数据,减小实验误差,又可以通过视频片段中覆盖简单的粒子模型并和视频图像的直观对比加强学生对规律的理解,[3]同时还给予了学生更加多样的数据处理选择.Tracker软件虽然可以播放一些实验视频并能进行分析,但并不能代替实验,[4]因此可以在教师演示探究或是学生合作探究时进行视频录制,起到一定的教学辅助作用,也可提升学生的参与度和积极性.Tracker软件作为一种探究性学习工具,是信息技术和物理教学有效结合的体现.
1 人民教育出版社. 物理选修3-5[M]. 北京:人民教育出版社, 2010:2-8.
2 人民教育出版社. 普通高中课程标准实验教科书物理选修3-5教师教学用书[M]. 北京:人民教育出版社, 2012:5-6.
3 洪炎红,徐晓梅. 基于Tracker软件的平抛运动可视化教学策略[J]. 中学物理教学参考,2015(21):26-29.
4 吴志山. 让真实定量、定格——Tracker软件在物理教学中的应用[J]. 物理教师,2012(07):53-54.
2017-03-04)
