自行车“转弯不倒”问题的研究
2017-09-08黄绍书蒋金团
黄绍书 蒋金团
(1. 六盘水市第23中学,贵州 六盘水 553000; 2. 施甸县第一中学,云南 保山 678200)
自行车“转弯不倒”问题的研究
黄绍书1蒋金团2
(1. 六盘水市第23中学,贵州 六盘水 553000; 2. 施甸县第一中学,云南 保山 678200)
简单介绍对自行车在水平弯道上“转弯不倒”问题的理解上存在的误区与困扰.着重根据刚体转动的力矩平衡,从转动定点悬空的角度,剖析其“转弯不倒”的约束关系,并给出不倒条件下的最大角速度的解析式.
自行车转弯; 刚体转动; 离心力效应; 陀螺效应
1 引言
自行车发明至今已有200多年,关于自行车稳定性问题的研究和讨论同样有同样悠久的历史.特别是自行车转弯时,人和车都总是向弯道的内侧倾斜,人和车组成的系统(以下简称人车系统)的重力作用线不在支撑面上,那么,为什么人车系统不会倾倒呢?这方面已发表的科普文献近百篇,[1]但基本都未离开离心力效应和陀螺效应的观点.
关于自行车稳定性原理的讨论从未停止,并几度掀起热潮,还曾有对流行上百年的离心力效应和陀螺效应的传统观点的怀疑.
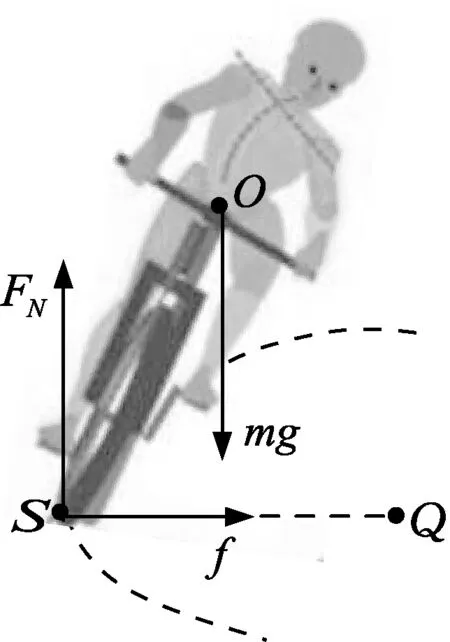
图1
2012年1月,美国科普杂志Discover Magazine评选了2011年全球100个顶尖科学故事.其中“自行车的新物理”荣居第26位.为此,作为最普及的大众简易交通工具的自行车,其困扰公众“转弯不倒”的问题再度热议起来.
2 误区与困扰
如图1所示,自行车在水平弯道转弯时,受到3个力作用,即人车系统的重力mg、路面对车轮的支持力FN及法向摩擦力f.
设人车系统做圆周运动的角速度为ω、轨道半径为r.那么,在竖直方向
FN-mg=0,
(1)
即FN与mg等大反向,合力为0.
在水平方向
f=mrω2,
(2)
即摩擦力f提供转弯所需的向心力.
显然,这一分析过程中,没有考虑人车系统的空间尺度,也没有考虑支持力FN与重力mg之间是非共点力的关系,仅将人车系统的转动考虑成质点的圆周运动.因此,这一分析不能解释转弯“不倒”的问题.
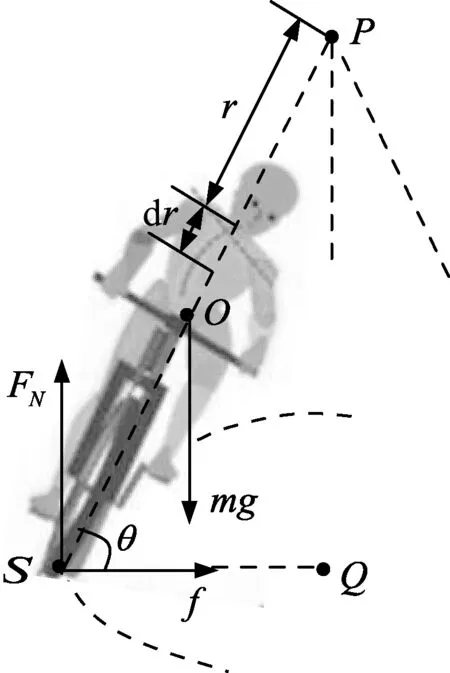
图2
事实上,人车系统是一个相对定轴转动系统.那么,什么力的力矩与重力力矩平衡,使得人车系统转弯“不倒”,而维系着动态平衡状态呢?这就是公众不能释疑的根本性困扰.
3 “不倒”的条件
为了便于讨论,将人车系统简化成刚体.人车系统转弯时,实际是绕某一竖直轴转动,其转动面为一圆锥面,如图2所示.
受力情况与图1一致,不再赘述.设人车系统的重心为O,转动过程中的倾斜角为θ、转动定点(相对)为P,转动轴为过P点的竖直轴,路面支撑动点S与O、P之间的距离分别为l和L.那么,重力mg、支持力FN和摩擦力f对P点的力矩分别为
MG=mg·(L-l)·cosθ.
(3)
MF=FN·L·cosθ.
(4)
Mf=f·L·sinθ.
(5)
由图2可知,支持力FN与重力mg的大小是相等的.在人车系统逐渐倾斜过程中,主动力矩MG和MF将随倾斜角θ的减小而增大,而被动力矩Mf的变化比较复杂,因为摩檫力f的大小与其力臂存在相反的变化趋势.人车系统“倒”与“不倒”,完全决定于这3个力矩之间的约束关系.在人车系统转弯的角速度没有超过最大角速度之前,摩擦力的大小就处在0与最大静摩擦力fm之间的变化范围,且摩擦力的大小由人车系统的转动角速度、转动半径及倾斜角确定,见以下(6)~(11)式的推导.这时,摩擦力矩Mf也随之变化.
(1) 当Mf>MF-MG,即

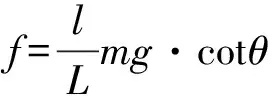

4 最大角速度
人车系统转弯的最大角速度ωm与人车系统对转动定点(相对)P的转动惯量J或回转半径r0有关,[2]同时还与人车系统的最小倾斜角θn有关.
再次将人车系统进一步看成质量均匀分布的细柱型刚体.根据前面设定,人车系统的竖直面总长度应为2l.令人车系统的线密度为λ.在距离图2中的P点为r处,取一长度元dr,则长度元的质量为dm=λdr.因此,人车系统对转动定点(相对)P的转动惯量为

(6)
回转半径为
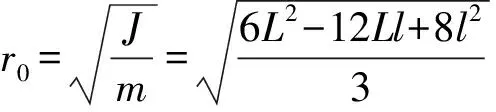
(7)
若设车轮与路面之间的最大静摩擦因数为μm,那么,由图2可知,人车系统转弯的最小倾斜角θn满足
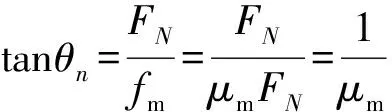
(8)
由于地面对车轮的支持力FN等于人车系统的重力mg,因此人车系统转弯过程中受到路面的最大静摩擦力fm为
fm=μm·mg.
(9)
这一最大静摩擦力就是人车系统转弯时的最大向心力.刚体绕定轴转动时,由于转动惯量的影响,向心力应等效作用于刚体的微分质量集中点.因此,人车系统转弯过程中,最大角速度ωm满足
fm=mr0ωm2cosθn.
(10)
代入各量代数式,化简可得

(11)
5 结语
图2中的转动固定点P以及过该点的竖直轴是相对的,具体要由人车系统的动力学微分方程确定.因此,各式中涉及的路面支撑点S与转动定点P之间的距离L以及转动惯量J、回转半径r0、最大角速度ωm等也都是相对的.
本文的分析还不很彻底,迫切期待同行及专家们的指导和对该问题的进一步深入探讨.
1 刘延柱.关于自行车的稳定性[J].力学与实践,2012,2(34):90-93.
2 哈尔滨工业大学理论力学教研室.理论力学(Ⅰ)[M].北京:高等教育出版社,2009,7(7):259-272.
2017-02-12)
