基于任务可用度的设备维修建模与优化研究

张 帆，王纯贤

(合肥工业大学 机械工程学院，合肥 230009)

基于任务可用度的设备维修建模与优化研究

张 帆，王纯贤

(合肥工业大学 机械工程学院，合肥 230009)

设备故障停机导致的总损失成本包括设备维修成本和生产任务损失成本。为减少多设备混联生产系统中设备故障停机带来的总损失成本，以设备停机总损失成本最小化为目标，综合考虑设备失效率和修复率两方面因素，建立了基于设备任务可用度的维修成本模型。探讨了利用遗传蚁群算法对模型进行优化求解的方法。最后以发动机凸轮机加工线设备为例，验证了所建模型的有效性。

设备停机损失；设备维修模型；任务可用度；遗传蚁群算法

0 引言

设备可用度是可维修设备最重要的性能指标之一，直接影响到生产效率和生产成本。提高设备可用度，降低设备维修成本成为众多学者研究的重要课题。文献[1]对设备的效率成本、维修风险和设备的产能、生产任务等进行了权重分配并建立维修模型。文献[2]对设备的状态值进行了数字记录，以生产系统的运行成本最小化为目标函数，建立设备维修模型。文献[3-4]以设备运行成本最小化为目标，以设备状态值、缓冲库存量为自变量建立设备维修模型。文献[5]研究了预防维修成本的动态性，以设备在固定周期内总维修成本最小为目标函数，以设备可用度和维修计划为约束条件，建立设备维修成本模型。文献[6]以维修时间点与维修程度最优化为目标,在考虑设备可靠性和经济特性的基础上, 定义了各功能部件可靠运行区间的重叠度，以量化各部件维修后可靠性的匹配程度，建立了基于设备可靠运行区间重叠度的维修决策模型。文献[7]以多部件设备为研究对象，以设备维修成本最小化，设备可用度最大化为目标函数，建立设备非周期预防性维修计划。文献[8]以设备可用度为约束条件, 以维修成本最低为目标, 以维修周期为变量, 建立设备维修优化模型。利用Monte Carlo仿真求解目标函数。文献[9]界定了不同维修活动对设备可靠度影响和设备故障率函数关系，设备维修资源和成本的关系，建立以最小总维修费率为目标的分阶段顺序维修经济优化模型。文献[10]基于故障率建立了机床的预防维修模型，通过制定合理的预防性维修周期来降低维修成本。

以上研究中大多仅以维修成本最低为研究目标，考虑维修成本时，缺乏与设备可用度、生产计划、设备生产任务等影响因素的结合。导致研究结果与实际情况相差较大。为此，本文以多设备混联生产系统为研究对象，综合考虑设备可用度和设备生产任务，建立设备维修成本模型，并采用遗传蚁群方法对模型进行求解。以发动机凸轮机加工设备为例，验证维修模型和求解方法的有效性。

1 混联生产系统模型

实际生产过程中，设备布局主要有串联、并联和混联布局方式，通常采用可靠性框图对生产系统进行评估[11]。本文主要考虑串联和并联同时存在的混联形式。

1.1 串联模型

串联生产系统是由串行连接的n台设备构成。生产系统中的任何设备的任意一种失效都会导致整个系统失效。生产系统可靠性框图模型如图1所示。

图1 串联生产系统框图

令R为整个生产系统的可靠度，为第i台设备处于正常运行状态的概率，则：

R=P(X1,X2,…,Xn)

(1)

1.2 并联模型

在并联系统中，设备以并联的方式连接。在这种情况下，单个设备的故障停机不会导致整个生产系统的故障，但会降低生产系统的运行效率。并联系统的框图如图2所示。并联系统的可靠度为：

(2)

图2 并联生产系统框图

1.3 混联模型

混合并联指设备没有特定的构成形式，不是以单纯的串联和并联的方式连接的，可靠性框图模型如图3所示。混联系统的可靠度为：

(3)

图3 混联生产系统框图

2 基于任务可用度指标的维修模型

2.1 维修模型前提

在混联生产系统中，设备维修问题属于多目标优化问题[12]。构建维修模型过程中要综合考虑设备维修方式、维修时间、维修成本、设备可用度、设备生产任务等。本文在构建维修模型时做出以下几点考虑：

(1)维修方式。设备维修分为预防维修和事后维修两种，其中预防维修细分为预防性更换和预防性维修。事后维修细分为最小量维修和完全修复。最小量维修是指对故障设备进行临时性修复，保证其可以继续工作。完全修复是指对设备修复后，设备恢复如新。

(2)维修时间。以统计数据为依据，预测设备故障周期。结合设备的使用状态和生产任务，确定设备维修的周期和灵活性的时间调整。

(3)生产任务。设备维修时机的选择对设备的生产任务会带来很大的影响，将设备的使用状态和实际生产任务相结合做出合理的维修决策更符合制造型企业的效益。生产任务指车间具体的生产计划。

2.2 马尔可夫型维修过程假设

Markov型过程要求系统由相互独立的部件组成，且特征参数服从独立的指数分布，以便利用指数分布的无记忆性求解模型。本文选择混联生产系统为研究对象，混联生产系统中的每台设备为一个独立的构成部分。

设备可用度是指设备在任意时刻能正常工作的概率。基于时间区间和停机类型可分为瞬时可用度、平均开动时间可用度、固有可用度、任务可用度等。任务可用度Am(T0,tf)可以定义为：

(4)

每次失效可以在小于或等于tf的时间内修复，即：

(5)

式中：Fn(T0)为失效时间的分布函数,Fn(T0)-Fn+1(T0)为在时间T0内产生n次失效的概率，(G(tf))n为n次修复中每次修复的时间都小于tf的概率，G(t)修复时间的累积分布函数。

本文以多设备混联生产系统为研究对象，以维修成本最小化为目标，以设备任务可用度为约束条件，以设备维修周期和维修量为自变量，建立设备维修模型。如式(6)所示。

(6)

其中：Ct为设备停机总损失成本，Cw为设备维修成本，Cl为设备停机损失成本。

Cm为设备最小修复成本，Cpm为设备预防维修成本，CPM·R为设备预防性更换成本，Crep为设备事后维修成本。

Cl为设备停机损失成本，Cper为设备单位时间停机成本。

3 基于遗传蚁群算法的模型求解

本文构建的维修模型属于多目标、非线性、动态随机优化问题，模型的搜索空间随生产系统中设备台数呈指数级增加。遗传算法有较强的全局优化能力，能较好地克服过早陷入局部最优解；蚁群算法鲁棒性高，对初始路线要求不高，但对系统的开销较大[8]。

3.1 混合算法思想介绍

为充分利用遗传算法和蚁群算法的优点，本文采用遗传算法与蚁群算法的混合算法来求解最小维修成本问题。首先利用遗传算法得出一个初始解集C，对初始解集的解结果进行标记、比较，得出较优解，并在较优解上留下信息素。把m个蚂蚁放在起始点，起始点置于当前解集中。蚂蚁按照状态概率向下层节点转移，直至完成一次遍历，所有节点置于当前解集中。利用遗传算法的交叉和变异策略，对蚂蚁访问的路径进行交叉和变异操作。如果变异结果得到改善，则保留改善后的较优解，如果变异结果未得到改善，保留原来的解。在蚂蚁完成一次周游后，更新信息素，进入下一次迭代，直到满足迭代结束条件。整个模型的求解流程如图4所示。

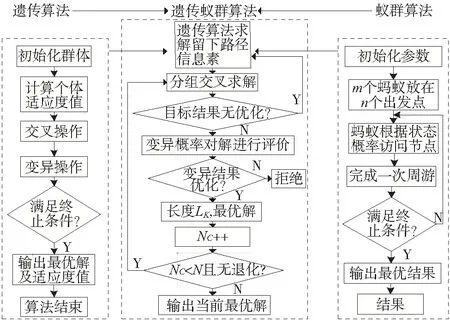
图4 遗传蚁群算法的求解过程

3.2 混合算法的交叉

遗传算法的交叉是把两个父代的部分结构进行替换，从而产生新个体的过程。交叉策略有很多种，本文采用在第二个父代上随机选择一个交叉区域，将第二个父代的交叉区域添加到第一个父代相对应的位置，并删除第一个父代中已经在第二个父代交叉区域中出现过的城市。设有父代M和N，交叉区域为P。如M={2 3 1 6 8}，N={1 6 3 5 9}，P={3 5}。交叉后得M′，M′={2 3 5 6 8}。

3.3 混合算法的变异

变异是对群体中的个体进行基因值的变动。本文采用的遗传蚁群算法的变异指的是蚂蚁的访问路径由C0变异到另一路径C1。在待被访问的n的城市中，随机选择第m(1≤m≤n)个城市，交换路径C0中第m次和第m-1次访问的城市顺序，其它路径保持不变。如：M={2 3 1 6 8}。当m=3时，变异后的路径为M″，M″={2 1 3 6 8}。

3.4 混合算法的求解

在遗传算法得出的初始解集基础上，把初始解抽象成节点[13]。根据变量个数把节点抽象成n层，同一变量的不同解在同一层上，Cij表示第i个变量的第j个初始解。蚂蚁从第一层开始，经过中间节点，到最后一层经过的节点序列就是一个维修方案，序列中各节点代表的费用之和就是该方案的停机损失成本。

(1)状态概率。设τij(t)表示t时刻，节点Cij上的信息量；ηij(t)表示启发式信息，α、β为信息素和启发式信息的权重。t时刻蚂蚁k访问下一节点的概率为：

(7)

allowedk表示在t时刻可以访问的节点集合。

(2)信息素浓度。蚂蚁会在其经过的路径上留下信息素，信息素随时间蒸发，ρ表示蒸发系数。τij(t+n)表示t+n时刻节点Cij上的信息素浓度，Δτijk表示第k只蚂蚁在一次周游中留在节点Cij上的信息素浓度。

τij(t+n)=ρτij+Δτij

(8)

(9)

设Q表示蚂蚁在周游一周留下的信息素总量。一个节点序列中路径越长，单位距离里的信息素浓度就越低。蚂蚁k在节点Cij上留下的信息素浓度Δτijk(t)等于Q/dij。dij等于节点Cij产生的损失成本除以蚂蚁经过该节点遍历完一周后所代表的维修方案的总损失成本。

(3)启发式信息。受目标函数的影响，蚂蚁在访问下一个节点的启发式信息ηij(t)=1/Cij，Cij表示节点Cij的损失成本。

4 实例验证

以某型号发动机凸轮机加工线为例，生产线设计节拍为30s。AF10工位3台加工中心车削凸轮内孔及端面，AF20工位1台磨床磨削凸轮外圆，AF30工位2台设备对凸轮内孔进行激光造型。生产线的整体布局如图5所示，AF10-1表示AF10工位的第1台设备。每台设备的相关参数及设备维修相关成本如表1所示。

图5 凸轮生产线布局图

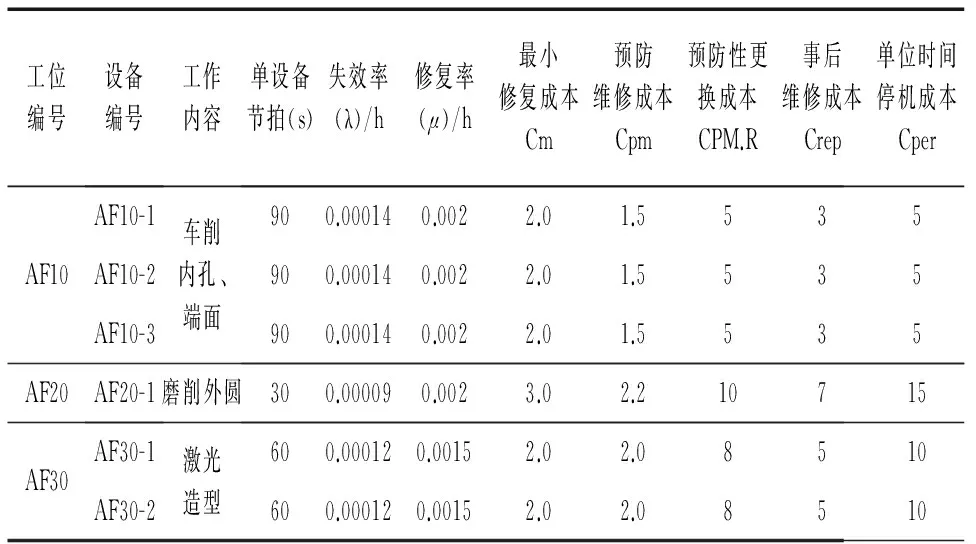
表1 生产线设备相关参数

采用本文的混合算法，以整个生产系统的维修成本最小为目标，以设备任务可用度和设备的失效率和修复率为约束条件，对建立的设备维修模型求解和优化。设备开动率以90%计算，运用Witness模拟720h的运行情况，模拟结果如图6所示：在720h内，生产任务为77760件，T=500时，生产线总维修成本最小为2.29×104元。

5 结论

本文以多设备混联生产线可修复设备为研究对象，建立设备维修模型，利用遗传蚁群算法对模型进行求解，在满足设备任务可用度的前提下对维修模型进行优化，寻找维修周期和维修成本的最佳匹配值。最后以发动机凸轮机加工线设备验证了模型的可行性，为制造业中设备的维修优化提供了更接近实际情况的理论参考。

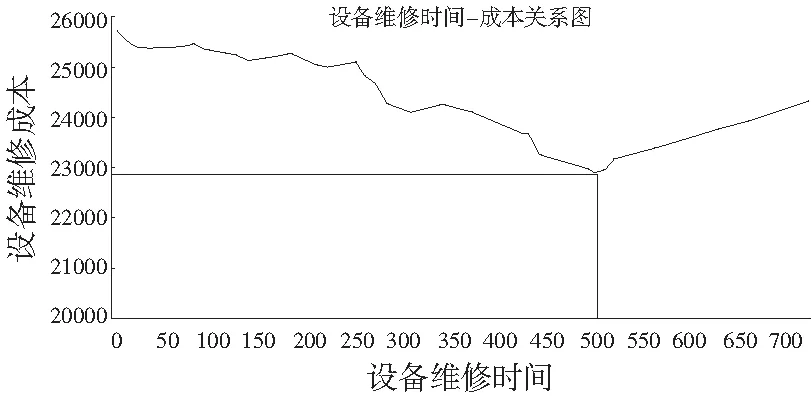
图6 成本模拟求解

[1] Zheng Y, Chen S, Ling H. Efficient multi-objective tabu search for emergency equipment maintenance scheduling in disaster rescue[J]. Optimization Letters, 2013, 7(1):89-100.

[2] Borrero JS, Akhavan-Tabatabaei R. Time and inventory dependent optimal maintenance policies for single machine workstations: An MDP approach[J]. European Journal of Operational Research, 2013,228(3):545-55.

[3] Pavitsos A, Kyriakidis EG. Markov decision models for the optimal maintenance of a production unit with an upstream buffer[J]. Computers & Operations Research,2009,36(6):1993-2006.

[4] Karamatsoukis CC,Kyriakidis EG.Optimal Preventive Maintenance of a Production-Inventory System When the Action of “Idling” Is Permissible.Applications of Mathematics and Informatics in Science and Engineering[M].Springer,2014:217-28.

[5] 宋之杰, 杨志秀, 赵玉忠,等. 可用度及动态维修成本下的维修决策模型[J]. 工业工程, 2014(2):17-22.

[6] 张根保, 王扬, 李冬英,等. 基于可靠运行区间重叠度的设备维修决策模型[J]. 计算机集成制造系统, 2015, 21(3):859-866.

[7] 王灵芝, 徐宇工, 张家栋. 基于设备有效度和可靠度的预防修经济优化模型[J]. 机械工程学报, 2010, 46(4):163-168.

[8] 苏春, 黄茁. 以可靠性为中心的维修成本优化模型及其应用[J]. 机械科学与技术, 2007, 26(12):1556-1559.

[9] 邓超, 段超群, 吴军. 基于设备可靠度的分阶段顺序维修经济优化模型[J]. 计算机集成制造系统, 2016,22(2):568-575.

[10] 王家海, 胡传胜, 张益飞.基于故障率的机床预防性维修周期模型应用[J].组合机床与自动化加工技术,2010(3):43-46.

[11] 龚庆祥. 型号可靠性工程手册(精)[M]. 北京:国防工业出版社, 2007.

[12] 侯文瑞, 蒋祖华, 金玉兰. 基于可靠度的多设备混联系统机会维护模型[J].上海交通大学学报,2009,43(4):658-662.

[13] 吴斌, 史忠植. 一种基于蚁群算法的TSP问题分段求解算法[J]. 计算机学报, 2001, 24(12):1328-1333.

(编辑 李秀敏)

Research on the Equipment Maintenance Model and Optimization Based on Tasks Availability

ZHANG Fan,WANG Chun-xian

(School of Mechanical Engineering, Hefei University of Technology, Hefei 230009, China)

The total costs caused by equipment downtime include equipment maintenance costs and the costs of lost production tasks. In multi-device hybrid production system, to reduce the total costs caused by equipment downtime, with the goal of minimizing the total costs, considering the equipment failure rates and repair rates, a new equipment maintenance costs model was established based on mission availability. Genetic ant colony algorithm was used to solve the optimization model. Finally, an example about engine camshaft was applied to verify the effectiveness of the model.

equipment downtime costs; equipment maintenance model; mission availability; genetic ant colony algorithm

1001-2265(2017)08-0144-04

10.13462/j.cnki.mmtamt.2017.08.038

2016-09-24

张帆(1989—)，男，安徽淮南人，合肥工业大学硕士研究生，研究方向为工业工程，(E-mail)hfutsail@163.com。

TH166;TG506

A