改进的初始种群的遗传算法在柔性车间调度中的应用

牛 琳

(海南医学院 医学信息学院，海口 571100)

改进的初始种群的遗传算法在柔性车间调度中的应用

牛 琳

(海南医学院 医学信息学院，海口 571100)

针对柔性作业车间调度中单纯的遗传算法容易陷入局部陷阱问题，结合柔性作业车间调度的特点，采用模拟退火算法融合遗传算法对调度领域进行了研究。应用模拟退火算法能跳出局部陷阱的能力及克服了遗传算法过早熟的现象，很大程度上降低算法的收敛速度，同时提高了全局的收敛性。基于Matlab2012b软件编程实现混合调度算法，文中仿真实例用混合调度算法，将结果与单纯的遗传算法得到的结果进行比较，证明了混合算法的优势。

遗传算法；柔性作业车间调度；初始种群

0 引言

柔性工作车间调度问题( Flexible Job Shop Scheduling Problem, FJSP)[1]，FJSP也称为工件的排序问题。其分析与研究目的在于企业实现效益最优化—对加工工序进行高效排序，在约束条件下，使得所选择的某个性能指标达到最优状态。遗传算法的鲁棒性好，通用性和计算性能强大，因此较多的用在FJSP的问题中。但在实际应用时由于收敛条件难以保证，所以目前国内外很多文献对遗传算法求解FJSP问题提出了改进策略。例如，欧阳珍，狄瑞坤[2]融入模拟退火算法，提高了种群个体的多样性。柳青红等[3]提出了基于禁忌搜索的遗传交叉算子，改进收敛速度。Zhang H P, Gen M[4-6]提出了一种多阶段遗传算法有效的改进了局部收敛问题。KACEM I，HAMMADI S, BORNE P[7-8]将遗传算法与模糊理论相融合并应用于柔性作业车间调度问题。通过分析遗传算法求解FJSP问题方面已经取得一些成果，但在求解过程中出现的问题还有待于进一步探究改进。文献[9]采用MPGA种群遗传算法结合移民算子对车间调度问题进行了研究。刘韵[10]等采用PSO启发搜索式的粒子群优化算法，解决了柔性车间调度时间问题。文献[11]通过遗传算法结合模糊算法对车间空间的搜索时间和收敛速度进行了改进。

鉴于此，本文在文献[2]的基础上对算法进行改进，将遗传算法和模拟退火算法结合在一起，通过典型的柔性作业车间调度问题，将改进前后的调度结果进行比较分析，调度结果有了一定程度的提高，速度也有了一定程度的缩短，并将混合算法和单纯的遗传算法进行调度最优解的对比，详细的分析了两者收敛代数、调度时间，证明了混合算法的优于单纯的遗传算法。

1 FJSP数学优化模型

柔性操作车间可调度问题通常可简述为：存在N个加工工件，需要用M台机器加工，需加工的每个工件包含多重加工工序，每道工序可以在一台或多台机器上加工，加工时间随机器因素的差异而异同，规定工件的前一道工序未加工后一道工序则不能进行，同一类工件的所有工序之间存在先后顺序；每个工序同一时刻只能在一台机器上加工。问题目标为每重工序需选择最合适的机器，需要在这些工艺约束条件下，调整每一台机器上不相同工件间的加工顺序,使机器加工性能达到最优状态。

1.1 FJSP变量定义

(1)N：工件数量，M：机器数量，n：工序数。

(2)工件集合用数组J表示，J={J1,J2,…,Jj}，Jj为第j个工件，j=1,2，……，N。

(3)机器集合用数组P表示，P={P1,P2,…,Pp}，PP为第p个机器，p=1,2，……，M。

(4)对应工序所用的加工机器为Ppj(1)，Ppj(2)，…，Ppj(n)。则机器的加工顺序矩阵为P：

其中,Ppj(n)：j工件的工序n在机器Pp(p=1,2,…,M)上加工。

(5)加工时间集合用矩阵Tp表示:

其中,Tpj(n)：j工件的工序n的加工时间(在机器Pp上)。

(6)tjp定义为工件j在机器p上的总加工时间。

(7)cjp定义为工件j在机器p上的完工时间。

1.2 调度目标数学模型

目标函数为：在给定的工艺约束条件下进行调度优化，使最大完工时间(makespan)最小，或者最小生产周期，即如何安排加工使得加工所有工件的时间最短；

(1)

约束条件：

cjp-tjp+A(1-ajhp)≥cjh

(2)

cjp-cip+A(1-xijp)≥tjp

(3)

cjp≥0;xijp,ajhp=0,1

(4)

cjp-cjh≥tjh

(5)

i,j=1,2,…,N;p,h=1,2,…,M

(6)

tjp：表示工件j在机器p上的加工时间；A表示一个值较大的正数；若工件i先于工件j在机器p上加工，则Xijp=1，否则Xijp=0；

当机器h比机器p先加工工件i时，aihp为1，否则aihp为0。

式(2)确保工序在某时刻只可在唯一机器上加工。

式(3)确保机器在某时刻仅加工唯一工件。

式(4)确保每道工序在此生产过程中都得到加工。

式(5)确保工件的加工顺序按给定的工艺路线进行。

同时，每个工件、同一工件的每道工序之间必须严格按照给定的工艺约束，工序开始加工之后不能中止，每个工件的优先级一样。

2 模拟退火算法的算法设计

模拟退火算法主要由升温过程、恒温过程和降温过程组成。升温过程是初始化温度参数的过程，一般选择一个较高温度作为初始温度，这样可以在一定程度上增加模拟退火算法搜索整个解空间最优解的机会，温度较高时，算法在进行Metropolis准则判断时可以选择较差的解作为个体解；当算法的温度变低时，算法收敛到最优解的概率逐渐变高。所以算法设计时一般选择较高的温度作为初始温度，用来增强算法跳出局部最优解的能力。降温过程一般用当前温度T乘以降温系数q来模拟降温过程，降温系数决定着退火速度。

模拟退火部分的主要步骤如下：

Step1:设定主要的控制参数。初始温度T0=1000C，降温速率q=0.2，结束温度Te=1e-3。

Step2:初始解。对于混合算法来说，初始解即是遗传算法中经过交叉、变异后的个体。

Step3:生产新解。新解在初始解的邻域生成。编程时通过随机选择相邻的两个工序，然后交换两者的加工顺序，产生新解。例如初始解S1=123214，新解可以是S2=213214，即交换了前两个工件的加工顺序。

Step4:Metropolis准则。用f(S1)表示初始解的适应度，f(S2)表示新解的适应度，那么df=f(S2)-f(S1),则Metropolis准则为：

(7)

3 混合调度算法的设计

分别对遗传算法和模拟退火算法的关键部分进行设计以后，得到的混合算法步骤如下：

Step1:设定混合算法的初始参数，包括种群的规模、遗传的代数、初始温度、降温系数、变异概率等参数；

Step2:依据个体的加工工艺进行染色体编码，采用工件工艺和机器的双层编码方式，同时随机初始化种群，并分析种群的适应度；

Step3:根据步骤step2的适应度进行个体选择操作，主要依据个体适应度的好坏来进行选择。适应度小的个体被选择遗传的概率也较小；

Step4:对选择的个体随机选择基因位置，进行交叉操作；

Step5:交叉完成后，根据变异率选择个体进行变异操作，产生新的个体，注意变异后要检查工艺的逻辑性；

Step6:对经过遗传操作后的种群，在染色体解的邻域内产生新的个体扰动解，并利用Metropolis准则判定是否接受新解；

Step7:执行参数的更新操作，如遗传代数，当前温度等；

Step8:如果相关参数没有达到规定的数值，则转到步骤Step3，当参数到达设定值之后，直接结束，输出最优解。

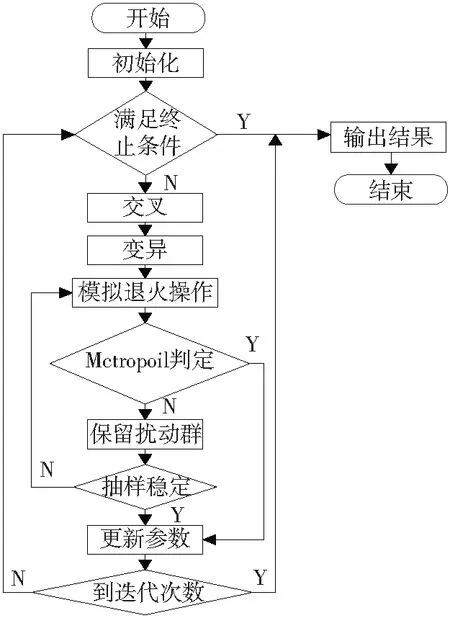
图1 混合算法流程图

4 算例分析

以FJSP生产系统为例。本算例以makespan最小为优化目标。对本文提出的改进前后的方法进行仿真并分析(软件版本为MATLAB2014a)。表1和表2给出了调度工艺及时间要求具。

表1 工件的工序逻辑表

表2 工件各工序的加工时间

表1给出的是6个工件的工艺加工要求，对每一个单独的工件来说，各个工序必须一次加工作业，工艺顺序不能颠倒。表中的2维数组是工件在加工相应工序时机器的可选集，因为在实际制造系统中，通常工件的某一道工序可以有多个机器满足加工条件，这样可以一定程度上避免因争抢机器资源而使制造系统陷入停顿。表2是按照表1 工序加工时对应所用的时间。

改进前：在单纯的遗传算法下，取初始参数个体数量为40，最大遗传代数为50，交叉率为0.8，变异率为0.1，得到甘特图如图2所示。

图2 遗传算法下的甘特图

图2显示了遗传算法产生的一组最优调度方案，所有工件按照调度方案加工完成所用的最短时间是52个时间单位；图3是遗传算法迭代过程中各代种群均值及最优解的变化情况，从图中可以看出，在经过10代之后，种群均值及最优解基本已经不再变化，但实际上是遗传算法陷入了过早熟现象的原因，遗传算法并没有搜索到真正有效的最优解。表3是遗传算法运行10次的得到的比较好的最优解情况。

图3 种群迭代次数

通过表3可以计算出遗传算法10次得到的调度最优解的均值为51.2个时间单位。

改进后：当采用混合算法时，同样采用表1和表2的工件工艺顺序和工艺时间，并取初始温度为1000℃，降温速率为0.2，得到的一组甘特图和种群均值图如图4和图5所示。

图4 混合算法下的甘特图

图5 种群均值及最优解变化

从图4 中可以看到，混合算法下按照调度方案完成所有工件加工的最优解时间是48个时间单位，从图5中可以看出混合算法使得种群的均值在15代以后才收敛到最小值，最优解也是如此。综上，从结果上可以看出混合算法由于模拟退火操作的加入，算法没有提前结束搜索使算法染色体想入同化的情况。表4是混合算法运行10次的结果。

表4 遗传算法运行10次的最优调度结果

通过表4可以得到混合算法在降温速率为0.2时，10次调度的平均时间是47.8个时间单位，调度方案的最优解要好于单纯的遗传算法。当降温速率变化时，通过实验得到的实验数据如表5所示。

表5 不同降温速度下混合算法及遗传算法最优解

从表5中可以看出，当遗传算法和混合算法对同一问题进行调度时，无论降温系数在0.1～0.9中间任何值，混合算法的调度最优解都要优于单纯的遗传算法所产生的调度方案。通过分析种群均值稳定的代数也可以发现，混合算法有效地解决了遗传算法所存在的过早熟现象，使得种群迭代过程中不再过度依赖于初始解的产生，同时，通过模拟退火操作，使得算法搜索整个解空间的能力大大加强，以降温速率为0.6的调度最优解为例，普通的遗传算法10次当中没有一次得到的最优解在50以下，而混合算法几乎有8次以上低于50，分析调度结果可知，调度最差的降温速率0.1也有6 次跳出了局部陷阱。而当降温速率为0.9时，混合算法几乎全部跳出了局部最优解，可见混合算法相对于单纯的遗传算法有着更好的跳出局部陷阱的能力，得到更优的调度方案。

5 结论

本文将遗传算法和模拟退火算法结合在一起，通过典型的柔性作业车间调度问题，将改进前后的调度结果进行比较分析，调度结果有了一定程度的提高，速度也有了一定程度的缩短，并将混合算法和单纯的遗传算法进行调度最优解的对比，详细的分析了两者收敛代数、调度时间，证明了混合算法的优于单纯的遗传算法，说明了这种混合算法在求解FJSP问题上的优势。

[1] 蓝萌, 徐汀荣, 黄斐. 使用混合邻域搜索算法求解多目标柔性JSP问题[J]. 计算机工程与设计, 2011, 32(1):293-296.

[2] 欧阳珍.基于遗传算法的车间调度研究与应用[D].杭州:浙江大学,2004.

[3] 柳青红,袁逸萍,李晓娟.基于改进遗传算法的作业车间调度[J].机械工程与自动化，2014(6):1-3.

[4] Zhang H P, Gen M. Multistage-based genetic algorithm for flexible job-shop scheduling problem[J].Journal Complexity, 2005, 11: 223-232.

[5] 陈振同,邢英杰.基于改进遗传算法的车间调度问题研究与应用[D]. 大连:大连理工大学，2007.

[6] 赵振勇,王力,王保华,等.遗传算法改进策略的研究[J].计算机应用,2006(S2):189-191.

[7] Mastrolilli M, Gambardella L M. Effective neighbourhood functions for the flexible job shop problem[J],Journal of Scheduling, 2000, 3 (1):3-20.

[8] KACEM I，HAMMADI S, BORNE P. Pareto-optimality approach for flexible job shop scheduling problems:hybridization of evolutionary algorithms and fuzzy logic[J].Mathematics and Computers in Simulation, 2002,60(3/4/5):245-276.

[9] 李运霞, 杜娟, 孙王路. 基于多种群遗传算法的路径柔性车间调度问题[J]. 组合机床与自动化加工技术, 2014(3):152-157.

[10] 刘韵, 胡毅, 罗企,等. 一种解决柔性车间作业调度问题的粒子群优化算法[J]. 组合机床与自动化加工技术, 2015(12):144-147.

[11]马磊磊, 王强. 基于改进遗传算法的多目标物料配送方法研究[J]. 组合机床与自动化加工技术, 2015(12):156-160.

(编辑 李秀敏)

Genetic Algorithm of Improved Initial Population Applying to Scheduling for Flexible Job Shop

NIU Lin

(College of Medical Information, Hainan Medical University, Haikou 571100,China)

The quality of the initial population of genetic algorithm have a decisive influence on the quality and speed. When traditional genetic algorithm is applied in solving flexible job shop scheduling problems, the initial population is randomly generated, which may result in forming many infeasible solutions at the beginning of the iteration. Only through a complex operation will form optimum solutions, it may greatly reduces convergence speed of the algorithm.After study the characteristics of flexible job shop scheduling,Initial population give rules of base on the entire Search to code and generate initial population′s strategy, has been put forward.When the quality of initial population be improved,its diversity also won′t lose. At the same time, its global convergence can be improved.The instance in this article using the improved genetic algorithm,the results are compared with the traditional genetic algorithm′s results, It proved that the advantages of improved algorithm.

genetic algorithm; flexible job shop scheduling; initial population

1001-2265(2017)08-0157-04

10.13462/j.cnki.mmtamt.2017.08.041

2016-09-10；

2016-10-21

牛琳(1978—)，女，黑龙江巴彦人，海南医学院讲师，硕士，研究方向为数据挖掘，信息管理，(E-mail)2763253868@qq.com.

TH186;TG659

A