异步伺服电机安装平台的模态与谐响应分析*

2017-09-08袁晓明

组合机床与自动化加工技术 2017年8期

袁晓明，高强

(1.燕山大学 a.河北省重型机械流体动力传输与控制重点实验室；b.先进锻压成形技术与科学教育部重点实验室，河北秦皇岛 066004；2.江苏徐州工程机械研究院，江苏徐州 221004)

袁晓明1a，1b，2，高强1a，1b

以某可靠性试验台用异步伺服电机安装平台为研究对象，拟对其动态特性开展研究。利用ANSYS软件建立安装平台结构有限元模型，对结构在不同预应力状态下的模态进行仿真，确定不同状态下结构的固有频率和振型，分析系统隔振效率随工作频率的变化规律，确定系统在常用工作频率下的隔振效率。基于谐响应仿真，研究电机底座上表面的位移、应力及应变分布，分析最大响应点随激励频率的变化规律，进而确定工装平台的振动敏感区域。上述研究为其它安装平台机械结构的动态优化设计奠定了理论基础。

异步伺服电机；安装平台；谐响应；隔振

0 引言

电机是一种将电能转换为机械能的能量转换装置，在工业设备中常用作驱动和加载单元，同时为设备的主要振动源。电机的安装平台主要起支撑电机和减振作用，其动力学性能直接影响与其相连的整个系统的动态特性，因此，研究电机安装平台的动态特性具有十分重要的意义。

国内外学者已对各种电机安装平台进行了研究，文献[1]利用有限元法对风力发电机机舱底座进行了模态与强迫振动响应分析，确定了底座应力与应变的敏感区域。文献[2]利用ANSYS对同步电动机底座进行了静力学和模态分析，分析了其变形特征和振型特点，为底座的轻量化设计提供了理论依据。文献[3]对带有隔振器的防爆柴油发电机组进行了振动分析，讨论了不同隔振器刚度对于系统隔振效果的影响规律。文献[4]利用Hyperworks以某型号电机底座的固有频率为目标进行了优化，提升了系统的1阶固有频率得，避免了共振。文献[5]通过谐响应分析确定了对结构影响最大的固有频率，并优化了结构的动态响应特性。

异步伺服电机的转速可调，适用性和应用均较广，但对其安装平台的动态特性研究较少，尤其在该类平台上的加速度传感器布置位置方面亟需进行深入探讨。拟以某企业可靠性试验台用异步伺服电机安装平台为研究对象，利用ANSYS软件通过模态分析和谐响应分析研究其动力学特性，从而为后续的结构优化和振动监测提供理论依据。

1 有限元仿真前处理

1.1 几何模型

设计了如图1所示的整体式结构异步伺服电机安装平台。该平台主要包括异步伺服电机，双膜片联轴器、过渡板、橡胶减振器和加强板等。过渡板和前面板，橡胶减振器与支撑块，电机和底座均通过螺栓连接。考虑到被试件和电机的安装有同轴度要求，在将前面板和后面板焊接后再进行镗孔，以保证同轴度误差在0.05mm以内。

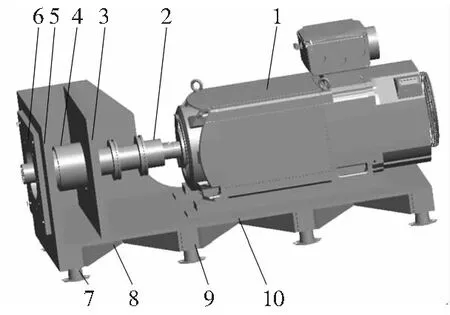
1.异步伺服电机 2.双膜片联轴器 3.后面板 4.轴承座 5.前面板 6.过渡板 7.橡胶减振器 8.加强板 9.支撑块 10.焊接底座
图1 安装平台的三维模型

异步伺服电机的振动直接影响其他关键元件和系统的性能，需对其进行隔振处理。橡胶减振器为主动隔振元件，因其阻尼大、刚度小及价格低等优点被广泛应用于各类行业。所选减振器为美国Korfund公司型号为RD3-Gray的橡胶减振器，主要由金属上骨架、橡胶体和金属下骨架组成，其剖面如图2所示。

1.金属上骨架 2.橡胶体 3.金属下骨架图2 橡胶减振器的剖面图

1.2 有限元模型

在有限元计算中，一般需将系统的结构进行简化，以减少网格数量和计算时间，但必须保证所建立的模型与实际模型具有较高的一致性。伺服电机的结构复杂，采用等质量的类圆柱体进行代替。将安装平台的几何模型离散化即可得到如图3所示的有限元模型。有限元模型中物理量信息的传递借助于网格节点，因此，网格划分质量对求解精度影响较大。若网格划分数量较多，则占用计算机内存大，求解速度过慢或问题无法求解；反之，求解速度快，但精度较低。由于各零部件尺寸间存在差异，采用“Body Sizing”网格划分命令，螺栓、减振器的几何尺寸较小，其网格尺寸设定为5mm；底座、过渡板等零件的几何尺寸较大，其网格尺寸设定为20mm。采用自动网格划分方法，根据几何体形状将各零部件划分为四面体或六面体网格。

图3 安装平台的有限元模型

1.3 螺栓预紧力

异步伺服电机的前面板与过渡板通过螺栓连接，但螺栓在长时间使用过程中存在松动、压溃失效和疲劳等问题，通过施加合适的预紧力可有效预防上述问题，一般螺栓的预紧力矩为：

Mt=0.001KtF0D

(1)

其中，Mt为螺栓预紧力矩(N·m)，Kt为预紧力系数，一般取为0.2，F0为螺栓预紧力(N)，D为螺栓直径(mm)。实际螺栓拧紧力矩值为135N·m，根据公式可确定螺栓预紧力为47kN。

1.4 材料参数与边界条件

为保证仿真模型的准确性，基于橡胶减振器的样本曲线和胡克定律确定其弹性模量。由材料力学单向拉伸实验结果可知，弹性模量的表达式为：

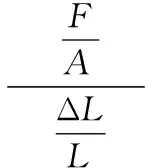
(2)

其中，E为弹性模量(MPa)；F为竖直方向的作用力(N)；A为横截面积(mm2)；ΔL为变形量(mm)；L为初始高度(mm)。

通过样本曲线拟合与公式(1)确定了RD3-Gray橡胶减振器的弹性模量为36MPa。拟通过仿真对橡胶减振器的弹性模量进行验证，利用Pro/E建立橡胶减振器的三维模型，在ANSYS中建立其有限元模型。依据单向拉伸实验的实际过程，设定底面为固定边界，顶面为轴向位移约束。橡胶减振器轴向位移云图如图4所示，橡胶减振器载荷位移曲线的仿真与样本对比结果如图5所示。

图4 橡胶减振器轴向变形云图

图5 橡胶减振器载荷位移曲线

由图4可知，橡胶减振器的底面为固定约束，因此其轴向位移为0；顶面为位移约束施加位置，因此其轴向位移的绝对值最大。由图5可知，仿真与样本的载荷位移曲线最大误差不超过1.5%，验证了所建立的减振器有限元模型的正确性。

在其它材料参数方面，橡胶减振器的密度为1200kg/m3；过渡板材料为20Cr合金板，密度为7800kg/m3，弹性模量为206GPa；螺栓材料为45号钢，密度为7800kg/m3，弹性模量为196GPa。

在边界条件方面，螺栓与过渡板，螺栓与底座等接触面采用“Frictional”摩擦接触，摩擦系数为0.2，其余接触面采用“Bonded”绑定接触。通过“Fixed Support”命令约束减振器底部所有自由度；通过“Bolt Pretension”命令分步设置过渡板与前面板间螺栓预紧力的施加和锁死，预紧力数值为47kN；通过“Moment”命令设置异步伺服电机的轴端输出扭矩，其方向遵循右手螺旋定则，大小为电机额定输出扭矩1500N·m。

2 动力学分析

2.1 模态分析

分别对安装平台的无预应力模态、螺栓预紧力作用下的预应力模态、螺栓预紧力和扭矩共同作用下预应力模态进行了仿真。无预应力模态的前6阶振型云图如图6所示，另两种预应力模态的振型结果与无预应力模态基本一致，在此不再一一列出。由模态分析确定的安装平台固有频率和振型如表1所示。

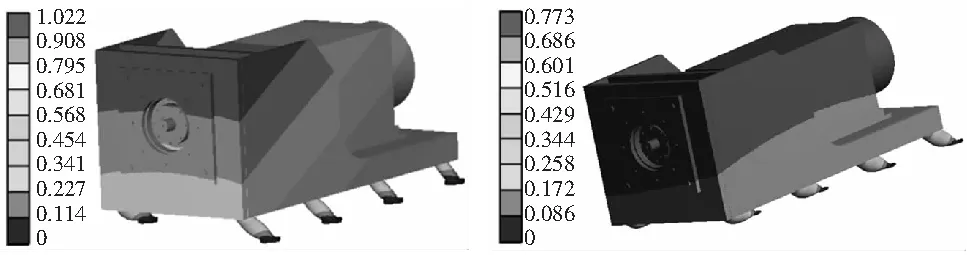
(a) 1阶模态 (b) 2阶模态

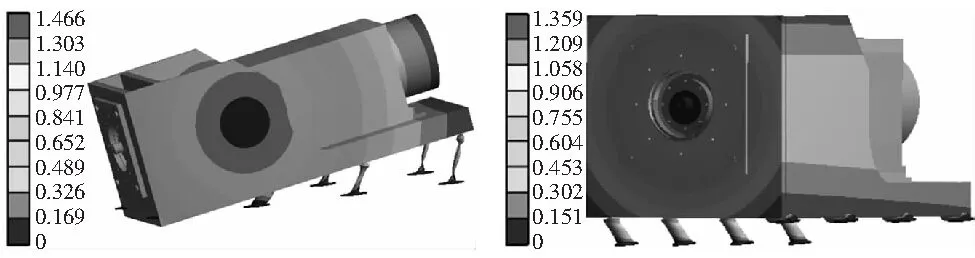
(e) 5阶模态 (f) 6阶模态图6 安装平台的前6阶模态振型云图

表1 安装平台固有频率及振型

由图6可知，异步电机安装平台低阶模态振型的主要变形区域分布在电机底座的前侧两端和后侧两端区域，上述位置为后续谐响应分析的重点研究区域。

由表1中数据可知，螺栓预紧力作用下的固有频率与无预应力下的固有频率基本一致，主要是由于螺栓尺寸与整体结构尺寸相比较小，螺栓预紧力仅增加了该位置的局部刚度，而对整体结构的模态影响不大；螺栓预紧力和扭矩共同作用下的固有频率明显增大，主要是由于电机实际工作过程中的扭矩作用提高了安装平台的整体刚度，从而对安装平台的整体模态产生了较大影响。异步伺服电机常用工作转速为1800～4000r/min，对应频率为30～67Hz，高于第6阶轴向扭转频率，但电机启动过程中必然经过这些固有频率，可能会引起振动，应在变频器中设置跳频点，避免电机启动和制动等过程中发生共振。

安装平台中配置了橡胶减振器，属于粘性阻尼系统，其振动传递率和隔振效率如式(3)和式(4)所示。

(3)

(4)

其中，a为橡胶减振器阻尼，取0.1；f0为异步伺服电机系统的固有频率，一般随着固有频率的增大，隔振效率有减低的趋势，故取螺栓预紧力和扭矩共同作用下的第6阶固有频率16.91Hz进行研究；f为异步伺服电机系统激励频率，取30～67Hz；T为振动传递率；ζ为隔振效率。通过计算确定了如图7和图8所示的系统振动传递率和系统隔振效率曲线，由图可知，随着激励频率的增加，振动传递率逐渐减小，隔振效率逐渐提高。在可靠性试验台工作时，伺服电机的常用频率为30Hz和67Hz时，当激励频率为30Hz时，隔振效率为52%，当激励频率为67Hz时，隔振效率达到90%。

图7 系统振动传递率曲线

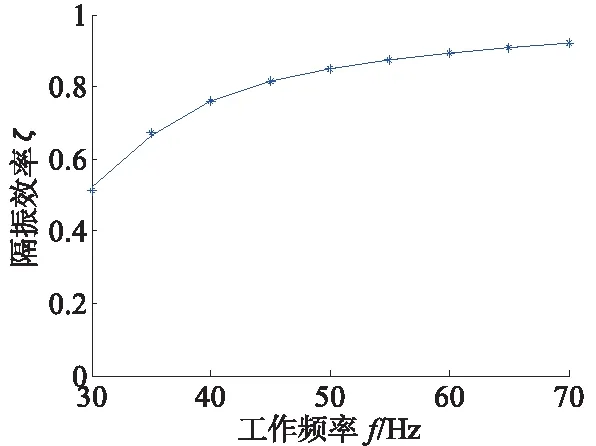
图8 系统隔振效率曲线

2.2 谐响应分析

异步伺服电机工作时，许多实际工况要求其以正弦波的形式输出转矩，因此必须分析安装平台在工作频率下的谐响应。取常用的激振力矩1500N·m，观测频率范围为3～75Hz。以电机底座的上表面为主要分析对象，该表面的位移、应力及应变如图9所示。

(a) 位移云图

(b) 应力云图

由图9可知，位移最大响应主要位于底座前侧两端区域，应力和应变最大响应主要位于底座后侧两端区域。以最大响应点作为分析对象，分别得到对应点的幅频特性曲线，如图10所示。

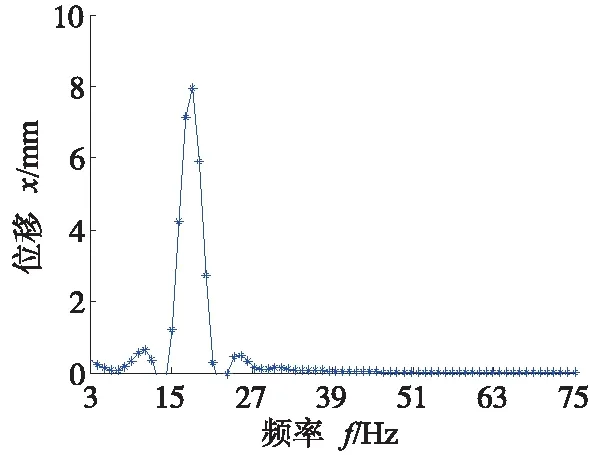
(a) 位移最大响应点

(b) 应力最大响应点

由图10可知，随着激励频率增加，底座的位移、应力及应变也随之发生变化，且在激励频率为17.5Hz左右时，三者同时达到了峰值，位移、应力及应变的振动幅值分别为8.051mm、4.235MPa及0.000045。仿真确定的峰值频率对应于模态分析中的第6阶X向扭转固有频率。当激励频率在18Hz以上时，由于避开了系统的固有频率，振动幅值随着频率的增加快速下降，当激励频率达到40Hz上时，振动幅值均逐渐趋于0。因此，电机底座上表面两端区域为比较合理的加速度传感器安装位置。

3 结论

(1) 建立了异步伺服电机安装平台的几何模型和有限元模型。

(2) 通过不同预应力状态下模态分析可知，局部螺栓预紧力对整体结构的固有频率影响不大，扭矩载荷能够提高整体结构刚度，增加系统的固有频率。基于数学方法计算了异步伺服电机安装平台的隔振效率，该隔振效率随激励频率的增加而增加，当激励频率为30Hz时，隔振效率为52%，当激励频率为67Hz时，隔振效率达到90%。

(3) 基于谐响应分析确定了异步伺服电机安装平台的振动敏感区域主要位于电机底座上表面两端区域，该区域为比较合理的加速度传感器安装位置。最大响应点的峰值频率在17.5Hz左右，对应于模态分析中的第6阶X向扭转固有频率。位移、应力及应变的振动幅值分别达到了8.051mm、4.235MPa及0.000045。

[1] 龚宇琴, 苗风麟, 施洪生. 风力发电机机舱底座模态及动态载荷分析[J]. 可再生能源, 2014, 32(1):49-53.

[2] 范进桢, 白双建, 姚振强,等. TAW型同步电动机底座的有限元分析[J]. 机械设计, 2011, 28(2):23-25.

[3] 赵禹. 某机车用柴油发电机组的隔振设计及优化[J]. 机械工程与自动化, 2014(6):59-61.

[4] 吴学锋, 张保成, 刘宇航. 某型号电机底座模态分析及固有频率的优化[J]. 机械研究与应用, 2014(1):57-59.

[5] Bhaskararao A V, Jangid R S. Harmonic response of adjacent structures connected with a friction damper [J]. Journal of Sound & Vibration, 2006, 292(3-5):710-725.

[6] 刘成颖, 谭锋, 王立平,等. 面向机床整机动态性能的立柱结构优化设计研究[J]. 机械工程学报, 2016, 52(3):161-168.

[7] 杨玉萍, 张森, 季彬彬,等. 立式加工中心床身结构动态特性有限元分析[J]. 机械设计与制造, 2014(1):174-176.

[8] 黄冠华, 王兴宇, 梅桂明, 等. 内外激励下高速列车齿轮箱箱体动态响应分析[J]. 机械工程学报, 2015, 51(12):95-100.

[9] 权凌霄, 骆洪亮, 张晋,等. 斜轴式轴向柱塞泵壳体结构振动谐响应分析[J]. 液压与气动, 2014(5):33-39.

[10]季彬彬, 张森, 杨玉萍,等. GMF3022龙门加工中心横梁的模态及谐响应分析[J]. 组合机床与自动化加工技术, 2013(10):36-38.

(编辑李秀敏)

Modal and Harmonic Response Analysis of Asynchronous Servo Motor Installation Platform

YUAN Xiao-ming1a,1b,2, GAO Qiang1a,1b

(1 a.Hebei Key Laboratory of Heavy Machinery Fluid Power Transmission and Control;b. Key Laboratory of Advanced Forging & Stamping Technology and Science, Ministry of Education of China, Yanshan University, Qinhuangdao Hebei 066004,China;2. Jiangsu Xuzhou Construction Machinery Research Institute, Xuzhou Jiangsu 221004,China)

Taking the asynchronous servo motor installation platform for reliability test bench as the research object, its dynamic characteristics are studied. Finite element model of installation platform structure is established by software ANSYS. Different pre-stress modal simulation of the structure are carried out, and nature frequencies and modal shapes are determined under different situations. Change rules between the vibration isolation efficiency of system with working frequency are analyzed, and vibration isolation efficiency of system under normal working frequency is determined. Distribution of displacement, stress and strain are studied based on harmonic response analysis. Change rules between the maximum response points with excitation frequency are analyzed, and vibration sensitive areas of installation platform are found. The studies lay a theoretical foundation for the dynamic optimal design of other installation platform mechanical structures.

asynchronous servo motor; installation platform; harmonic response; vibration isolation

1001-2265(2017)08-0040-04

10.13462/j.cnki.mmtamt.2017.08.010

2017-04-19

河北省自然科学基金青年科学基金(E2017203129)；燕山大学基础研究专项课题青年课题(16LGB001)

袁晓明(1984—)，男，吉林白城人，燕山大学讲师，博士，研究方向为流体传动与控制、机械结构优化设计，(E-mail)yuanxiaoming@sdu.edu.cn。

TH122；TG659