一类线性侧位系统的极限环分支
2017-09-07于江赵倩倩
于江,赵倩倩
(上海交通大学 数学科学学院,上海 200240)
一类线性侧位系统的极限环分支
于江,赵倩倩
(上海交通大学 数学科学学院,上海 200240)
讨论了一类焦点-焦点型线性侧位系统(即夹角为θ∈(0,π)的两扇形区域不连续线性动力系统)极限环分支,证明了此类系统极限环的环性为2,并给出分支图。且可扰动系统参数,使得线性侧位系统存在3个极限环。
不连续分段动力系统;线性侧位系统;焦点-焦点型;极限环分支
1 研究背景和主要结论
不连续动力系统在电子、力学、经济学等方面有着广泛的应用。近年来, 不连续动力系统的研究发展迅速,特别是侧位系统引起人们的关注。为了更方便地描述问题,我们给出如下定义:
定义1.1 系统
(1.1)
称为侧位系统,其中Σ+和Σ-是由有相同起点且夹角θ∈(0,π)的两条射线将2分成的两个扇区。当子系统X+(x,y)和X-(x,y)都为线性系统时,我们称此系统为线性侧位系统。
显然,当θ=π时, (1.1) 为分段线为一条直线的平面分段线性系统;当θ=0时, (1.1)为连续平面线性系统。很自然地,我们会考虑问题:若分段射线的夹角θ从0到π变化时,线性分段系统的极限环个数有什么变化。
有关θ=π时(即分段线为一条直线的平面不连续线性动力系统)的研究结果已经很丰富(参见文献[1]-[11])。Llibre等在文献[8]中按两子系统的类型总结了各类平面分段线性系统的极限环个数的下界(见表1),其中焦点型包括焦点和中心。关于分段系统极限环个数上界(环性)的研究结论较少,Llibre等在文献[13]和文献[14]中得到了有一个奇点在分段线上的分段线性动力系统的极限环上界是2。但一般分段线性系统的环性(上界)仍然是公开问题。

表1 θ=π时系统(1.1)极限环个数的下界
关于线性侧位系统,Llibre*Llibre J,Medrado J,Ramírez O.Limit Cycles of Planar Discontinuous Piecewise Linear Differential Systems Defined in Two Sections,Preprint.得到了一个子系统的奇点在原点的线性侧位系统的极限环个数上界为2,Cardin和Torregrosa用高阶Melnikov函数得到了角度为π/2的线性侧位系统存在5个极限环(见文献[12])。
从目前的研究结果来看, 线性侧位系统的极限环数目比θ=π时线性系统(1.1)极限环数目大。其原因何在?我们发现当θ=π时, 焦点型线性子系统的庞卡莱映射的图像为严格单调下降且无拐点的曲线或为严格单调下降的射线(参见文献[9])。而对于线性侧位系统,即0<θ<π时, 我们*Q Zhao,J Yu.Limit cycles of a class of discontinuous planar piecewise linear systems with three regions of Y-type, preprint.证明焦点型线性子系统的庞卡莱映射的图像为严格单调下降且至多有一个拐点的曲线或为严格单调下降且无拐点的曲线或为严格单调下降的射线。由此我们可以看出, 对于某一子系统为焦点型的分段线性系统而言, 分段线夹角的改变会使得子系统的庞卡莱映射的图像性质发生变化, 从而使系统的极限环个数发生变化。也可看出,夹角θ=0和θ=π为临界值(随后我们会得出非退化线性变换(1.2)可将夹角为0<θ<π的线性侧位系统化为夹角为π/2的线性侧位系统)。本论文将给出一类焦点-焦点型线性侧位系统的极限环分支, 得到了此类系统可存在0, 1和2个且最多存在2个极限环的结论, 并分情况给出分支图。与分段线为直线的情形相比较, 焦点-焦点型线性系统在相同条件下,存在且最多存在一个极限环 (参见文献[9])。
我们给出有关线性侧位系统的一些定义和本论文的主要结论:
不失一般性, 在线性侧位系统中, 我们假设两条起点相同的射线分别为
Γ1:x=0, 其中y≥0,
Γ2:y=kx, 其中x≤0,
且Σ-为θ∈(0,π)所对应的扇区, 如图1(a)所示。作如下线性变换

(1.2)

(1.3)
其中X=(x,y)T∈2,A=(aij)和C=(cij)为2×2的常数矩阵,h=(h1,h2)T和r=(r1,r2)T是2中的常向量,Σ+和Σ-是由y轴的正半轴和x轴的负半轴所分成的两个扇区且Σ-是夹角π/2所对应的扇区。我们分别用(x+,y+)和(x-,y-)表示系统H+(X)和H-(X)的奇点。

Fig.1 Illustration of lateral systems图1 线性侧位系统的分块

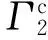

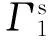

(1.4)
系统(1.3)含有12个参数,故将(1.3)的极限环分支讨论清楚非常困难。在本文中, 我们考虑在下列假设条件下系统(1.3)的极限环分支:
假设(H1):线性系统H+(X)和H-(X)均为焦点型;
假设(H2):系统H+(X)的焦点在原点. 系统(1.3)无滑动区间.
本文主要结论如下:
定理1.1 在假设条件(H1)和(H2)下, 系统(1.3)最多存在2个极限环, 且可以找到合适的参数使得系统(1.3)有0个, 1个或2个极限环, 并给出参数分支图(见图3-7)。
定理1.2 在假设条件(H1)下, 当‖r‖≪1时, 系统(1.3)存在3个极限环。
2 子系统庞卡莱映射的性质
在本节中,我们分别给出系统(1.3)在假设(H1)和(H2)下的标准型及所满足的条件, 以及两个子系统的庞卡莱映射的性质.
由Theorem 1.1*Llibre J,Medrado J,Ramírez O.Limit Cycles of Planar Discontinuous Piecewise Linear Differential Systems Defined in Two Sections,Preprint.可知, 在假设(H1)和(H2)下线性侧位系统(1.3)的标准型为
(2.1)
其中γ-,γ+,h1,h2,u,v和β均为中的参数,其中β>0。
在假设(H2)下, 由式(1.4)可知系统(2.1)应满足下列条件:
h1≤0,h2≤0.
(2.2)
故本文我们将在条件(2.2)下考虑系统(2.1)极限环分支。
为方便起见, 在以后的讨论中, 若没有特别说明, 均假设条件(H1)和(H2)成立。我们仍然用H+和H-分别表示在Σ+和Σ-上的子系统。
系统H+的起点为(x1,0)的轨线, 其中x1<0在x轴负半轴的流的作用下从点(x1,0)进入扇区Σ+, 再在Σ+的流的作用下到达y轴的正半轴上的点(0,y1)。故我们可以定义系统H+的庞卡莱映射P+为y1=P+(x1), 其中P+(0)=0(参看图2)。

Fig.2 Illustration of Poincaré maps y1=P+(x1) and x1=P-(y0)图2 庞卡莱映射y1=P+(x1)和x1=P-(y0)的示意图
命题2.1 (系统H+的庞卡莱映射的性质) 系统H+的庞卡莱映射为起点在原点且斜率k+∈(-,0)的射线, 其形式为
(2.3)
其中,

证明 系统H+的通解为
其中
类似定理1.2(c)*Llibre J,Medrado J,Ramírez O.Limit Cycles of Planar Discontinuous Piecewise Linear Differential Systems Defined in Two Sections,Preprint.的证明及引理4.1①, 直接计算可得此命题。
系统H-的起点为(0,y0)的轨线, 其中y0>0, 在y轴正半轴的流的作用下从点(0,y0)进入扇区Σ-,再在Σ-的流的作用下到达x轴的负半轴上的点(x1,0)。故我们可以定义系统H-的庞卡莱映射P-为x1=P-(y0),其中P-(0)=0(参看图2)。□
命题2.2 (系统H-的庞卡莱映射的性质1)
(1)当h1=h2=0时,系统H-的庞卡莱映射为射线
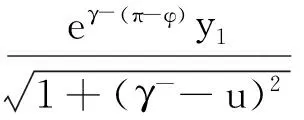
(2.4)
其中
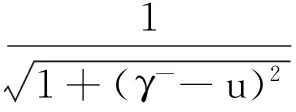

(2.5)
其中
Q(t-)=(y-)2-[1+(γ--u)2](x-)2e2γ-t--2γ-ψ(γ--u)(t-)x-y-eγ-t-,
ψα(t)=cost-αsint.
证明 系统H-的通解为
其中
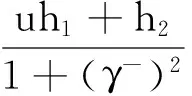
(1)类似命题2.1, 计算可得。

(2.6)
φγ(t)=1-eγt(cost-γsint),

求导计算易得(2.5)成立。于是, 类似定理1.2(b)*Llibre J,Medrado J,Ramírez O.Limit Cycles of Planar Discontinuous Piecewise Linear Differential Systems Defined in Two Sections,Preprint.的证明, 由Q′(t-)≠0可得Q(t-)单调,因此P″-(y0)至多一个零点。可知(2)成立。□
明显地,在条件(2.2)下,系统H-的参数(h1,h2,γ-,u)∈A, 其中
A={(h1,h2,γ-,u)∣h1≤0,h2≤0}.
令A=A1∪A2∪…∪A6,其中
A1={(h1,h2,γ-,u)∣h1=0,h2=0},
A2={(h1,h2,γ-,u)∣h1≤0,h2≤0,γ-x-=0,Q(0)=0}A1,
A3=A31∪A32∪A33,
A4=A41∪A42∪A43,
A5={(h1,h2,γ-,u)∣h1≤0,h2≤0,γ-x->0,Q(0)>0,Q(π-φ)<0}A1,
A6={(h1,h2,γ-,u)∣h1≤0,h2≤0,γ-x-<0,Q(0)<0,Q(π-φ)>0}A1,
且
A31={(h1,h2,γ-,u)∣h1≤0,h2≤0,γ-x->0,Q(0)≤0}A1,
A32={(h1,h2,γ-,u)∣h1≤0,h2≤0,γ-x-<0,Q(0)<0,Q(π-φ)≤0}A1,
A33={(h1,h2,γ-,u)∣h1≤0,h2≤0,γ-x-=0,Q(0)<0}A1,
A41={(h1,h2,γ-,u)∣h1≤0,h2≤0,γ-x-<0,Q(0)≥0}A1,
A42={(h1,h2,γ-,u)∣h1≤0,h2≤0,γ-x->0,Q(0)>0,Q(π-φ)≥0}A1,
A43={(h1,h2,γ-,u)∣h1≤0,h2≤0,γ-x-=0,Q(0)>0}A1.
显然,Ai∩Aj=∅,i≠j.
命题2.3 (系统H-的庞卡莱映射的性质2) 若(h1,h2,γ-,u)∈A, 则系统H-的庞卡莱映射
x1=P-(y0)∶[0,+)→(-,0],其中P-(0)=0,
且有
(a)当(h1,h2,γ-,u)∈A1∪A2时,x1=P-(y0)为单调下降的射线;
(b)当(h1,h2,γ-,u)∈A3时,x1=P-(y0)为单调下降全局凸的曲线;
(c)当(h1,h2,γ-,u)∈A4时,x1=P-(y0)为单调下降全局凹的曲线;
(d)当(h1,h2,γ-,u)∈A5时,x1=P-(y0)为单调下降先凹后凸的曲线;
(e)当(h1,h2,γ-,u)∈A6时,x1=P-(y0)为单调下降先凸后凹的曲线。
注:此处凹凸指的是下凹和上凸。
证明 显然
x1=P-(y0):[0,+)→(-,0], 其中P-(0)=0,
由于(a)-(e)的证明比较类似, 我们仅给出五个中较为复杂的(d)的证明, 其余四个完全类似。
当(h1,h2,γ-,u)∈A5时, 我们有γ-x->0,Q(0)>0和Q(π-φ)<0。由式(2.5), 可得
sign(Q′(t-))=-sign(γ-x-)=-1,
故Q(t-)为单调递减的函数, 又由于Q(0)>0且Q(π-φ)<0, 故存在t0∈(0,π-φ)使得Q(t0)=0且
Q(t)>0,t∈(0,t0),
Q(t)<0,t∈(t0,π-φ).
又由式(2.5),有
sign(P″-(y0))=sign(Q(t-)),
故
P″-(y0)>0,t∈(0,t0),
P″-(y0)<0,t∈(t0,π-φ),
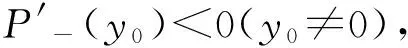
3 定理1.1的证明
在本节中, 我们首先分别讨论在条件(2.2)下系统H-的参数分别属于Ai(i=1,2,…,6)时,系统(2.1)的极限环分支,再在此基础上证明定理1.1。
为了寻找系统(2.1)的极限环,我们定义系统(2.1)的庞卡莱映射为其两个子系统的复合, 即
y1=P(y0)∶=P+∘P-(y0),
(3.1)
我们将P0定义为系统(2.1)的庞卡莱映射在0点的导数,P定义为其在无穷远处的极限值, 即
P0∶=P′(0)
(3.2)
P).
(3.3)
我们后面将以P0和P作为分支参数给出分支图。
命题3.1 (系统(2.1) 的庞卡莱映射的性质) 若(h1,h2,γ-,u)∈A, 则系统(2.1)的庞卡莱映射
y1=P(y0)∶[0,+)→(-,0], 其中P(0)=0,
且有
(a)当(h1,h2,γ-,u)∈A1∪A2时,y1=P(y0)为单调上升的射线;
(b)当(h1,h2,γ-,u)∈A3时,y1=P(y0)为单调上升全局凹的曲线;
(c)当(h1,h2,γ-,u)∈A4时,y1=P(y0)为单调上升全局凸的曲线;
(d)当(h1,h2,γ-,u)∈A5时,y1=P(y0)为单调上升先凸后凹的曲线;
(e)当(h1,h2,γ-,u)∈A6时,y1=P(y0)为单调上升先凹后凸的曲线。
证明 系统(2.1) 的庞卡莱映射为其两个子系统的复合, 由命题2.1, 命题2.3和式(3.1)可得

故此命题成立。□
命题3.2 在条件(2.2)下系统(2.1)的庞卡莱映射有如下性质
(a)若(h1,h2,γ-,u)∈A, 则
P=k>0,
其中
且y1=P(y0)的渐近线为
y1=Py0+B,
其中

(b)若(h1,h2,γ-,u)∈A,则

若(h1,h2,γ-,u)∈A2∪A3∪…∪A0。 则
证明 由式(2.3),(2.4)和(2.6)及(3.1),(3.2)和(3.3)容易得到此命题成立。□
寻找系统(2.1)在条件(2.2)下的极限环等价于寻找方程P(y0)=y0的正解, 亦等价于寻找方程P-(y0)=(P+)-1(y0)的正解. 定理3.1-3.5给出了参数属于不同范围时极限环的分支图, 其中需要注意的是定理中参数范围不同时P0的值取不同(P0的取值见命题3.2)。我们仅证明定理3.1-3.5中较复杂的3.5, 其他四个定理的证明非常类似。
注:由于P0≥0和P∞>0,故在下面定理3.1-定理3.5中分别以P0和P∞为横坐标的分支图都定义在第一象限y轴正半轴上(不包含原点和x轴正半轴)。
定理3.1 在条件(2.2)下,参数属于A1∪A2时, 系统(2.1)有分支图3,且
(a) 当P0=1时, 系统(2.1)的原点为全局中心;
(b)当P0≠1时, 系统(2.1)无极限环。

Fig.3 Bifurcation of limit cycles when (h1,h2,γ-,u)∈A1∪A2图3 (h1,h2,γ-,u)∈A1∪A2时的极限环分支图
定理3.2 在条件(2.2)下,参数属于A4时, 系统(2.1)有分支图4,且
(a) 当P0≤1或P0>1且P≥1时, 系统(2.1)无极限环;

Fig.4 Bifurcation of limit cycles when (h1,h2,γ-,u)∈A3图4 (h1,h2,γ-,u)∈A3时的极限环分支图
(b) 当P0>1且P<1时, 系统(2.1)有唯一极限环。
定理3.3 在条件(2.2)下, 参数属于A3时, 系统(2.1)有分支图5, 且
(a) 当P0≥1或P0<1且P≤1时, 系统(2.1)无极限环;
(b) 当P0<1且P>1时, 系统(2.1)有唯一极限环。

Fig.5 Bifurcation of limit cycles when (h1,h2,γ-,u)∈A4图5 (h1,h2,γ-,u)∈A4时的极限环分支图
定理3.4 在条件(2.2)下, 参数属于A5时, 系统(2.1)有分支图6,且
(a) 当P0≤1且P≤1时, 系统(2.1)无极限环;
(b) 当P0≤1且P>1或P0>1且P<1时, 系统(2.1)有唯一极限环;
(c) 当P0>1, P=1时, 如果B≥0, 系统(2.1) 不存在极限环, 如果B<0, 系统(2.1) 存在1个极限环;
(d) 当P0>1且P>1时, 系统(2.1)存在0, 1或2个极限环。

Fig.6 Bifurcation of limit cycles when (h1,h2,γ-,u)∈A6图6 (h1,h2,γ-,u)∈A6时的极限环分支图
定理3.5 在条件(2.2)下, 参数属于A6时, 系统(2.1)有分支见图7,且
(a) 当P0≥1且P≥1时, 系统(2.1)无极限环;
(b) 当P0≥1且P<1或P0<1且P>1时, 系统(2.1)有唯一极限环;
(c) 当P0<1, P=1时, 如果B≤0, 系统(2.1) 不存在极限环, 如果B>0, 系统(2.1) 存在1个极限环(此处, 我们仅用一维线段来表示B, P0两参数集合);
(d) 当P0<1且P<1时, 系统(2.1)存在0, 1或2个极限环。

Fig.7 Bifurcation of limit cycles when (h1,h2,γ-,u)∈A5图7 (h1,h2,γ-,u)∈A5时的极限环分支图
证明 在条件(2.2)下且系统H-的参数属于A6时, 由命题3.1知系统(2.1)的庞卡莱映射的图像为起点为原点且单调上升先凹后凸的曲线 。
(a) 当P0≥1且P≥1时, 由系统(2.1)的庞卡莱映射图像的单调性和凹凸性知其图像在射线y1=y0(y0≥0)的上方, 两个函数图像除了原点外无交点, 故系统(2.1) 不存在极限环, 参见图8(a)。
(b) 当P0≥1且P<1或P0<1且P>1时, 由系统(2.1)的庞卡莱映射图像的单调性和凹凸性知其图像与射线y1=y0(y0≥0)除了原点外仅有一个交点, 故系统(2.1)有唯一极限环, 参见图8(a)和8(c)。
(c) 当P0<1, P=1时, 若B≤0, 则系统(2.1) 的庞卡莱映射的图像在射线y1=y0(y0≥0)的下方, 两图像无除了原点以外的交点, 故系统(2.1) 不存在极限环, 若B>0, 则系统(2.1) 的庞卡莱映射的图像当y0→0时在射线y1=y0(y0≥0)的下方, 当y0→+在射线y1=y0(y0≥0)的上方。由系统(2.1)的庞卡莱映射图像的单调性和凹凸性知其图像与射线y1=y0(y0≥0)除了原点外仅有一个交点, 故系统(2.1)存在唯一的极限环, 参见图8(d)。
Fig.8 Illustration of y1=P(y0) when (h1,h2,γ-,u)∈A5图8 (h1,h2,γ-,u)∈A5时y1=P(y0)图像示意图
(d) 当P0<1且P<1时,若系统(2.1)的庞卡莱映射的图像在射线y1=y0(y0≥0)的下方,两个函数图像除了原点以外的无交点,故系统(2.1)不存在极限环。若系统(2.1)的庞卡莱映射的图像与射线y1=y0(y0≥0)相切,则由其单调性和凹凸性知两个图像除了原点之外仅有一个交点,即切点(L1即为切点参数曲线),故系统(2.1)存在1个极限环。若系统(2.1)的庞卡莱映射的图像有一部分在射线y1=y0(y0≥0)的上方, 则由其单调性和凹凸性知两个函数的图像除了原点之外有两个交点, 故系统(2.1)存在2个极限环, 参见图8(b)。
两个极限环是可以实现的。例如:在(c)中, 当P0<1,P=1且B>0时,系统(2.1)有唯一极限环,我们通过扰动参数使得0<1-P≪1时,此时系统(2.1)存在两个极限环。□
定理1.1的证明 由定理3.1-定理3.5可直接得到定理1.1。□
4 定理1.2的证明
在H1条件下, 不妨考虑标准形(2.1)的参数扰动系统如下
(4.1)
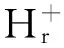
P=P+∘P-∶(0,+)).

Fig.9 Illustration of Poincaré map of when |r1|≪1图9 当|r1|≪1时的庞卡莱映射示意图

Fig.10 Graph of Poincaré map y1=P(y0) when |r1|≪1图10 当|r1|≪1时庞卡莱映射y1=P(y0)的图像
[1]LumR,ChuaL.GlobalPropertiesofContinuousPiecewise-linearVectorFields,PartI:SimplestCasein2[J].International Journal of Circuit Theory and Applications,1991,19(3):251-307:DOI:10.1002/cta.4490190305.
[2]LlibreJ,OrdóezM,PonceE.OntheExistenceandUniquenessofLimitCyclesinaPlanarPiecewiseLinearSystemsWithoutSymmetry[J].Nonlinear Analysis Series B:Real World Applications,2013,14(5):2002-2012.DOI:10.1016/j.nonrwa.2013.02.004.
[3]FreireE,PonceE,RodrigoF,et al.BifurcationSetsofContinuousPiecewiseLinearSystemswithTwoZones[J].International Journal of Bifurcation and Chaos,1998,8(11):2073-2097.DOI:10.1142/S0218127498001728.
[4]HanM,ZhangW.OnHopfbifurcationinNon-smoothPlanarSystems[J].Journal of Differential Equations,2010,248(9):2399-2416.DOI:10.1016/j.jde.2009.10.002.
[5]HuanS,YangX.TheNumberofLimitCyclesinGeneralPlanarPiecewiseLinearSystems[J].Discrete and Continuous Dynamical Systems,2012,32(6):2147-2164.DOI:10.3934/dcds.2012.32.2147.
[6]HuanS,YangX.OntheNumberofLimitCyclesinGeneralPlanarPiecewiseLinearSystemsofNode-nodeTypes[J].Journal of Mathematical Analysis and Applications,2014,411(1):340-353.DOI:10.1016/j.jmaa.2013.08.064.
[7]HuanS,YangX.ExistenceofLimitCyclesinGeneralPlanarPiecewiseLinearSystemsofSaddle-saddleDynamics[J].Nonlinear Analysis:Theory,Methods & Applications,2013,92:82-95.DOI:10.1016/j.na.2013.06.017.
[8]LlibreJ,PonceE.ThreeLimitCyclesInDiscontinuousPiecewiseLinearDifferentialSystemswithTwoZones[J].Dynamics of Continuous,Discrete and Impulsive Systems,2012,19:325-335.
[9]FreireE,PonceE,TorresF.CononicalDiscontinuousPlanarPiecewiseLinearSystems[J].SIAM Journal on Applied Dynamical Systems,2012,11(1):181-211.DOI:10.1137/11083928X.
[10]FreireE,PonceE,TorresF.TheDiscontinuousMatchingofTwoPlanarLinearFociCanHaveThreeNestedCrossingLimitCycles[J].Proceedings of New Trends in Dynamical Systems,2014:221-253.DOI:10.5565/PUBLMATExtra14 13.
[11]KuznetsovY,RinaldiS,GragnaniA.One-parameterBifurcationsinPlanarFilippovSystems[J].International Journal of Bifurcation and Chaos,2003,13(8):2157-2188.DOI:10.1142/S0218127403007874.
[12]CardinP,TorregrosaJ.LimitCyclesinPlanarPiecewiseLinearDifferentialSystemsWithNonregularSeparationLine[J].Physica D:Nonlinear Phenomena,2016,337:67-82.DOI:10.1016/j.physd.2016.07.008.
[13]LlibreJ,NovaesD,TeixeiraM.LimitCyclesBifurcatingfromthePeriodicOrbitsofaDiscontinuousPiecewiseLinearDifferentiableCenterwithTwoZones[J].International Journal of Bifurcation and Chaos,2015,25(11):1550144.DOI:10.1142/S0218127415501448.
[14]LlibreJ,NovaesD,TeixeiraM.MaximumNumberofLimitCyclesforCertainPiecewiseLinearDynamicalSystems[J].Nonlinear Dynamics,2015,82(3):1159-1175.
The Bifurcation of Limit Cycles of a Class of Lateral Systems
YU Jiang,ZHAO Qianqian
(School of Mathematical Sciences,Shanghai Jiaotong University,Shanghai 200240,China)
A class of linear lateral systems with focus-focus type is considered, that is, the discontinuous piecewise linear systems with two zones of the angleθ∈(0,π). It is provided the bifurcation diagram, which shows that there exist 0, 1 and 2 limit cycles in such systems, respectively. And the lateral systems can have 3 limit cycles by perturbing some parameters.
discontinuous piecewise dynamical systems;linear lateral systems;focus-focus type;limit cycles
10.13451/j.cnki.shanxi.univ(nat.sci.).2017.03.001
2017-05-15;
2017-06-30
国家自然科学基金(11431008;11501193);上海自然科学基金(15ZR1423700)
于江(1967-),博士,教授。E-mail:jiangyu@sjtu.edu.cn
O19
A
0253-2395(2017)03-0395-11
