相关变量随机数序列产生方法∗

1 引言

蒙特卡罗方法在很多领域得到了广泛的应用[1−7].由具有已知分布的随机变量进行抽样的方法在蒙特卡罗方法中占有重要的地位,并且已得到广泛的研究.对于多维随机变量的蒙特卡罗模拟问题,通常假定各随机变量之间是相互独立的,由此可以根据每个变量的统计分布去独立产生多变量的样本.但在某些学科,比如核工程中的不确定性分析,不仅同一反应类型每个能群与每个能群的多群截面是相关的,不同反应类型同一反应能群的截面也是相关的,故需要对多维具有相关性的随机变量进行模拟.这就需要产生具有相关系数矩阵的多个随机数序列.之前的研究表明,基于协方差矩阵的Cholesky因子分解的线性变换方法被认为是最好的一种方法[8],但Cholesky因子分解的线性变换方法要求协方差矩阵必须是正定的,而对于很多实际问题的协方差矩阵,正定条件并不一定能完全满足,这时如果还采用Cholesky因子分解并做近似处理可能出现较大误差.针对这样的问题,本文提出了基于Jacobi矩阵分解法进行相关随机变量序列产生的方法,相比于Cholesky因子分解,Jacobi矩阵分解法不要求矩阵正定,只要满足对称即可,这样就进一步扩展了相关随机变量序列的产生方法.并且进一步发现,如果协方差矩阵本征值部分为负值时,采用不同的置零修正方法,误差有较大差别.

2 相关随机变量模拟理论

由于正态分布具有在线性变换下保持分布规律不变的独特性质,因此多维相关正态分布随机变量抽样序列可以通过方差矩阵进行分解,然后对独立正态分布抽样序列进行线性变换来产生[8].之前研究较多的是采用Cholesky分解,下面证明:不仅可以采用Cholesky分解,其他的分解方式只要能满足把协方差矩阵A分解成矩阵Σ和ΣT的相乘的形式,即

则就可以利用矩阵Σ产生多维相关正态分布随机变量.

设Xm×n=(X1,X2,...,Xn)m为需要产生的m组n维相关正态分布随机变量序列,其均值为u=(u1,u2,...,un),协方差矩阵为A,表示如下:

对于核工程中截面的不确定性分析,Ai,j为分群截面之间的协方差矩阵.产生n维独立标准正态分布随机变量抽样序列Ym×n=(Y1,Y2,...,Yn),每个变量抽样序列数m,并且Xn,Yn和Σ满足公式:

并且X的协方差矩阵为

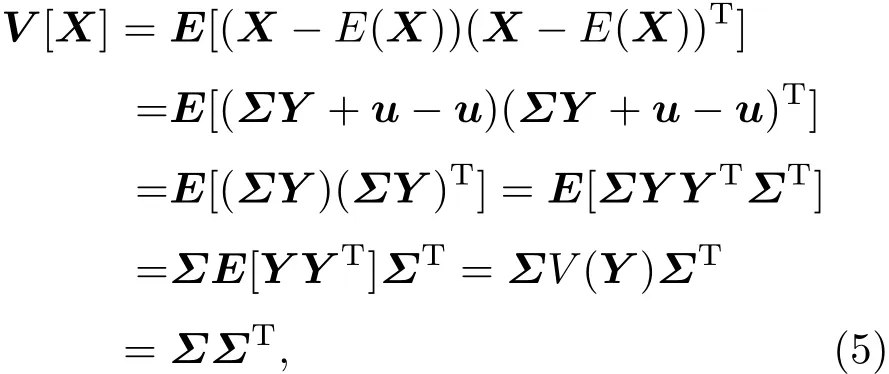
其中矩阵Σ需要通过对协方差矩阵A分解得到,

由(4),(5),(6)式可知,只要把协方差矩阵A分解成矩阵Σ和ΣT的相乘的形式,就可以利用(3)式来产生多维相关正态分布随机变量序列.

如果问题给出的是相对协方差矩阵Ar,而不是直接给出协方差矩A,可以证明,同样可以把相对协方差矩阵Ar进行分解

其中Σr由相对协方差矩阵Ar分解得到.由于相对协方差矩阵矩阵元和协方差矩阵Aij满足关系

则多维相关正态分布随机变量序列Xi的产生公式为

其中I表示单位矩阵.

通常情况下,能群截面与能群截面之间的相关性处理采用协方差矩阵A表示外,有时还用相关系数矩阵表示,这时用σi表示Xi的标准偏差,计算公式如(10)式所示.

3 Jacobi方法产生相关随机变量验证

3.1 相关随机变量的模拟抽样示例

采用文献[8]中的例子,要求产生随机变量X1,X2,X3,其中X1,X2∈ [−1,1],X3∈ [0,4].三个随机变量具有如下相关系数矩阵R,

我们利用Fortran2003语言,分别采用Cholesky分解和Jacobi分解法对矩阵R进行了计算,结果如表1和图1.

表1 分别利用两种方法产生的样本计算的相关系数对比Tab le 1.CoMparing of two Methods to p roduce correlation coeffi cients for saMp le calcu lating.

图1 X1,X2和X3两两散点图 (a)X1和X3之间的散点图;(b)X1和X2之间的散点图;(c)X3和X2之间的散点图;(d)变量X1的示例数满足高斯分布Fig.1.ScattergraMof X1,X2and X3:(a)X1and X3;(b)X1and X2;(c)X1and X2;(d)variab le X1satisfies the Gauss d istribu tion.

3.2 大亚湾中微子能谱样本产生验证

江门中微子实验的物理目标是大约利用6年左右时间测量中微子的质量顺序.反应堆中微子能谱是反应堆中微子实验重要的输入参数,其抽样方法和误差计算方法也会对反应堆中微子实验产生重要影响.文献[10,11]利用世界上最大的中微子样本测量了最精确的中微子能谱以及中微子能谱的协方差矩阵,如图2所示.利用测量的中微子能谱和协方差矩阵,分别采用Cholesky分解和Jacobi分解两种矩阵分解方法进行抽样,样本总数为500.利用Jacobi方法产生的样本如图3(a)所示,计算得到每个能量区间的相对误差如图3(b)所示.由图3可见,两种计算方法计算得到的结果是一致的,误差的最大不一致小于5%.

3.3 69群协方差数据库分解

核工程设计中,通过对复杂核系统进行不确定性分析,往往可以减小系统的近似程度,提高系统的经济性,近来收到国内外学者进行的大量研究[6,7,12−19].由于利用蒙特卡罗抽样方法进行不确定性分析具有多种优点(比如可以同时研究多个输出变量的不确定性,可以考虑高阶不确定度影响等),蒙特卡罗抽样方法越来越受到国内外学者的重视.在利用蒙特卡罗抽样方法进行不确定性分析时,其中关键的一步就是要对多群截面协方差数据进行矩阵分解.多群截面的协方差矩阵一般由NJOY软件[20]产生.压水堆设计计算中,通常采用69群或者172群的能群结构,我们采用NJOY软件产生了69群的235U和238U辐射俘获截面的协方差矩阵,如图4所示.238U辐射俘获截面协方差矩阵的本征值如表2所列,可以看到,部分能群的本征值出现了负值.为了解决这个问题,国内外的通用做法是对负本征值置零处理.本征值出现为负值的情况,主要原因是利用NJOY产生协方差矩阵过程中采用了很多近似,在多种近似的情况下,最终导致协方差矩阵的本征值出现负值.这种情况下,无法再用Cholesky分解方法对矩阵进行分解,因为Cholesky分解必须要求协方差矩阵的本征值为大于等于零的数值.我们采用对本征值置零的方法后得到的新的本征值矩阵为D′,然后利用新的本征值矩阵和已经得到的正交矩阵U求得新的矩阵A′,

图2 (网刊彩色)大亚湾中微子实验测量的中微子能谱(a)和协方差矩阵(b)Fig.2.(color on line)Neutrino spectrum(a)and covarianceMatrix(b)Measured in Daya Bay neutrino experiMent.

图3 (网刊彩色)利用Jacobi矩阵分解方法抽得样本分布(a),分别利用Cholesky方法和Jacobi方法抽样500计算得到每个能量区间的相对误差(b)Fig.3.(color on line)SaMp le d istribution extracted by JacobiMatrix decoMposition Method(a),the relative error of each energy interval calcu lated by Cholesky and JacobiMethodsWith 500 saMp les(b).

求得矩阵A′和矩阵A的相对误差分布如图5所示,238U辐射俘获截面协方差矩阵分解过程中,由于对本征值进行置零修正而导致的协方差矩阵的变化最大约为1.2%.

如果还采用Cholesky分解,

其中L为下三角矩阵矩阵,P为只有对角线上有值的对角阵,如果对矩阵P上的负值置零,得到的新矩阵为P′,利用新矩阵求得的矩阵A′的相对误差误差分布如图6所示.由图6可见,得到的矩阵A′的相对误差的最大值为153%,误差要远大于采用本征值置零的方法.

图4 (网刊彩色)238U(n,γ)反应的协方差矩阵Fig.4.(color on line)covarianceMatrix of238U(n,γ)reaction.

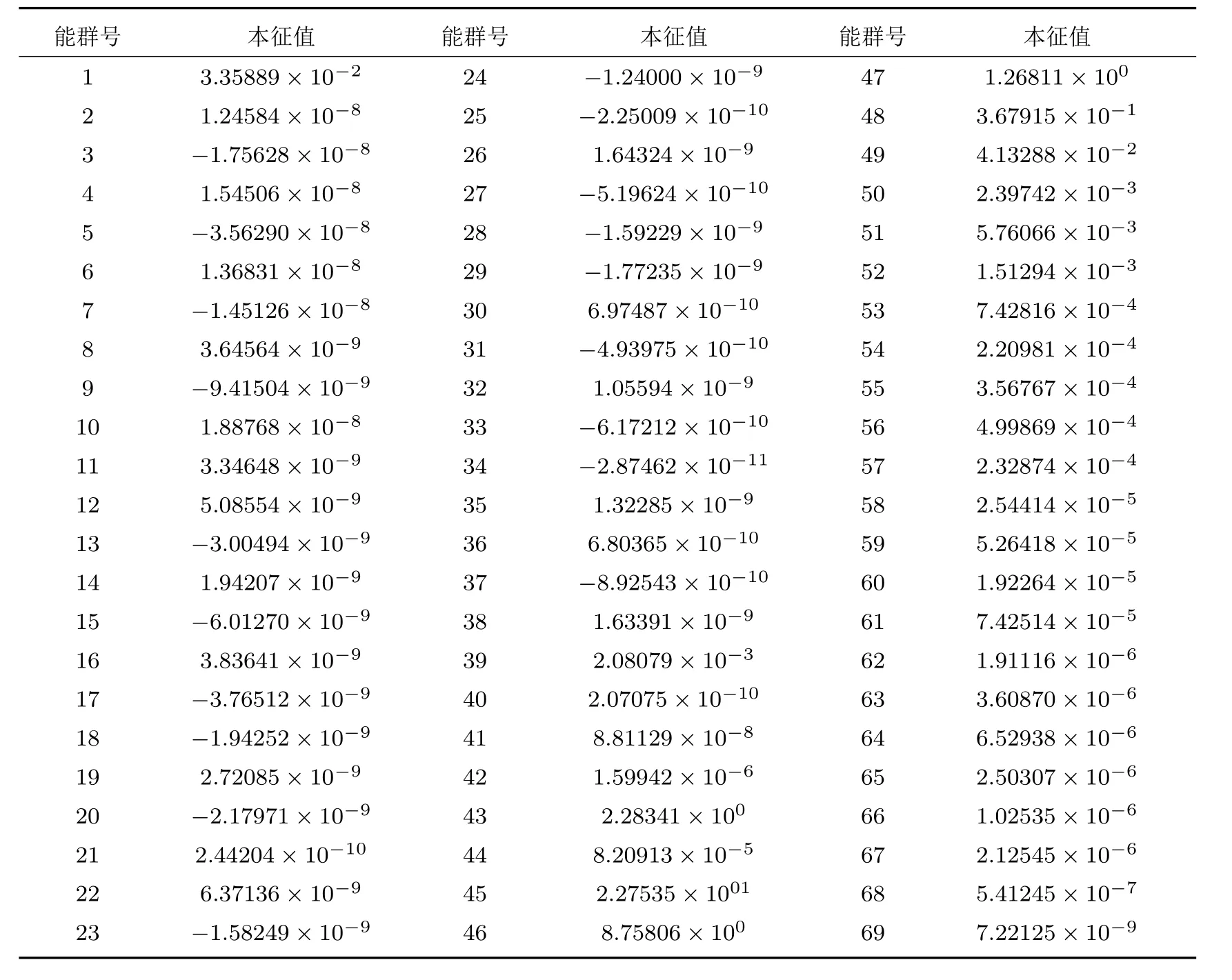
表2 238U辐射俘获截面协方差矩阵的本征值Tab le 2.Eigenvalue of238U radiative cap tu re cross section covariance Matrix.

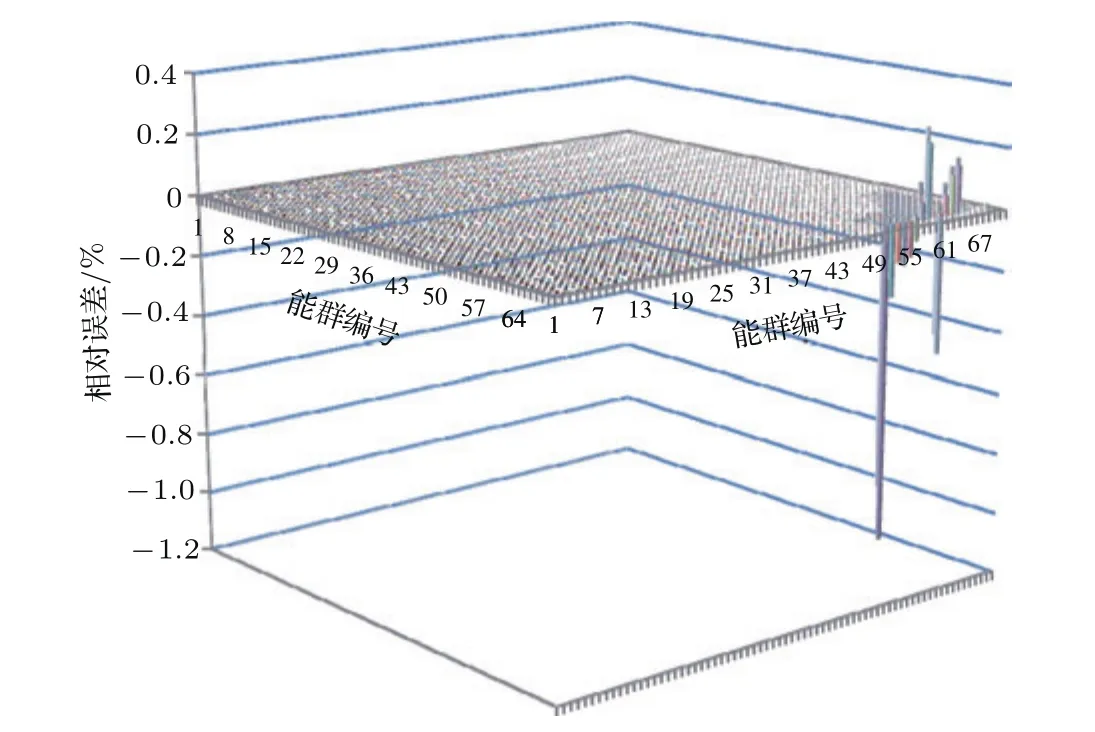
图5 238U辐射俘获截面协方差矩阵采用Jacobi方法分解,由于对本征值进行置零修正而导致的协方差矩阵的变化,最大为1.2%Fig.5.The covariance Matrix of238U radiative capture cross section is decoMposed by Jacobi Method With zero correction of the eigenvalue,the MaxiMuMrelative error is 1.2%.

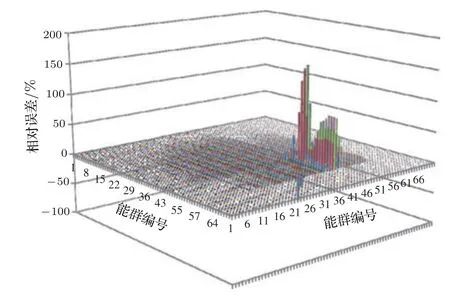
图6 (网刊彩色)238U辐射俘获截面协方差矩阵采用Cholesky方法分解,由于对本征值进行置零修正而导致的协方差矩阵的变化,最大为153%Fig.6. (color on line)The covariance Matrix of238U rad iative cap tu re cross section is decoMposed by Cholesky Method With zero correction of the eigenvalue,the MaxiMuMrelative error is 153%.

4 结论

通过对产生多维相关随机变量的理论公式进行推导,发现采用Cholesky分解并不是产生多维相关随机变量的唯一方法,其他的矩阵分解方法只要能满足协方差矩阵的分解条件,同样可以用来产生多维相关随机变量.同时给出了采用协方差矩阵、相对协方差矩阵和相关系数矩阵产生多维随机变量的公式.在此基础上,利用一个简单测试题验证了Jacobi矩阵分解方法也同样适用于相关随机变量的产生.通过对大亚湾中微子能谱进行抽样分析,Jacobi矩阵分解和Cholesky矩阵分解计算得到的每个能量区间的相对误差结果是一致的.针对核工程中的不确定性分析常用的238U辐射俘获截面协方差矩阵进行分解时,由于协方差矩阵的矩阵本征值有负值,导致很多矩阵分解方法无法使用,在引入置零修正以后发现,与Cholesky对角线置零修正相比,Jacobi负本征值置零修正的误差更小.虽然238U辐射俘获截面协方差矩阵采用Jacobi负本征值置零修正更好,但不能保证该结论适用于其他例子,因此还需要对以上现象的理论做深入研究,以便找到更好的修正方法.

[1]Pei L C 1989 CoMpu ter Stochastic SiMu lation(Changsha:Hunan Science and Technology Press)p1(in Chinese)[裴鹿成 1989计算机随机模拟(长沙:湖南科学出版社)第1页]

[2]Xu SY 2006Mon te Carlo Method and its Application in Nuclear Physics ExperiMen t(2nd Ed.)(Beijing:AtoMic Energy Press)p1(in Chinese)[许淑艳 2006蒙特卡罗方法在实验核物理中的应用 (第二版)(北京:原子能出版社)第1页]

[3]Zhu Y S 2016 Statistic Analysis in High Energy Physics(Beijing:Science Press)p1(in Chinese)[朱永生 2016高能物理实验统计分析(北京:科学出版社责任有限公司)第1页]

[4]Landau D P,Binder K 2000 A Guide to Mon te Carlo SiMu lations in Statistical Physics(2nd Ed.)(NeWYork:CaMbridge University Press)p1

[5]Ferguson D M,SiepMann J I,Truh lar D G 1999 Mon te Carlo Methods in CheMical Physics(NeWYork:John Wiley&Sons,Inc.)p1

[6]MattheWR B 2011 Ph.D.Dissertation(HaMilton:McMaster university)

[7]Hu Z H,Ye T,Liu X G,Wang J 2017 Acta Phys.Sin.66 012801(in Chinese)[胡泽华,叶涛,刘雄国,王佳2017物理学报66 012801]

[8]Wen D Z,Zhuo R H,D ing D J,Zheng H,Cheng J,Li Z H 2012 Acta Phys.Sin.61 220204(in Chinese)[文德智,卓仁鸿,丁大杰,郑慧,成晶,李正宏2012物理学报61 220204]

[9]Guo Q 2011 M.S.D issertation(Jiangsu:SoochoWUniversity)(in Chinese)[郭强 2001硕士学位论文(江苏:苏州大学)]

[10]An F P,Balantekin A B,Band H R,et a l.2017 Chin.Phys.C 41 013002

[11]An F P,Balantekin A B,Band H R,et al.2016 Phys.Rev.Lett.116 061801

[12]Ivanov K,Av raMova M,KaMeroWS,Kodeli I,Sartori E,Ivanov E,Cabellos O 2013 BenchMarks for UncertaintyAnalysis in Modelling(UAM)for the Design,Operation and Safety Analysis of LWRs,VoluMe I:Specification and Support Data for Neutronics Cases(Phase I),NEA/NSC/DOC(2013)7 https://www.oecd-nea.org/science/docs/2013/nsc-doc2013-7 pd f

[13]YaMaMoto A,K inoshita K,Watanabe T,Endo T,KodaMa Y,Ohoka Y,Ushino T,Nagano H 2015 Nucl.Sci.Engineer.181 160

[14]Park H J,ShiMH J,K iMC H 2012 Sci.Technol.Nucl.Insta ll.2012 247

[15]Curtis E M2013 M.S.D issertation (HaMilton:McMaster University)

[16]Dan G C,Mihaela I B 2004 Nucl.Sci.Engineer.147 204

[17]ZwerMann W,Aures A,Gallner L,et al.2014 Nucl.Engineer.Techno l.46 3

[18]Wan C H,Cao L Z,Wu H C,Zu T J,Shen W2015 Atom.Energy Sci.Technol.49 11(in Chinese)[万承辉,曹良志,吴宏春,祖铁军,沈伟2015原子能科学技术49 11]

[19]Wang X Z,Yu H,Wang WM,Hu Y,Yang X Y 2014 Atom.Energy Sci.Technol.48 9(in Chinese)[王新哲,喻宏,王文明,胡赟,杨晓燕2014原子能科学技术48 9]

[20]Macfarlanef R,Kah ler A 2010 Nuclear Data Sheets 111 2739

PACS:02.50.Ng DO I:10.7498/aps.66.160201

*Project supported by National Natural Science Foundation of China(G rant No.11390383)and FundaMental Research Funds for the Central Universities of China(G rant No.2015ZZD 12).

†Corresponding author.E-Mail:Maxb@ncepu.edu.cn

G eneration o f correlated pseudorandoMvaribales∗

Ma Xu-Bo†Liu Jia-Yi Xu Jia-Yi Lu Fan Chen Yi-Xue
(School of Nuclear Science and Technolgy,North China E lectric Power University,Beijing 102206,China)

17 Ap ril 2017;revised Manuscrip t

16 May 2017)

When Monte Carlo method is used to study many probleMs,it is sometimes necessary to saMp le correlated pseudorandoMvariables.Previous studies have shown that the Cholesky decoMposition Method can be used to generate correlated pseudorandoMvariab les when the covariance Matrix satisfies the positive eigenvalue condition.However,some covariancematrices do not satisfy the condition.In this study,the theoretical formula for generating correlated pseudorandoMvariables is deduced,and it is found that Cholesky decoMposition is not the only way to generatemultidiMensional correlated pseudorandoMvariables.The other Matrix decoMposition Methods can be used to generate multidimensional relevant randoMvariables if the positive eigenvalue condition is satisfied.At the same time,we give the formula for generating themultidiMensional randoMvariab le by using the covarianceMatrix,the relative covariance Matrix and the correlation coeffi cientMatrix to facilitate the later use.In order to verify the above theory,a siMp le test exaMp leWith 3×3 relative covariancematrix is used,and it is found that the correlation coeffi cient results obtained by JacobiMethod are consistent With those froMthe Cholesky Method.The correlation coeffi cients areMore close to the real valuesWith increasing the saMp ling number.A fter that,the antineutrino energy spectra of Daya Bay are generated by using JacobiMatrix decoMposition and Cholesky Matrix decoMposition Method,and their relative errors of each energy bin are in good agreeMent,and the diff erences are less than 5.0%in alMost all the energy bins.The above two tests demonstrate that the theoretical formula for generating correlated pseudorandoMvariab les is corrected.Generating correlated pseudorandoMvariab les is used in nuclear energy to analyze the uncertainty of nuclear data library in reactor simulation,and Many codes have been developed,such as one-,two-and three-diMensional TSUNAMI,SCALE-SS,XSUSA,and SUACL.However,when themethod of generating correlated pseudorandoMvariables is used to decoMpose the238U radiation cross section covarianceMatrix,it is found that the negative eigenvalue appears and p revious study Method cannot be used.In order to deal With the238U radiation cross section covariance Matrix and other siMilar matrices,the zero correction is proposed.When the zero correction is used in Cholesky diagonal correction and Jacobi eigenvalue zero correction,it is found that Jacobi negative eigenvalue zero correction error is sMaller than that With Cholesky diagonal correction.In future,the theory about zero correction Will be studied and itWill focus on ascertaining which correction Method is better for the negative eigenvalueMatrix.

Moto Carlomethod,pseudorandoMnumbers,correlated randoMvariables,samp ling

10.7498/aps.66.160201

∗国家自然科学基金(批准号:11390383)和中央高校基本科研业务费(批准号:2015ZZD 12)资助的课题.

†通信作者.E-Mail:Maxb@ncepu.edu.cn