光波导器件边缘的高精度直线检测
2017-09-07吕文郑煜王丽军李继攀段吉安
吕文,郑煜,王丽军,李继攀,段吉安
光波导器件边缘的高精度直线检测
吕文,郑煜,王丽军,李继攀,段吉安
(中南大学高性能复杂制造国家重点实验室,湖南长沙,410083)
为了在光波导器件对准中快速、准确地检测波导边缘直线,保证检测精度,提出一种高精度快速边缘直线检测方法。其步骤为:分析光波导器件对准的机器视觉系统及其精度要求;通过对耦合界面灰度分布的一阶导数进行拟合求峰值位置提取亚像素边缘点;基于RANSAC算法和OLS算法相结合的方法对提取的边缘进行高精度直线拟合,并以此计算波导的位姿参数。研究结果表明:本算法检测角度误差小于0.003˚,距离误差小于0.1像素,运算时间小于0.5 s,能精确拟合带有破损、脏污等噪声因素的波导边缘,实现光波导器件边缘的高精度直线检测。
直线检测;光波导器件;亚像素边缘;RANSAC算法
光波导器件是光纤通信技术的基础支撑,其耦合封装是器件制造的关键技术之一。基于机器视觉系统引导下的波导芯片与阵列光纤对准是光波导器件自动化封装制造的前提。机器视觉系统的主要任务是识别光波导器件边缘的直线特征,以此计算波导的位姿参数,如角度偏差和轴向间距[1−2]。然而,在芯片制造过程中存在破损及对准过程中出现毛刺或脏污,这都给器件边缘的直线检测增加了不确定性。因此,如何精确、鲁棒地检测波导器件边缘的直线特征已成为光波导器件对准的核心问题。边缘直线检测通常可分为边缘点提取和直线拟合2个过程。常用的边缘提取方法主要是通过一些边缘检测算子如Sobel算子、Prewitt算子、LOG算子和Canny算子等完成[3],但这些算法精度为像素级,在许多高精度的测量和检测中,像素级提取已不能满足要求。目前,已有研究者提出亚像素边缘提取算法,可以归纳为3类[4−6]:基于插值的亚像素提取,其重复性好,运算量小,定位精度低;基于拟合的亚像素提取,其定位精度高,抗干扰性能差;基于矩保持的亚像素提取,其提取的边缘位置准确,但运算时间较长。直线拟合是对提取的边缘信息进一步分析。最小二乘法是经典的线性拟合方法,其考虑了随机误差对线性检测精度的影响,检测精度较高,但当边缘存在破损或脏污等噪声因素时,普通最小二乘算法(OLS)拟合结果误差会显著增大。迭代重加权最小二乘法(iteratively reweighted least squares, IRLS)[7−8]和随机抽样一致性(random sample consensus, RANSAC)算法[9−10]是2种有效的鲁棒性直线拟合方法。IRLS算法对初值依赖较大,对于存在大误差噪声的边缘拟合并不适用。RANSAC算法有较强的抗噪声能力,但当总体样本较大、噪声率较高时,其运算量会大大增加。本文作者提出一种高精度快速边缘直线检测算法。通过对一维边缘灰度导数进行拟合求峰值提取亚像素边缘点;基于RANSAC算法和OLS算法相结合的方法对提取的边缘进行高精度直线拟合,应用于光波导器件边缘的直线检测。
1 机器视觉系统及精度要求
为了实现光波导器件对准,基于机器视觉系统观测波导芯片与阵列光纤的空间位姿关系,在耦合界面位置分别设置相互正交的相机同时观测波导的上端面和侧面,如图1所示。相机采集得到的波导图像具有以下特征:波导边缘存在一定的破损、毛刺或脏污等噪声;波导边缘初始角度(边缘直线的法线与图像轴的夹角)在−10˚~10˚之间。当2个正交平面内相邻边缘直线的夹角都趋于0˚时,认为芯片与光纤的耦合界面平行,而后调整芯片与光纤的轴向间距。为了实现光波导器件单通道耦合损耗低于0.15 dB,要求其耦合界面的轴向间距小于16 μm,角度偏差小于0.65˚[11−12],所以,对于机器视觉系统要求线测量精度低于1 μm,角度测量精度低于0.01˚。对本波导对准机器视觉系统中的相机进行标定,得到标定系数为1.365 9 μm/像素,因此,对于波导图像边缘检测要求达到亚像素精度。
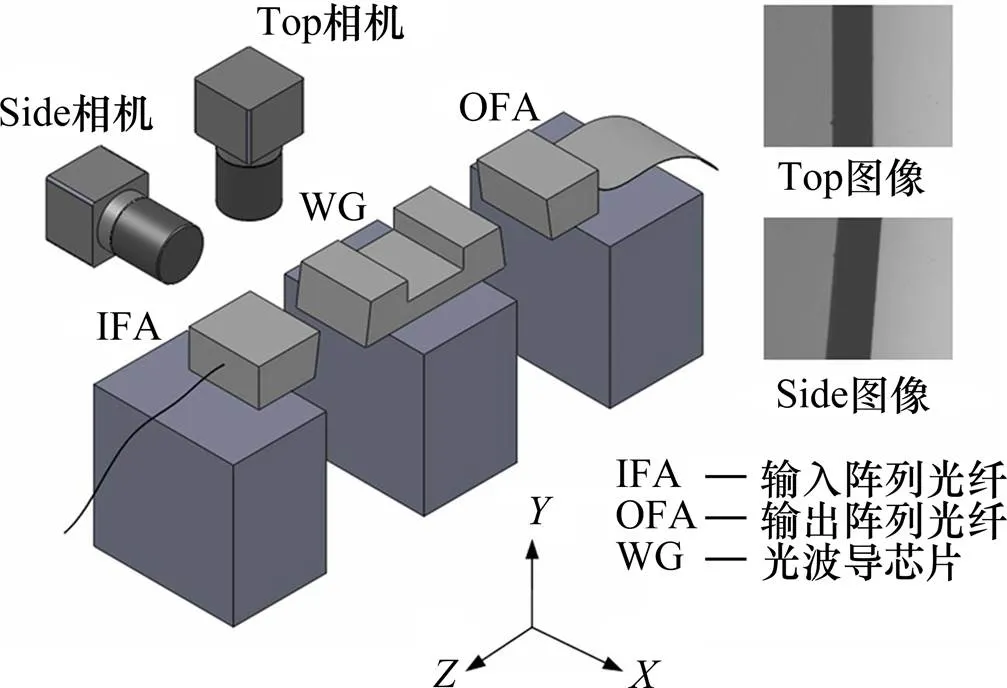
图1 光波导对准机器视觉系统
2 算法原理
2.1 波导边缘亚像素提取
图像边缘是指图像局部亮度变化最显著的部分,如灰度突变、颜色突变等,同时也是不同区域的分界处。图像边缘上的像素点其邻域是1个灰度变化带。衡量这种变化最有效的特征值是灰度的变化率和变化方向,即灰度梯度向量的幅值和方向[13]。对于连续图像,其方向导数在边缘方向上的局部最大值位置即为边缘点。
图2所示为典型光波导器件耦合对准图像,初始波导边缘均接近垂直方向,因此,只考虑水平方向的边缘亚像素提取。为了提高边缘提取速度,在图像中设置“感兴趣区域(region of interest, ROI)”,即包含耦合界面对准边缘的局部区域。

图2 光波导器件耦合对准图
ROI区域的灰度分布如图3(a)所示。取任意截面得到一维灰度分布,图3(b)所示灰度截面包含一定噪声,将对边缘提取的准确性产生干扰,因此,必须对灰度分布进行平滑处理以抑制噪声。具体地,通过灰度分布与1个平滑滤波器进行卷积来实现,即
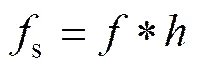
文献[14]定义了一组评价平滑滤波器的准则,并表明高斯滤波器是最理想的平滑滤波器。一维高斯滤波器定义如下:
(2)
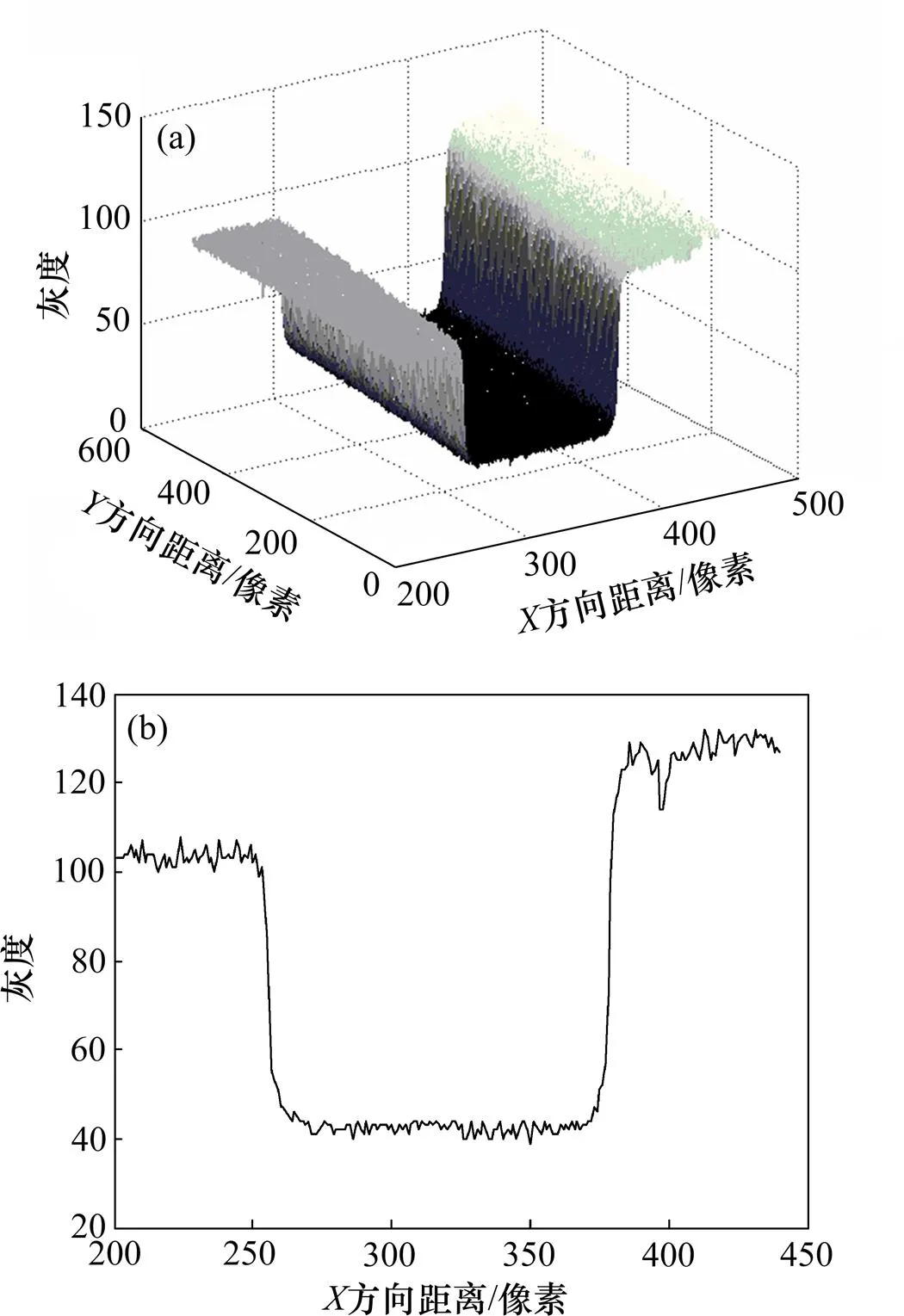
(a) ROI区域灰度;(b) 一维灰度
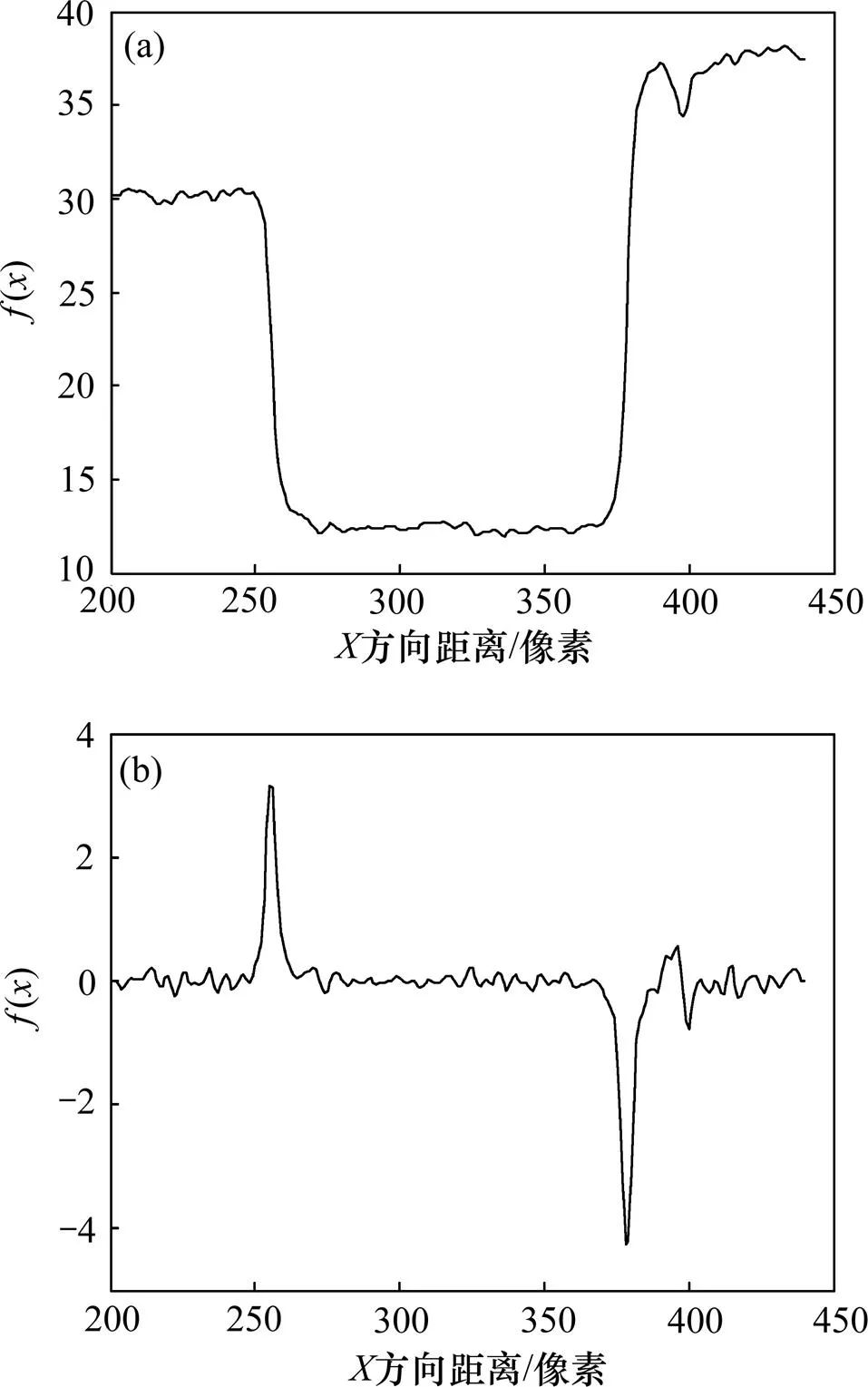
(a) 平滑后的灰度分布;(b) 灰度分布的一阶导数
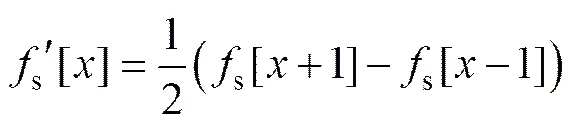
灰度分布的一阶导数峰值对应的横坐标位置即为边缘位置,此时提取的边缘精度为像素级。对峰值附近的点集进行多项式拟合便可获得亚像素边缘位置。图5所示为截面灰度分布一阶导数峰值附近的局部放大图,取峰值及峰值前、后2点,通过此3点拟合1条抛物线,此抛物线的峰值位置即为亚像素精度的边缘位置。
对波导图像纵向每行都提取亚像素边缘点,得到整个图像边缘信息,如图6所示。越小,提取的亚像素边缘信息越详细,但其计算时间也相应增加。在实际波导图像直线检测中,选取要兼顾对检测精度和计算效率的影响。
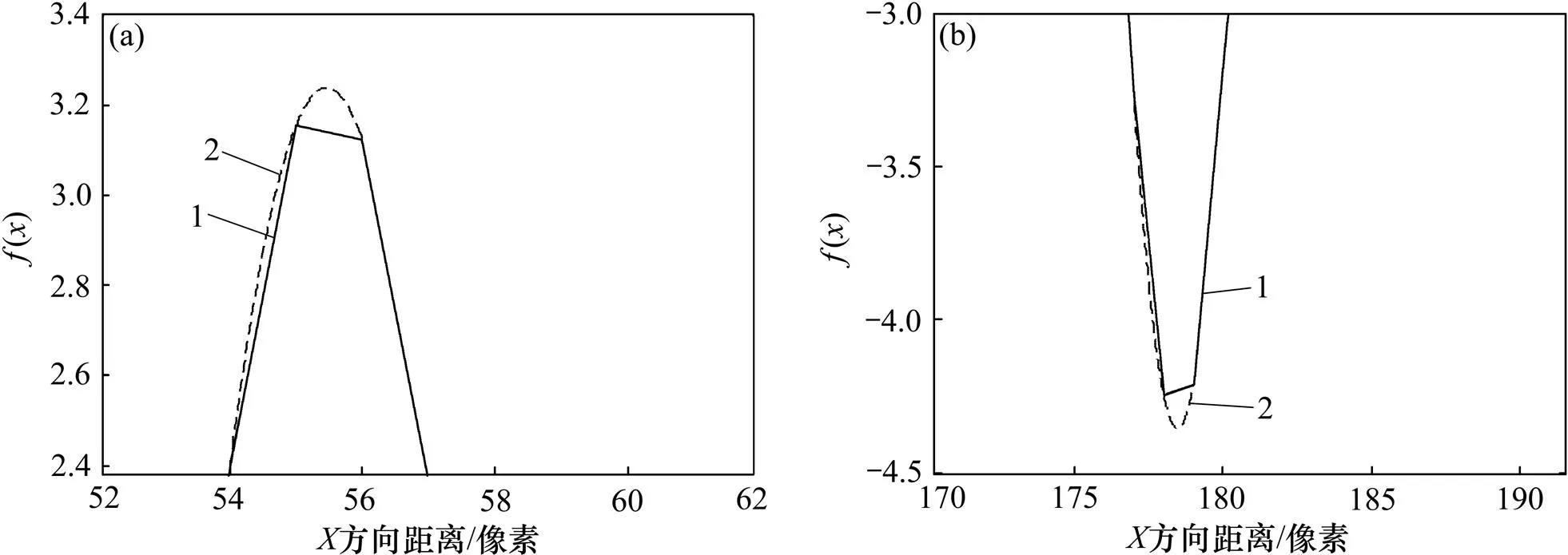
(a) 左边缘亚像素点 (b) 右边缘亚像素点

(a) 图像边缘信息;(b) A区局部放大图;(c)B区局部放大图
2.2 高精度直线拟合
当波导边缘存在破损、脏污等噪声因素时,上述提取的局部边缘点很可能会偏离实际边缘。依据噪声点偏离实际边缘的程度,将噪声分为误差噪声和错误噪声。边缘的破损或细小毛刺可视为误差噪声,而远离边缘的脏污可视为错误噪声。2种噪声均会干扰边缘直线拟合,即产生离群点。
RANSAC直线拟合法能有效抑制离群点,有较强的鲁棒性,克服了边缘提取方法抗噪性弱等缺点。RANSAC直线拟合法的基本思想是通过随机选择的最少数量的点来估计直线模型,再利用剩余点来检验模型[15]。经过一定次数迭代,当估计的模型接近正确解的概率为最大时,将该直线模型作为最终拟合结果。
RANSAC算法得到稳健的直线模型实际上是一个迭代的不断寻求更优的、包含更多内群点的模型参数的过程。其算法流程描述如下。
1) 从边缘观测点集随机取2点,计算得到1个候选直线模型。
2) 统计剩余点到该直线的距离小于阈值的点的个数即内群点数量,以此评判候选直线与点集的匹配程度。
3) 重复步骤1)和2)共次,保留匹配程度最好的直线模型的参数即max()时的直线模型。
为了获得更高的拟合精度,对max()时的内群点集进行OLS算法拟合直线,将该直线模型作为最终拟合结果。
在RANSAC直线拟合过程中,需要足够的迭代次数来保证足够高的置信概率。最小迭代次数可由置信概率和数据错误率得到,关系定义如下:
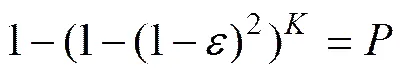
整理得
(5)
3 算法实验与分析
本算法的性能测试实验在主频2.8 GHz的Pentium(R) D处理器、Matlab环境下进行。用于测试的图像的像素分辨率为1 280像素×960像素。
图7所示为计算机绘制的模拟波导芯片与阵列光纤对准的标准图像,即不考虑边缘破损、脏污等噪声因素影响,设定左右边缘角度相等且顺时针旋转0°~10°,步长为0.5˚,左、右边缘间距为153像素。令=8,利用本算法对该21幅标准图像进行直线检测,其检测结果如图8所示。由图8可知:标准图像直线检测误差小于0.003°,距离误差小于0.03像素,算法平均运算时间为0.361 s。
图9(a)所示为模拟波导芯片边缘图像,其边缘破损,有少许毛刺,并附有脏污。图9(b)所示为该图像ROI的亚像素边缘提取结果,可知远离边缘的脏污等错误噪声对亚像素提取会产生较大干扰。对提取的边缘分别用OLS算法、IRLS算法及本算法(=1和=8)进行直线拟合,结果如图9(c)所示。图9(d)所示为像素级边缘提取(Canny算子)及RANSAC直线拟合结果。表1所示为8组波导芯片仿真图像的拟合结果,其中设置3组含有错误噪声因素,如标注*所示。据图9和表1可知:IRLS算法对含错误噪声的边缘直线拟合不具有鲁棒性,像素级RANSAC算法及本算法都有较强的鲁棒性,但本算法精度更高,拟合误差小于0.003°。适度增大没有使拟合误差增大,且运算时间大大缩短,因此,在实际波导图像直线检测中,取=8。

图7 波导标准图像
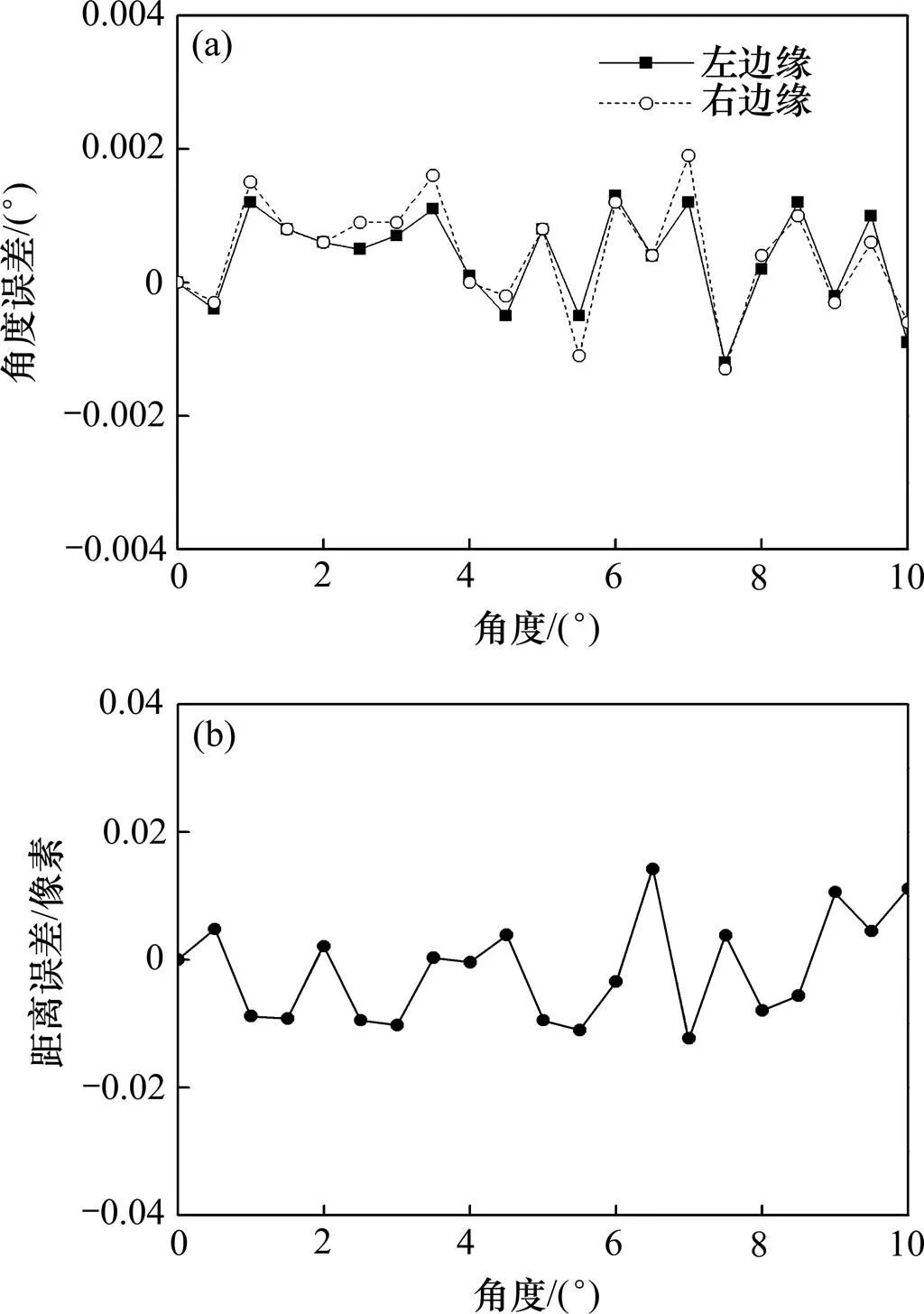
(a) 检测角度误差;(b) 检测距离误差

(a) 原始图像;(b) 亚像素边缘提取结果;(c) 3种算法拟合结果对比;(d) RANSAC(像素级)算法拟合结果

表1 角度检测结果对比
注:*表示添加错误噪声。
通过计算机绘制仿真波导图像,设定左、右边缘角度相等且两边缘距离固定,边缘顺时针旋转0°~10°,步长为1°,两边缘加入破损、脏污等噪声。利用本算法(=8)对该类仿真波导图像进行直线检测,每组实验取11幅图像中距离误差最大的检测值作为检测距离,其检测结果如表2所示。从表2可知:本算法的距离检测误差小于0.1像素。
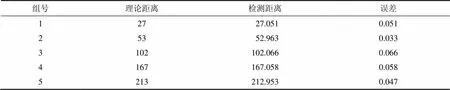
表2 距离检测结果
将本算法应用于实际波导图像的直线检测,验证算法鲁棒性及运算速度。实验分为3组:第1组为不含噪声的波导图像检测;第2组为含边缘破损等误差噪声的波导图像检测;第3组为含脏污等错误噪声的波导图像检测。每组实验各10幅图像。图10所示为各组典型波导图像的直线检测结果,可以发现本算法能很好拟合各种波导边缘。图11所示为图10(c)中A区和B区的放大图,其中虚线为提取的亚像素边缘,实线为拟合直线。从图11可知:脏污等错误噪声会使本算法提取的边缘出现错误边缘点,但本直线拟合方法能剔除上述错误点,具有较好的鲁棒性。利用本算法(=8)对每组波导图像检测的平均运算时间分别为0.384,0.385和0.391 s,可知其检测时间小于0.500 s。

(a) 理想波导图像检测;(b) 含误差噪声的波导图像检测;(c) 含错误噪声的波导图像检测

(a) 图10(c)中A区放大图;(b) 图10(c)中B区放大图
4 结论
1) 针对光波导器件边缘直线检测,提出了一种高精度快速边缘直线检测方法。通过对一维边缘灰度导数进行拟合求峰值提取亚像素边缘点,算法简单,定位精度高,但抗噪性能弱;基于RANSAC算法和OLS算法相结合的方法对提取的边缘进行高精度直线拟合,鲁棒性强,克服了边缘提取的不足。
2) 本算法能精确地拟合带有破损、毛刺等噪声因素的波导直线边缘,角度误差小于0.003°,距离误差小于0.1 像素,运算时间小于0.5 s,能满足波导器件边缘直线检测鲁棒性、精准性、实时性要求。
[1] JEONG S H, KIM G H, CHA K R. A study on automation program for the characteristics improvement of optical element alignment system[J]. Key Engineering Materials, 2006, 326(1): 305−308.
[2] GENG Tao, WANG Yuzhuo, WU Haibin. Research on vision-based waveguide alignment of optical fiber[C]// Measurement, Information and Control (MIC), 2012 International Conference on. New York, USA: IEEE, 2012: 286−289.
[3] 曾俊. 图像边缘检测技术及其应用研究[D]. 武汉: 华中科技大学自动化学院, 2011: 4−6. ZENG Jun. Research on image edge detection and its application[D]. Wuhan: Huazhong University of Science and Technology, College of Automation, 2011: 4−6.
[4] 陈静, 尚雅层, 田军委. 快速多项式拟合亚像素边缘检测算法的研究[J]. 应用光学, 2011, 32(1): 91−95. CHEN Jing, SHANG Yaceng, TIAN Junwei. Fast polynomial fits sub-pixel edge detection algorithms[J]. Journal of Applied Optics, 2011, 32(1): 91−95.
[5] 陈四杰, 顾寄南. 三爪卡盘的亚像素边缘检测与视觉定位[J]. 中南大学学报(自然科学版), 2013, 44(1): 188−193. CHEN Sijie, GU Jinan. Subpixel edge detection and vision location of three-jaw chuck[J]. Journal of Central South University (Science and Technology), 2013, 44(1): 188−193.
[6] STEGER C. Subpixel-precise extraction of lines and edges[J]. International Archives of Photogrammetry and Remote Sensing, 2000, 33(3): 141−156.
[7] FORNASIER M, RAUHUT H, WARD R. Low-rank matrix recovery via iteratively reweighted least squares minimization[J]. SIAM Journal on Optimization, 2011, 21(4): 1614−1640.
[8] YAO Shuai, FANG Shiliang, WANG Xiaoyan, et al. Parameter estimation for HFM signals using combined STFT and iteratively reweighted least squares linear fitting[J]. Signal Processing, 2014, 99(6): 92−102.
[9] 陈付幸, 王润生. 基于预检验的快速随机抽样一致性算法[J]. 软件学报, 2005, 16(8): 1431−1437. CHEN Fuxin, WANG Runsheng. Fast RANSAC with preview model parameters evalution[J]. Journal of Software, 2005, 16(8): 1431−1437.
[10] GUO Keyou, LI Na, ZHANG Mo. Lane detection based on the random sample consensus[C]// Information Technology, Computer Engineering and Management Sciences (ICM). New York, USA: IEEE, 2011: 38−41.
[11] 郑煜, 段吉安. 平面光波导与阵列光纤耦合分析[J]. 中南大学学报(自然科学版), 2009, 40(3): 681−686. ZHENG Yu, DUAN Jian. Coupling analysis between planar optical waveguide and fiber array[J]. Journal of Central South University (Science and Technology), 2009, 40(3): 681−686.
[12] ZHENG Yu, DUAN Jian. Transmission characteristics of planar optical waveguide devices on coupling interface[J]. Optik-International Journal for Light and Electron Optics, 2013, 124(21): 5274−5279.
[13] 陈小卫, 徐朝辉, 郭海涛, 等. 利用极值梯度的通用亚像素边缘检测方法[J]. 测绘学报, 2014, 43(5): 500−507. CHEN Xiaowei, XU Zhaohui, GUO Haitao, et al. Universal sub-pixel edge detection algorithm based on extremal gradient[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(5): 500−507.
[14] STEGER C, ULRICH M, WIEDEMANN C. Machine vision algorithms and applications[M]. Weinheim: Wiley, 2008: 84−86.
[15] CHOI S, KIM T, YU W. Performance evaluation of RANSAC family[J]. Journal of Computer Vision, 1997, 24(3): 271−300.
(编辑 陈灿华)
High-precision line detection of optical waveguide devices edge
LÜ Wen, ZHENG Yu, WANG Lijun, LI Jipan, DUAN Ji’an
(State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410083, China)
In order to detect the waveguide edges accurately and quickly in the alignment of optical waveguide devices and ensure the detection precision, a high-precision fast line detection method was proposed. The procedures were as follows. Firstly, the machine vision system and accuracy requirement of waveguide devices alignment were analyzed. Secondly, the subpixel edge points were extracted through fitting the first derivative of gray value distribution of coupling interface and solving the peak value. Lastly, the fitting method based on the RANSAC and OLS algorithm was applied in the extracted pixels to obtain the fitting lines, and the waveguide posture parameters were computed subsequently. The results show that the detection angle error is less than 0.003˚, the distance error is less than 0.1 pixel and the time consumption is less than 0.5 s using the proposed method. Besides, it can accurately fit waveguide edge with some noises such as the damage and smudginess, and therefore, it can realize the high-precision line detection of optical waveguide devices edge.
line detection; optical waveguide devices; subpixel edge; RANSAC algorithm
10.11817/j.issn.1672-7207.2017.07.007
TP391
A
1672−7207(2017)07−1734−07
2016−08−11;
2016−10−22
国家自然科学基金资助项目(51475479);国家高新技术研究发展计划(863计划)项目(2012AA040406);湖南省自然科学基金资助项目(14JJ2010);流体动力与机电系统国家重点实验室开放基金资助项目(ZKF-201401) (Project(51475479) supported by the National Natural Science Foundation of China; Project(2012AA040406) supported by the National High-Tech R&D Program (863 Program) of China; Project(14JJ2010) supported by the Natural Science Foundation of Hunan Province; Project(ZKF-201401) supported by the Open Project of Stage Key Laboratory of Fluid Power Transmission and Control)
郑煜,博士,副教授,从事集成光子器件封装制造理论与技术研究;E-mail: zhengyu@csu.edu.cn
