多对十字脊波导传输特性的分析研究
2012-03-12张黎明姬川
张黎明 姬川
(郑州工业贸易学校电子与信息工程系,河南 郑州 450007)
在脊波导由Cohn在1947年提出以后就备受人们关注,与传统的矩形波导相比,脊波导有其独到的特性。本文主要是应用有限元法讨论了多对十字波导的变形对传输特性的影响,综合分析了两个脊分别位于对称位置时的十字波导的传输特性,计算十字脊波导在TE模式下的截止波长和单模带宽,研究归纳脊位置c的变化对变形多对脊波导截止波长 和单模带BW的影响,从而对变形多对脊波导的应用和研究提供有价值的参考。
1 基本原理及方法
有限元法已广泛应用于电磁场数值计算问题,根据Maxwell(麦克斯韦)方程
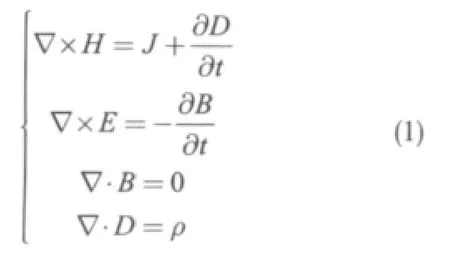
化简为Helmholtz方程,对于TE模φ= Hz,∂φ/∂n=0在波导壁上满足齐次Neumann边界条件∂,根据有限元理论分析,对于三角单元剖分的场域,可推导出下列本征值矩阵方程

其中A和B均为N×N阶方阵,N为节点数的总和,φ为变量φ的列向量,代表有限元剖分后各节点的φ值。k2c表示待求的特征值,求解特征值方程,得到的最小非负特征值就是主模的截止波数kc,得到的第2个最小非负特征值就是第1个高次模的截止波数,这样就可以得到脊波导的截止特性与单模带宽特性。
2 数值计算结果及分析
2.1 截止波长
Fig.1和Fig.2分别给出十字波导在脊位置c变化时,s/a和d/b固定时,c与归一化截止波长λc/a的关系曲线图和在TE模式的主模截止波长(λc)和第一高次模(λc1)的比值即:BW=λc/λc1单模带宽BW与c/a关系图,且脊的几何尺寸连续变化,其中b/a=0.45。
2.1.1 多对十字波导归一化截止波长λc/a的变化范围比较集中,大都分布在2.0的周围。单模带宽BW的变化范围比较集中,大都分布在2.0的周围。
2.1.2 多对十字波导退化为双脊波导的形状,在s/a,d/b为定值时归一化截止波长λc/ a随着c/a的增大而减小;单模带宽BW随着c/a的增大而先增大后减小。在c/a取定值时,随着s/a,d/b的增大归一化截止波长λc/a而增大,带宽BW随着s/a,d/b的增加而减小。
2.1.3 多对十字波导在c=0,0.05,0.1时,在c=0时,多对十字波导退化为双脊波导的形状。当s/a<0.4时,归一化截止波长λc/a随着s/a的增加而增加;当s/a≥0.4时,归一化截止波长λc/a随着s/a的增加而减小。在c= 0.05,0.1时。当s/a<0.3时,归一化截止波长λc/ a随着s/a的增加而增加;当s/a≥0.3时,归一化截止波长λc/a随着s/a的增加而减小。当s/ a固定时,单模带宽BW随着d/b(d/b=0.1除外)的增大逐渐减小,并在d/b=0.1时取得最大值;当d/b固定时,单模带宽BW随着s/a(s/ a=0.1除外)的增大而减小。
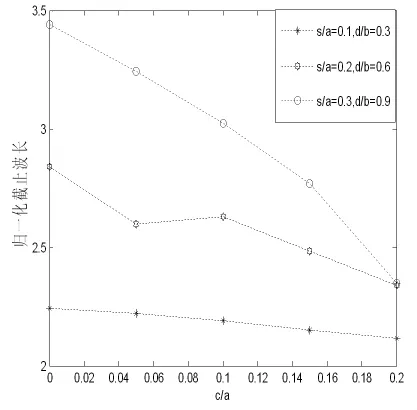
Fig.1 The curve corresponding to c and in multi cross ridged waveguide
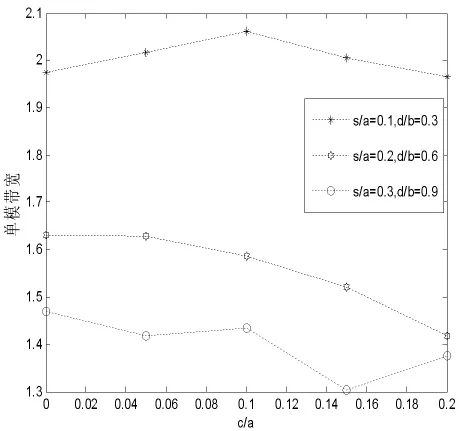
Fig.2 The curve corresponding to c and BW in multi cross ridged waveguide
2.1.4 多对十字波导在c=0.15时。归一化截止波长λc/a随着s/a的增加而先增加后减小,其中s/a=0.2是一个分界点。c=0.2时,当d/b<0.4时,归一化截止波长λc/a随着s/a的增加而减小;当d/b≥0.4时归一化截止波长λc/a随着s/a的增加而增加。在c=0.25时,归一化截止波长λc/a随着s/a的增加而减小。多对十字波导在c=0.15,0.2,0.25时。 当s/a= 0.1,d/b>0.1时,单模带宽BW随着d/b的增大而逐渐减小;当s/a=0.2,0.3时,单模带宽BW随着d/b的增大而逐渐减小,并在d/b=0.1时取得最大值。在c=0.3,0.35,0.4时。当s/a固定时,单模带宽BW随着d/b的增大而逐渐减小,并在d/b=0.1时取得最大值。
结论
本文采用有限元的计算方法研究了多对十字波导脊的位置发生变时的传输特性即归一化截止波长、单模带宽,通过对多对十字波导的截止波长和单模带宽的计算,可以看出:脊位于中间的多对十字波导比脊位于中间的多对双脊波导有更短的截止波长,更窄的单模带宽;双脊波导比多对双脊波有更长的的归一化截止波长,较宽的单模带宽;多对十字脊波导比十字波导有更长的归一化截止波长,较宽的单模带宽。通过这些研究表明:可以扩大脊波导传输特性的调节范围,能够对以后变形双脊波导的应用和研究提供有价值的参考,这对实际的微波和毫米波工程的发展研究提供了有价值的理论依据。
[1]XIAO ZHOGN QIU,CHAGN YIGN XIAGN,CUI DE WANG.FEM analysis on double-ridged waveguide eigenvalue of asymmetrical rideg site[J].Joumal of Chongqing Institute of Technology (Natural Science). 2008,22(5):104-107.(in chinese)
[2]ZHAO XIA,CHEN XIAO QIANG.Study of transmission characters of two kinds of new double-ridge waveguide[J].Radio-frequency engineering.2011.41(1)35-37.(in chinese)
[3]ZHAGN LI MING,LU MAI,CHEN XIAO QING.Study of Transmission Characters of Two Kinds of Deformed Double-ridge Waveguide[J].laser Technology.2009,33(3):333-336. (in chinese)
