化学核心素养之“模型认知”能力的测评研究

2017-09-06杨玉琴

化学教学 2017年7期

杨玉琴

摘要：界定了“模型认知”能力其及水平层次，应用Rasch模型开发和优化了测量工具。根据大样本测试数据对中学生“模型认知”能力现状进行了分析。结果显示，中学生的“模型认知”能力平均水平较弱，高一学生与高二学生之间无显著性差异，但皆与高三学生之间存在显著性差异，男生的水平显著高于女生。

关键词：“模型认知”能力；Rasch模型；测量和评价

文章编号：1005–6629（2017）7–0009–06 中图分类号：G633.8 文献标识码：B

1 问题的提出

在自然科学研究中，当客观对象并不能直接研究时，在进行了一定的观察、实验和对所获得的科学事实进行初步的概括之后，常常要利用想象、抽象、类比等方法，建构一个简化的又能集中反映客体本质关系的模型，并通过对模型的研究揭示原型客体的形态、本质和特征，此即模型方法[1]。化学是在原子、分子水平上研究物质性质及其变化的科学，原子、分子不可见，化学客观规律、物质性质及其变化的解释亦十分抽象，所以化学家需要通过建构模型加以认知和把握。通过模型，化学家可以“看到”他们所试图研究的实体或过程，据此进行实验设计和探索活动，有力支持他们的思维推理和知识建构[2]。

模型（model）与建模（modeling）是科学发展的重要元素，也是科学学习中不可或缺的认知与能力[3]。化学学习中的模型认知活动能促使学生全面深刻地理解化学模型的性质、作用、使用范围及其局限性等，并学会建构、检验模型，使用多种模型来表达、解释同一现象等[4]。美国《下一代科学教育标准》将“建构和应用模型”作为8个重要的科学与工程实践活动之一。我国目前进行的高中化学课程标准修订中亦将“模型认知”作为化学核心素养的重要组成部分[5]。对学生模型认知能力的测量与评价将有助于我们认识学生能力发展现状，为改进教学提供证据。

2 研究的理论框架

2.1 “模型认知”能力的界定

化学中的模型更多的是以观念形态描述原型的某些特征、性质、规律的抽象概念或理论模型，如分子、原子模型，理想气体模型，有效碰撞理论等等，所以我们将模型方法看成是一种科学认知方式。中学生的“模型认知”能力是指能够运用模型描述化学研究对象、解释化学现象和规律、预测可能的结果，并能够建构模型展示自己对化学事实的理解和解释的能力。

2.2 “模型认知”能力水平的构建

国外课程标准对“模型”的学习要求涉及到对模型本身的认识和理解、运用多种模型去表征和解释现象以及建构模型并评价模型等。综合国外对于“模型”学习进程的研究以及课程文件中对“模型”学习要求的规定，参照布卢姆教育目标分类学（修订版）对认知维度的划分，将“模型认知”能力水平划分为以下由低到高的4个水平：

水平1：认识模型。学生认识化学中的主要模型，并能以适当的方式表征模型。

水平2：理解模型。学生理解模型描述的对象、模型的本质、模型的性质等。

水平3：运用模型。学生能够利用模型描述物理或化学变化过程，解释化学事实，根据模型预测物质的性质和变化等。

水平4：建构模型。学生能够建构模型来展示和解释现象是如何发生的，讨论模型的适用范围和局限性，根据证据或批判性思维精致模型以提高模型的解释力等。

2.3 “模型认知”能力测量原理

以项目反应理论之Rasch模型作为测量工具开发、设计的框架。通过项目和被试信度、评分者一致性、误差、分离度等指标分析和检验工具的信度，通过单维性检验、项目-被试对应、数据-模型拟合、点-测量相关、选项反应模式及評分等级概率结构等指标来分析和检验工具的效度。

3 研究方法

根据“模型认知”能力从低到高的4个水平要求，编制测量工具。运用Rasch模型分析软件Bond & Fox Steps1.0.0对工具的信度、效度等进行分析，并对测量工具进行修改和优化，直至工具符合Rasch模型要求，再进行大样本测试。

3.1 研究工具

经过两轮试测及Rasch模型检验、优化后，形成了如表1所示的测验卷（以下简称M测验卷），其中M1～M14是选择题，M15～M20是建构反应题。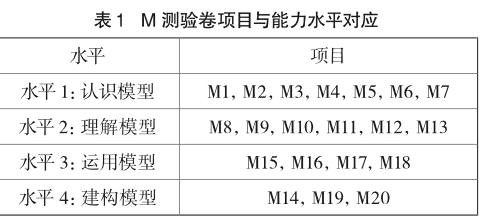

具体项目与模型认知能力水平的对应如表1所示，以下各举一例作简要分析说明。

例1 下图表示封闭在某容器中的少量液态水的微观示意图（容器的活塞可以左右移动）。煮沸后，液态水变成水蒸气。在这一过程中，发生的变化是（）

例2 以下关于原子的说法正确的是（）

A.在高倍显微镜下我们可以看到原子

B.原子是球形的

C.原子核外电子都是同样大小的

D.原子核外最外层有一层壳

说明：该题属于“水平2：理解模型”能力的考查内容，旨在考查学生对模型所描述的对象及其本质的理解。

例3 如图，将盛有浓氨水的烧杯（B）及盛有蒸馏水和酚酞的烧杯（A）同罩于一个大烧杯中，一会儿烧杯A中由无色变为红色。你能用图示的方法解释这一现象吗？可辅以一定的文字说明。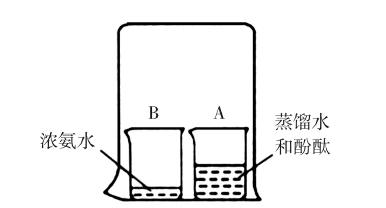

说明：该题属于“水平3：运用模型”能力的考查内容，旨在考查学生运用模型解释现象的能力。这是一道开放题，要求学生对发生的现象进行解释，学生需要使用图画配以文字说明加以表达，以充分反映学生头脑中关于化学反应的心智模型。本题并没有限定学生运用什么样的模型表征方式进行回答，学生运用模型的能力越高，越能够运用涉及化学反应微观本质的模型进行回答，越能够运用多种模型表征方式（符号的、语言的、图示的）来进行解释。

例4 燃素说是形成于17世纪末、18世纪初的一个解释燃烧现象甚至整个化学的理论模型。燃素说假定可燃烧的物质包含着燃素，以解释一切燃烧现象乃至所有的化学变化。如，“金属煅烧，逸去燃素而留下灰渣；灰渣与富有燃素的木炭共热，又还原为金属；金属溶于酸，则放出燃素（氢气），而留下灰渣等”。

如图所示，将精确测定质量的汞浮于一种液体之上，并用玻璃罩将其罩住，利用凸透镜聚集太阳光对玻璃罩内的汞加热。

（1）根据燃素理论模型，在该实验中应该出现的现象是什么？但你认为实际出现的现象会是什么？

（2）该实验现象与燃素模型所预测的现象并不一致，请你利用一种与燃素理论不同的模型来解释。

（3）为了证明你所利用的模型是正确的，请具体说明你会如何做。

说明：该题属于“水平4：建构模型”能力的考查内容，旨在考查学生能否根据提供的化学事实建构模型来展示和解释现象是如何发生的，讨论当预测现象与实际现象并不一致时如何改进模型，并能够根据证据利用批判性思维精致模型以提高模型的解释力。

3.2 研究样本

本研究共进行了三轮测验，被试组成如表2所示。第一轮试测用于初步考察测量工具的质量。经过Rasch模型检验分析后，对工具进行修改，再进行第二轮试测，根据第二轮试测结果的质量分析决定修改后的测验卷能否用于大样本测试。因第一轮、第二轮试测主要用于考察工具的质量，所用样本较小，也没有从高三年级中选择被试。大样本测试采取分层抽样的形式，在某省选取了三所不同层次的中学作为样本来源学校，分别在高一、高二、高三随机抽取被试。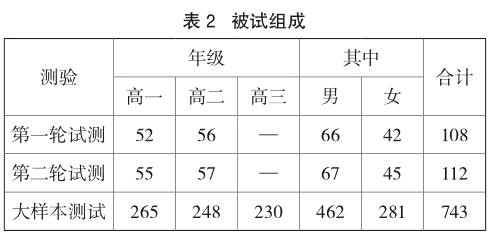

3.3 数据分析

运用Bond & Fox steps1.0.0分析测验工具的信、效度，将项目难度与学生能力转换成具有等距意义的logit分，再运用SPSS18.0软件进行统计分析。因篇幅有限，以下只呈现第三轮测试结果的分析。

4 结果分析

4.1 测量工具信、效度分析

如表3所示的总体统计数据显示，项目估计的标准误较小，被试和项目的数据拟合指數都较为理想，MNSQ都在理想值1附近，ZSTD亦在理想值0左右，说明测验与理论模型的期望较为吻合；项目信度接近1，分离度较大，说明项目能较好地区分不同能力的被试；被试的信度大于0.5，分离度较大，说明被试的能力分布较为分散，有一定的层次性。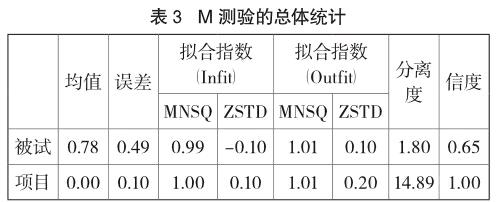

图1所示的单维性检验结果表明，只有AM04、a-M17略超出-0.4～0.4的范围，说明工具测量的皆为学生的一种主要心理特质——模型认知能力，符合Rasch模型的基本假设。项目—被试对应图（图2）显示，测试题分布较广，显示出明显的难度层次结构。各项目的难度水平与预期假设基本一致，学生能力分布较为理想，近似正态分布。各个项目的拟合、误差统计结果亦显示，除了M19的点测量相关较低外，绝大多数项目的估计误差都很小，项目拟合指数在许可范围内，点测量相关较高[6]。

综上可知，测量工具具有良好的信度和效度。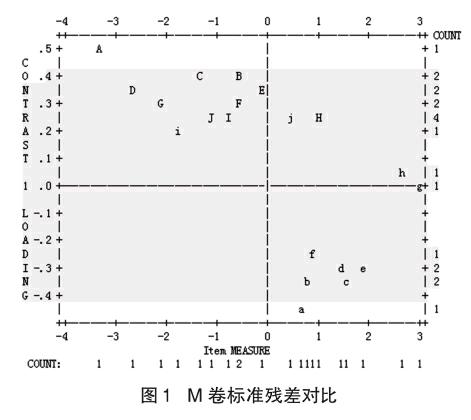

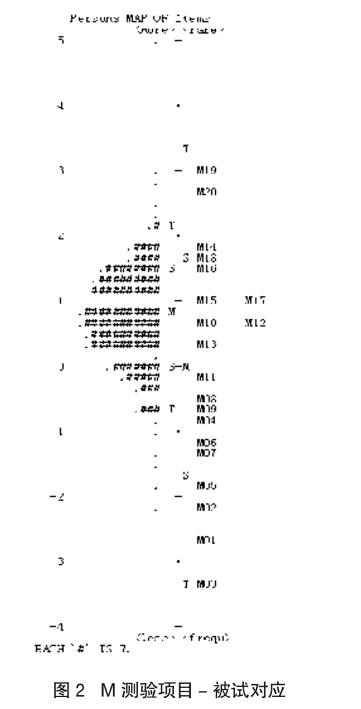
4.2 学生“模型认知”能力分析

4.2.1 不同年级学生测验成绩比较分析

（1）总体比较

表4是三个年级模型认知能力测验的描述性统计结果。最高值出现在高二，最低值出现在高三，高二年级的全距最大。而高二年级的均分比高一年级略小，高三年级的均分最大。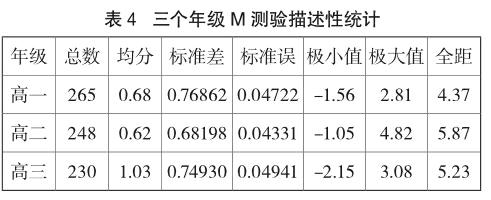

进一步检验三组均数差异的显著性，结果如表5所示，1、3组之间的相伴概率为0.000，2、3组之间的相伴概率为0.000，皆小于极显著性水平0.01，具有显著性差别。而1、2组之间的相伴概率为0.341，大于显著性水平，说明1、2组之间没有显著性差别。由以上统计分析可知，对于“模型认知”能力而言，高一年级的平均水平虽略高于高二年级，但并没有显著性差异，而高一年级与高三年级、高二年级与高三年级皆具有显著性差异。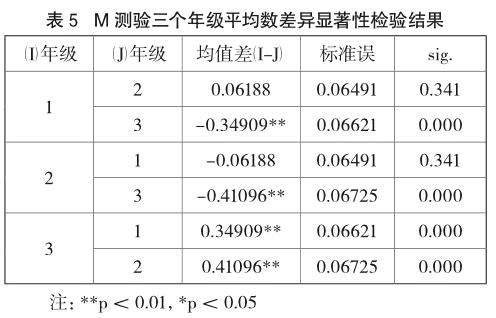

（2）在各个水平层次上的比较

Rasch模型通过将原始分转换为logit分，从而将被试能力、项目难度放在同一把量尺上进行比较。将M卷中各个项目的难度估计进行平均可得到每个水平的难度平均值，如表6所示，以此平均值作为判断学生“模型认知”能力水平的依据。当学生的能力值低于-1.88时，则认为学生的能力水平低于水平1；当学生的能力值为-1.88～0.11时，则位于水平1；当学生的能力值为0.11～1.26时，则位于水平2；当学生的能力值为1.26～2.51时，则位于水平3；当学生的能力值大于2.51时，则位于水平4。