大豆期货价格预测实证研究*

滕永平，周婷婷

（沈阳工业大学经济学院，沈阳110870）

【经济理论与应用】

大豆期货价格预测实证研究*

滕永平，周婷婷

（沈阳工业大学经济学院，沈阳110870）

在期货市场中，无论是企业套期保值来规避风险，还是投资者进行投机来获得利润，对期货价格进行合理预测都是特别重要的。选取2014－05－05—2015－08－31的大豆期货合约数据，运用统计学及计量经济学方法进行实证分析。利用ARMA模型进行预测，得出原数据与预测数据的对比图，证明基于ARMA模型的短期价格预测机制具有一定的准确性，可以为投资者提供参考。

大豆；期货价格；价格预测；ARMA模型；单位根检验；时间序列分析；白噪声检验

随着中国经济的发展，期货市场正在迅速崛起［1］，期货交易逐步进入人们的经济生活。虽然期货市场存在一定风险性，但通过时间序列模型研究可以提供投资参考信息［2］。时间序列模型在不同的时刻有不同的信息，可以更为准确地预测期货的价格走势。时间序列是依赖于时间的一组时间变量，构成该时序的单个序列值虽然具有不确定性，但整个序列的变化具有一定的规律性，可以用相应的数学模型进行描述，再通过对数学模型的研究与分析实现最小方差下的最优预测。

一、国内外研究现状

对期货价格的预测一直是国内外研究的重点。国外期货市场发展得较早，对期货市场的研究更加深入。Volkan Ediger等用ARIMA模型对土耳其2005—2020年间主要的能源需求进行了预测，得出ARIMA模型对能源类非平稳时间序列数据有较好拟合和预测效果的结论［3］。有些国外学者运用神经网络对价格进行预测，如Grudnitski G和Osburn L（1993）应用神经网络对S＆P指数和黄金期货价格进行预测［4］。Hossain等运用ARIMA模型对3种豆类的价格进行分析预测，通过相应对比分析发现这一模型对豆类价格具有较好的拟合和预测效果［5］。ARIMA模型与ARMA模型类似，只不过ARIMA模型中的I是对非平稳时间序列数据进行d次差分得到平稳数据后所建立的ARMA模型，差分次数d就是模型中的I值。

近年来，国内对期货价格预测的研究也逐渐发展起来。国内对价格预测的主要方法集中于两种：一是采用单一的模型进行检验与预测，二是运用两种或两种以上的模型进行比较或结合研究。杨娴等利用模型分析国际有色金属期货的市场风险。何晓光等基于ARMA-GARCH模型与VAR模型，对上海同业拆借市场的利率风险进行研究［6］。梅志娟（2010）对ARMA模型和GARCH模型进行对比分析，得出GARCH模型预测铜期货价格准确度更高的结论［7］。吴朝阳将ARMA模型与灰色模型结合起来对股指进行预测，并对灰色模型的缺陷进行改进，得出改进灰色模型和ARMA模型，使预测精度得到提高。闫冬（2012）基于ARMA-GARCH模型对上证指数进行短期的预测研究［8］。

本文采用大豆期货2014－05－05—2015－08－31的真实交易数据，利用计量经济学方法对ARMA模型进行实证分析，对大豆期货价格的时间序列数据进行整理从而建立模型；根据所建立的数学模型对大豆期货价格走势进行预测，得出ARMA模型对大豆期货价格的短期预测具有一定准确性的结论。总体来说，国外对ARMA模型的研究优于国内，但国内的研究数量也在逐步增加，有很大的发展潜力。

二、ARMA模型构建

ARMA模型由博克斯（Box）和詹金斯（Jenkins）创立，又称B-J方法。该模型又称自回归滑动平均模型（auto-regressive and moving average model），是研究时间序列的重要方法，由自回归模型（AR模型）与滑动平均模型（MA模型）为基础“混合”构成。AR模型又称自回归模型（auto regressivemodel），是一种线性预测，即已知N个数据，可由模型推出第N点前面或后面的数据（设推出P点），其本质类似插值，目的是为了增加有效数据。AR模型是由N点递推，而插值是由两点（或少数几点）去推导多点，所以AR模型要比插值方法效果更好［9］。MA模型即滑动平均模型（moving averagemodel），是模型参量法谱分析方法之一。ARMA模型的表达式为

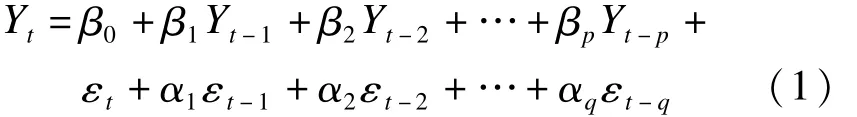
式中：p、q为模型的自回归阶数和移动平均阶数；ai、βi为不为0的待定系数；Yt为平稳、正态、零均值的时间序列；εt为独立误差项。

ARMA模型构建共包含5个步骤：

第一步，平稳性检验。时间序列模型必须是平稳的才可以进行ARMA建模。对一个非平稳的时间序列模型，需要先对它进行d次差分处理，直到其变为平稳的时间序列模型。

第二步，模型识别。根据时间序列数据样本自相关和偏自相关的值来确定模型中p和q的值，再根据最小信息准则来准确确定模型的阶数。

第三步，模型的参数估计。利用最小二乘法对模型进行参数检验，使其在统计上显著，具有统计意义。

第四步，模型的假设检验。模型选定之后对其进行白噪声检验，若均落在指定区域，说明没有需要再提取的信息。

第五步，预测。利用ARMA所建立的数学模型进行价格预测。

三、实证分析

1．数据选取

商品期货通常情况下流通量大，参与者基本都是价格的接受者，接近于完全竞争市场，有利于利用数据预测价格。在期货交易软件上，时间分为月、周、日、分钟。对选取数据而言，太短的周期具有突发性，不适合作为选取的对象；周期太长则会忽略掉中间的突变因素，同样不适合作为选取的对象。因此，本文选取2014－05－05—2015－08－31豆一期货的日收盘价作为研究数据。选择每个合约交割月份前2个月的价格，如a1507是2015年7月到期的豆一合约，则选择该合约交割前2个月即5、6月的合约，依此类推以便得到连续的期货价格。对节假日及个别缺失的数据进行剔除，使得数据更加真实有效。共选取330个数据，其中前309个作为研究对象，后21个作为预测数据的对比对象，以检测模型准确度。实证分析利用计量分析软件Eviews 7.2完成。

2．ADF检验

为了避免伪回归的产生，模型只有通过平稳性检验才有统计意义［10］。如果ADF检验中P＞0.05，则说明存在单位根，即数列具有不稳定性；若P＜0.05，则说明数据稳定［11］。原数列的单位根检验结果如表1所示，一阶差分后的序列单位根检验结果如表2所示。

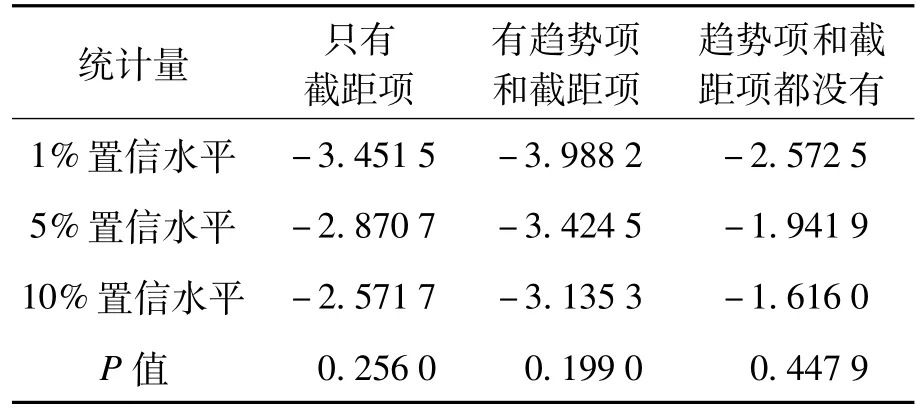
表1 差分前主要检测指标结果

表2 差分后主要检测指标结果

由表1、2的检验结果可知，原序列检验P＞ 0.05，说明原序列不稳定；一阶差分后的序列检验P＜0.05，说明一阶差分后的序列稳定，适合建立ARMA模型。

3．ARMA模型定阶

利用Eviews 7.2，得出一阶差分后序列自相关系数的3阶截尾、偏相关系数2阶截尾，初步断定模型为ARMA（2，3）；再根据AIC和SC最小信息准则来准确确定模型阶数［12］，选定ARMA（1，1），ARMA（1，2），ARMA（2，1），ARMA（2，2），ARMA（2，3）来进行比较，具体判定指标如表3所示。

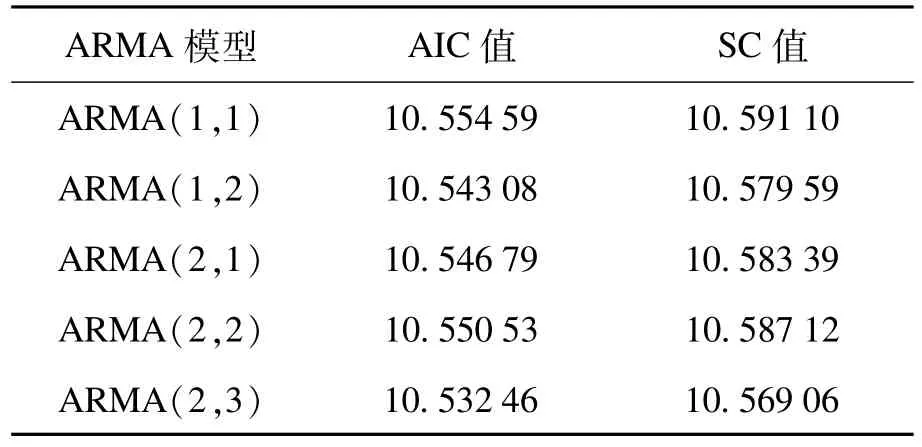
表3 ARM A模型相关判定指标

由表3可知，ARMA（2，3）模型的AIC值及SC值最小，根据最小信息准则该模型为最佳预测模型。利用OLS最小二乘法对模型进行检验，其中AR（1），MA（1）和MA（2）的P值明显较大，统计上不显著。剔除后再运用最小二乘法进行线性回归，得出AR（2）和MA（3）的P＜0.05，统计上显著，可以建立模型，即

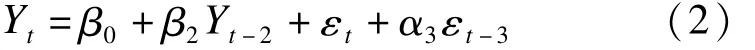
4．白噪声检验

模型选定之后需要进行白噪声检验，如果残差序列的自相关均落入选定区域，则说明序列是白噪声序列，再没有需要提取的信息了；反之则不是残差序列，需要进一步改进［13］。残差检验结果如表4所示。

表4 残差检验结果

由表4可知，残差序列的自相关与偏相关均在选定区域内，且Q统计量的P值从3阶开始都大于0.05，说明已建模型的随机误差相是白噪声序列，可以用该模型进行价格预测。对模型进行OLS回归，得出各项系数为c＝－1.296 0，AR（2）＝－0.122 9，MA（3）＝－0.144 6，则模型表达式为

四、预测与检验

利用式（3）进行价格预测，得到真实期货价格与预测期货价格对比，如图1所示。

由图1可知，预测价格与真实价格整体走势大致相同，说明预测结果具有一定的准确性。选出前5日大豆期货价格预测值进行误差检验，结果如表5所示。

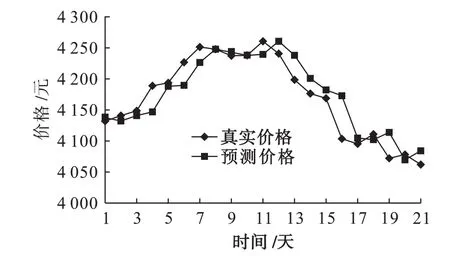
图1 原数据与预测数据对比

如表5所示，2015－08－03—2015－08－07的期货预测价格误差率都很小，说明预测值比较接近真实值，此预测模型具有一定的有效性，能够为投资者提供投资参考。

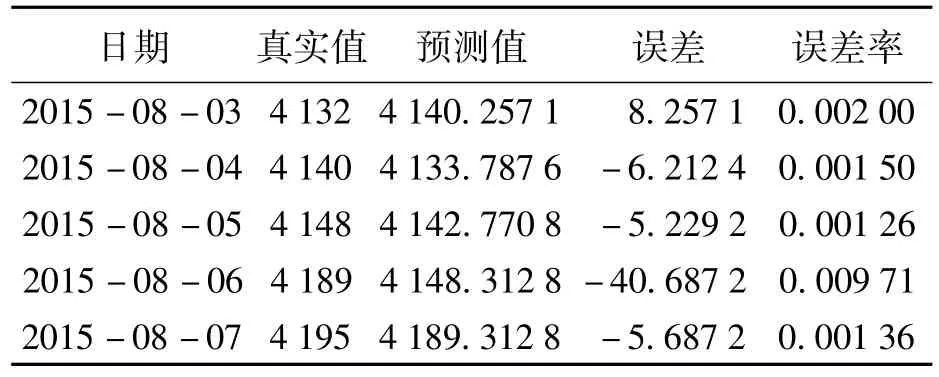
表5 部分预测值误差率 元

五、结论与启示

本文利用ARMA模型对2014－05－05—2015－08－31的大豆期货时间序列数据进行实证分析，并进行模型预测效果检验。大豆期货的时间序列数据是非平稳性数据，需要进行差分平稳化处理使其具有稳定性，再利用自相关与偏自相关系数进行模型定阶，最后进行建模预测。预测结果表明，通过历史时间序列数据对大豆期货价格进行ARMA建模，所得预测价格与真实价格走势大致相同，虽然有一定的误差，但误差率较小。该结果与已有研究相符，说明运用ARMA模型对大豆期货价格进行短期预测具有一定的准确性，对进一步研究期货价格预测问题具有一定辅助作用。

本文得出的预测价格与真实价格有一定误差，为了使结果更有利于投资者，根据本文研究可得到如下启示：

（1）综合预测。价格信息具有多变性，结合技术面与基本面信息同时进行预测，可以降低误差率，更有利于投资者。也可以在进行期货投资的同时进行期权投资，这一方面可以在一定程度上规避金融市场风险性，另一方面可以从中获得额外收益。

（2）由于ARMA模型是线性预测，为了使预测更有效，可以将线性预测与非线性预测结合起来，这将是下一步研究的重点。

（3）鼓励更多的投资者进入期货市场。更多的投资者进入期货市场，会使市场更具竞争力，使价格的形成更具市场性。

［1］王一如，赵庆.大连期货市场发展问题及对策研究［J］.现代商贸工业，2015（20）：127－129.

［2］马保忠，甄博倩.基于时间序列分析的黄金期货价格预测模型的实证分析［J］.商，2015（7）：152－155.

［3］Volkan E，Sertac A.ARIMA forecasting of primary energy demand by fuel in Turkey［J］.Energy Policy，2007（35）：1701－1708.

［4］Grudnitski G，Osburn L.Forecasting S＆P and gold futures prices：an application of neural networks［J］. Journal of Futures Markets，1993，13（6）：631－643.

［5］Hossain M Z，Samad Q A，A li M Z.ARIMA model and forecasting w ith three types of pulse prices in Bangladesh：a case study［J］.International Journal of Social Econom ics，2006，33（4）：344－353.

［6］李洛源.基于VAR方法的上海银行间同业拆借利率风险度量［J］.经营管理者，2016（1）：26－27.

［7］梅志娟.ARMA-GARCH模型的期货价格预测比较研究［J］.经济研究导刊，2010，34（1）：73－74.

［8］闫冬.基于ARMA-GARCH模型的上证指数短期预测研究［J］.重庆理工大学学报（社会科学版），2012（10）：36－39.

［9］吴少华.县域城市天然气需求预测模型及其不均衡性对策研究［D］.镇江：江苏大学，2012.

［10］陈昭.时序非平稳性ADF检验法的理论与应用［J］.广州大学学报（自然科学版），2008（5）：5－10.

［11］王博.基于ARMA-GARCH模型的上证指数实证分析［J］.科学技术与工程，2012（5）：1219－1221，1226.

［12］潘贵豪，胡乃联，刘焕中，等.基于ARMA-GARCH模型的黄金价格实证分析［J］.黄金，2010（1）：5－8.

［13］李战江，张昊，孙鹏哲，等.基于ARIMA模型的沪深300股指期货价格预测研究［J］.鲁东大学学报（自然科学版），2013（1）：22－24.

Em pirical study on price prediction of soybean futures

TENG Yong-ping，ZHOU Ting-ting
（School of Econom ics，Shenyang University of Technology，Shenyang 110870，China）

In the futuresmarket，the proper prediction of futures price is especially important whether for the enterprises to avoid risk by hedging，or for the investors to acquire profit by speculating.The data of soybean futures contract from May 5，2014 to August31，2015 are selected to conduct empirical analysis by applying statistic and econometric methods.Prediction is produced by applying ARMA model，and comparative chart of raw data and predicting data is acquired.This study proves that the forecasting mechanism of short-term price based on ARMA model has certain accuracy，and can provide reference for investors.

soybean；futures price；price prediction；ARMA model；unit root test；time series analysis；white noise test

F 831.5

：A

：1674－0823（2017）04－0331－04

10.7688／j.issn.1674－0823.2017.04.07

（责任编辑：郭晓亮）

2016－07－06

辽宁省财政科研基金项目（15B03）。

滕永平（1962－），男，山东荣成人，教授，主要从事金融市场学等方面的研究。

*本文已于2016－11－29 09∶09在中国知网优先数字出版。网络出版地址：http：∥www.cnki.net／kcms／detail／21.1558.C. 20161129.0909.014.htm l