高中数学不等式易错题型及解题技巧
2017-09-03戴安妮
戴安妮
(江苏省淮阴中学高二8班,江苏 潍安 223000)
高中数学不等式易错题型及解题技巧
戴安妮
(江苏省淮阴中学高二8班,江苏 潍安 223000)
高中阶段是为高考打基础的三年,而不等式在高考的数学科目中占据了重要的地位.在高考的考点中,就分布着不等关系与不等式、一元二次不等式及其解法、简单的线性规划、基本不等关系、不等式的综合应用和不等式的证明这六个考点.在它们之中,万变不离其宗的就是不等式.但是我们高中生在不等式方面却很难拿分,通过调查,我发现同学们面临着不会运用数形结合方法,不会灵活运用均值不等式等问题.本文通过解析高中数学不等式易错题型和解题技巧,来帮助同学梳理不等式的学习方法.
高中数学,不等式,定义域,数形结合,均值不等式
不等式在高考中占据重要地位,很多大题中也融合了不等式思想,但我们的同学往往因为不等式解题思想不明了,解题脉络不清晰而在求解不等式步骤中阻滞不前,从而放弃整道大题的分值.也有同学因此对不等式望而却步,认为太复杂了,自己肯定学不会,干脆放弃不等式方面的学习.
但这样会直接导致一些容易拿的分的无意义流失.其实,结合我自身的经验,只要理清方法,抓住易错题型和解题技巧,不等式并不难.
一、忽视函数定义域或取值范围
在解题时,同学常犯的一个典型错误就是忽略题干给出的函数的定义域,变量的取值范围,或者忘记函数本身的性质,忽略函数本身有意义时的存在条件,从而导致做题出现偏差.
因此,我们解题时一定要牢记几个基本函数的定义域:分数的分母不能为零;偶次方根底数大于等于零;零的零次方无意义,若有x0,则x不等于零;对数函数的底数大于零且不等于1,真数大于0;指数函数的底数大于零且不等于1.
以上这些内容一般都隐含在数学题之中,通常都是由于每个小点知识自身具有的一些性质,这是我们高中生解题时必须要考虑到的问题.这些问题属于解题之中的一些细枝末节,但正是这些细枝末节,可以检查出我们高中生对于数学知识的理解以及应用程度.因此,我们高中生在解函数与不等式相结合的数学题时,除了要注重对题干进行透彻分析之外,还要重视函数自身定义域以及取值范围.
二、不会运用数形结合思想
很多同学在面对看似无法运算的题型时,感到十分棘手,不知道从何下手.我之前也出现这种情况,但随着做题量的增多,我发现这种题型可以运用数形结合思想.概括来讲,数形结合思想解题基本运用了“由形化数”“由数化形”“数形转换”这三种解题思路和方法.而转换数与形也有三条基本的途径:①建立坐标系,化静为动,更加直观;②转化,换角度思考,不在一条路上钻牛角尖;③构造,在本来没有的基础上构造函数或者几何图形.
通常来说,在不等式中,数形结合思想通常运用在求参数的取值范围或者解不等式上,这样可以使得原本较为抽象的知识具体化,并且在解题时可以非常直观地获得答案,降低解题的错误率.在面对这两类问题时,如果同学感到没有头绪,不妨运用数形结合思想.
答案 (-∞,0].
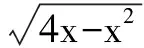
三、不会运用均值不等式
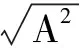
它具有的注意点:
(1)求最值的条件“一正二定三相等”
一正:A、B必须都是正数;
二定:积定和最小、和定积最大;
三相等:当且仅当A、B相等时,等式成立,
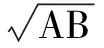
(2)当两个正数的积为定值时,可以求它们的和的最小值,当两个正数的和为定值时,可以求它们的积的最小值,所谓“积定和最小,和定积最大”
下面来解析具体题型:
1.求值域
技巧一:凑项
例1 已知x<5/4,求函数y=(4x-2)+1/(4x-5)的最大值.
解 因4x-5<0,所以首先要“变号”,又(4x-2)+1/(4x-5)不是常数,所以对(4x-2)要进行拆、凑项.
因为x<5/4,所以5-4x>0,所以y=(4x-2)+1/(4x-5)=-[(5-4x)+1/(5-4x)]+3≤-2+3=1
当且仅当5-4x=1/(5-4x),即x=1时,上述等号成立,故当x=1时,y最大值=1
评注 本题需要调整项的符号,又要配项的系数,使其积为定值.
技巧二:减系数
例2 当0 解析:由0 当2x=8-2x,即x=2时取等号. 当x=2时,y=x(8-2x)的最大值为8. 技巧三:换元 在面对看似无法运算的不等式时,可先换元,将t带入,化简原式之后分离求值. 在针对函数求值域这一类问题来看,我们可以通常采用三种方法来解题,凑项、减系数以及换元这三种方法都是我们常用的方法.其中凑项以及减系数这两种方法是我们在解题期间常考虑到的两种方法,但其应用范围有限,有一些题型应用这两种方法不一定能解出来.然而,换元这一方法使用的范围较广,我们高中生在没有解题思路时可以直接这种方法来进行解题,进而寻找解题思路. 2.求最值 在利用均值不等式求最值时通常有以下几种情况:求几个正数和的最小值,求几个正数积的最大值,根据均值不等式判断最值符号是否成立,带条件求最值. 例3 若x,y∈R+,求f(x)=x+(4/x)(0 解法一 (数形结合)由函数f(x)=ax+(b/x)(a,b>0)图象及性质知,当x∈(0,1]时,函数f(x)=x+4/x是减函数. 证明 任取x1,x2∈(0,1]且0 解法二 (导数法)由f(x)=x+4/x得f’(x)=1-4/x2,当x属于(0,1]时f’(x)=1-4/x2<0 则函数f(x)=x+4/x在(0,1]上是减函数,故当x=1时,f(x)=x+4/x在(0,1]上有最小值5 解法三 (拆分法)f(x)=x+4/x(0 当且仅当x=1时“=”成立,故此函数最小值是5 这三种解法都可以得到正确的答案,对于同一题型,我们高中生可以分别从这三个不同的角度来进行解题.这三种解法分别从数形结合、导数法以及拆分法三个角度进行解题.从这三个解题方法可以看出,导数法以及数形结合这两种方法通常对于我们高中生来说在解题期间比较常用,而拆分法这种形式来看,其方法固然简单,但是我们在拆分时不容易想到将原来的算式拆分成哪几项,如果拆分的不对,很容易出现错误.因此,在求解此类问题,要在确保基本原则的同时,灵活选用方法. 不等式是高中数学学习的重难点,也是我们高考考生拿分的必备基础知识.我们在面对不等式时,要保持思维的冷静和缜密,不要自乱阵脚.梳理出所属题型和所要用的解题方法和思路,然后顺藤摸瓜,一步步地理清脉络,逐步解开题.同时,在读题时一定要细心冷静,不能忽略题干中的关键信息,一旦忽略就可能让有把握的题做错,从而让分数无意义流失.不等式的掌握是一个漫长又需要细心和耐心的过程,同学们在学习时不能气馁,一旦掌握就能举一反三,灵活运用. [1]张惠淑.高中数学不等式高考试题分析与教学策略研究[D].天津师范大学,2012. [2]钱煜.基于高考试题的高中数学不等式教学研究[D].天津师范大学,2014. [责任编辑:杨惠民] 2017-05-01 戴安妮(2000.7-),女,江苏淮安人,高中学生. G632 B 1008-0333(2017)19-0048-02