温度及含水率对落叶松和白桦动态黏弹性的定量分析1)
2017-09-03杨叶丽蔡英春付宗营赵景尧
杨叶丽 蔡英春 付宗营 赵景尧
(东北林业大学,哈尔滨,150040)
温度及含水率对落叶松和白桦动态黏弹性的定量分析1)
杨叶丽 蔡英春 付宗营 赵景尧
(东北林业大学,哈尔滨,150040)
利用动态热机械分析仪检测了落叶松和白桦试材在不同含水率下的玻璃化转变温度(tg),研究了二者的关系及不同初含水率下储能模量随温度变化的规律。结果表明:落叶松和白桦试材玻璃化转变温度均随含水率升高而线性降低,表征二者关系的两个线性方程之决定系数分别高达0.996 46与0.979 86;含水率每增大1%所引起的玻璃化转变温度的降低值,落叶松为6.71 ℃,大于白桦的6.64 ℃。落叶松和白桦的储能模量均随其温度、初含水率的升高而减小。落叶松的储能模量以约70 MPa/℃的平均幅度随温度的升高近似呈线性减小趋势。白桦储能模量在初含水率6%~13%时,约以146.9 MPa/℃的平均幅度随温度的升高呈近似线性减小趋势;初含水率在15%~22%,随温度的上升产生了较为明显的突变点,在100 ℃左右急剧减小。所得落叶松和桦木储能模量与温度及含水率关系的两个数学表达式的决定系数分别达到0.910 43和0.886 54。
变定处理;木材含水率;玻璃化转变温度;储能模量
木材作为天然高分子材料,具有黏弹性特征,在流变学上体现为储能模量、损耗模量、损耗因子等。其中储能模量的大小体现材料的弹性特征,损耗模量及损耗角正切的大小体现材料的阻尼特性;黏弹性特征中损耗因子峰值所对应的温度为材料的玻璃化转变温度[1],在该温度以下时,木材的弹性较强;在该温度以上时,木材的弹性显著下降[2]。所以该温度亦称谓软化点。20世纪70年代以来,国内外研究人员一直致力于研究木材的黏弹性特征,比较分析了不同情况下木材的动态黏弹性,取得了诸多成果。蒋佳荔[3-9]定性分析了-120~40 ℃下杉木动态黏弹性与含水率的依存性,研究发现该温度范围内,杉木储能模量和玻璃化温度均随含水率的升高而降低。E. Obataya、Y. Furuta et al.[10-11]日本学者对化学改性木材以及扁柏的动态黏弹特性进行了研究。Beckman[12]利用动态热机械分析仪器,研究了樟子松弦向和径向的动态机械特性。徐信武[13]研究了不同含水率速生杨木的弹性和黏性转变温度,为速生杨木的压缩强化、尺寸稳定化处理提供了参考依据。尽管目前对于木材的动态黏弹性特征已经有较多的研究成果,但由于木材树种之间的差异及实验条件设置的不同,无法将结果推广到各个树种,且缺乏定量研究。
桦木,通直的适用于家具用材,弯曲的可横截成树盘、制成高附加值的工艺品等;落叶松小径木适用于木结构建筑用材(日式木建筑立柱常为含髓心方材)。家具用材的弯曲加工需要软化、定型处理;树盘干燥开裂的抑制,需要在接近纤维饱和点时软化处理以松弛应力;含髓心方材干燥表裂的抑制,需在前期进行软化、变定处理。桦木和落叶松不同含水率时玻璃化转变温度、含水率和温度对储能模量影响规律的把握,可为前述处理工艺的优化提供依据。本研究以白桦和落叶松为对象,测定了其在30~150 ℃温度下不同平衡含水率时的储能模量和损耗因子,定量地解析了白桦与落叶松不同含水率、温度下的储能模量以及不同含水率时的玻璃化转变温度。以期为前述软化和定型、软化松弛应力、软化变定等处理工艺优化提供理论依据,为需密实化处理的杨木等软质木材的相关研究提供借鉴。
1 材料与方法
1.1 材料与仪器设备
试件:取自白桦和落叶松板材,无节子和缺陷、尺寸为35 mm(长)×10 mm(宽)×2.5 mm(厚)。主要仪器设备:GDS-100恒温恒湿干燥箱,温度范围-10~100 ℃,波动度±0.5 ℃,湿度范围35%~98%,波动度±3 ℃;DHG-9070A型电热恒温鼓风干燥箱,上海-恒科技有限公司;电子天平,LT210/0.01 g;美国TA-Q800 DMA动态热机械分析仪,频率范围0.01~200 Hz、温度范围-150~600 ℃。
1.2 方法
试件水分的平衡处理:采用恒温恒湿箱对试件水分进行平衡处理,通过调节箱体内干、湿球温度,调制5个不同的恒温恒湿环境,将试件分别置于其中进行吸湿或解吸。当试件在24 h内质量不变时,可认为试件含水率达到平衡状态,称质量并计算其平衡含水率。5个温、湿度环境及其所对应的试件实际平衡含水率如表1所示。
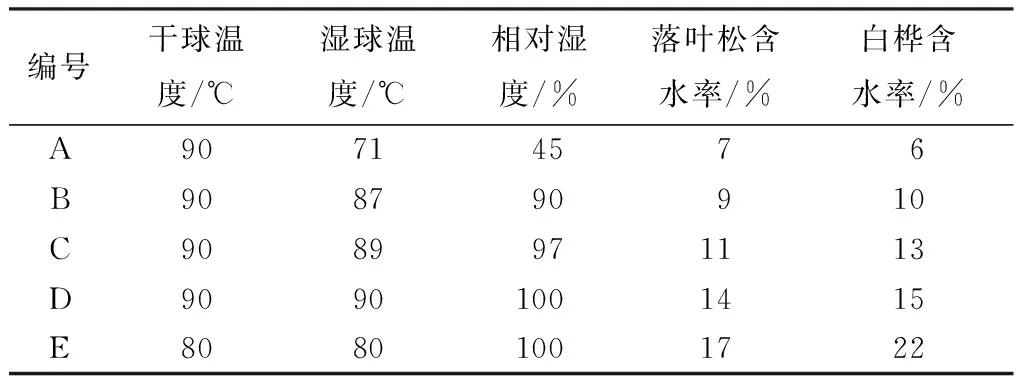
表1 平衡处理环境条件及试件平衡含水率
动态黏弹性测定:动态热机械分析仪采用三点弯曲形变模式,测量表1所列试件的储能模量、损耗因子,由损耗因子确定玻璃化转变温度。测定温度范围:30~150 ℃,设定频率为1 Hz,升温速率为5 ℃/min。
试件上述测定过程含水率变化检测:为研究确定动态黏弹性与含水率的关系,需确定试件在动态黏弹性测定过程含水率的变化规律。由于分析仪内试件质量、试件环境湿度不能检测,所以,本研究将平衡处理后不同含水率试件(表1)置于与DMA测试箱体容量、通气孔尺寸一致的金属容器中,使用电热干燥箱按1.2中所述DMA测试时的温度范围和升温速率加热、称质量,间接实现试件在动态黏弹性测定过程含水率变化的检测。
2 结果与分析
2.1 玻璃化转变温度与含水率的关系
5组不同初含水率(MC)白桦和落叶松试件损耗因子随温度(t)的变化如图1、图2所示,峰值所对应的温度即为玻璃化转变温度(tg),图中对不同初始含水率状态下对应的tg数据进行了标注。
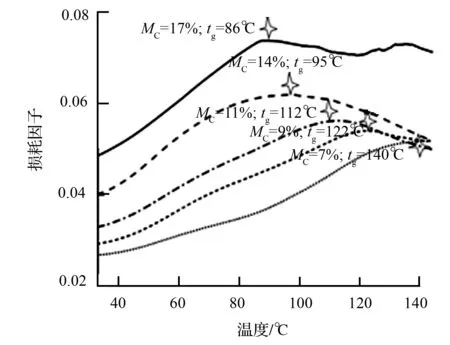
图1 落叶松损耗因子与温度、初含水率关系
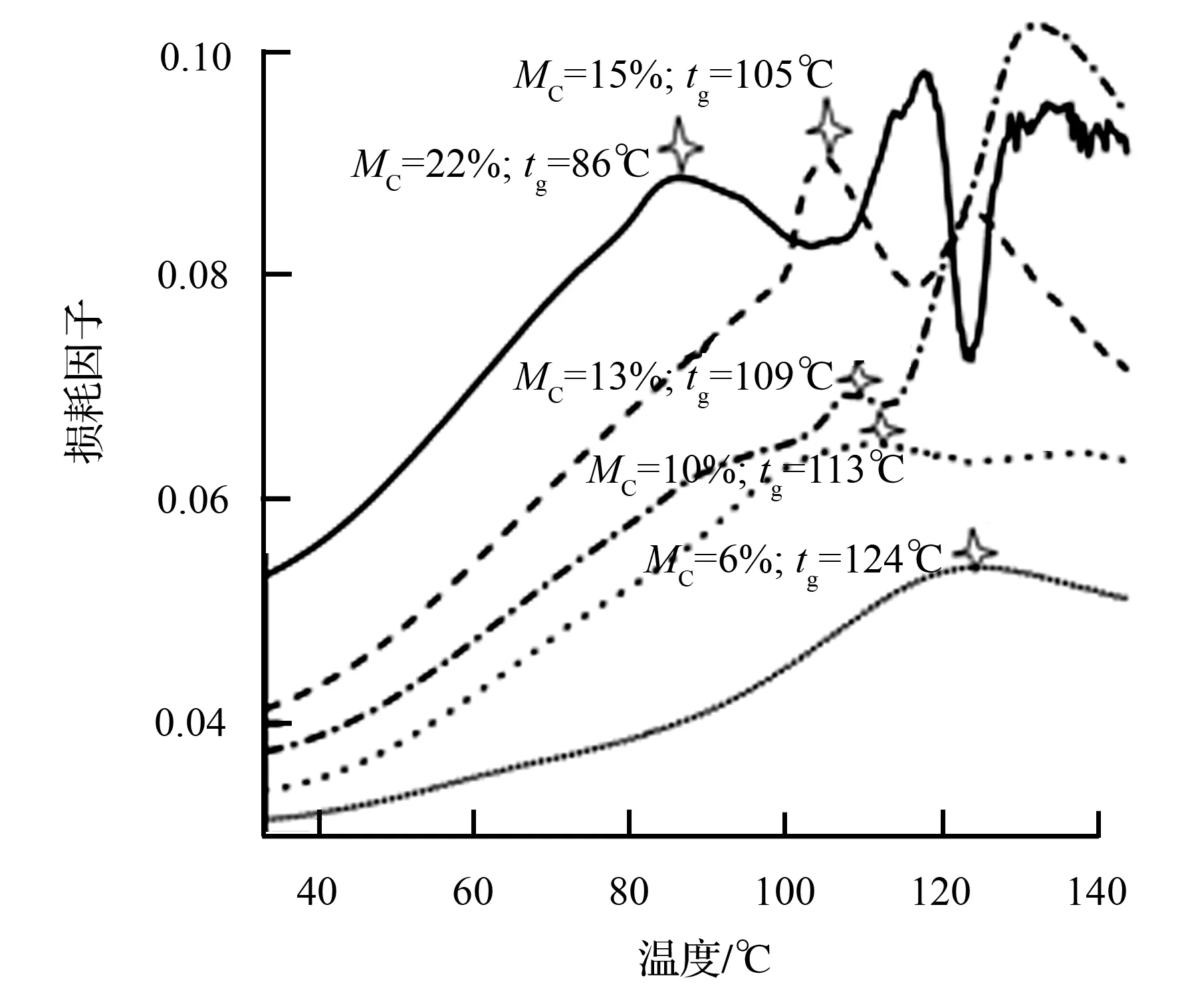
图2 白桦损耗因子与温度、初含水率关系
不同初含水率试件在不同含水率时的玻璃化转变温度如表2所示。从图1、图2及表2可以看出,落叶松与白桦的玻璃化转变温度均随含水率的升高而降低。为定量描述落叶松与白桦玻璃化转变温度随含水率变化的关系,对表2表述的两种树种的玻璃化转变温度与含水率的关系进行线性回归分析,如图3、图4所示,得到拟合方程(1)、(2)。
落叶松:
tg=-6.709 59MC+140.253 79(0≤MC≤8%;R2=0.996 46)。
(1)
白桦:
tg=-6.643 87MC+141.017 97(2.5%≤MC≤8%;R2=0.979 86)。
(2)
由式(1)、式(2)可知,落叶松与白桦的玻璃化转变温度随含水率的上升均呈线性下降趋势,方程的决定系数分别高达0.996 46与0.979 86,表明由该二式可分别较准确地计算两树种木材不同含水率时的玻璃化转变温度。由表2可知,落叶松的玻璃化转变温度,在0~8%的含水率变化范围内从140 ℃降低到86 ℃,含水率每增大1%平均下降6.71 ℃;白桦的玻璃化转变温度,在2.3%~8.0%的含水率变化范围内从124 ℃降低到86 ℃,含水率每增大1%平均下降6.64 ℃。玻璃化转变温度随含水率增大而下降的原因是木材中水分含量增加,所以从外界环境中获取较少的热量就可以使运动单元克服位垒以一定方式运动[7]。此外,木材含水率的增大,单位体积内纤维素和木质素分子的数目减少,摩擦力降低,分子间的结合力减弱[14]194也是其玻璃化转变温度下降的原因。
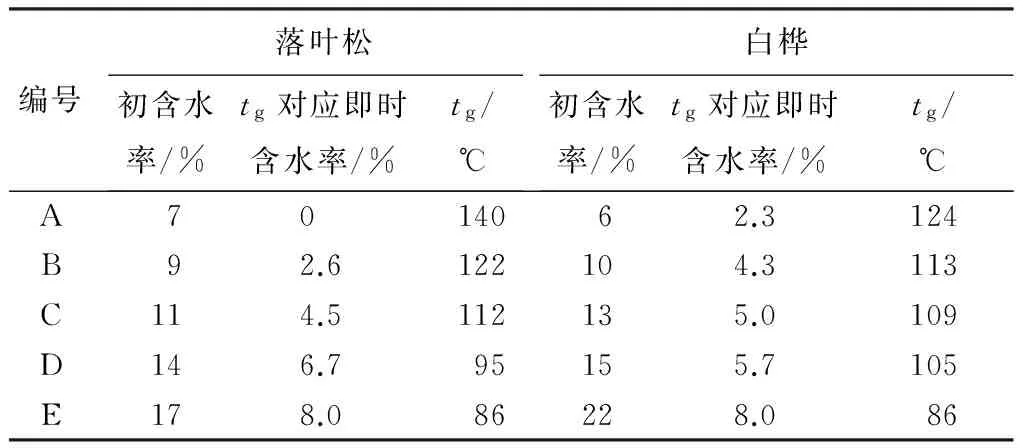
表2 不同含水率处理材的玻璃化转变温度
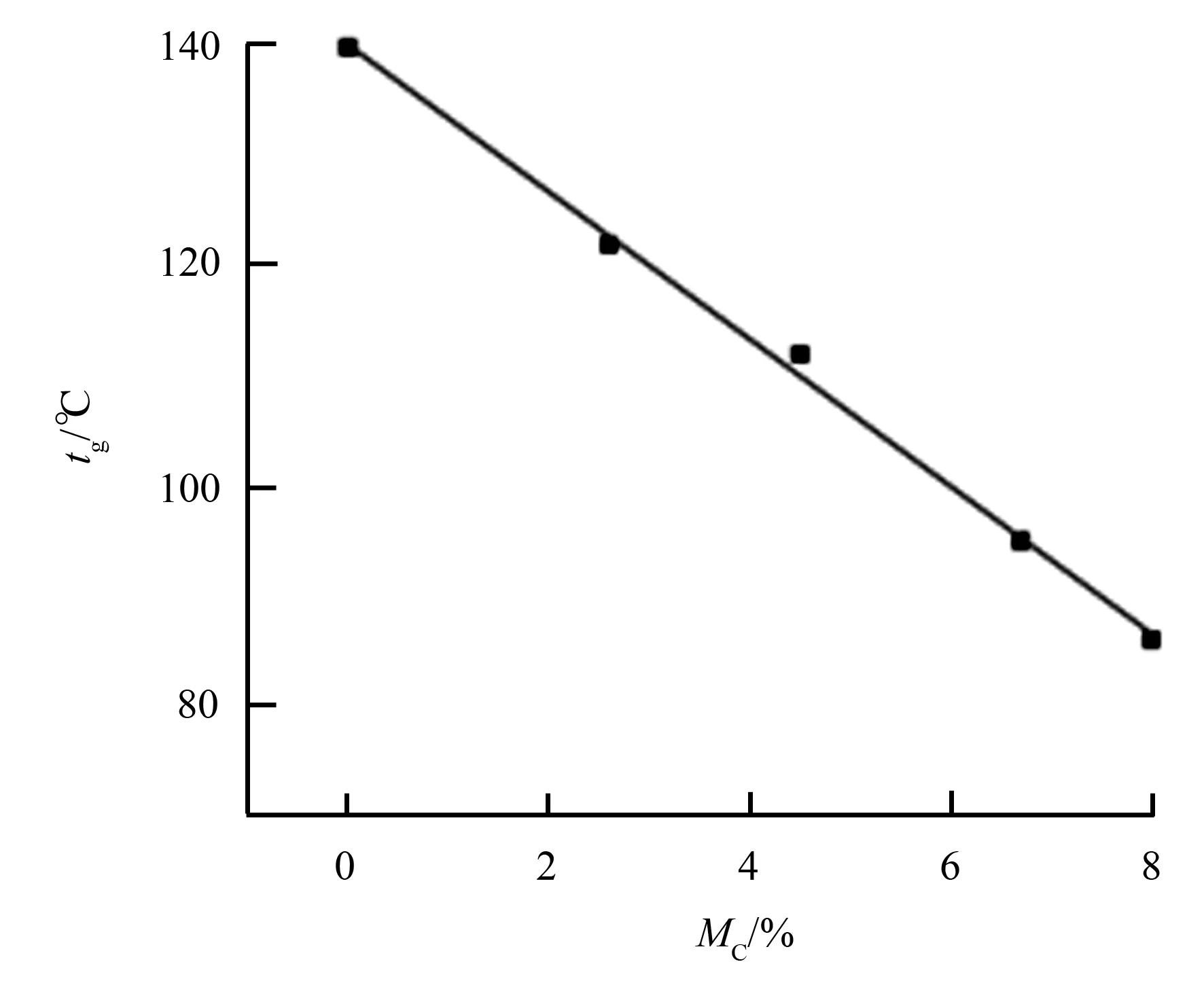
图3 落叶松玻璃化转变温度与含水率关系
2.2 储能模量与温度、初含水率关系
图5、图6分别示出了不同初含水率(试件在动态黏弹性检测前的含水率)落叶松、白桦试件储能模量(E′)与温度的关系。
对图5、图6的原始数据进行回归分析,所得三元方程(储能模量与温度及含水率关系的数学表达式)如式(3)、(4)所示。
落叶松:
E′=71.511 7t-1 291.710 22MC+42 526.864 01 (7%≤MC≤17%;R2=0.910 43);
(3)
白桦:
E′=186.233 5t-919.448 75MC+54 087.825 64 (6%≤MC≤22%;R2=0.886 54)。
(4)
式中:E′为试件的储能模量(MPa);t为试件温度(℃);MC为试件的初始含水率(%)。
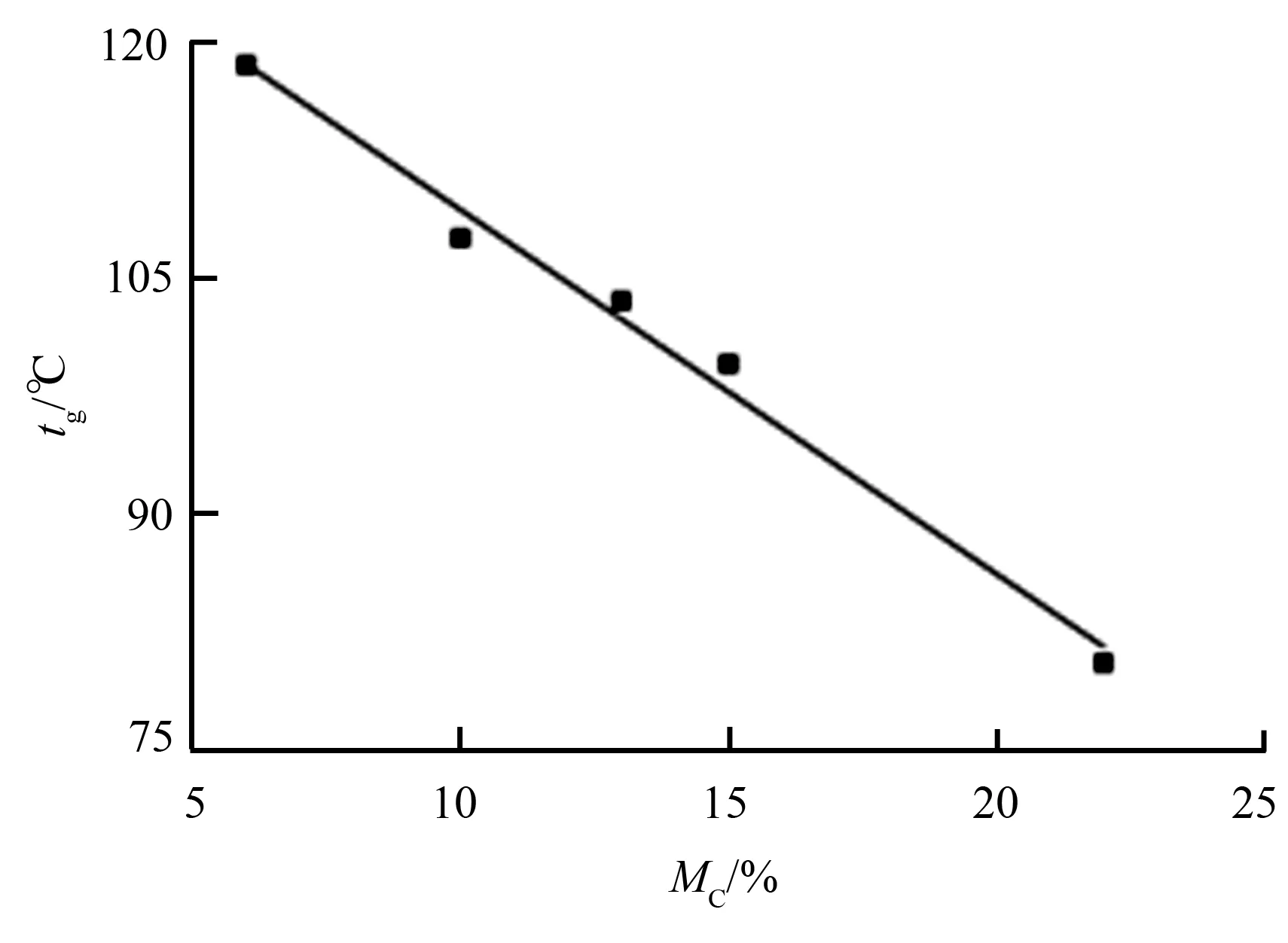
图4 白桦玻璃化转变温度与含水率关系
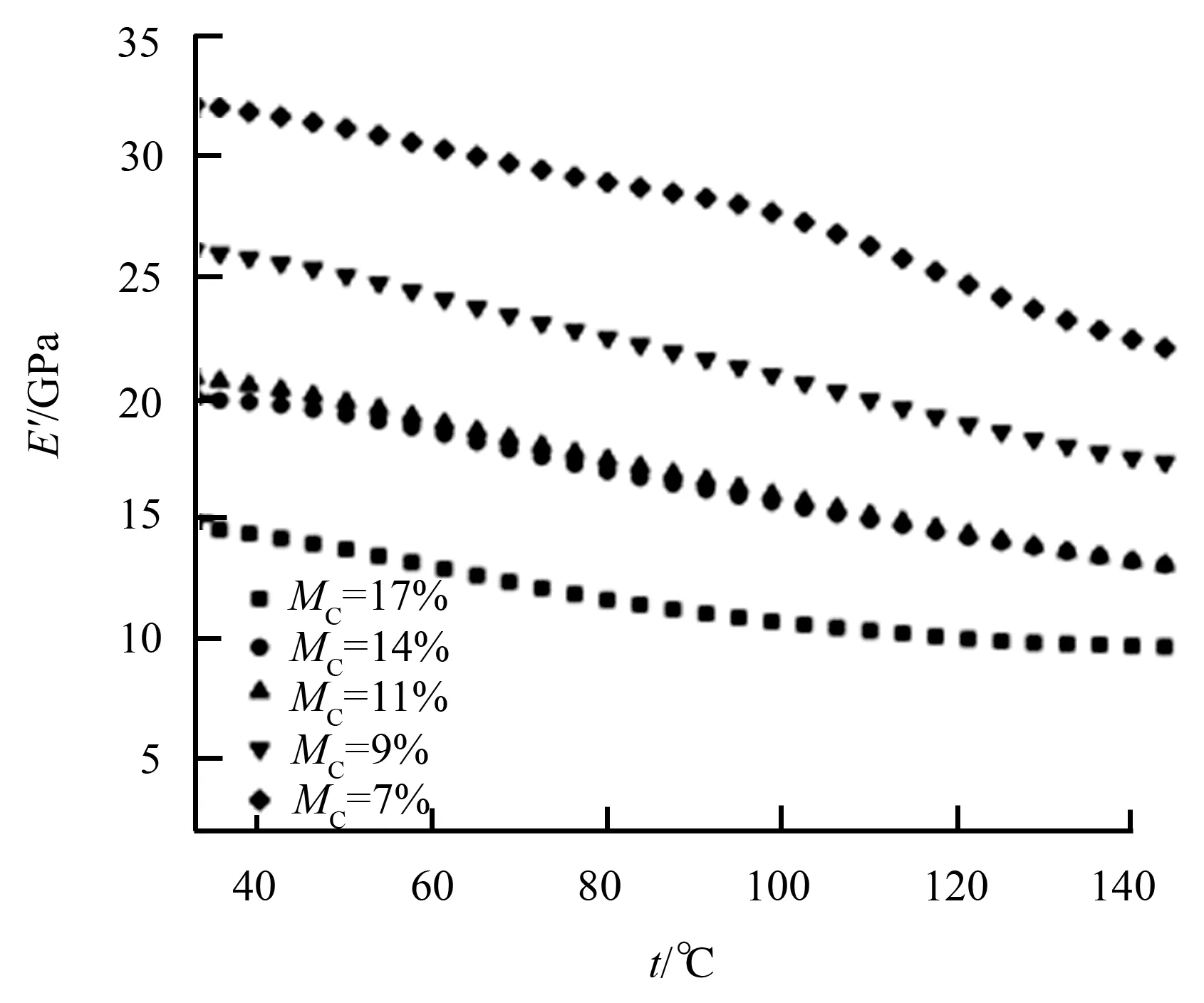
图5 落叶松储能模量与温度、初含水率关系
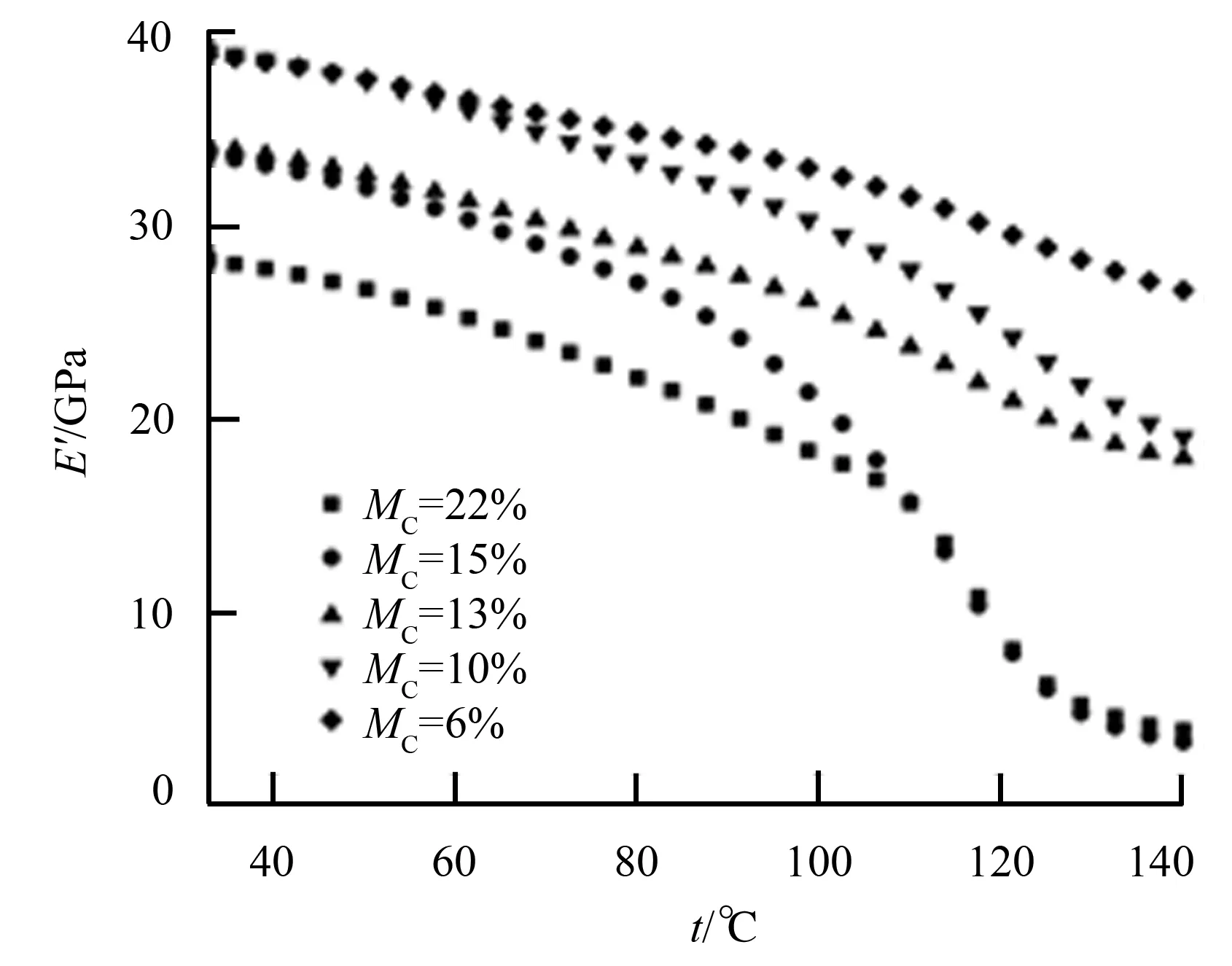
图6 白桦储能模量与温度、初含水率关系
由图5、图6和式(3)、式(4)可知,白桦和落叶松的储能模量均随着其温度、初含水率的升高而减小,但不同种木材在相同含水率范围内或同种木材在不同含水率范围内减小程度不同。图5的数据表明,落叶松的储能模量以约70 MPa/℃的平均幅度随温度的升高近似呈线性减小趋势。由图6可知,初含水率在6%~13%,白桦储能模量约以146.9 MPa/℃的平均幅度随温度的上升呈近似线性减小趋势;初含水率在15%~22%,储能模量随温度的上升产生了较为明显的突变点,在100 ℃左右急剧减小。
式(3)、式(4)的决定系数分别达到0.910 43和0.886 54,表明在一定初含水率范围内,可根据该两式由初含水率分别较准确地确定落叶松及白桦试材不同温度下的储能模量。
温度对储能模量影响的主要原因为,温度升高,细胞壁物质分子运动加剧,微纤丝间松动增加,分子间摩擦力下降[14]195,因而导致木材储能模量减小;初含水率对储能模量影响的主要原因,与2.1节所述木材含水率对玻璃化转变温度的影响原因一致。
3 结论
落叶松和白桦试材玻璃化转变温度均随含水率升高而线性降低。前者在在0~8%的含水率范围内,后者在2.3%~8.0%的含水率范围内表征二者关系的两个线性方程之决定系数,分别高达0.996 46与0.979 86,表明由两式可较准确地计算两树种木材不同含水率时的玻璃化转变温度;含水率每增大1%所引起的玻璃化转变温度的降低值,落叶松为6.71 ℃,大于白桦的6.64 ℃。
落叶松和白桦的储能模量均随着其温度、初含水率的升高而减小。落叶松的储能模量以约70 MPa/℃的平均幅度随温度的升高近似呈线性减小趋势。白桦储能模量在初含水率6%~13%时,约以146.9 MPa/℃的平均幅度随温度的上升呈近似线性减小趋势;在初含水率15%~22%,随温度的上升产生了较为明显的突变点,在100 ℃左右急剧减小。
所得落叶松和白桦储能模量与温度及初含水率关系的两个数学表达式的决定系数分别达到0.910 43和0.886 54,表明在一定初含水率范围内,可根据两式由初含水率分别较准确地确定两树种试材不同温度下储能摸量。
[1] 李坚.木素的玻璃态转变与热磨法制浆工艺[J].林业科技,1986(1):38-39.
[2] 王雁冰,黄志雄,张联盟.DMA在高分子材料研究中的应用[J].国外建材科技,2004,25(2):25-27.
[3] 蒋佳荔,吕建雄.杉木动态黏弹行为的时温等效性[J].林业科学,2012,48(2):124-128.
[4] 蒋佳荔,吕建雄.干燥处理木材动态黏弹性的含水率依存性[J].林业科学,2008,44(9):118-124.
[5] JIANG J L, LU J X, HUANG R F, et al. Effects of time and temperature on the viscoelastic properties of Chinese fir wood[J]. Drying Technology,2009,27(11):1229-1234.
[6] JIANG J L, LU J X, ZHAO Y K, et al. Influence of frequency on wood viscoelasticity under two types of heating conditions[J]. Drying Technology,2009,28(6):823-829.
[7] 蒋佳荔.干燥处理材的动态黏弹性研究[D].北京:中国林业科学研究院,2006.
[8] 蒋佳荔,吕建雄.木材动态黏弹性的湿热耦合效应[J].林业科学,2014,50(12):101-108.
[9] JIANG J L, LU J X. Dynamic viscoelasticity of wood after various drying processes[J]. Drying Technology,2007,26(5):537-543.
[10] FURUTA Y, OKUYAMA T, KOJIRO K, et al. Temperature dependence of the dynamic viscoelasticity of bases of Japanese cypress branches and the trunk close to the branches saturated with water[J]. Journal of Wood Science,2014,60(4):249-254.
[11] OBATAYA E, FURUTA Y, GRIL J. Dynamic viscoelastic properties of wood acetylated with acetic anhydride solution of glucose pentaacetate[J]. Journal of Wood Science,2003,49(2):152-157.
[12] BACKMAN A C, LINDBERG K A. Differences in wood material responses for radial and tangential direction as measured by dynamic mechanical thermal analysis[J]. Journal of Materials Science,2001,36(15):3777-3783.
[13] 韩书广,那斌,罗婉珺,等.不同含水率速生杨木DMA图谱分析及应用[J].东北林业大学学报,2011,39(9):69-70,96.
[14] 徐明.木材学[M].北京:中国林业出版社,2006:194-195.
Effects of Temperature and Moisture Content on Dynamic Viscoelasticity of Larch and Birch//
Yang Yeli, Cai Yingchun, Fu Zongying, Zhao Jingyao
(Northeast Forestry University, Harbin 150040, P. R. China)
//Journal of Northeast Forestry University,2017,45(8):66-69.
Dynamic mechanical analysis (DMA) of the White Birch and Larch were performed using a TAQ800 analyzer. The effect of moisture content on the glass transition temperature and the effect of temperature and initial moisture content on the storage modulus for White Birch and Larch were acquired. The glass transition temperature of larch and birch decreased linearly with the increase of moisture content, and the coefficient of determination of the two linear equations were 0.996 46 and 0.979 86, respectively. Each percent of moisture content increase cause the reduction of glass transition temperature for 6.71 ℃ on larch which is greater than that of birch for 6.64 ℃. The storage modulus of White Birch and Larch decreased with the increase of temperature and initial moisture content. The storage modulus of larch decreased approximately linearly with the increase of temperature at the average amplitude of about 70 MPa/℃. As for larch, the storage modulus was decreased with the decreasing temperature at the average amplitude of about 146.9 MPa/℃ when the initial moisture content was between 6% and 13%, and decreased drastically at 100 ℃, when the initial water content was between 15% and 22%. The correlation coefficients of the two mathematical expressions of the relationship of the storage modulus including temperature and water content of larch and birch were 0.910 43 and 0.886 54, respectively.
Drying set; Moisture content of wood; Glass transition temperature; Storage modulus
1)国家自然科学基金项目(31270595)。
杨叶丽,女,1991年2月生,东北林业大学材料科学与工程学院,硕士研究生。E-mail:631075611@qq.com。
蔡英春,东北林业大学材料科学与工程学院,教授。E-mail:461971070@qq.com。
2017年3月8日。
S781.23
责任编辑:戴芳天。
