基于ANSYS的封闭柱壳声固耦合研究
2017-09-03李智劳郭艳崔盼礼中国飞机强度研究所
李智劳,郭艳,崔盼礼中国飞机强度研究所
基于ANSYS的封闭柱壳声固耦合研究
李智劳,郭艳,崔盼礼
中国飞机强度研究所
封闭柱壳模型是生产和生活中应用比较广泛的声学模型之一,柱壳内部的声场不但会影响结构的正常工作,使结构的实用寿命减短,更有甚者,会使结构直接发生破坏,因此研究封闭柱壳的声场分布具有重要的理论意义和实用价值。本文通过ANSYS有限元软件对柱壳进行声固耦合分析,研究了谐振力激励下,柱壳内部声场分布问题以及柱壳内流体和边界吸收系数对声场分布的影响,得出了柱壳内部在不同流体和不同吸收边界条件下的声场分布及声压与声压级曲线,给出了不同流体以及不同边界条件下的声场变化规律和影响声场的因素。
封闭柱壳;声场;吸收系数
封闭柱壳是工程中重要的结构之一,比如发动机外壳,管道,储油罐等[1]。强的噪声场不但容易使结构的工作性能下降,更有甚者,还会导致结构破坏或其它不可预知的后果。另外,噪声还会产生严重的环境问题,损害人类健康。近些年来研究腔体噪声的越来越多,大多数只是对腔体做声学模态分析[2],或者仅仅对腔体在激振力作用下的声场做简单分析[3],相对来说做柱壳声场分析的还比较少。本文研究了封闭柱壳的声固耦合问题,即通过ANSYS有限元软件对柱壳进行声固耦合分析,研究了谐振力激励下,柱壳内部声场分布以及柱壳内流体和边界吸收系数对声场分布的影响。
1 声固耦合理论
为实现完整的表达流固耦合的问题,将在界面处流体声压载荷加入结构有限元方程中,得到
其中:Me为声场流体的质量矩阵,Ue为节点位移向量,Ce为流体阻尼矩阵,Ke为流体的刚度矩阵,为声压载荷向量。
其中:{N′}为离散化位移u,v,w的结构形函数矩阵,{n}为流体边界向量。

定义有限元的近似形函数为:


离散化的声波方程为
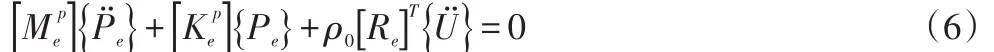

S动态有限元方程。
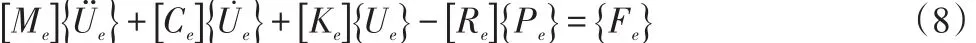
考虑界面处能量损耗的声波离散方程为
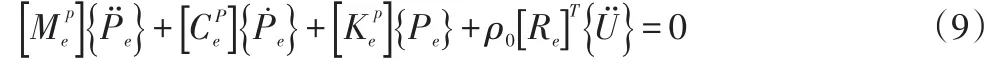
得
到完整的流固耦合问题的有限单元法离散方程:
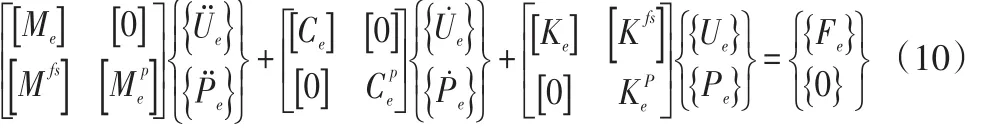
2 算例
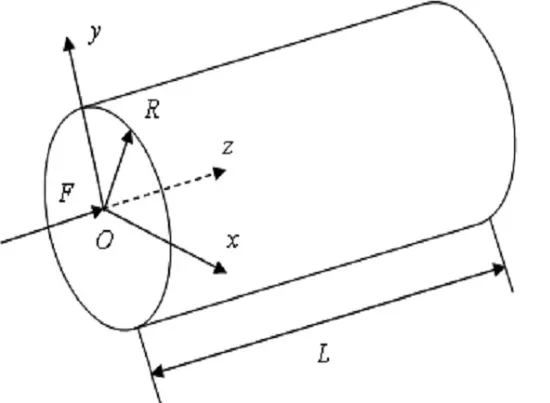
图1 几何尺寸图

图2 加载及网格图
如图1所示的封闭柱壳密度ρ=7800kg/m3,泊松比λ=0.3,半径R=1m,长度L=5m,腔内充满水,ρ水=1000kg/m3,水中声速v=1483m/s,边界为刚性边界,即边界吸收系数mu=0对声波进行全反射,没有吸收,柱壳一端约束。
图1所示为柱壳的几何尺寸图,表1为腔体中流体的密度和声速。图2为柱壳的加载及网格图。图3为柱壳在200Hz时的声压级分布,图4为518号节点的声压级曲线。

表1 流体参数

图3 200Hz时的声压级分布

图4 518号节点声压级分布
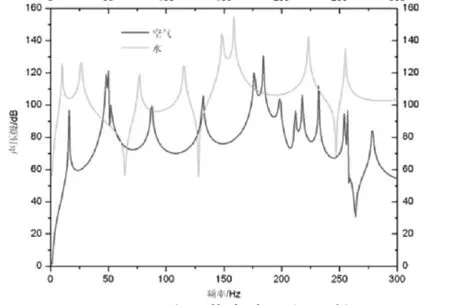
图5 518号单元节点声压级比较

图6 频率为200Hz,吸收系数为0.2时的声压级分布
从图5可以看出柱壳内流体为空气的情况下,柱壳内部的最大声压级约为132dB,并且在相同激励下,柱壳中为水时的声压级基本要要大于柱壳中为空气时的声压级。
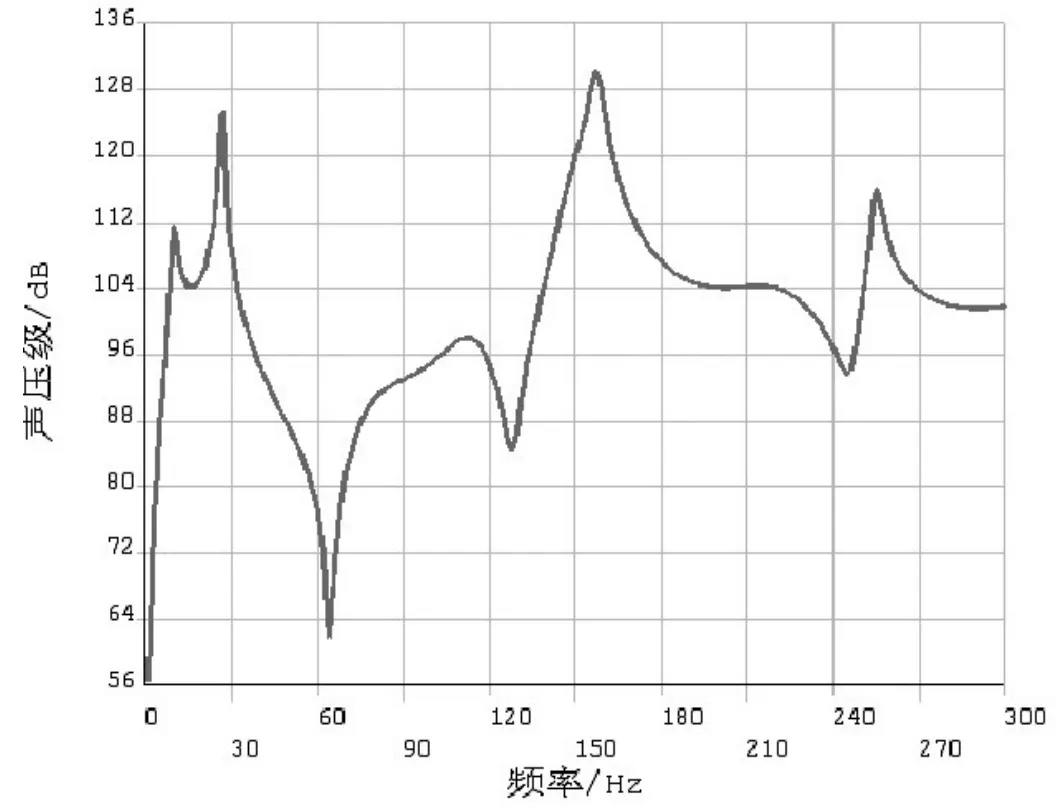
图7 518号节点声压级曲线
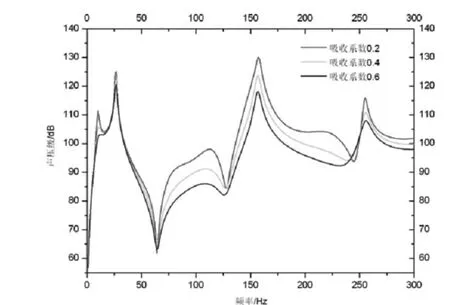
图8 518号节点在吸收系数不同时的声压级曲线
图6 为频率为200Hz,吸收系数为0.2时的声压级分布;图7为518号节点声压级曲线。从图8可以看出518号节点的声压级峰值在不同的吸收系数下,在同一频率点,很明显随着吸收系数的增大声压级逐渐减小。这是由于由全反射边界变为吸收边界时声波能量在传播的过程中在边界处会得到吸收,这在降噪和消声处理方面有重要应用价值。
3 结论
通过ansys的有限元声学分析功能,首先模拟了封闭柱壳内部充水时的声场分布,然后计算了柱壳内部流体为空气时的声场分布,最后计算了当柱壳中的流体为水时,边界吸收系数0.2,0.4,0.6时的声场分布情况。本文在计算的时候假设流体是非滞性的,实际情况中这样的流体并不存在所以最终的计算结果可能会有一定误差。另外,现实中柱壳外的空气也会对最终的计算结果又一定的影响;均匀流体也不存在;温度也会对声场有一定影响。
[1]吴九汇,陈花玲,胡选利.任意形状封闭薄壳内部声场计算的一种新方法研究[J].声学学报,2000(5):468-471.
[2]饶柱石,罗超,耿厚才,韩祖瞬.复杂封闭空间有源消声系统的建模新方法[J].振动工程学报,2003(04):415-419
[3]姚昊萍,张建润,陈南,孙庆鸿.弹性长方体封闭结构腔声辐射建模与分析[J].东南大学学报,2005(06):889-893.
[4]Jin-Meng HO.Ray acoustic and vibration of immersed thin elastic cylindrical shells excited by an on-surface source,1995(22):75-96.
[5]Li Jun,Hua Hongxing.Transient interaction of a plane acoustic wavewith an elastic orthotropic cylindricalshell,2009(47):335-345.
