一类非凸规划K-K-T点的性质及同伦方法收敛定理

孙文娟，申爱红，刘 芳

(1.沈阳理工大学 理学院，沈阳 110159；2.中国刑事警察学院 基础部，沈阳 110854 )

一类非凸规划K-K-T点的性质及同伦方法收敛定理

孙文娟1，申爱红2，刘 芳1

(1.沈阳理工大学 理学院，沈阳 110159；2.中国刑事警察学院 基础部，沈阳 110854 )

对于目标函数为凸的一类非凸规划，证明了其K-K-T点一定是局部极小点。在求解此类非凸规划时，基于可行域满足较法锥条件更弱的拟法锥、弱拟法锥等条件下，同伦方法得到的K-K-T点一定是局部极小点。对于一般非凸规划问题，证明了边界上的K-K-T点如果不是驻点，则一定是局部极小点。

非凸规划；K-K-T点；同伦方法；局部极小

应用同伦方法求解优化问题，最早见于1979年Garcia和Zangwill的工作，他们利用同伦方法求解凸规划，并证明了在一定条件下该方法是大范围收敛的。目前，同伦方法用于求解各种凸规划问题[1]的理论与算法已基本完善，而用于求解非凸规划问题的理论与算法还有待进一步研究。

自冯国忱等[2]提出了组合同伦内点法求解非凸规划问题之后，具有大范围收敛性的同伦方法，受到了诸多学者的重视，并成为非凸规划问题求解方法的研究热点之一。但利用同伦方法求解的非凸规划，可行域必须满足法锥条件，初始点也必须是内点，大大削弱了同伦方法的实用性。近二十年来，很多学者致力于研究如何减弱可行域所满足的条件及对初始点的限制条件，并取得了一定的成果[3-6]。

由于同伦方法求得的只是优化问题的K-K-T点，对于凸规划问题，K-K-T点即为最优解，但对于非凸规划问题，结论不一定成立。而就目前对非凸规划问题的研究来看，所有的实际数值算例显示，同伦算法所收敛到的K-K-T点绝大多数就是优化问题的最优解或局部极小解。此结果是否是同伦算法本身所具备的收敛性质，还是和初始点的选取有关，或是和算例中的所选优化问题的特殊性有关，目前相应理论还不完善。孙文娟等人[7-9 ]只是得到了在非凸区域满足法锥条件、同伦映射为正则映射的条件下，构造合适的同伦方程，可以收敛到局部极小解。本文在此基础上，针对目标函数为凸的一类非凸规划问题，研究其K-K-T点的性质，得到了可行域在满足较法锥条件更弱的条件下，同伦算法求解此类非凸规划的收敛定理，推广了文献[9]的结果。

1 基本概念

考虑非凸规划(NCP)问题

minf(x)

s.t.gi(x)≤0,i=1,2,…,m

(1)

式中：x∈Rn；f(x)、gi(x)(i=1,2,…,m)为二阶连续可微函数(不必凸)。

设Ω={x∈Rn:gi(x)≤0,i∈{1,2,…,m}}为(NCP)的可行域，Ω0={x∈Rn:gi(x)<0,i∈{1,2,…,m}}为(NCP)的严格可行域，∂Ω=ΩΩ0为Ω的边界集，I(x)={i∈{1,2,…,m}:gi(x)=0}为在x点的紧指标集。

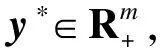
Yg(x)=0,

y≥0,g(x)≤0

(2)

式中Y=diag(y)。系统(2)称为问题(1)的K-K-T系统或一阶必要条件。如果点(x*,y*)满足式(2)，那么称x*为问题(1)的K-K-T点，y*为Lagrange乘子。如果f,gi是凸函数，那么K-K-T点就是问题(1)的最优解。

定义2设Ω为非空子集，x*∈Ω。非零向量d∈Rn称为在x*处的可行方向，若存在δ>0使得

x*+αd∈Ω,其中α∈(0,δ)。

2 求解不同非凸区域的同伦方法

冯国忱等[2]提出了可行域Ω满足法锥条件，即x∈∂Ω有

H(t,ω)=

(3)

刘庆怀等[5-6]研究了在较法锥条件更弱的拟法锥条件及弱拟法锥条件下，通过定义正独立映射，构造修正的组合同伦方程，进一步拓宽了同伦方法求解非凸规划的范围。

所谓Ω满足拟法锥条件是指：若存在关于g(x)正独立光滑映射ηi(x)(i=1,2,…,m)，且满足∀x∈∂Ω,有Ø。Ω满足弱拟法锥条件是指：存在⊂Ω0,∀x∈∂Ω,满足Ø。

显然若Ω满足法锥条件或拟法锥条件，则一定满足弱拟法锥条件，但反之不然。

假设条件：

(1)Ω为连通、有界闭集，Ω0非空；

(2) 任意x∈∂Ω,ηi(x)(i=1,2,…,m)关于g(x)关于是正独立的。

(3)Ω关于ηi(x)(i=1,2,…,m)满足弱拟法锥条件。

构造同伦方程

(4)

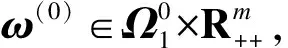
3 一类非凸规划的K-K-T点性质及同伦方法收敛定理

考虑非凸规划问题

minf(x)

s.t.gi(x)≤0,i=1,2,…,m

(5)

式中：x∈Rn；f(x)为二阶连续可微凸函数；gi(x)(i=1,2,…,m)为二阶连续可微函数(不必凸)。

引理1[9]设x*是K-K-T点，则对在x*点的每一个可行方向d,有

dTgi(x*)≤0,i∈I(x*)

定理2若x*是K-K-T点，则x*一定是问题(5)的局部极小点。

证明1) 若x*∈Ω0，由于f(x)为凸函数，显然x*为局部极小点。

2) 若x*∈∂Ω，则I(x*)≠Ø。

故在点x*处无可行下降方向，x*一定是局部极小点。

综上所述，若x*是K-K-T点，x*是问题(5)的局部极小点。

由定理2及其证明，易得如下定理。

定理3对于一般非凸规划问题(1)，K-K-T点x*若在区域边界上，且不为驻点(即f(x*)≠0)，则x*一定是局部极小点。

定理4对于问题(5)，在可行域满足更弱(拟法锥、弱拟法锥等)条件下，构造修正同伦方程，同伦方法得到的K-K-T点都是局部极小点。

4 结论

研究了对于目标函数为凸的一类非凸规划问题K-K-T点的性质，并得到了同伦方法的收敛性定理。证明了这类非凸规划问题，K-K-T点一定是问题的局部极小点，因此在用同伦方法求解此类非凸规划时，当可行域在更弱(拟法锥、弱拟法锥等)条件下，只要同伦路径存在并且收敛到K-K-T点，那么该收敛点一定是局部极小点，从而推广了文献[9]的结果。而对于目标函数非凸的非凸规划问题，一些数值算例显示，在比正则映射更弱的条件下，可行域满足较法锥条件更弱条件时，也能收敛到局部极小点，但没有相应的理论依据，这将是今后的研究方向。

[1]王宇.计算机优化同伦内点法[M].大连：大连理工大学出版社，1991.

[2]FENG Guochen,LIN Zhenghua,YU Bo.Existence of interior pathway to a Karush-Kuhn-Tucker point of a nonconvex programming problem [J].Nonlinear Analysis,Theory,Methods and Applications,1998,32(6)：761-768.

[3]YU Bo,FENG Guochen,ZHANG Shaoliang.The aggregate constraint homotopy method for nonconvex nonlinear programming[J].Nonlinear Analysis,Theory,Methods &Applications,2001(45):839-847.

[4]商玉凤.马蹄形非凸区域上的伪锥构造及其在同伦内点法中的应用[D].长春：吉林大学，2001.

[5]刘庆怀，于波，冯国忱.基于拟法锥条件的非凸非线性规划问题的同伦内点法[J].应用数学学报，2003，26(2)：371-377.

[6]刘庆怀，张春阳，张树功.弱拟法锥条件下非凸优化问题的同伦算法[J].应用数学学报，2011，34(6)：996-1006.

[7]孙文娟，李忠范，王彩玲,等.同伦方法求解无约束非凸优化问题的局部极小[J].东北师大学报：自然科学版,2009,41(3):17-20.

[8]孙文娟，王彩玲.同伦方法求解无界域上非凸规划问题的收敛性定理[J].应用数学，2012,25(4):732-737.

[9]孙文娟，赵巍巍.同伦方法求解一类非凸规划问题的新的收敛性定理[J].沈阳理工大学学报，2014，33(3)：32-34.

(责任编辑：马金发)

PropertyoftheK-K-TPointandConvergenceTheoremofHomotopyMethodforaClassofNonconvexProgramming

SUN Wenjuan1，SHEN Aihong2，LIU Fang1

(1.Shenyang Ligong University,Shenyang 110159,China；2.Foundation department,National Police University of China,Shenyang 110854,China)

It is proved that,the K-K-T point of a class of nonconvex programming problem,objective function of which is convex,is a local minimum.For this nonconvex programming problem under the quasi-normal cone condition or the weak quasi-normal cone condition,which are weaker than normal,cone condition the K-K-T point got by homotopy method must be a local minimum.It is also proved that,for general nonconvex programming problem,if the K-K-T point on the boundary is not a stationary point,it must be a local minimum.Keywordsnonconvex programming;K-K-T point;homotopy method;local minimum

2016-09-20

辽宁省教育厅科学技术研究项目(LG201615)

孙文娟(1982—)，女，讲师，研究方向：最优化理论与算法;通讯作者：刘芳(1979—)，女，讲师，研究方向：应用数学。

1003-1251(2017)04-0102-03

O221

A