基于刀具实际廓形的刀位轨迹计算方法

赵 萍

(辽宁省交通高等专科学校 机电工程系，沈阳 110122)

基于刀具实际廓形的刀位轨迹计算方法

赵 萍

(辽宁省交通高等专科学校 机电工程系，沈阳 110122)

为解决由于刀具磨损和制造误差对复杂曲面精加工的影响，根据刀具的实际廓形计算刀位轨迹，首先利用机器视觉测量系统检测刀具的廓形，从而获得实际刀具曲面，然后采用自适应等参数法规划加工路径，最后利用最小有向距离原理和曲面空间离散的方法计算刀具曲面和工件曲面的最小有向距离，通过调整刀具位姿，使刀具的刀触点恰好在工件的理论面上，从而得到优化的刀位轨迹。实验表明，采用这种轨迹计算方法编制的数控加工程序能够加工出满足精度要求的曲面。

复杂曲面加工；刀位轨迹计算；机器视觉测量；最小有向距离算法

随着机械工业的不断发展，各种拥有复杂曲面的机械零件得到了越来越广泛的应用，如汽车车身、飞机机身、汽轮机叶片、模具等。刀位轨迹计算一直是曲面数控加工中的热点问题，从70年代至今，人们已经从不同的角度、不同的应用背景提出了很多方法，现在比较成熟的有等距面法[1]、多面体法[2-3]、等参数线法[4]、投影法[5]等。这些算法在解决刀位轨迹计算问题中各有特点，但它们都有一个共同的特点：在刀位轨迹计算中，根据刀触点和理想的刀具模型计算刀位点。而实际上，刀具在加工的过程中都会产生磨损，并且自身也存在制作误差，故刀具的廓形不是理想廓形，在精加工中对曲面的加工精度有很大影响。

为解决以上问题，本文在检测刀具实际包络廓形的基础上，提出了一种优化算法，首先应用机器视觉测量技术快速及时地测量刀具的实际包络廓形，然后规划曲面的加工路径，最后应用最小有向距离原理[6]和空间离散的思想计算实际刀具曲面和工件曲面的最小有向距离，由此来确定最终的刀位点，该方法既消除了刀具制造误差和磨损对曲面精加工的影响，又消除了局部干涉的影响，可以得到无干涉的刀位轨迹。

1 刀具廓形的测量

1.1 测量系统的搭建

本文搭建了如图1所示的机器视觉测量系统，通过提高系统的硬件分辨力和图像处理软件的边缘检测精度来提高系统的测量精度。

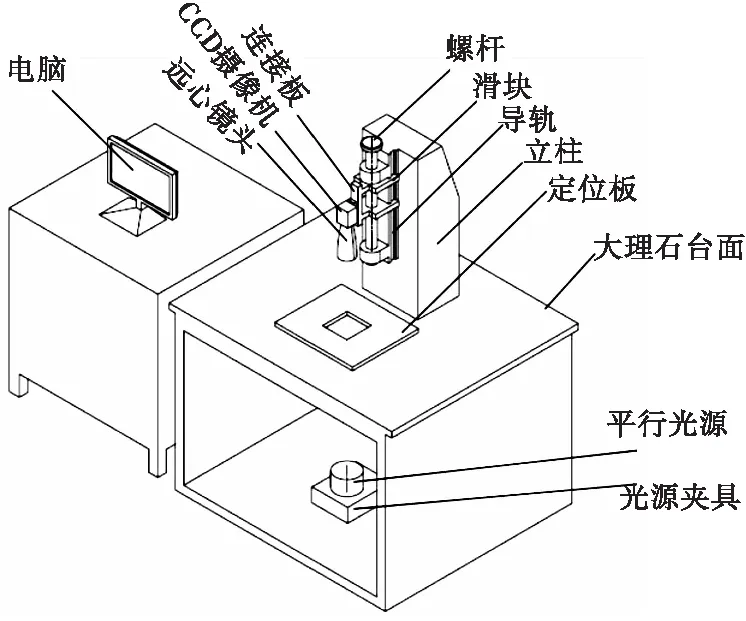
图1 机器视觉测量系统

在硬件配置上：像机采用德国Basler公司的piA2400-17gc CCD摄像机，分辨率为500万(2448×2050)像素，靶面尺寸 2 /3"(W=8.8mm，H=6.6mm)，芯 片 为 Sony ICX625)；镜头采用日本 Computar 公司的M5018-MP2镜头，焦距50mm，光圈F1.4～F16，水平视角10.5°。照明系统的设计是视觉系统设计中的关键环节，决定成像的质量，好的光照系统会极大地增大被测物与背景之间的对比度，降低系统对图像处理算法的要求，提高边缘的定位精度。为消除光反射带来的测量不确定性，本文利用透镜折射原理设计了特定光源，将激光点光源转化为宽束平行光，其结构如图2所示。

图2 平行光源结构图

图像处理系统软件的核心是边缘检测算法，该算法的精度决定了图像测量系统的精度。但在成像过程中由于光照和物体本身的反射、透射特性具有一定的连续性，使得原本呈阶梯状的边缘部分呈现光滑过渡，因此很难精确地找到测量对象的边缘[7]。如果要使图像测量系统的精度达到微米级，就需要另辟新径，从根本上解决边缘检测的难点问题。为达到精确定位的目的，本文按照以下步骤来检测边缘[8]：图像滤波(在消除随机噪声的同时保持梯度不变)——边缘粗定位(根据边缘特征提取出整像素精度边缘)——边缘精定位(对检测到的边缘点在其像素区域内进一步定位)——边缘曲线拟合(为进一步降低随机噪声和计算误差，对边缘进行分段拟合)，具体流程见图3所示。

1.2 刀具包络廓形的测量

本文采用“复印”法测量刀具的包络廓形，将一个40mm×40mm×5mm样板安装在机床上，让实验刀具在给定的切削速度和进给量下切削样板，直至其全部切削刃的包络廓形都“复印”在样板上。然后使用如图1所示的机器视觉测量系统测量“复印”在样板上的廓形。检测流程如图3所示，使用摄像机拍摄的图像如图4a所示，滤波的效果如图4b所示，提取的单像素边缘如图4c所示，基于facet模型计算的亚像素边缘如图4d所示，利用综合标定函数校正的边缘如图4e所示，利用最小二乘法分段拟合的边缘如图4f所示。

图3 基于机器视觉的高精度边缘检测流程

图4 提取刀具实际包络廓形

将检测的刀具实际包络廓形旋转即能获得刀具曲面。

2 加工路径的规划

加工路径规划是数控加工技术的核心内容。在关于加工路径规划理论方面，国内外学者做了大量的研究，提出了不少算法，这些算法的提出旨在提高加工效率，改善加工精度以及零件的表面质量。现在比较成熟的有等参数法、截平面法和等残留高度法。其中，等参数线轨迹以其简单可靠的特点一直在多轴数控加工中占据着重要地位，该方法的基本思想是保持u、v参数中任一参数不变，将参数平面上的等参数线(u线或v线)映射回参数曲面，生成刀具运动轨迹；该方法直观、简单，在实际生产中得到广泛应用；但由于加工行距只依赖于最大残留高度，从而使得局部区域加工轨迹过于密集，影响表面加工质量。为此本文采用自适应等参数法[9-10]，根据给定的精度要求和工件变化曲率规划加工路径，使在曲率变化较小的曲面轨迹稀疏一些，曲率变化较大的曲面轨迹密集一些，从而保证曲面加工的质量和效率。

以刀具沿v向走刀为例，具体计算时，首先选u=0取作为初始参数曲线，然后利用圆弧插补法确定走刀步长，计算公示为

(1)

式中：λ为走刀步长；ε为离散精度；ρ为上一刀触点处的法曲率半径。

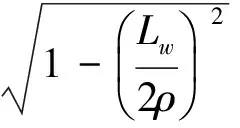
(2)

式中：ρ为逼近圆弧的半径；h为加工曲面的残留高度；R为刀具有效切削半径；Lw为加工行距。

当残留高度远小于曲率半径，即满足条件h≪p时，公式(2)可以简化为

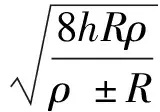
(3)

当刀触点局部区域为凸曲面时，取正号；反之取负号。

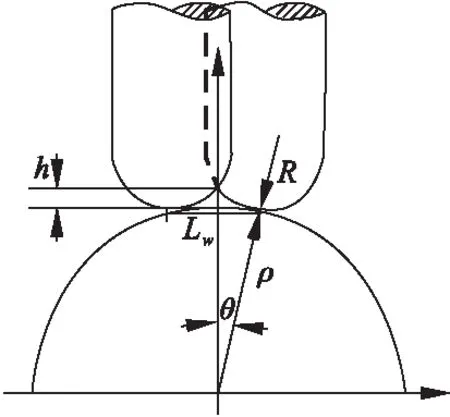
图5 刀具-曲面的几何关系

求取最小加工行距，即

(4)

(5)

将p1在p0处进行泰勒展开，并略去二阶以上的各项，可得

(6)

(7)

将参数增量Δu代入曲面方程即可得到对应的刀触点，连接所有刀触点即可得到下一条刀位轨迹。式中的正负号根据加工方向确定。

重复上述过程，直到u≥1为止。

3 刀位轨迹的优化

根据包络原理，在曲面加工中，工件曲面是由刀具曲面包络而成，因此在刀触点计算时，只要能保证刀具表面恰好是工件表面上的一个包络位置，刀触点就位于工件理论曲面上。但在实际加工中，由于刀具的磨损和制造误差，可能会在刀触点位置出现欠切或过切，为此本文利用最小有向距离原理和空间曲面离散的思想，将刀具曲面和工件曲面进行离散，通过计算每个刀触点处刀具实际曲面与工件曲面的最小距离，对刀具的位姿进行调整，使加工轨迹恰好位于工件曲面，从而提高曲面的加工质量。

(8)

刀具曲面和工件曲面在z方向的最小距离为

L=min{d1,d2,…,dk}

(9)

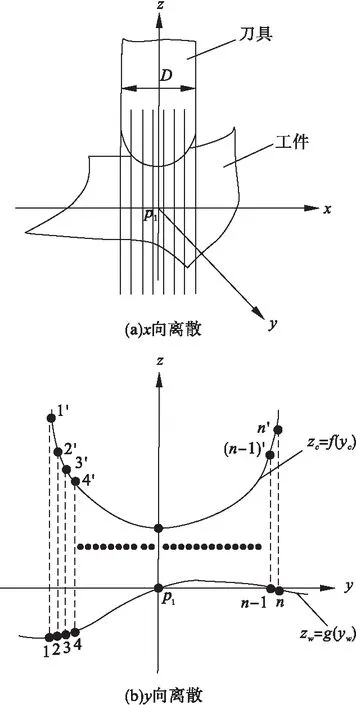
图6 曲面空间离散示意图

图7 刀位优化示意图

4 实验

本算法已经实现并对多个实例进行了验证，图8显示了叶片精加工的刀位轨迹。可以注意到本算法生成的轨迹都在叶片的理论曲面上，由于轨迹就是实际的刀触点的连线，因此在加工中不会出现欠切或过切，由此所加工的叶片精度得到很大提高。图9是依据本文算法采用立式加工中心VMC1300P加工的叶片(材料为45#钢)，精加工切削参数为：主轴转速4000r/min、进给速度1000m/min。

图8 叶片的精加工刀位轨迹

图9 加工的叶片

利用三坐标测量仪按照等高线测量路径检测叶片不同区域，检测结果表明，采用该方法加工的叶片满足精度要求。

5 结论

(1)本文基于最小有向距离原理分析刀具曲面、刀具包络面和加工曲面之间的关系，确定单个刀位处刀具曲面和工件曲面之间的相对几何位置关系，建立基于实际刀具廓的刀位计算方法，消除由于刀具磨损和制作误差引起的曲面加工误差，通过实验证明，采用该方法能够加工出满足精度要求的曲面。

(2)利用机器视觉测量技术可以快捷有效地提取旋转刀具的廓形，实验证明，本文搭建的机器测量系统可达到微米级，可用于精密样板、平板类高精度零件的检测。

(3)应用空间曲面离散化思想计算最小有向距离，具有对曲面适应范围广、计算量小、计算速度快等特点，适用于复杂曲面的加工。

[1]G.W.Vickers,H.Li,Z.Dong.Automated rough machining of curved surfaces[J].Proceedings of the CSME Forum,1993(17):647-657.

[2]Z.Dong,H.Li,G.W.Vickers.Optimal rough machining of Sculptured parts on a CNC milling machine[J].Journal of Engineering for Industry,1993(115):424-431.

[3]J.P.Duncan,S.G.Mair.Sculptured surfaces in engineering and medicine[M],USA:Cambridge University Press,1983.

[4]W.He,M.Lei,H.Bin.Iso-parametric CNC tool path optimization based on adaptive gridgeneration[J].The International Journal of Advanced Manufacturing Technology,2009,41(5):538-548.

[5]孟书云.高精度开放式数控系统复杂曲线曲面插补关键技术研究[D].南京:南京航空航天大学,2006.

[6] 赵文珍，张新建.基于最小有向距离原理的无干涉刀位轨迹计算[J].机械工程师，2007，27(10):7-9.

[7]赵萍，蔡清华，赵文珍.一种适用于高精度视觉测量的边缘检测算法[J].制造业自动化，2015，37(3):1-4.

[8]于起峰，尚洋.摄像测量学原理与应用研究[M].北京：科学出版社，2009.

[9]张鸣.复杂型腔数铣削加工路径规划策略及应用研究[D].沈阳：中科院沈阳自动化研究所，2011.

[10]徐金亭.精密复杂曲面重构与多轴数控加工刀位规划策略[D].沈阳：中科院沈阳自动化研究所，2009.

(责任编辑：赵丽琴)

ToolPathCalculationMethodBasedontheActualToolProfile

ZHAO Ping

(Liaoning Province college of communication,Shenyang 110122,China)

Due to tool wear and errors in the manufacturing process,calculating the tool path based on the tool theory model has a great deal of influence on the accuracy of surface finishing machining.In order to solve the above problem,the paper calculates the cutter tool path according to the actual profile of the cutter.Firstly,the tool profile is measured by the machine vision measurement system to obtain the actual tool surface,then the adaptive parameters algorithm is used to plan the machining path,finally the minimal orientation-distance of the cutter surface and the workpiece surface is obtained based on the minimal orientation-distance algorithm and curved space discrete algorithm.By adjusting the tool position,the cutter contact is set just on the workpiece theory,so as to optimize the tool path.The results show that it can produce the surface meeting precision requirement with the NC programming by this method.Keywordscomplex curved surface machining;tooling path calculation;machine vision measurement technology;minimal orientation-distance algorithm

2017-03-02

辽宁省博士启动基金计划项目(20141172)；辽宁省教育厅科研项目(L2014513)

赵萍(1979—),女,副教授,博士,研究方向：复杂曲面加工、精密测量。

1003-1251(2017)04-0073-05

TH164

A