薄圆盘直径端点之间电阻的研究
2017-09-01惠小强
王 岚 惠小强
(1西安邮电大学理学院; 2西安邮电大学物联网与两化融合研究院,陕西 西安 710061)
薄圆盘直径端点之间电阻的研究
王 岚1惠小强2
(1西安邮电大学理学院;2西安邮电大学物联网与两化融合研究院,陕西 西安 710061)
针对薄圆盘直径端点之间电阻难以利用传统直接积分法或数值解法测量的问题,本文利用有限元分析法研究了薄圆盘直径端点之间电阻的测量方法。利用Comsol multiphysics设计薄圆盘电阻测量平台,通过在薄圆盘直径端点设计电极,研究了薄圆盘直径端点之间电阻随薄圆盘半径、电极位置、薄圆盘上小孔位置和大小的变化规律;利用最小二乘法拟合薄圆盘直径端点之间电阻表达式,实现薄圆盘直径端点之间电阻间接测量;在典型条件下,利用直接积分测量法对上述测量方法进行验证,结果表明本文提出的方法误差较小。本文研究工作对薄圆盘电阻的设计具有指导意义,且该研究方法还可以推广用于其他形状电阻的设计。
薄圆盘;电阻;Comsol multiphysics
稳恒条件下导体内电势/电流的分布、不规则或不均匀导体电阻的测量等都是电磁学应用研究中的基本问题[1,2]。目前,针对高对称性物体主要通过直接积分测量法计算电阻值,而针对低对称性物体一般采用数值解法[3,4]。
纵观国内外公开文献[5-8],尚未见到有关薄圆盘直径端点之间电阻研究的相关报道或文献,其主要原因是薄圆盘中电流方向和等势线的关系复杂,其电阻难以直接利用直接积分测量法或数值解法计算。
针对上述问题,本文研究了薄圆盘直径端点之间电阻的测量方法。首先,利用Comsol multiphysics[9]软件设计了薄圆盘电阻测量平台,研究了薄圆盘直径端点之间电阻随薄圆盘半径、电极位置、薄圆盘上小孔位置和大小等因素的变化规律;其次,利用最小二乘法拟合薄圆盘直径端点之间电阻表达式,实现薄圆盘直径端点之间电阻间接测量;最后,在典型条件下,利用直接积分测量法对上述测量方法进行验证。
1 薄圆盘直径端点之间电阻测量平台设计
为实现薄圆盘直径端点之间电阻测量平台设计,本文利用有限元分析法建立电导率固定、半径为a的薄圆盘;在薄圆盘上挖一个半径为r的小孔,并补上不同电导率的介质;在薄圆盘边缘设计电极,如图1所示。

图1 薄圆盘直径端点之间电阻测量平台示意图
在Comsol multiphysics软件AC/DC模块中通过设置薄圆盘属性(半径、厚度、电导率)、电极位置和半径、小孔属性(半径、位置及电导率)、指定电流输入端和输出端建立实验模型。在Comsol multiphysics软件后处理模式下研究薄圆盘中电势、电流分布的模拟效果,并在此基础上分析不同实验条件下薄圆盘的电势、电流变化,实现薄圆盘电阻变化规律研究。
2 薄圆盘直径端点之间电阻测量方法研究
针对特定材质和厚度的薄圆盘,影响薄圆盘直径端点之间电阻的主要因素有: (1)薄圆盘半径;(2)小孔半径和位置;(3)电极位置。因此,为实现薄圆盘直径端点之间电阻测量,本文分别研究了薄圆盘直径端点之间电阻随薄圆盘半径、电极位置、薄圆盘上小孔位置和大小的变化规律,并在此基础上利用最小二乘法拟合薄圆盘直径端点之间电阻表达式。
2.1 薄圆盘半径对薄圆盘直径端点之间电阻的影响分析
为研究薄圆盘半径对薄圆盘直径端点之间电阻的影响,本文设置薄圆盘厚度(0.1cm)和电导率(15S/m)、端点电极的位置(如图1所示)和半径(0.25cm)、电极输入电流(1A)不变,圆盘半径a变化范围为0≤a≤10cm。根据电极输入电流及薄圆盘直径端点之间电势模拟结果,计算得到薄圆盘直径端点之间电阻变化规律如图2所示。
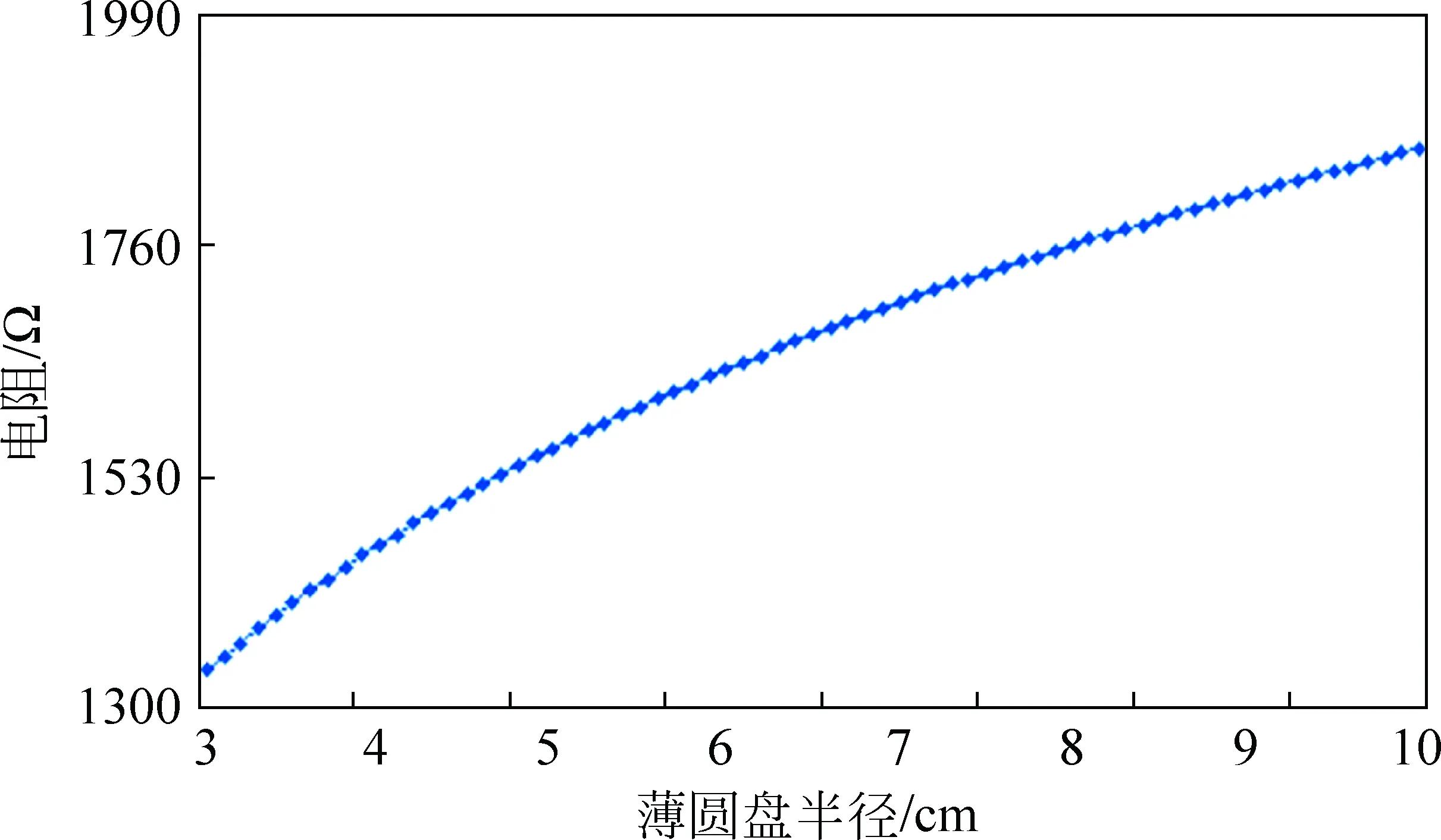
图2 薄圆盘直径端点之间电阻随薄圆盘半径的变化规律
从计算结果可以看出:薄圆盘直径端点之间电阻随薄圆盘半径的增大而增大。根据计算结果,利用最小二乘法可以得到薄圆盘直径端点之间电阻R与薄圆盘半径a之间关系为
R=-1.66×10-3a6+7.63×10-2a5-1.49a4+16.03a3-106.10a2+480.70a+520.10
(1)
拟合结果拟合度为1.0(拟合度越接近1.0表示拟合结果越准确)。
2.2 薄圆盘上小孔半径及位置对薄圆盘直径端点之间电阻的影响分析
1) 小孔半径对薄圆盘直径端点之间电阻的影响分析
为研究小孔半径对薄圆盘直径端点之间电阻的影响,本文设置薄圆盘尺寸(厚度为0.1cm、半径为10cm)和电导率(15S/m)、端点电极的位置(如图1所示)和半径(0.25cm)、电极输入电流(1A)、小孔位置(位于薄圆盘中心)不变,小孔半径变化范围为0≤r≤9cm。根据电极输入电流及薄圆盘直径端点之间电势模拟结果,计算得到薄圆盘直径端点之间电阻变化规律如图3所示。
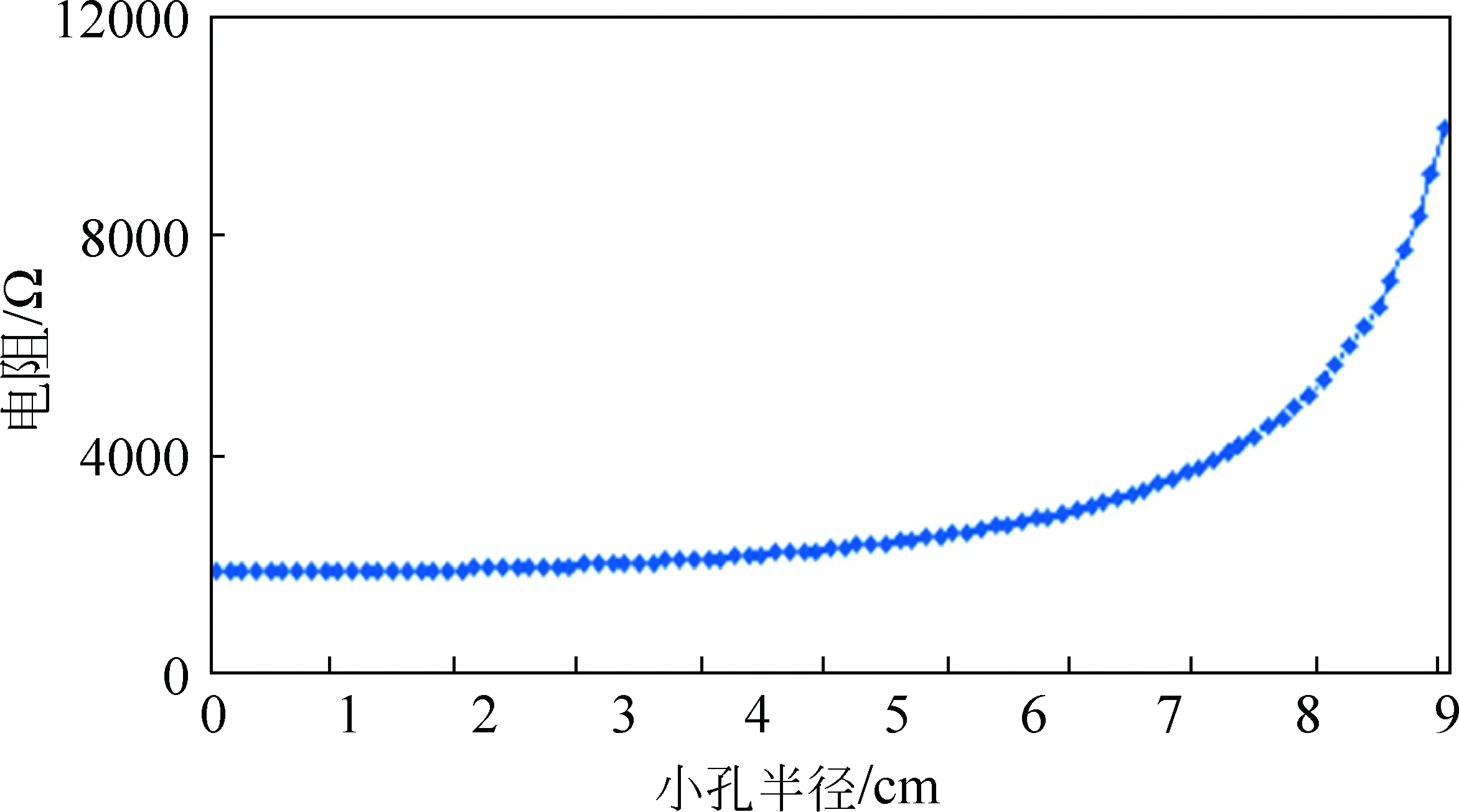
图3 薄圆盘直径端点之间电阻随小孔半径的变化规律
从计算结果可以看出:薄圆盘直径端点之间电阻随小孔半径增大呈递增的趋势;小孔半径越大,薄圆盘直径端点之间电阻增大的速度越快。根据计算结果,利用最小二乘法可以得到薄圆盘直径端点之间电阻R与小孔半径r之间关系为
R=0.43r6-9.84r5+85.52r4-346.10r3+
666.20r2-472.20r+1929
(2)
拟合结果拟合度为0.9993。
2) 小孔位置对薄圆盘直径端点之间电阻的影响分析
为研究小孔位置对薄圆盘直径端点之间电阻的影响,本文设置薄圆盘尺寸(厚度为0.1cm、半径为10cm)和电导率(15S/m)、端点电极的位置(如图1所示)和半径(0.25cm)、电极输入电流(1A)不变,分别针对小孔位于薄圆盘x轴或y轴上、小孔位于薄圆盘上任意位置两种情况,研究小孔位置变化对薄圆盘直径端点之间电阻的影响。
(1) 小孔位于薄圆盘x轴或y轴上
设置小孔圆心分别位于x轴、y轴上,小孔半径r满足0.5≤r≤2.5cm。根据电极输入电流及薄圆盘直径端点之间电势模拟结果,计算得到薄圆盘直径端点之间电阻变化规律如图4所示。
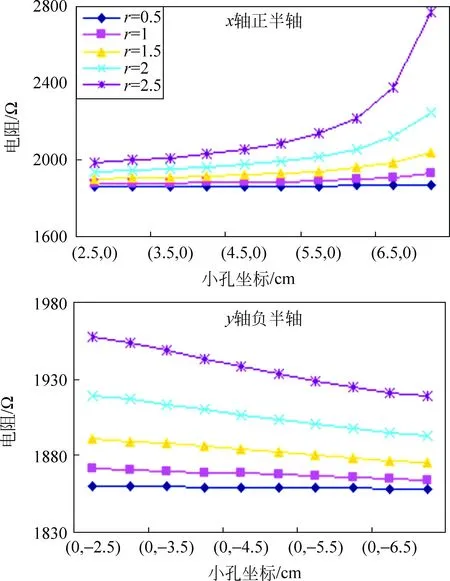
图4 薄圆盘直径端点电阻随小孔位置的变化规律

图5 薄圆盘等分示意图
从计算结果可以看出: ①当小孔位于x轴上时,小孔越靠近薄圆盘边缘位置,薄圆盘直径端点之间电阻越大;针对同一小孔位置,薄圆盘直径端点之间电阻随小孔半径的增大而增大;小孔越靠近薄圆盘边缘位置,电阻随小孔半径递增的趋势越明显;②当小孔位于y轴上时,小孔越靠近薄圆盘边缘位置,薄圆盘直径端点之间电阻越大小;针对同一小孔位置,薄圆盘直径端点之间电阻随小孔半径的增大而增大;小孔越靠近薄圆盘中心位置,电阻随小孔半径递增的趋势越明显。
(2) 小孔位于薄圆盘上任意位置
为研究任意位置小孔对薄圆盘直径端点之间电阻的影响,本文将薄圆盘分为4个象限,每个象限等分为8份,如图5所示。设置小孔圆心与x轴的夹角θ(如图1所示)变化范围为π/32≤θ≤61π/32、小孔圆心到大圆圆心的距离ρ变化范围为3.4cm≤ρ≤5.8cm。根据电极输入电流及薄圆盘直径端点之间电势模拟结果,计算得到薄圆盘直径端点之间电阻变化规律如图6所示。
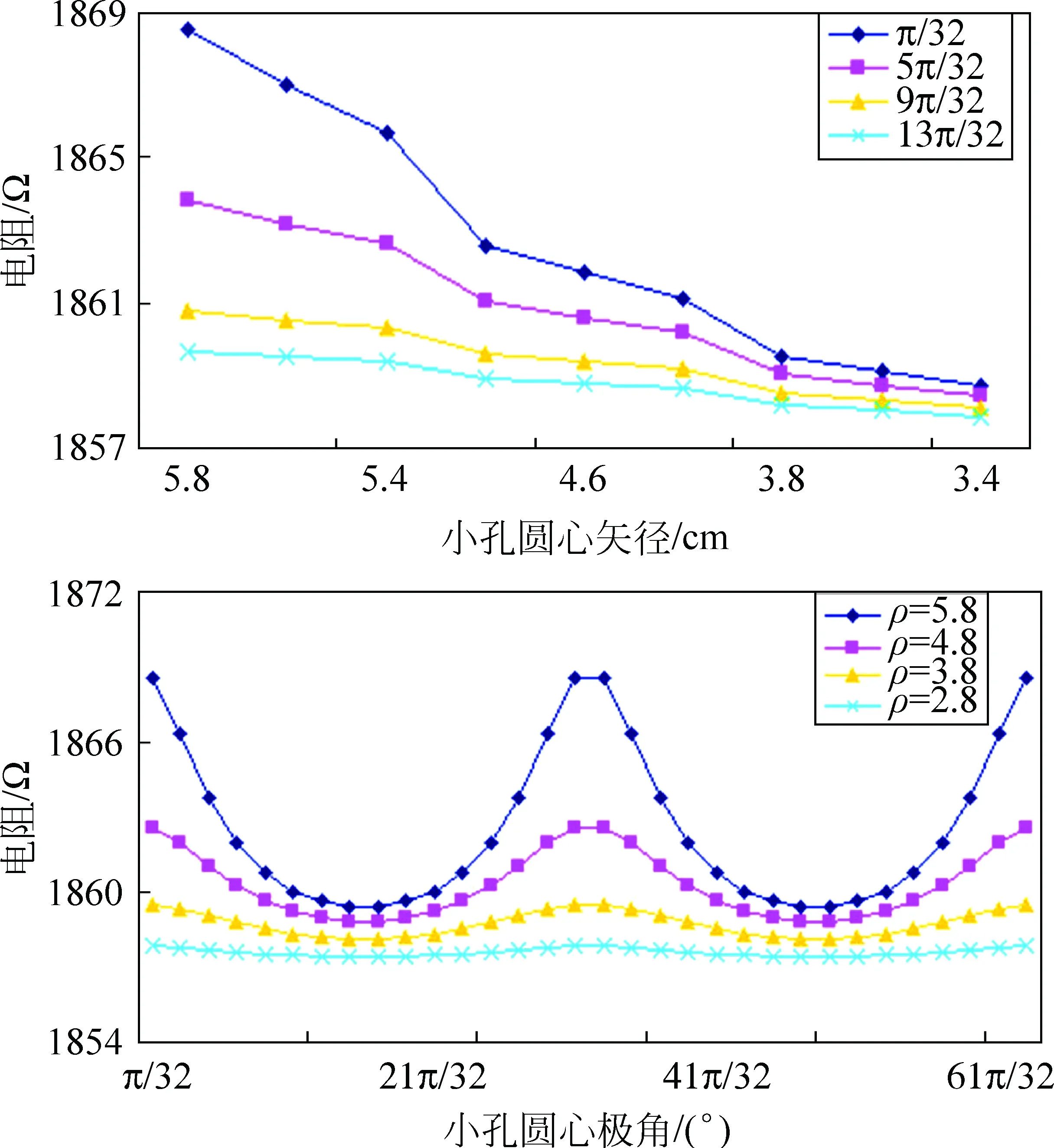
图6 薄圆盘直径端点电阻随小孔位置的变化规律
从计算结果可以看出: ①小孔圆心与x坐标轴的夹角越大,薄圆盘直径端点之间电阻在Ⅰ/Ⅲ象限呈递减的趋势,而在Ⅱ、Ⅳ象限呈递增趋势。即小孔越靠近y轴,薄圆盘直径端点之间电阻越小;②当小孔圆心与x坐标轴的夹角相同时,小孔距离薄圆盘圆心的距离越小,薄圆盘直径端点之间电阻越小。
2.3 电极半径对薄圆盘直径端点之间电阻的影响分析
为研究电极半径对薄圆盘直径端点之间电阻的影响,本文设置薄圆盘尺寸(厚度为0.1cm、半径为10cm)和电导率(15S/m)、端点电极的位置(如图1所示)、电极输入电流(1A)、小孔位置(位于薄圆盘中心)和半径(1.5cm)不变,电极半径变化范围为0.1≤re≤0.25cm。根据电极输入电流及薄圆盘直径端点之间电势模拟结果,计算得到薄圆盘直径端点之间电阻变化规律如图7所示。
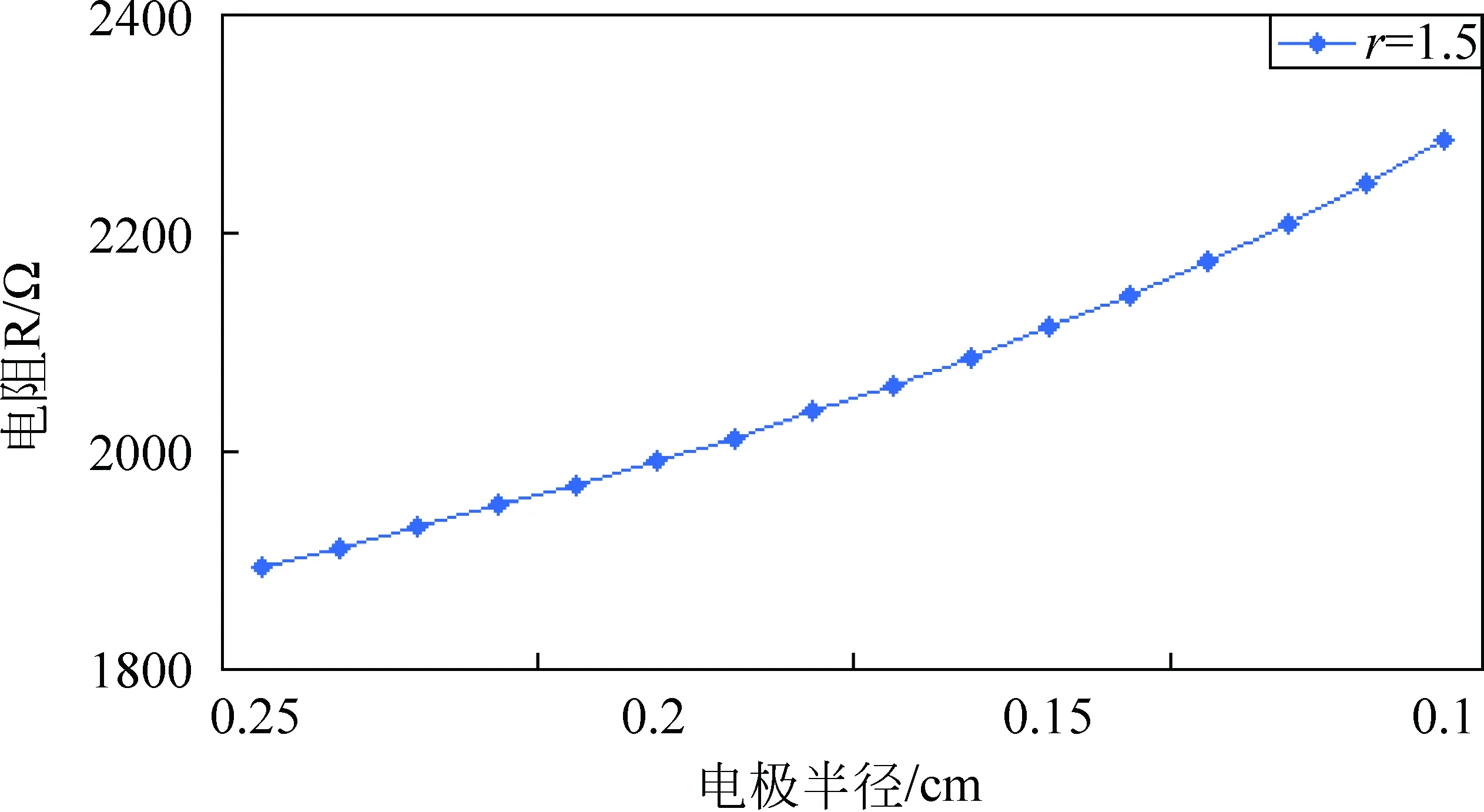
图7 薄圆盘直径端点电阻随电极半径的变化规律
从计算结果可以看出:薄圆盘直径端点之间电阻随电极半径的减小而增大。根据计算结果,利用最小二乘法可以得到薄圆盘直径端点之间电阻R与小孔半径re之间关系为
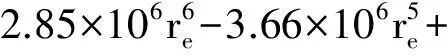

(3)
拟合结果拟合度为1.0。
3 验证与分析
为验证上文所述薄圆盘直径端点之间电阻的测量方法,本文在特定条件下对上述测量方法进行验证:设置薄圆盘厚度为0.1cm、半径为10cm、电导率为15S/m,电极输入电流(1A),小孔位于圆心、半径为4.5cm,端点电极半径为0.25cm,电极内切于薄圆盘、外切于小孔(如图8(a)所示)。此时薄圆盘直径端点之间的电阻R相当于两个并联的薄长方体的电阻(如图8(b)所示),利用上述方法可计算得到直径端点之间的阻值R为19898.61847Ω。
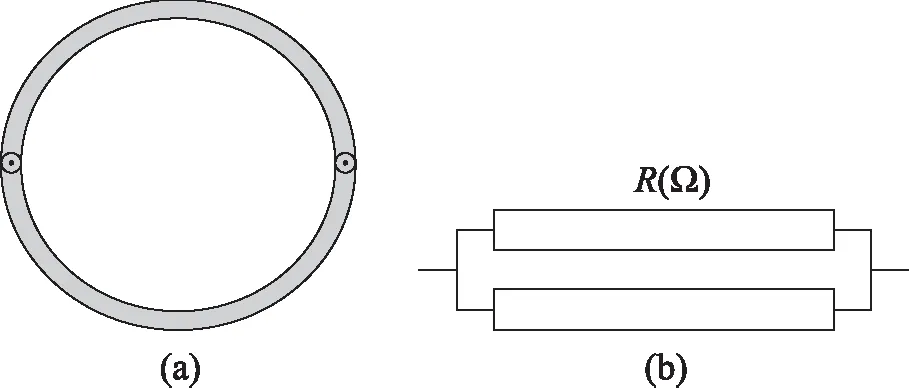
图8 特定条件下电极位置示意图(a) 电极位置示意图; (b) 薄圆盘等效并联电阻示意图
(4)
则上文所述薄圆盘直径端点之间电阻测量方法相对误差为
(5)
由计算结果可以看出,本文提出的薄圆盘直径端点之间电阻测量方法的误差较小。
4 结语
本文借助Comsolmultiphysics软件,利用有限元分析法实现了薄圆盘直径端点之间电阻的测量,并在此基础上研究了不同因素对薄圆盘直径端点之间电阻的影响。研究结果表明:①本文提出的薄圆盘直径端点之间电阻测量方法的误差较小;②当电极参数固定时,薄圆盘直径端点之间电阻随薄圆盘半径的增大而增大;③当薄圆盘参数固定时,薄圆盘直径端点之间电阻随电极半径增大而减小,随电极与薄圆盘圆心之间距离的增大而减小;④薄圆盘上小孔越靠近y轴,薄圆盘直径端点之间电阻越小。本文研究工作对薄圆盘电阻的设计具有指导意义,且该研究方法还可以推广用于其他形状电阻的设计。
[1] 李静.有限元方法在电磁场分析中的研究[D]. 重庆: 重庆师范大学, 2011. Li Jing. The Finite element method be used in electromagnetic field analysis[D]. Chongqing: Chongqing Normal University, 2011. (in Chinese)
[2] 李为峰. 接地网电阻检测方法的研究[D]. 西安: 西安理工大学, 2009. Li Weifeng. The Research on resistance measuring method for grounding grids[D]. Xi’an: Xi’an University of Technology, 2009. (in Chinese)
[3] Miroslav Ŝimandl,Jaroslav Ŝvácha. Separation approach for numerical solution of the fokker-planck equation in estimation problem[J]. IFAC Proceedings Volumes, 2005, 38(1).
[4] 倪兴. 常微分方程数值解法及其应用[D]. 北京: 中国科学技术大学, 2010. Ni Xing. Numerical solution of ordinary differential equations and its application[D]. Beijing: University of Science and Technology of China, 2010. (in Chinese)
[5] 侯雪.基于comsol的肺部电阻抗断层成像仿真研究[D]. 天津:天津大学, 2011. Hou Xue. Lung electrical impedance tomography simulation based on COMSOL[D]. Tianjin: Tianjin University, 2011. (in Chinese)
[6] 李忠良.基于压电阻抗健康监测的实验及有限元仿真分析[D]. 浙江:浙江大学,2013. Li Zhongliang. Experimental and numerical simulation of health monitoring based on EMI[D]. Zhejiang: Zhejiang University, 2013. (in Chinese)
[7] 毛亚琴.电阻法研究碳纤维树脂基单向拉挤复合材料的破坏行为[D]. 北京:北京化工大学,2004. Mao Yaqin. Study on the failure behavior of cfrp unidirectional pultruded composites by electrical resistance method[D].Beijing: Beijing University of Chemical Technology, 2004. (in Chinese)
[8] 陈小燕.基于COMSOL软件的大地电磁正演模型[D]. 西安:长安大学,2014. Chen Xiaoyan. Magnetotelluric forward modeling based on software of COMSOL[D]. Xi’an: Chang’an University, 2014. (in Chinese)
[9] Feng Zhongkui, Xu Ying, Li Xian, et al. Optimum electromagnetism design based on co-simulation of Matlab and COMSOL[J]. Electromagnetic Analysis and Applications, 2012, 01(01): 13-17.
[10] 许灿荣.基于COMSOL的近距离下保护层开采瓦斯流动模型[D]. 河南:河南理工大学,2012. Xu Canrong. Methane flow model of the near distance lower protective coal seam based on COMSOL[D]. Henan: Henan Polytechnic University, 2012. (in Chinese)
■
STUDY ON THE RESISTANCE BETWEEN ENDPOINTS IN DIAMETER OF A THIN DISC CONDUCTOR
Wang Lan1Xi Xiaoqiang2
(1School of Science;2Institute of Internet of Things and IT-based Industrialization, Xi’an University of Posts and Telecommunications, Xi’an Shaanxi 710061)
It was difficult to apply immediate integral to measure the resistance of thin disc conductor. In order to solve this problem, this paper studied the method for measuring the resistance of thin disc by finite element method. Firstly, the measurement platform of thin disc resistance was designed by Comsol multiphysics software. Based on this design of electrode, we studied the relationship between the thin disc resistance and the disc radius, the electrode position, the position and size of the small hole on the thin disc. Then, resistance of thin disc could be measured indirectly by the disc resistance expression, which was fitted by the least square method. Finally, the above measurement method for the resistance of thin disc was verified with immediate integral under the typical condition, and the results show that the error of the method was quite small. This paper was of great significance for the design of resistance of thin disc. In addition, the resistance measurement method could also be promoted the design of resistance of other shapes.
thin disc conductor; resistance; Comsol multiphysics
2016-04-27;
2017-03-10
国家自然科学基金(11275099;11475135)。
王岚,女,硕士研究生,研究方向为物理方法在信息处理中的应用,563859805@qq.com。
王岚,惠小强. 薄圆盘直径端点之间电阻的研究[J]. 物理与工程,2017,27(4):37-41.
