狭义相对论教学中不该出现的错误

张元仲

(中国科学院理论物理研究所，北京 100190)

特约稿件

狭义相对论教学中不该出现的错误

张元仲

(中国科学院理论物理研究所，北京 100190)

本文为了阐明个别大学物理教材中对光速不变假设的错误评论而详细说明了光速不变原理的两个用途：首要用途是用来定义惯性系中的时间坐标(即定义同时性)；第二个用途是用来推导洛伦兹变换。随后，在分析了钟慢效应、尺缩效应、同时性的相对性之后解释了尺缩佯谬，并特别指出了某大学物理教材中对一道习题提供的答案是错误的并用两种解法给出了正确答案。

光速不变原理；相对性原理；洛伦兹变换；时钟变慢；尺子缩短；同时性的相对性

1 背景

爱因斯坦狭义相对论第一篇论文的第一节“同时性的定义”非常重要[1,2],而且我们在《物理与工程》期刊上发表的相关文章[3]也强调了这个问题；但是最近发现仍有个别大学物理教材中存在对狭义相对论的错误评述。例如：(1)在芶秉聪和胡海云主编的《大学物理 下册(2版)》[4]第144页评论道：“光速不变原理从属于爱因斯坦相对性原理，前者可由后者推出，后者才是狭义相对论的基本假设”，而且该书第242页给出的习题11-12的答案是错的。(2)在张三慧教授编著的《大学物理学·力学、热学》第257页的脚注中评论道[5]：“如果把光速当成一个‘物理规律’，则光速不变原理就成了相对性原理的一个推论，无需作为一条独立的假设提出。相对论理论不应是电磁学的一个分支，不应该依赖光速的极限性。可以在空间的均匀性和各向同性的‘基本假设’的基础上，根据相对性原理导出洛伦兹变换而建立相对论理论”；并给出了这一错误观点的源头[6]：Mermin N D, Relativity without light. Am J Phys, 1984, 52(2), 119～124。

对以上错误评述有必要进行澄清：谁都不能“without light”。

2 狭义相对论的两个基本原理(或假设)

2.1 狭义相对性原理

一切物理定律在所有惯性系中均有效。对比经典力学中的相对性原理：力学定律在所有惯性系中均有效。可以看出狭义相对性原理只是一种推广。在没有明确定义惯性系(特别是其中的同时性)之前就无法导出坐标变换，也就无法用坐标变换表述相对性原理。

2.2 光速不变原理

光在真空中总是以不变速度c传播且与光源的运动无关。

对于光速不变假设在狭义相对论中的地位，爱因斯坦早在1916年发表的《广义相对论基础》[1]一文中已经明确指出：“狭义相对论同经典力学的分歧不在于相对性原理，而只在于真空中光速不变的假设，这个假设和狭义相对性原理结合起来，如所周知，就得出了同时性的相对性和洛伦兹变换，……”。可是遗憾的是，100多年后的当代，一些作者竟然没有真正理解爱因斯坦这种评论的具体含义。

光速不变原理有两个用途：首要用途是“对钟”；第二个用途是推导洛伦兹变换。为了阐明这两种用途，下面将说明：(1)迄今为止人类用来“对钟”的唯一手段就是用光信号*要想使用一只移动的标准时钟去对准各地的时钟就要先知道移动的速度对于标准时钟速率的影响，但是没有办法确切知道这种影响。；(2)单向光速不能由实验测定而只能假定；(3)假定了单向光速不变后才能使它的数值取双程光速的实验测量值；(4)有了单向光速的数值才能被用来校准全空间各地的时钟从而才定义了惯性系的时间坐标t；(5)定义了时间坐标才能最终定义好惯性系，然后才有速度或其他与时间有关的物理量的测量。这就是爱因斯坦在他的第一篇狭义相对论的论文中的第一节陈述“同时性的定义”的原因。但是那些

“without light”的作者们在没有“对钟”的前提下就出现了速度之类的物理量。

3 最不能缺少的就是光速不变的假设

3.1 社会活动计时和实验测量离不开(单向)光速不变的假设

“对钟”是社会活动不能缺少的操作，否则就没有共同的时间概念，更无法测量物体的运动速度等等物理量。在我们使用手机、电脑、电视显示的时间数字来进行日常活动的“对钟”过程中忽略了电磁信号传到我们这里所花费的时间，因为这个时间差别对于日常活动来说太微小了；但是对于精密的实验测量，这个微小的时间差别就不能被忽略。此时严格的“对钟”过程是： 在A钟的tA时刻从A点发射的光信号到达B点的时间是t=tA+r/c(其中r是A到B的距离，c是真空中的单向光速)；因为tA时刻是任意的，为了简单，取tA=0。这样，光信号到达B所花费的时间就简化成

(1)

在B钟接收到这个信号时把它的时间调节到式(1)右边给出的数值，这就把B钟与A钟对准了。B点是空间的任意一点，所以这也就使得全空间各地的时钟互相对准了。迄今为止，自然界中存在的用来对钟的信号只有光信号(或者说电磁信号)；所以，最不能抛弃的就是“光”。需要强调的是：上面说的“对钟”跟坐标变换无关，因为我们只在同一个参考系统中进行操作。另一点需要强调的是，上述对钟需要事先知道单向光速c的具体数值才行。

但是，如下面第3.6节指出的，单向光速不能用实验测得，假定了单向光速不变后c就可以取双程光速的实验测量值。

3.2 使用没有事先对准的B钟和A钟测量物体的速度仍需要单向光速的数值

设一个“粒子”与一个“光信号”从A点在tA时刻同时起跑，光信号到达B点时B钟显示的时间是tL(因为B钟没有事先同A钟对准，所以tL与tA的差值即tL-tA没有任何物理意义)。“粒子”到达B时B钟显示的时间是tP(参见图1)；

图1 测量粒子由A到B所用的时间

垂直的实线是B点的时钟B显示的时间(由下至上B钟的读数由小到大)，水平虚线是光信号的路径，其到达B钟的时间是tL，上、下虚线是粒子的路径；上面的路径代表粒子速度小于光速的情况，下面的路径代表粒子速度大于光速的情况；它们跟光路径实际重合，但是为了区分它们而把它们分开划了——这相当于时空图，粒子到达B的时间是tP

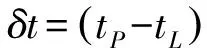
(2)

其中δt的取值范围是：

有3个极端的情况：

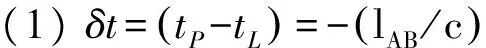
用式(2)计算粒子的速度u=lAB/ΔtAB必须事先知道光速c=30万km/s这个具体数值才行。

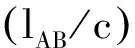
以上分析表明，不知道单向光速的数值就无法测量粒子运动的时间(因为B钟和A钟事先没有互相“对准”)因而也就无法给出粒子的速度。

3.3 惯性系的时间坐标定义离不开光速不变假设

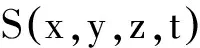
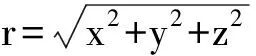
接下来，时间坐标t还需要定义(也就是需要同时性的定义)。点P(x,y,z,t)处的时间必须用放在该点的一只标准时钟给出。这只时钟显示的时间假定是均匀流逝的(这跟牛顿力学中的没区别)。但是，最重要的是各地的时钟在互相对准之前它们各自显示的时间只是“当地时间”。因此如上节所说，在没有对准的时钟之间来比对它们所显示的时间没有任何意义。只有把空间所有地方的时钟互相对准之后，那些时钟显示的时间才是惯性系的时间坐标t。上节已给出了使用光信号对钟的方程式(1)，式(1)的时间t就是惯性系的时间坐标。

3.4 回顾爱因斯坦原文中有关“对钟”的内容

爱因斯坦狭义相对论的第一篇论文[2]《论动体的电动力学》的第一节其标题就是“同时性的定义”。在此引用其中的重要陈述：“如果在空间的A点放一只钟，那么对于A附近的事件的时间，在A处的一个观察者能够通过找出与这些事件同时出现的时针位置来加以测定。如果又在空间的B点放一只钟——我们还要加一句话，‘这是一只同放在A处的钟完全一样的钟’——那么，通过在B处的观察者也能够求出B附近的事件的时间来。但要是没有进一步的规定，就不可能把A处的事件同B处的事件在时间上作比较。到此为止，我们只定义了一个‘A时间’和一个‘B时间’，但还没有定义对于A和B是公共的‘时间’。然而，当我们通过定义光从A到B所需要的‘时间’等于它从B到A所需‘时间’的时候，这后一个时间也就可以定义了。……那么放在A处和B处的这两只钟按照定义就是同步的。……这样，我们借助于某些(想象的)物理经验，对于静止在不同地方的各只钟，规定了什么叫做它们走得同步，从而显然也获得了‘同时’和‘时间’的定义。”

爱因斯坦的这一节即同时性的定义(或说时钟同步)是讨论与时间有关的一切物理量的前提，而这些量中最常见的就是速度的定义与测量。不使用不变的光速来定义惯性系就谈不上什么叫速度，也谈不上洛伦兹变换的推导问题，也就无法建立狭义相对论。所以用光速不变原理“对钟”是狭义相对论的首要任务*那些“without light ”的作者们要么没有阅读过爱因斯坦狭义相对论原著中的这一小节，要么就没看懂爱因斯坦为什么把“同时性的定义”放在文章的首位。。

3.5 单向光速不能用实验测定而只能假定

原则上说单向光速不可能用实验进行测定，或者说单向光速是否各向同性不可能用实验进行检验。

一个质点的速度v=lAB/tAB，也就是A和B两点之间的距离lAB除以时间间隔tAB=tB-tA，而时间tA是质点通过A时由那里的A钟测定的时间，tB是质点通过B时由那里的B钟测定的时间，钟A和钟B不在同一个地点，前面说过只有它们事先用光信号对准之后它们的时间差才能代表质点从A点运动到B点所用的时间。

如果把上述质点换成光信号，就陷入了逻辑循环：要测量光速就要先把A钟和B钟对准，要把A钟和B钟对准又要先知道光速的数值。所以说迄今为止单向光速的数值是不可能用实验直接给出的。

单向光速不能被实验给出，也就是说光在不同方向的传播速度是否相同不能用实验判断。这一点彭加勒早在1905年之前就已经指出了。他在1898年发表的“时间测量”的论文中写道：“光具有不变的速度，尤其是它的速度在一切方向上都是相同的，这是一个公设，没有这个公设，就无法量度光速。这个公设从来也不能直接用经验来验证；……。” 所以爱因斯坦在狭义相对论的第一篇论文中对单向光速的不变性只能假定。

3.6 为何必须假设单向(单程)光速不变

(3)

其中，

(4)

这里的tB是光到达B点由那里的B钟记录的时间。式(4)代入式(3)后给出

(5)

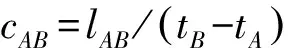
(6)

4 关于狭义相对性原理(简称相对性原理)

相对性原理是说一切物理定律在所有惯性系中均有效。

应用这个原理的前提是先定义好惯性系的空间坐标和时间坐标，上一节已经对时间坐标的定义作了具体说明，而在定义时间坐标时只需要单向光速不变的假定而不需要相对性原理。

惯性系就是惯性定律成立的那种参考系。定义了空间坐标和时间坐标后才能有惯性定律的如下陈述：不受力的质点要么相对静止要么匀速直线运动(因为定义了空间坐标才有直线的定义，而定义了时间坐标才能有匀速运动的定义)。在没有坐标变换的情况下，相对性原理无法用坐标变换来表述。

5 洛伦兹变换的推导

狭义相对论只在惯性系中有效，所以定义惯性系是其首要任务。惯性系中的时间坐标t使用式(1)定义：

(7)

取平方后变成

x2+y2+z2-c2t2=0

(8)

(9)

(10)

这里假定了各个惯性系中的光速不变*文献[5]第257页的脚注中说：“如果把光速当成一个‘物理规律’，则光速不变原理就成了相对性原理的一个推论，无需作为一条独立的假设提出。”但是这种说法是完全错误的；上面已经反复强调没有光速不变的假设就不能“对钟”也就没有速度的定义和惯性系时间坐标的定义。而且，就是按照相对性原理，式(9)和式(10)中的c应当写成c′，要使c′=c只能假定而不可能是相对性原理的推论。况且，在同一个惯性系中相对性原理根本就无法推论出光速与方向无关。需要强调：式(8)和式(10)只是光的运动学而不涉及光的动力学(‘物理规律’)。

设S系和S′系具有特殊的初始状态：S′系相对于S系沿其x的正向以不变速度v运动，且在初始时刻两系统相互重合。根据相对性原理，在S系作匀速直线运动的质点在S′系看来也是匀速直线运动，那么这两个惯性系之间的坐标变换(最简单的形式)是如下的线性变换(为了简单,略去垂直方向的坐标变换y′=y,z′=z)：

(11)

确定其中的3个常数α,β,γ最简单方便的方式就是使用光速不变原理的方程式(8)和式(10)，因为这两个方程先前已经被用来定义惯性系的时间坐标。将式(11)代入式(10)后需要变成式(8)，即坐标变换要保证光速不变。由此解出α,β,γ后式(11)就成为通常熟悉的洛伦兹变换(略去了y′=y,z′=z)：

(12)

因为洛伦兹变换是线性变换，所以时空间隔的洛伦兹变换形式不变(同样略去了Δy′=Δy,Δz′=Δz)：

(13)

其逆变换是：

(14)

6 再谈狭义相对性原理

有了洛伦兹变换式(12)之后，狭义相对性原理才能更具体地陈述为：一切物理定律的方程式在洛伦兹变换下保持形式不变。

相对性原理的这种表述为我们提供了构造近代物理理论的具体方法： 首先使用物理系统的动力学变量构造出在洛伦兹变换下不变的作用量，然后取作用量对动力学变量的变分等于零(最小作用量原理)即得到该物理系统的动力学方程(欧拉-拉格朗日方程)，这样得到的方程在洛伦兹变换下保持形式不变(即满足狭义相对性原理的要求)。例如，平直时空的宏观理论有：(狭义)相对论力学、运动介质的(狭义)相对论电磁学等；微观理论有：(狭义)相对论量子力学、(狭义)相对论性的量子电动力学、(狭义)相对论性的粒子物理理论等。所有这些(宏观的和微观的)理论其动力学方程式都在洛伦兹变换下保持形式不变；而且，这些作用量的洛伦兹不变性给出角动量守恒定律；时间坐标的平移不变性给出能量守恒定律；空间坐标的平移不变性给出动量守恒定律。所以说狭义相对论是所有这些近代物理理论的一大支柱。广义相对论在弯曲时空的局部具有洛伦兹不变性，即狭义相对论也是广义相对论的支柱；因而可以说广义相对论是(局部)狭义相对论性的引力理论。

7 钟慢效应

考虑静止在S′系中x′轴上的一只时钟其空间坐标间隔Δx′=0(即固定在一点不动)，代入洛伦兹变换式(14)得到：

(15)

把其中第二个式子写成：

(16)

这就是通常的钟慢效应；需要强调的是，Δt′是静止在S′系中的同一只时钟给出的时间间隔，因而是固有时间隔(是直接测量量，不涉及同时性定义)；而右边的Δt是由式(15)中的第一式给出的相距Δx>0的两只时钟记录的时间差，因而是坐标时间隔(与同时性定义相关)；所以，式(16)是说(因为两个惯性系的相对速度v总是小于真空光速c所以右边的根号小于1)：一只运动的时钟其速率比两只异地的时钟读数之差慢了(固有时间隔比坐标时间隔小)。

8 尺缩效应

(17)

(18)

式(17)就是尺缩公式，表明运动尺子的长度l比静止长度(固有长度)l0短了。

9 同时性的相对性

(19)

其中用到了式(18)和式(17)；这个结果在后面解题中会用到。这个结果说明：在S系的不同地点同时(Δt=0)发生的两个事件在S′系看来不是同时(Δt′≠0)发生的，这就是“同时性的相对性”。

10 尺缩佯谬

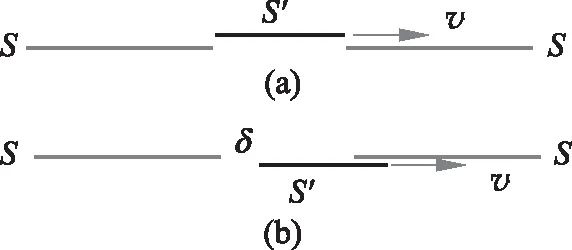
图2 尺缩佯谬

参见图2(灰色部分是桌面，黑色部分是杆子)：一根杆子静止时跟桌面的沟槽长度相同，如果它以速度v在桌面上移动，在运动到图2(a)的位置时在桌面的S系同时(Δt=0)按下它的前后两端，按照尺缩的公式(17)在S系的运动长度l比静止桌面上的沟槽长度l0短因而可以掉入沟槽；但是在随杆子运动的S′系看来沟槽在向相反的方向移动因而沟槽缩短所以杆子不能掉入沟槽(尺缩佯谬)。解决这个假矛盾的关键是注意到同时性的相对性：对于在桌面(S系)同时(Δt=0)按下杆子的前后两端这个操作，在杆子系(S′系)看来是先按下它的前端之后，过了Δt′的时间才按下他的后端，而此时沟槽已经向杆子后端运动了式(19)给出的δ距离(参见图2(b))，这时杆子的后端已经进入到沟槽内的位置，所以在S′系看来杆子的前端先进入沟槽，杆子的后端后进入沟槽(当然在忽略桌面厚度的情况下杆子是“钻入”沟槽的)。

11 《大学物理 下册(2版)》[4] 第166页习题11-12

为了后面解题用语方便我们把原文中的“粒子”换成了“时钟”。原题如下：

两个时钟A,B以0.6c的相对速度互相接近，如果A所在参考系的观测者测得两钟距离为3×108m时，B所在参考系的观察者测得两钟还要经过多长时间碰撞？

该书第242页给出的答案2.08s是错的。这个错误答案的解法是由《大学物理—学习指导与习题解答.2版》[7]第179页给出的。

正确的解答可以有如下两种等价的解法：

解法1 “钟慢”效应：

在A系看来B钟距离A钟为l=3×108m，所以B钟以速度v=0.6c与A钟相遇所用时间为

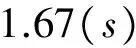
(20)

而运动的时钟B记录的时间间隔ΔτB由钟慢效应式(16)给出：

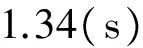
(21)

所以答案是：B所在参考系的观察者测得两钟要经过1.34s而相遇。

解法2 “尺缩+同时性的相对性”效应：

两只钟的距离l=3×108m是A系测量运动的A跟B之间的距离，按照尺缩公式(17)B系中的相应的固有距离是

(22)

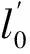
因而，在B看来A运动到B的时间间隔(由B钟记录的时间间隔)是

(24)

其中第二个等号用了式(20)。这个结果与解法1.给出的钟慢结果式(21)相同。

12 后记

1) 在开头“背景”中引述的“without light”的观点来源于一个美国教授(Mermin N D)在美国的与教学有关的刊物《美国物理学杂志(American Journal of Physics)》上发表的文章[6]。这种错误观点竟然被我们的个别《大学物理》之类的与教学有关的教材和参考书中引用。试想，如果这类文章是由一个中国教授撰写的并发表在中国的物理学杂志上，这些《大学物理》之类的书籍还会全盘采纳吗？

2) 感谢在撰写本文的过程中北京工业大学王雯宇老师、《物理与工程》编辑部主任钱飒飒和编辑刘洋给予的大力帮助。

[1] 爱因斯坦，广义相对论基础[J]，德国《物理学记事》第四系列，1916,49: 769-822(中译文见上海人民出版社1973年出版的《爱因斯坦论著选编》第36页)

[2] 爱因斯坦，论动体的电动力学[J]，德国《物理学记事》第四系列，1905,17:891-921(中译文见上海人民出版社1973年出版的《爱因斯坦论著选编》第1-22页)

[3] 张元仲.爱因斯坦建立狭义相对论的关键一步——同时性定义[J].物理与工程，2015，25(3): 3-8. Zhang Yuanzhong. A key step in the development of the special relativity by Einstein-Definition of simultaneity[J]. Physics and Engineering, 2015, 25(3): 3-8.(in Chinese)

[4] 芶秉聪,胡海云.大学物理 下册[M].2版.北京：国防工业出版社，2015年1月：144，242.

[5] 张三慧.大学物理学-力学、热学[M].3版.第257页，北京：清华大学出版社，2008.

[6] Mermin N D. Relativity without light[J]. Am J Phys, 1984, 52(2): 119-124.

[7] 芶秉聪,胡海云.大学物理—学习指导与习题解答[M].2版.北京：国防工业出版社，2013:179.

■

THE MISTAKES THAT SHOULD NOT APPEAR IN THE TEACHING MATERIALS OF SPECIAL RELATIVITY

Zhang Yuanzhong

(Institute of Theoretical Physics, Chinese Academy of Sciences，Beijing, 100190)

In order to clarify the wrong comments on the light speed invariance hypothesis in some of the teaching materials of “University Physics”, this paper illustrates in detail the two purposes of the light speed invariance principle: Its primary purpose is used to define the time coordinates in an inertial frame (i.e., defining simultaneity); The second purpose is used to derive the Lorentz transformation. After analyzing the time dilation effect, the length contraction effect and the relativity of simultaneity, we then explain the length contraction paradox. Finally we point out that the answer of an exercise providing in a book of “University Physics” is wrong, and we give the correct answer by use of two methods.

light speed invariance principle; the principle of relativity; Lorentz transformation; time dilation; length contraction; relativity of simultaneity

2016-04-19

中国科学院战略性先导科技专项(B类)资助，任务编号XDB23030100和XDB21010100；国家自然科学基金No 91436107。

张元仲，男，研究员，主要研究领域是相对论、引力物理与宇宙学，著有专著《狭义相对论实验基础》。

张元仲. 狭义相对论教学中不该出现的错误[J]. 物理与工程，2017，27(4)：3-9.