On algebraic convergence of non-elementary discrete subgroups of SL(2,Qp)

Yang Jinghua(College of Sciences,ShanghaiUniversity,Shanghai200444,China)

On algebraic convergence of non-elementary discrete subgroups of SL(2,Qp)

Yang Jinghua
(College of Sciences,ShanghaiUniversity,Shanghai200444,China)

In the Kelinian groups,the study ofthe algebraic convergence ofthe sequence ofthe discrete subgroups is a very importanttopic,since the algebraic convergence of the sequence ofthe discrete subgroups can be applied to study the deformations the manifolds and the Hausdorffdimension of the limit sets of the discrete subgroups.With the rapid developments of the p-adic Lie groups and the algebraic dynamicalsystems,itis very importantto study the topics of algebraic convergence of the p-adic discrete subgroups.In this paper,we discuss the algebraic convergence ofa sequence{Gn,r}ofr-generator non-elementary discretesubgroups of PSL(2,Qp)by use of the Jorgensen inequalities in PSL(2,Qp) and the subgroups of PSL(2,Qp)acting isometrically on the hyperbolic Berkovich space.We prove thata sequence{Gn,r}ofr-generatornon-elementary discretesubgroups of PSL(2,Qp)converges to a non-elementary discrete subgroup of PSL(2,Qp)algebraically.

p-adic Mobius maps;algebraic convergence;discrete subgroups

2010 MSC:51B10,32P05,37P05,40A05

1 Introduction

Let Cpbe the completion of the algebraic closure of Qp,where Qpis the field of p-adic rational numbers. For Cp,the projective space(Cp)=Cp∪{∞}is totally disconnected and not locally compact.The Berkovich projective spaceis a compactaugmentation of P1(Cp)and is also a uniquely path-connected Hausdorff space which contains P1(Cp)asitsdense subset.By Berkovich’sclassification theorem,pointsofrP1(Cp)correspond to discs D(a,r)⊂Cp,orto nested sequences ofdiscs.The pointζGcorresponding to D(0,1)is called the Gauss point.The elementin the projective speciallinear group PSL(2,Cp)is called the p-adic M¨obius map.The action ofthe p-adic M¨obiusmap on P1(Cp)continuously extendsto an isometricalmap on the hyperbolic Berkovich space HBer=P1(Cp).Forthe foundation,see[1–3],more details can be found in section 2.

Consider a sequence of subgroups{Gn,i}generated by r p-adic M¨obius maps,say gn,1,···,gn,r.If for each k∈{1,···,r},the sequence gn,kconverges to a p-adic M¨obius maps gkthen one says that{Gn,i}converges algebraically to the group G generated by g1,···,gr,or G is the algebraic limitofthe sequence{Gn,i}.

There are many discussions of algebraic convergence of Kleinian groups;see[4–6].With the developmentof studying the arithmeticaldynamics,itis an importanttopic in the theory of p-adic M¨obius maps in non-archimedean spaces(see[3,7–11]).However,it is also an open question in the arithmetical settings to study the algebraic convergence of discrete subgroups of PSL(2,Qp).Hence we give a clear picture of it.

Theorem 1 Letthe sequence ofnon-elementary discrete groups{Gn}of r−generatorsconvergesto the group G.Then the group G is also non-elementary discrete.

2 Some basic facts

Let p≥2 be a prime number.Let Qpbe the field of p-adic numbers and Cpbe the completion of the algebraic closure of Qp.Denote|C∗p|the valuation group of Cp.Then every element r∈|C∗p|can be expressed as r=pswith s∈Q.The absolute value satisfies the strong triangle inequality

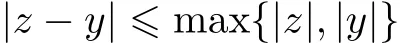
for x,y∈Cp.If x,y and z are points of Cpwith|x−y|＜|x−z|,then|x−z|=|y−z|.

Given a∈Cp,and r＞0,the open and closed disks with center at a with radius r are defined by

However,by the strong triangle inequality,topologically D(a,r)−and D(a,r)are closed and open,and every pointin disk D(a,r)−is the center.This implies thatif x∈D(a,r)−,then D(a,r)−=D(x,r)−(resp.D(a,r)= D(x,r)).iftwo disks D1and D2in Cphave non-empty intersection,then D1⊂D2,or D2⊂D1.Fora set E⊂Cp, denote diam(E)=|z−w|the diameterof E in the non-Archimedean metric.Especially,diam(D(a,r))=r.

Let P1(Cp)be the projective space over Cpwhich can be viewed as P1(Cp)=Cp∪{∞}.The chordaldistance on P1(Cp)can be defined by

In[8],Kato introduced the method thatwas used in Kleinian groupsto study the discrete subgroupsof PSL(2,Cp). He classified non-unitelements g in PSL(2,Cp)into the following three classes:

(a)g is said to be parabolic ifithas only one eigenvalue.

(b)g is said to be elliptic ifithas two distincteigenvaluesλ1andλ2with|λ1|=|λ2|.

(c)g is said to be hyperbolic ifithas two eigenvaluesλ1andλ2with|λ1|/=|λ2|.

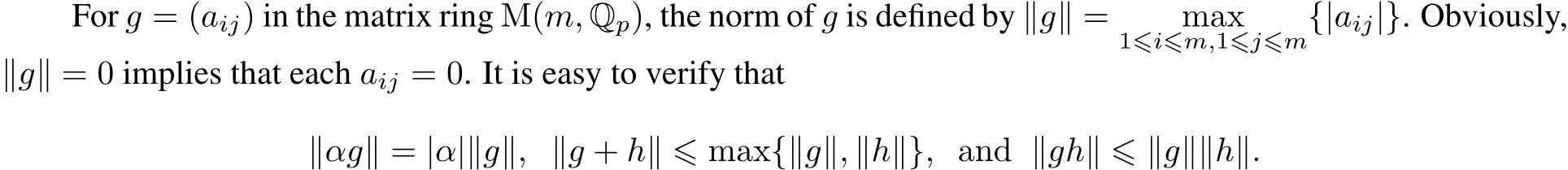
We say that a subgroup G of SL(m,Qp)is discrete if there existsδ=δ(G)＞0 such that each element g∈G{I}satisfies‖g−I‖＞δ,where I denotesthe unitelement.

Obviously,a subgroup G of SL(2,Qp)is discrete if and only if any sequence consisting of distinctelements gn∈G isnota Cauchy sequence.Since≤‖h−1‖‖gn−g‖‖h‖,we have‖−→0,when gn−→g,as n−→∞.This means thatconjugation does notchange the discreteness.

We say that G is elementary if there exists a finite G−orbit inand G acts discontinuously on HBerif for any sequence,the sequencehas no convergentsubsequence in HBerfor any point x∈HBerwith respectto the Berkovich topology.

Lemma 1[3]Ifa discrete subgroup G of PSL(2,Cp)is elementary,then either G is conjugate to a subgroup of PSL(2,Cp),every elementofwhich leaves{0,∞}invariantand is therefore ofthe formzs,a/=0,s2=1, oreach elementin G shares the same fixed pointin HBer.

Lemma 2[8]Let G be a discrete subgroup of SL(m,Qp).Then

(1)there is no parabolic elementin G;

(2)there is no elliptic elementof infinite order in G.

Lemma 3[12]The subgroup G of SL(m,Qp)is discrete if and only if any cyclic subgroup of G is discrete.

Lemma 4[11]If a discrete subgroup G of SL(2,Qp)contains elliptic elements only,then G is a finite group.

Lemma 5[12]Ifa subgroup G of SL(2,Cp)is discrete,then foreach g∈G{I},‖g−I‖≥p

3 Algebraic convergence of non-elementary discrete subgroups

Lemma 6 Let

with gh=hg−1.Then g commutate with h.

Proof Since

we see thateitherλ2=−1,namely h=−z,orifλ2/=±1,we have b=c=0,a=d namely g(z)=I.Hence g commutate with h.

Proof[Proofofthe Theorem 1.]Since each Gnis discrete,we see thatforany I/=g∈Gn,‖g−I‖≥If the sequence gn∈Gnconverges to g∈G,by ultrametric properties,we know that‖g−I‖≥.Hence by Theorem 4,we see that G is discrete.

We claim that G is non-elementary.Suppose that G is elementary.By Theorem 1,either G is conjugate to a subgroup of PSL(2,Cp),every elementof which leaves{0,∞}invariantand is therefore of the form z−→azs, a/=0,s2=1,or G contains elliptic elements only.

If G contains elliptic elements only,then G is finite.Since each Gnis of r−generators and infinite,there exist two sequence{hn,1}and{hn,2}converging to the same element h,namely hn,1◦tending to I.By ultrametric properties,we see that hn,1=hn,2,since Gnis discrete.This implies that G is infinite,namely G contains a loxodromic elementatleast.

If G contains elements leaving two points invariant,letting H be the union of allthe finite extensions ofof degree 2.Then each elementin G is ofthe form z−→0/=a∈H,s2=1.

Firstcase,let

tend to A2z and B2z.Since

we see that[gn,1,gn,2]tends to A4I.Since Gnis discrete,we know thatg=I,namel=.By Lemma 6,we see that gn,1commutate with gn,2.

In the end,since gn,1and gn,2are chosen arbitrarily,we see that each generator commutate with each other which implies that Gnis an elementary group.This is a contradiction.

[1]RobertA M.A course in p-adic analysis[M].New York:Springer-Verlag,2000.

[2]Baker M,Rumely R.Potential theory and dynamics on the Berkovich projective line[M].Providence,RI:American Mathematical Society,2010.

[3]Qiu WY,Yang JH.On limitsets ofdiscontinuous subgroups ofthe Berkovich space.preprint.

[4]Jørgensen T.On discrete groups of M¨obius transformations[J].Amer JMath,1976,98:739-749.

[5]Jørgensen T,Klein P.Algebraic convergence of finitely generated Kleinian groups[J].Quart J Math Oxford,1982, 33(2):325-332.

[6]Yang S H.Algebraic convergence of finitely generated Kleinian groups in all dimensions[J].Linear Algebra and Its Applications,2010,432(5):1147-1151.

[7]Armitage JV,Parker JR.Jørgensen’s inequality fornon-archimedean metric spaces[J].Geometry and Dynamics of Groups and Spaces,2008,265:97-111.

[8]Kato F.Non-archimedean orbifolds covered by Mumford curves[J].Journalof Algebraic Geometry,2005,14:1-34.

[9]Qiu WY,Wang Y F,Yang JH,etal.On metric properties oflimitsets of contractive analytic non-Archimedean dynamical systems[J].JMath Anal Appl,2014,414:386-401.

[10]Wang Y F,Yang J H.The pointwise convergence of the p-adic M¨obius maps[J].SciChina Math,2014,57(1):1-8.

[11]Wang Y F,Yang JH.On p-adic M¨obius maps[J/OL].preprintarXiv:1512.01305.

[12]Qiu W Y,Yang J H,Yin Y C.The Discrete subgroups and Jørgensen’s inequality for SL(m,Cp)[J].Acta Math Sin (English Series),2013,29(3):417-428.

O 174.51 Document code:A Article ID:1000-5137(2017)03-0358-05

10.3969/J.ISSN.100-5137.2017.03.003

date:2016-09-20

This research was supported by Natural Science Foundation of China(11301510,11671092).

Yang Jinghua,professor,reseach area:algebraic dynamical system.E-mail:davidyoung@amss. ac.cn