Comments on new iterative methods for solving linear systems

Wang Ke,Tan Lijun,Wang Shiheng(.College of Sciences,Shanghai University,Shanghai200444,China; 2.Departmentof Basic Education,Nanyang Vocational College of Agriculture,Nanyang 473000,China)

Comments on new iterative methods for solving linear systems

Wang Ke1,Tan Lijun1,Wang Shiheng2∗
(1.College of Sciences,Shanghai University,Shanghai200444,China; 2.Departmentof Basic Education,Nanyang Vocational College of Agriculture,Nanyang 473000,China)

Some new iterative methods were presented by Du,Zheng and Wang for solving linear systems in[3],where it is shown that the new methods,comparing to the classical Jacobi or Gauss-Seidel method,can be applied to more systems and have faster convergence.This note shows that theirmethodsare suitable formore matrices than positive matriceswhich the authorssuggested through furtheranalysis and numericalexamples.

iterative method;linear system;classicaliteration

2000 MSC:15A06,65F10

The nonsingularlinearsystem

where A=(aij)∈Rn×n,x∈Rnand b∈Rn,has many applications in scientific computing[1−2].In[3],Du, Zheng and Wang discussed some new iterative methods for solving(1).This note will show that their methods are suitable formatrices otherthan positive matrices.

For(1),Du,Zheng and Wang[3]proposed the following two iterative schemes(2)and(3),

and E2=−(A−D2).

The convergence theorems for(2)and(3)are as below.

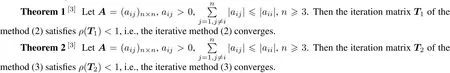
For Theorem 1,they addressed the following remarks.

Remark 1[3]1.The size n ofthe matrix A has to satisfy n≥3.Forinstance,let

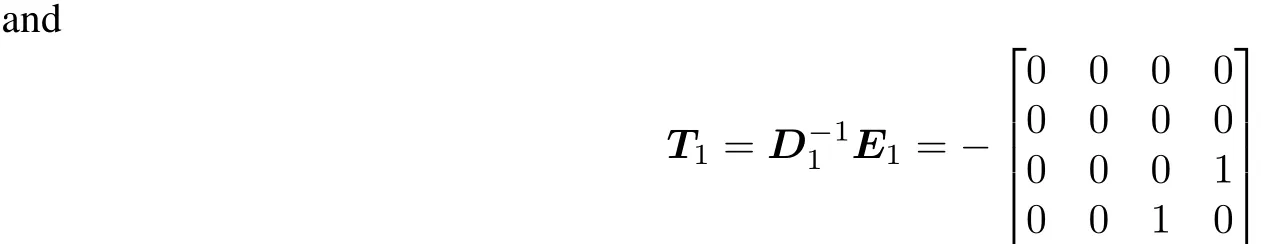
whose eigenvalues are 0,0,1 and−1.Soρ(T1)=1.

3.Notice thatthe iterative method(2)convergeseven ifthe matrix A is justdiagonally dominant.

对照组的56例患者实施常规护理,常规护理的基本内容包括以下几点:一是护理人员要协助患者进行指甲修理,避免患者把皮肤抓伤,并多采用热肥皂水对皮肤患处进行烫洗;二是对患者实施用药指导时,护理人员要对患者病情的发展变化情况进行观察,并了解患者是否对正在服用的药物过敏,一旦发现异常情况时,要立即报告给主治医生,并及时给予处理;三是及时更换患者的脏衣物和床单,叮嘱患者保持皮肤的干燥清洁;四是对患者实施饮食干预,禁止患者进食生冷、辛辣等刺激性食物和海鲜类、菌类食物。

In fact,the firsttwo of Remark 1 are notnecessary.For the firstone,assume A=,then

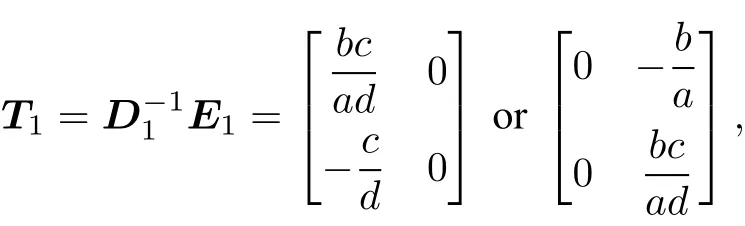
soρ(T1)=＜1 as|bc|≤|ad|and the equivalence does not hold with A nonsingular.What the authors addressed is only the case where A is singular.

As for the second one,it’s the same.The authors just presented an example with a singular coefficient matrix A.

The following examples illustrate the effectiveness of the new methods(2)and(3)to diagonally dominant matrices with zero and/or negative entries,compared with the classical Jacobi and Gauss-Seideliterative methods. The initialguess is 0 and the stopping criterion is

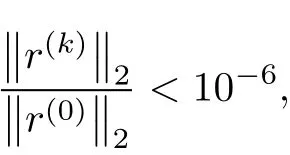
where r(k)is the residualvector after k iterations.The numericalresults are listed in Tables 1-3,where Jacobi,GS, Iand IIstand for Jacobimethod,Gauss-Seidelmethod,methods(2)and(3),respectively.

Example 1 Consider the n×n linear system(1)with

Table 1 Iterations(IT),CPU time(t)and relative error(ERR)for Example 1

Table 1 shows thatthe new iterative methods(2)and(3)are much betterthan Jacobiand Gauss-Seidelmethods. For alliterations,CPU times and precisions of methods(2)and(3)are the same.

Example 2 Consider the n×n dense linear system(1)with

Table 2 Iterations(IT),CPU time(t)and relative error(ERR)for Example 2

In this example,the new iterative method(2)has less iterations and CPU time than Jacobi method,and has less CPU time than Gauss-Seidelmethod;the method(3)is as good as Jacobimethod and better than Gauss-Seidel method.

Example 3 Consider the n×n dense linear system(1)with

and b=(1,2,···,n)T.

Table 3 Iterations(IT),CPU time(t)and relative error(ERR)for Example 3

In Table 3,the method(2)has less CPU time than Jacobiand Gauss-Seidelmethods.The method(3)has less both iterations and CPU time than Jacobiand Gauss-Seidelmethods.

[1]Varga R.Matrix iterative analysis[M].New Jersey:Prentice-Hall,Englewood Cliffs,1962.

[2]Young D.Iterative solution of large linear systems[M].New York:Academic Press,1971.

[3]Du J,Zheng B,Wang L.New iterative methods for solving linear systems[J].Journalof Applied Analysis and Computation,2011,1:351-360.

O 241.6 Document code:A Article ID:1000-5137(2017)03-0406-04

10.3969/J.ISSN.100-5137.2017.03.008

date:2016-10-19

This research was supported by NationalNaturalScience Foundation of China(11301330);grants of“The First-class Discipline of Universities in Shanghai”and Gaoyuan Discipline of Shanghai.

∗Corresponding author:Wang Shiheng,associate professor,reseach area:advanced algebra.E-mail:77917092@qq.com