Approximate controllability of semilinear fractional evolution equations of order α (1, 2] with finite delay

Ma Saisai,Kou Chunhai∗,Ge Fudong(.College of Science,Donghua University,Shanghai060,China;.College of Information Science and Technology,Donghua University,Shanghai060,China)

Approximate controllability of semilinear fractional evolution equations of order α (1, 2] with finite delay

Ma Saisai1,Kou Chunhai1∗,Ge Fudong2
(1.College of Science,Donghua University,Shanghai201620,China;
2.College of Information Science and Technology,Donghua University,Shanghai201620,China)

This paperconsiders the approximate controllability ofsemilinearfractionalevolution equations of orderα∈(1,2]with finite delay.Using the contraction mapping principle,we explore the existence and uniqueness of the mild solution.Furthermore,under certain hypotheses,the approximate controllability is obtained by the theory of strongly continuousα-order cosine family.As an illustration ofthe application ofthe obtained result,an example is given atlast.

approximate controllability;fractionalevolution equation;finite delay;α-ordercosine

2010 MSC:34A08,47D09,93B05

1 Introduction

In the pastfew decades,fractionaldifferentialsystems have played an importantrole in physics,chemistry and engineering,etc..Regarded asthe generalization ofintegerordersystems,fractionalordersystems are more suitablefor many experimentalresults thatthe integer order differentialsystems can’tdescribe[1−3].There exists numerous anomalous diffusion phenomena in real life.In order to model these phenomena accurately,fractional evolution equations are established by introducing the fractionaldifferentialoperator in the standard diffusion systems.Many researchersstudied the fundamentalissues offractionalevolution equations and many valuable results were obtained. For example,El-Borai[4]investigated the existence of the solutions of fractional evolution equations by using the Laplace transform.Balachandran and Park[5]considered the existence of the mild solutions of a class of nonlocal Cauchy problem for abstractfractionalsemilinear evolution equations by using fractionalcalculus theory and the fixed pointtheorem.Zhou and Jiao[6−7]discussed the existence of the mild solutions to fractionalevolution and neutralevolution equationsin a Banach space in which the mild solutionsare introduced based on probability density function and semigroup.The existence of mild solutions of fractionalevolution equations is the foundation for the research ofotherproperties ofthe related systems.

Moreover,we note that the study of controllability is essential for many engineering and physics problems. There are a lot of research works on the exact controllability and approximate controllability.But,the concept of exact controllability is too strong and the approximate controllability is more appropriate for practical application. There are many results on the controllability of fractional evolution equations of orderα∈(0,1],see[8–12].In these papers,the approximate controllability of semilinear fractionalevolution equations of orderα∈(0,1],with or withoutdelay,were studied.But,to the bestof our knowledge,the contributions on the controllability of semilinear fractionalevolution equations of orderα∈(1,2]are few.In[13–15],Lietal.studied the controllability of diverse fractional systems of orderα∈(1,2]by using fixed point theorem and operator theory.And Shukla et al.[16]investigated the approximate controllability of semilinear fractionalcontrolsystem of orderα∈(1,2]with infinite delay by sequence method.

Motivated by the abovediscussion,in thispaperwe study the approximate controllability fora classoffractional systemsoforderα∈(1,2]with finite delay in Banach space.Undera weak Lipschitz condition,some sufficientconditions are obtained to guarantee the approximate controllability of the systems.Considerthe following semilinear fractionalevolution equation

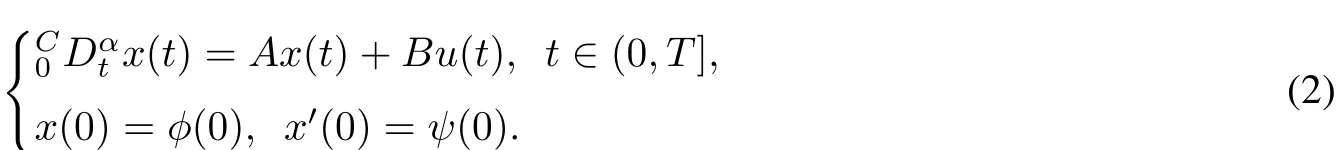
This paper is organized as follows.In section 2,we recallsome necessary concepts and give the definition of the mild solution of the system(1).Then the existence of the mild solution and the approximate controllability of the semilinear fractionalcontrolsystems are discussed in section 3.In section 4,we give an example to illustrate the effectiveness of our result.

2 Prelim inaries

Let X be a Banach spacew ith norm‖·‖Xand L(X)be the space of all bounded linear operatorson X.Let Lp([0,T];X),1≤p＜∞,be the space of X-valued Bochner integrable function f:[0,T]→X w ith the norm

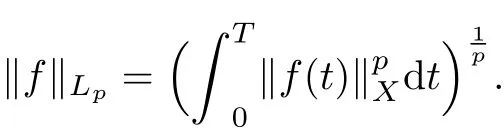
C([−h,0];X)and C([−h,T];X)are X-valued continuous functionalspacew ith thenorms

Cn([0,T];X)is the spaceof X-valued functionscontinuously differentiableat least to the nthorder.

In the follow ing,we recallsome definitions to beused throughoutthispaper.

Definition 1[2]The Riemann-Liouville fractional integral0Iαtx of orderα＞0 for a function x(·)∈L1([0,T];X)isdefined as

whereΓis the gamma function.

Definition 2[2]The Caputo fractional derivativex of orderα＞0 for a function x(·)∈L1([0,T];X)Cn([0,T];X)is defined as

where n=[α]+1.In particular,ifα∈(1,2),onehas

Follow ing[17],we have the follow ing definition.

Definition 3[17]A fam ily{Cα(t)}t≥0⊂L(X)is called the solution operator(or strongly continuousα-order fractionalcosine fam ily)for the system(3),if the follow ing conditionsare satisfied:

(a)Cα(t)is strongly continuous for t≥0 and Cα(0)=I;

(b)CαD(A)⊂D(A)and ACα(t)η=Cα(t)Aηforallη∈D(A),t≥0;

(c)Cα(t)ηisa solution of(3)forallη∈D(A).

A is called the infinitesimalgeneratorof Cα(t).

Definition 4[17]Theα-ordercosine family Cα(t)iscalled exponentiallybounded if thereareconstants M≥1 andω≥0 such that

If the solution operator Cα(t)of(3)satisfies(4),we shallsay A∈Cα(X;M,ω).

We define the corresponding fractionalsine family Sα:[0,∞)→L(X)by

and letthe associated fractional Riemann- Liou ville family be Pα:[0,∞)→L(X)such that

Taking the Laplace transform to(1),by the property of Laplace transform,we have

Definition 5[13,17]A function y(·)∈C([−h,T];X)is said to be a mild solution of the system(1)if y0= φ,=ψand

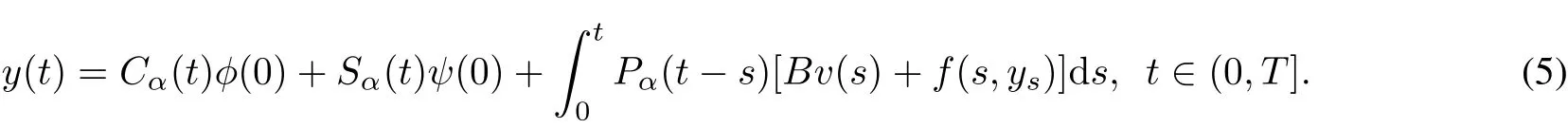
Let y(T;φ(0),ψ(0),v)be the state value of the system(1)attime T corresponding to the control v initialvalue φ(0).The system(1)is said to be approximately controllable in[0,T],if for every desired finalstate y1and constant∈＞0,there exists a controlfunction v∈L2([0,T],U)such that

Moreover,let KT(f)={y(T;φ(0),ψ(0),v);v∈U}.We see thatif=X,then the system(1)is approximately controllable,wheredenote the closure of KT(f).In particular,if=X,then the system(2)is approximately controllable.

3 Main Results

In this section,the existence of the mild solution and the approximate controllability for the system(1)are proved underthe following hypotheses:

•(H1)There exists a function l(·)∈Lβ1([0,T],[0,∞)),such that

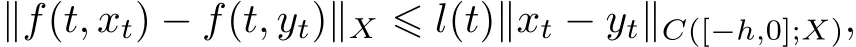
whereβ∈(0,1],xt(·),yt(·)∈C([−h,0],X),t∈[0,T]and l(t)≤N,for every t∈[0,T],N∈R+;

•(H2)The operator A belongs to Cα(X;M,0),i.e.,there exists a constant M≥1 such that‖Cα(t)‖X≤M,t∈[0,T];

•(H3)The operator B is invertible,and B−1:R(f)⊆X→U;

•(H4)Asλ→0+,λR(λ,ΛT)→0 in the strong operatortopology,where

and B∗(t)are the adjointoperators of B and Pα(t),respectively.

Similarto the argumentsin[8,18],we see thatthe hypothesis(H4)holdsifand only ifthe corresponding linear system(2)is approximately controllable on[0,T].

First,we prove the existence and uniqueness of mild solution of the system(1).

Theorem 1 Suppose that(H1)and(H2)hold.Then(5)admits a unique mild solution of the system(1)in C([−h,T];X)with y0=φ,=ψfor each controlfunction v(·)∈L2([0,T];U),provided that

Proof Define the mappingΦ:C([−h,T];X)→C([−h,T];X)as

Now,we proveΦhas a fixed pointin the space C([−h,T];X).We firstshow thatΦmaps Brinto itself.Obviously, Φy0∈Br.For t∈(0,T],we have

which means‖Φy‖C([−h,T];X)≤r,Φy⊆Br.

Next,we show thatΦis a contraction mapping on Br.In fact,for any y(·),z(·)∈Br,

Now,we prove the approximate controllability of the system(1)when B=I,where I is the identity operator on X.In this case,U≡X.The semilinear system(1)can be rewritten as

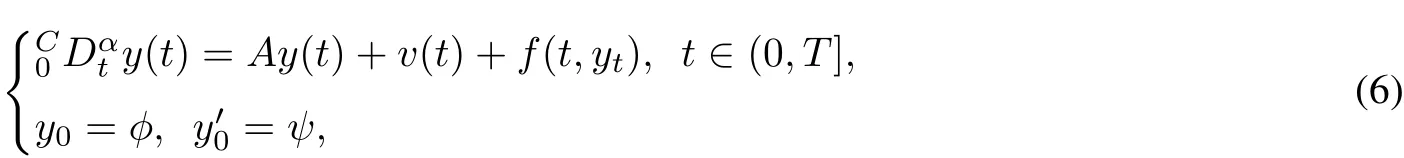
and the corresponding linear system is

Theorem 2 Suppose that(H1),(H2)and(H4)with B≡I hold.Then the semilinearsystem(6)is approximately controllable on[0,T].

Proof From the argument above,we know that if the hypothesis(H4)with B≡I is satisfied,then the corresponding linearsystem(7)is approximately controllable on[0,T],i.e.,X.

Consider the following semilinear system:

By comparing(6)and(8),setting v(t)≡u(t)−f(t,xt)for t∈[0,T],we getthatthe approximate controllability of the system(6)on[0,T]is equivalentto thatofthe system(8).Thus we only need to show thatthe system(8)is approximately controllable on[0,T].

For this purpose,here we shallshow that⊃

By(5),we obtain thatthe mild solution of(8)is

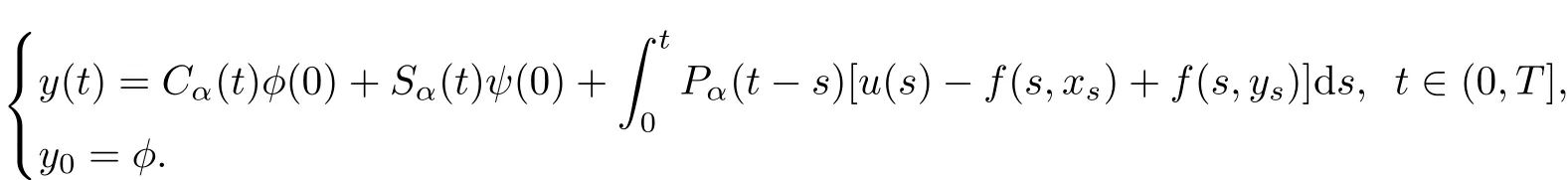
Let x(·)∈C([0,T];X)be the mild solution of the system(7)excited by some control inputs u.Take x(·)∈C([−h,T];X)to be

Then we obtain that

By(H1)and (H2),we have

Then itfollows from(9)and(10)that

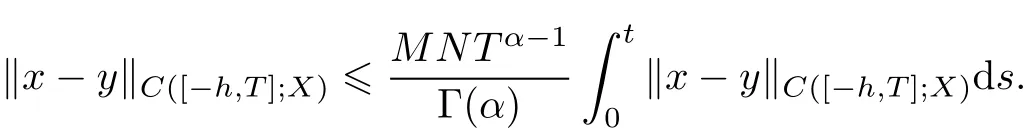
Hence Gronwall’s inequality leads to x(t)=y(t)for all t∈[−h,T].Thatis(f)⊃(0),which means that the system(6)is approximately controllable on[0,T]and the proofis completed.

Finally,we study the approximate controllability ofthe system(1)when B/=I.

Theorem 3 Suppose that(H1)–(H4)hold.Then the semilinearsystem(1)is approximately controllable on [0,T].

Proof Similar to the argumentin Theorem 2,we consider the following semilinear system:

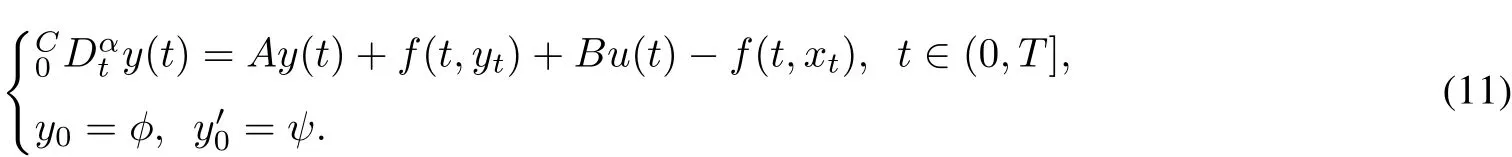
Underthe hypothesis(H3),we can find a controlfunction v to satisfy Bv(t)≡Bu(t)−f(t,xt).Then the approximate controllability of the semilinear system(1)is equivalentto(f)⊃(0).

Note thatthe mild solution of(11)is

Let x(·)∈C([0,T];X)be the mild solution of the system(2)excited by some control inputs u.Take x(·)∈C([−h,T];X)to be

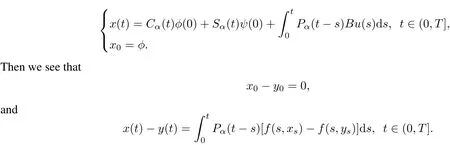
Similarto the proofofthe theorem 2,based on the hypotheses(H1)and(H2),we have

Itthen follows from Gronwall’s inequality that x(t)=y(t)forall t∈[−h,T],and we getthat(f)⊃(0). this implies thatthe system(1)is approximately controllable on[0,T]and the proofis completed.

4 Example

In this section,we give an example to illustrate the effectiveness of ourresult. Consider the following partialdifferentialequation

whereα∈(1,2],φ(θ,z),ψ(θ,z)are continuous functions.

where D(A)={e∈X:e,e′are absolutely continuous,e′′∈X,e(0)=e(π)=0}.Put en(z)=sin(nz); z∈[0,π],n=1,2,···,then{en,n=1,2,···}is an orthogonalset X and enis the eigenfunction corresponding to eigenvalue−n2ofoperator A.Then operator A can be given by

Itis obvious that A is the infinitesimalgeneratorof a strongly continuous cosine family{C(t)}t≥0,defined on X, which is given by

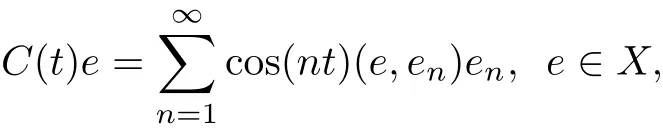
and the associated sine family is given by

Forα∈(1,2),A is the infinitesimal generator of a strongly continuous exponentially bounded fractionalcosine family{Cα(t)}t≥0such that Cα(0)=I(see Theorem 3.1,[17]),and

Then the fractionalsine family{Sα}t≥0and the fractionalRiemann-Liouville family{Pα}t≥0can be given correspondingly.Therefore,the hypothesis(H4)holds.Forevery t∈[0,T],let f(t,y(t+θ,z))=f(t,yt),we can take f(t,yt)=,then the hypothesis(H1)is satisfied.Furthermore,we assume that M=Cα(t)‖+1, B=I and D(B)=R(f),then the hypotheses(H2)and(H3)are satisfied.Hence,the system(12)is approximately controllable.

5 Conclusions

By extending the[10],we discussed the approximate controllability fora class ofsemilinearfractionalevolution equations of orderα∈(1,2]with finite delay.We considered the existence and uniqueness of the mild solution of the system and obtained some sufficientconditions of the approximate controllability of the system.

[1]Oldham K B,Spanier J.The fractionalcalculus:theory and applications ofdifferentiation and integration to arbitrary order [M].New York:Dover Publications Incorporated,2002.

[2]Kilbas A A,Srivastava H M,Trujillo J J.Theory and applications of fractional differential equations[M].Amsterdam: Elsevier Science Limited,2006.

[3]SellR G,You Y C.Dynamics of evolutionary equations[M].Berlin:Springer-Verlag,2002.

[4]El-Borai MM.Some probability densities and fundamentalsolutions of fractionalevolution equations[J].Chaos Solitons and Fractals,2002,14(3):433-440.

[5]Balachandran K,Park J Y.Nonlocal Cauchy problem for abstractfractionalsemilinear evolution equations[J].Nonlinear Analysis,2009,71(10):4471-4475.

[6]Zhou Y,Jiao F.Existence ofmild solutions for fractionalneutralevolution equations[J].Computers and Mathematics with Applications,2010,59(3):1063-1077.

[7]Zhou Y,Jiao F.Nonlocal Cauchy problem for fractionalevolution equations[J].Nonlinear Analysis:Real World Applications,2010,11(5):4465-4475.

[8]JiS C.Approximate controllability ofsemilinearnonlocalfractionaldifferentialsystems via an approximating method[J]. Applied Mathematics and Computation,2014,236(2):43-53.

[9]Shen MY,Kou CH,Guo S J.Approximate controllability offractionalneutralevolution equationswith nonlocalconditions [J].Journalof Shanghai NormalUniversity(NaturalSciences),2016,45(3):253-264.

[10]Sukavanam N,Kumar S.Approximate controllability offractionalordersemilineardelay systems[J].Journalof Optimization Theory and Applications,2011,151(2):373-384.

[11]Kumar S,Sukavanam N.Approximate controllability offractionalordersemilinearsystemswith bounded delay[J].Journal Differential Equations,2012,252(11):6163-6174.

[12]Ge F D,Zhou H C,Kou C H.Approximate controllability of semilinear evolution equations of fractional order with nonlocal and impulsive conditions via an approximating technique[J].Applied Mathematics and Computation,2016, 275(C):107-120.

[13]LiK X,Peng JG,Gao JH.Controllability ofnonlocalfractionaldifferentialsystem oforderin Banach spaces[J].Reports on Mathematical Physics,2013,71(1):33-43.

[14]Qi H Y,Zuo X,Liu J W,etal.Approximate controllability and optimalcontrols of fractionaldynamicalsystems of order 1＜q＜2 in Banach spaces[J].Advances in Difference Equations,2015,73(1):1-17.

[15]Shukla A,Sukavanam N,Pandey D N.Approximate controllability of fractionalsemilinear control system of orderα∈(1,2]in Hilbertspaces[J].Nonlinear Studies,2015,22:131-138.

[16]Shukla A,Sukavanam N,Pandey D N.Approximate controllability of semilinear fractionalcontrolsystems of orderα∈(1,2]with infinite delay[J].Mediterranean Journalof Mathematics,2015,12:1-12.

[17]Bazhlekova E G.Fractionalevolutions equations in Banach spaces[J].Netherland:Eindhoven University of Technology, 2001,14(8):737-745.

[18]Sakthivel R,Ren Y,Mahmudov N I.On the approximate controllability of semilinear fractionaldifferentialsystems[J]. Computers and Mathematics with Applications,2011,62(3):1451-1459.

O 175.15 Document code:A Article ID:1000-5137(2017)03-0384-09

10.3969/J.ISSN.100-5137.2017.03.006

date:2016-07-08

This research was supported by Chinese Universities Science Fund(CUSF-DH-D-2014061).

∗Corresponding author:Kou Chunhai,professor,reseach area:ordinary differentialequations,E-mail:kouchunhai@dhu. edu.cn

family;contraction mapping principle