基于RS和SVM的化工过程高精度故障诊断方法

张 鑫， 胡瑾秋， 张来斌， 王倩琳

(中国石油大学 机械与储运工程学院， 北京 102249)

基于RS和SVM的化工过程高精度故障诊断方法

张 鑫， 胡瑾秋， 张来斌， 王倩琳

(中国石油大学 机械与储运工程学院， 北京 102249)

化工过程长时间处于正常运行状态而积累的故障样本有限，且含有冗余信息，降低了传统故障分类器的准确率。为了提高化工过程故障诊断的准确率，提出了一种基于RS和SVM的化工过程高精度故障诊断方法。首先，在不损失信息的情况下，采用RS约简故障指标体系，去除冗余特征；然后，根据最小约简指标集构建故障数据集，建立优化的SVM故障分类器。将RS-SVM和标准SVM同时应用到预加氢过程的故障分类中，RS不同程度的提高了SVM准确率，当采用RBF核函数且训练样本集容量为60时，准确率提高幅度最大值为11.84%。比较结果表明，剔除数据中的冗余信息有助于提高故障诊断的准确率。

化工过程； 故障诊断； 冗余信息； 粗糙集； 支持向量机

化工过程是一个将危险物质流，高密度能量流和众多信息流汇集于一体的复杂生产系统。其故障问题具有3大特征：(1)由于系统复杂的非线性特性，描述故障模式的信息具有某种程度的不确定性[1]；(2)描述故障状态的特征众多，相关性特征带来大量冗余信息(冗余信息是指一些不必要或不重要的特征，删除它并不影响原始特征的完整性)，干扰故障模式的辨识；(3)化工过程长时间处于正常运行状态，积累的故障样本非常有限。化工过程中一旦发生故障，轻微故障会引起生产系统瘫痪，严重故障会造成有毒物质泄漏，火灾和爆炸等灾难性事故[2]。因此，在保证不损失信息的前提下从故障特征中剔除冗余信息，利用较少故障样本建立高精度的故障诊断方法，对于提高异常工况管理水平，保证化工过程安全平稳运行具有重要意义。

目前，为了减小特征数据中冗余信息对故障诊断效果的影响，国内外通过特征提取和选择方法获取重要的特征。文献[3-6]所采用的方法虽然解除了特征间相关性，突出有用的信息，但只能用于线性问题，不适用于非线性系统。文献[7]是在PCA基础上，引入核函数提取数据的非线性特征，但是其核参数的选取需要人为设定，并且需要大量训练样本才能提取出合理特征。文献[8]将RELIEFF加权特征选择方法和特征相关度算法相结合去除无效特征，该方法突出权值高于特定值的特征，但是权重阈值需要根据经验知识给出，具有一定主观性。上述方法均有利于提高故障诊断模型的精度。近年来，智能诊断方法，如模糊推理[9]、神经网络(BP)[10]、专家系统[11]、支持向量机(SVM)[12]在故障诊断领域得到普遍应用。然而，模糊隶属函数需要根据经验给出；BP只有当数据样本充分的时候才能进行工作；专家系统不利于深层知识的挖掘；SVM在样本较少情况下具有优越的建模能力和泛化性能，但是SVM并不能从高维特征数据中去除冗余信息，影响了故障诊断模型的建模效率和分类性能。而粗糙集(RS)是一种无需任何先验知识，在保证分类精度不变的情况下约简特征，剔除冗余信息的方法，但是其本身泛化能力(推广性能)有限[13]。因此，利用RS和SVM的各自优势，将RS和SVM相结合的方法(简称RS-SVM)，既能约简冗余特征，提高分类器的建模效率和分类性能，又能保证分类模型的泛化性能。RS-SVM已经成功应用到水质评估[14]、贷款违约判别[15]、核设备故障识别[16]等领域。然而，与上述领域的研究对象相比，化工过程的特征变量众多，带有大量冗余信息，且故障样本非常有限，若利用单一的智能诊断方法势必带来建模效率低，诊断精度低的问题。

为了建立适用于化工过程的高精度故障诊断方法，在本研究中提出一种基于RS和SVM的化工过程高精度故障诊断方法。首先应用RS理论对化工过程高维的故障指标进行简化，删除冗余指标；然后采用优化的SVM对RS约简后的故障样本数据进行训练和分类。并以预加氢过程为例进行案例分析，以实现对故障的高精度诊断。

1 故障诊断决策表和支持向量机

1.1 故障诊断决策表

粗糙集在数据预处理和知识约简方面表现出优越的性能，成为了故障诊断领域知识获取的有力工具。知识约简是粗糙集理论应用的核心步骤，所谓知识约简，就是在保持知识分类能力不变的条件下，删除其中的不相关或多余的知识(冗余信息)[17]。故障诊断决策表(Fault diagnostic decision table，FDDT)是粗糙集中对知识进行表达和处理的基本工具，通过对FDDT中故障指标体系及其指标值的化简，可以得到具有更少故障指标的决策表，经过简化的故障指标体系称之为最小故障指标集。FDDT(如表1所示)定义为S=(U，C∪D，V，f)，其中U={x1,x2,…,xn}为诊断对象集，xi(1≤i≤n)为1个诊断实例；C={c1,c2,…,ch}为故障指标体系，tnh为诊断实例xn的ch指标的指标值；D={d1,d2,…,dk}为故障类型集合；且C∩D=Ø，E=C∪D，信息函数f表示U与E的关系集，f={fj|1≤j≤(n+k)}，其中信息函数fj=U→Vj(1≤j≤n+k)，Vj是故障指标ej的值域，ej是指标集合E的1个元素；V是所有指标值域的并集。

表1 故障诊断决策表Table 1 Fault diagnostic decision table

粗糙集理论约简FDDT中故障指标体系的步骤为：

(a) 根据故障指标的阈值区间，将FDDT中连续指标值作离散化处理，得到离散化FDDT。设第h个故障指标的阈值区间和指标值分别为[Lh，Hh]和th，离散值为tH，则离散规则为式(1)：

(1)

(b) 采用删除算法[18]约简离散化的FDDT中冗余指标，得到最小故障指标集。

ROSETTA软件是1个基于粗糙集理论框架的表格逻辑数据分析工具包，提供多种约简属性的算法，由于Johnson’salgorithm偏向于搜索到具有最小长度的单一约简指标集，故在本文中以下内容选用ROSETTA软件的Johnson’salgorithm对FDDT中指标体系进行约简。

1.2 支持向量机

SVM在解决少样本的故障诊断问题时具有较强的泛化性能，而化工过程故障诊断的瓶颈之一是故障样本的缺乏，因此，SVM在化工过程的故障诊断中有很好的应用前景[19]。

SVM是通过核函数，将非线性数据空间映射到线性可分的高维空间进行线性分类或回归，因此，SVM分类器模型可以表示为式(2)。

y=f(φ,γ,g,k(φ,φ*))

(2)

其中φ是输入项(训练数据集)，φ可以看成由故障指标值和故障类型组成的矩阵，如式(3)所示，dk含义见表1，φnh是tnh的离散化值，训练数据集的实例数n≥20。

(3)

γ是惩罚参数，k(φ,φ*)是核函数，主要包括多项式(Polynomial)核函数、径向基(RBF)核函数和多层感知器(Sigmoid)，g是核参数。其中参数γ和g会影响SVM的分类性能，为避免人为设置SVM参数而导致不必要的时间花费和对模型精度的影响，采用基于全局优化的粒子群智能算法[20]寻找最优的γ和g。

2 基于RS和SVM的化工过程高精度故障诊断方法

基于RS理论和SVM方法，适用于化工过程的高精度故障诊断方法的流程图如图1所示，具体的步骤描述如下：

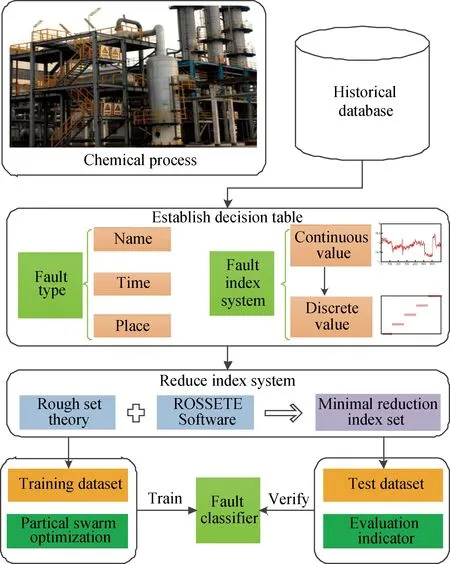
图1 所提出方法的流程图Fig.1 Procedure of the proposed method

步骤1：建立故障诊断决策表

在化工工艺未变更的情况下，调研化工过程的异常工况记录，确定典型的故障类型作为诊断对象；并根据化工过程PI&D图，选取能够描述相应故障的过程变量构建故障指标体系；再从历史数据库(包括异常和正常的工况记录)中选取N(N≥20)个诊断实例，建立如表1所示的故障诊断决策表FDDT。

步骤2：约简故障指标体系

根据1.1节步骤(a)，得到离散化的FDDT；然后采用Johnson’s algorithm约简算法得到最小故障指标集。

步骤3：训练故障分类器

根据步骤2得到的最小故障指标集，建立如公式(3)所示的训练数据集，作为SVM故障分类器的输入项，并采用粒子群算法优化惩罚参数γ和核参数g，最终建立RS-SVM故障分类器。

步骤4：故障诊断

按照步骤2中最小故障指标集和公式(3)，建立样本容量为T的测试数据集，将测试样本集输入到已经建立的RS-SVM故障分类器中，对故障类型进行分类，并将结果列于混淆矩阵(如表2所示)，进一步用于方法性能的评估。根据公式(4)、(5)、(6)可以得到准确率(Accuracy)、漏警率(Missing alarm rate，MAR)和虚警率(False alarm rate，FAR)。

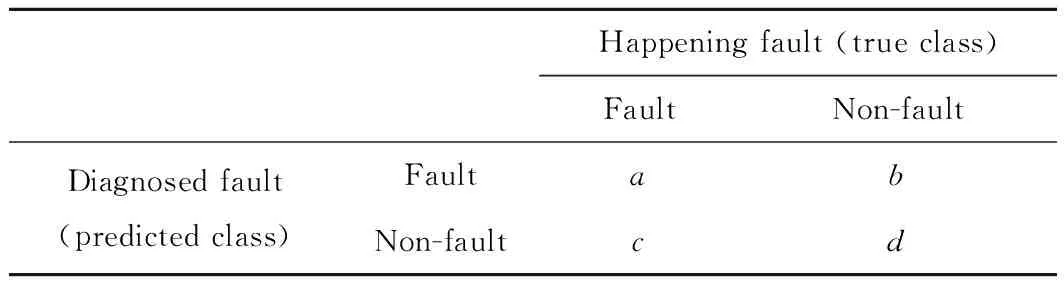
表2 混淆矩阵Table 2 Confusion matrix

Whereais the number of samples assigned to fault mode and correctly diagnosed;bis the number of samples not happened but diagnosed as fault;cis the number of samples happened really but diagnosed as non-fault;dis the number of samples corresponding to non-fault situation and properly diagnosed.

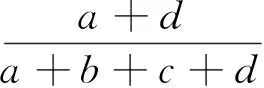
(4)

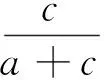
(5)

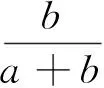
(6)

3 案例研究

预加氢过程是处理重整原料的最重要环节，预加氢作用是除去原料油中的杂质以保护重整催化剂。预加氢的过程是在催化剂和氢气的作用下，使原料中的硫、氮、氧等化合物进行预加氢反应，生成易于除去的H2S、NH3和H2O。典型的预加氢过程如图2所示。预加氢过程积累的故障样本较少，监测数据具有非线性和冗余性的特点，比如，分离罐D-101 调压系统出现故障，现场监测指标包括D-101 入口温度(TI1114)、D-101液位(LIC1109)、D-101压力(PIC1102)和循环氢分液罐D-102压力(PI1112)，其中LIC1109对于描述故障并不重要，因此该变量属于冗余特征。本节针对预加氢过程的异常工况，采用HYSYS软件建立预加氢过程的动态仿真平台，得到不同工况下的仿真数据，验证所提出方法的准确性和有效性。

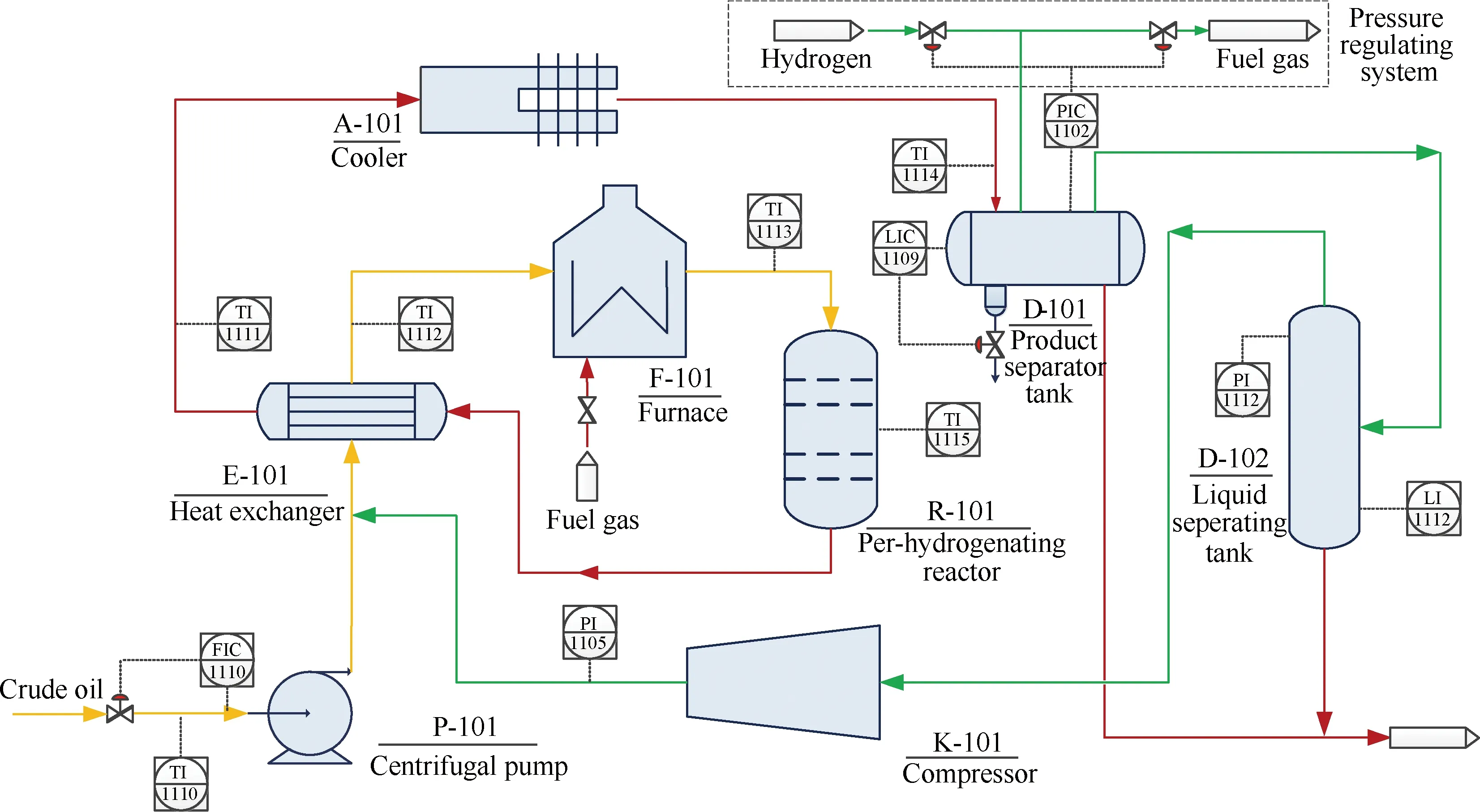
图2 预加氢过程流程图Fig.2 Pre-hydrogenation process flow sheet

步骤1：通过调研预加氢过程的异常工况记录，选取对预加氢过程具有直接影响的4种故障和无故障作为诊断对象，如表3所示，相应的故障指标体系描述如表4所示。通过动态仿真平台模拟表3中故障类型，得到30个实例(包括23个故障实例和7个非故障实例)，建立如表5所示的故障诊断决策表。

步骤2：根据表3中各故障指标阈值区间，得到离散化决策表，如表6所示；约简得到的最小故障指标集包括7个故障指标，分别为：C_1，C_3，C_4，C_5，C_9，C_11，C_12。

步骤3：为了评估所提出方法的性能，通过仿真平台进一步建立样本容量为45、60、75的训练数据集，同时应用3种核函数(即Polynomial、RBF和Sigmoid核函数)建立RS-SVM故障分类器，每种RS-SVM分类器的关键参数如表7所示。

步骤4：建立包含76个实例的测试数据集(包含故障实例58个，无故障实例18个)，采用步骤3建立的12种RS-SVM分类器对每个实例进行故障分类，每种分类器的分类准确率见表8。

表3 故障类型Table 3 Fault type

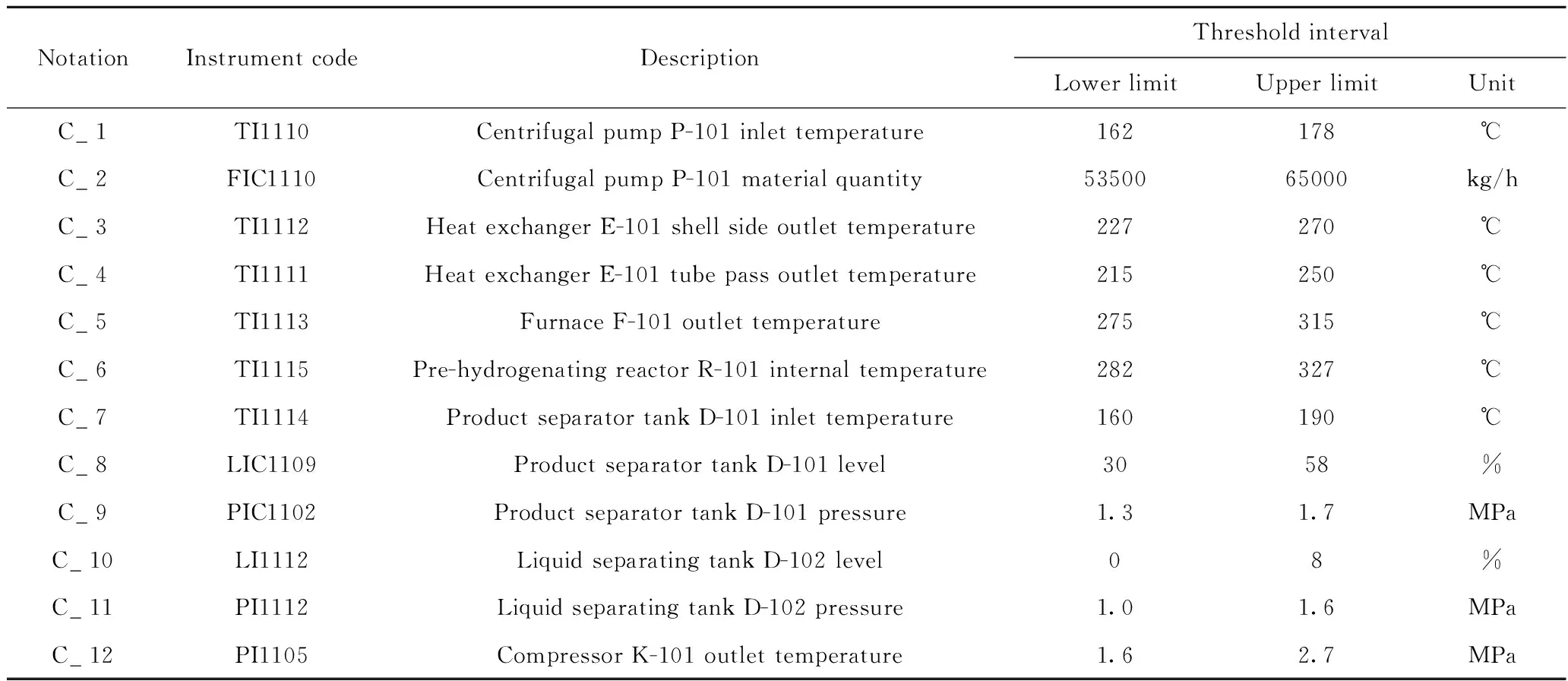
表4 故障指标体系描述Table 4 Description of the fault index system

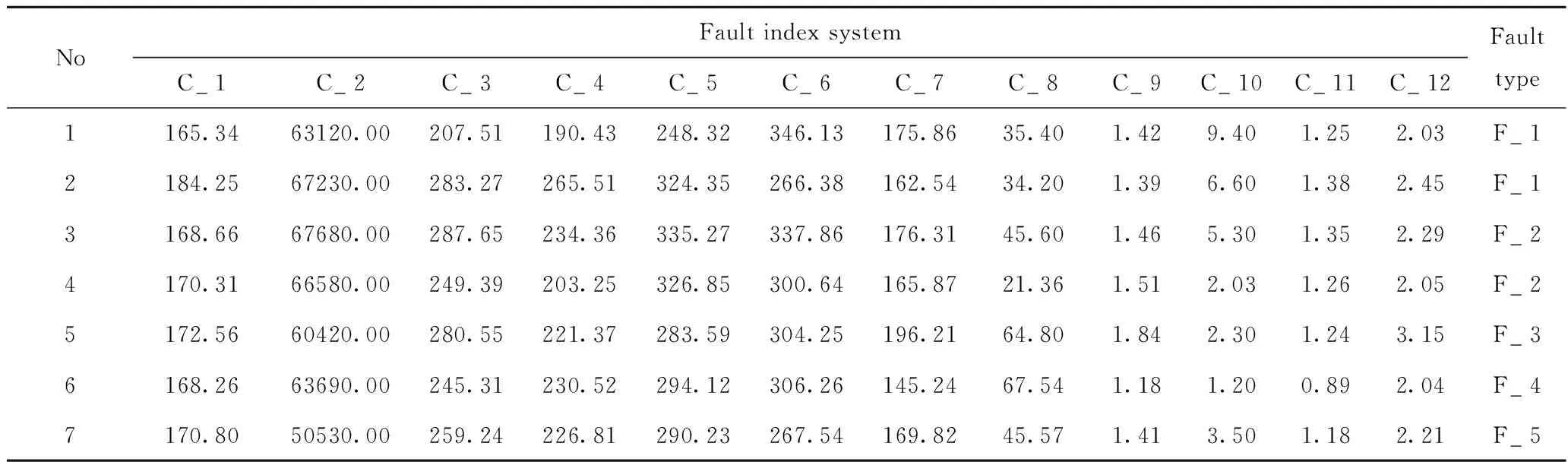
表5 故障诊断决策表(部分)Table 5 Fault diagnostic decision table (part)

4 结果与讨论

为检验RS对SVM分类器准确率的影响，表8对比了使用RS-SVM方法和标准SVM方法所建立的故障分类器对测试样本的判定情况。由表8可以看出，(1) 无论采取哪种训练模式，RS-SVM的准确率均高于标准SVM(其最优参数和g是通过粒子群算法优化得到)的准确率。当采用RBF核函数且训练集样本容量为60时，RS最大幅度的提高了SVM的准确率，提高幅值为11.84百分点。这是因为通过删除冗余指标而减少了噪声源影响，最小故障指标集比原来的故障指标体系更具有代表性，从而有效地提高SVM分类器准确率。(2) 随着训练数据集样本容量增加，整体准确率也逐步增大，说明训练数据集样本容量影响分类器准确率，这种现象可以解释为：训练数据集容量越大，捕捉到的基本问题特征(支持向量)越多，并没有引入误导SVM分类的多余噪声。其中采用RBF的RS-SVM的整体准确率最高，当样本容量为75时，准确率取得最大值，为90.79%。

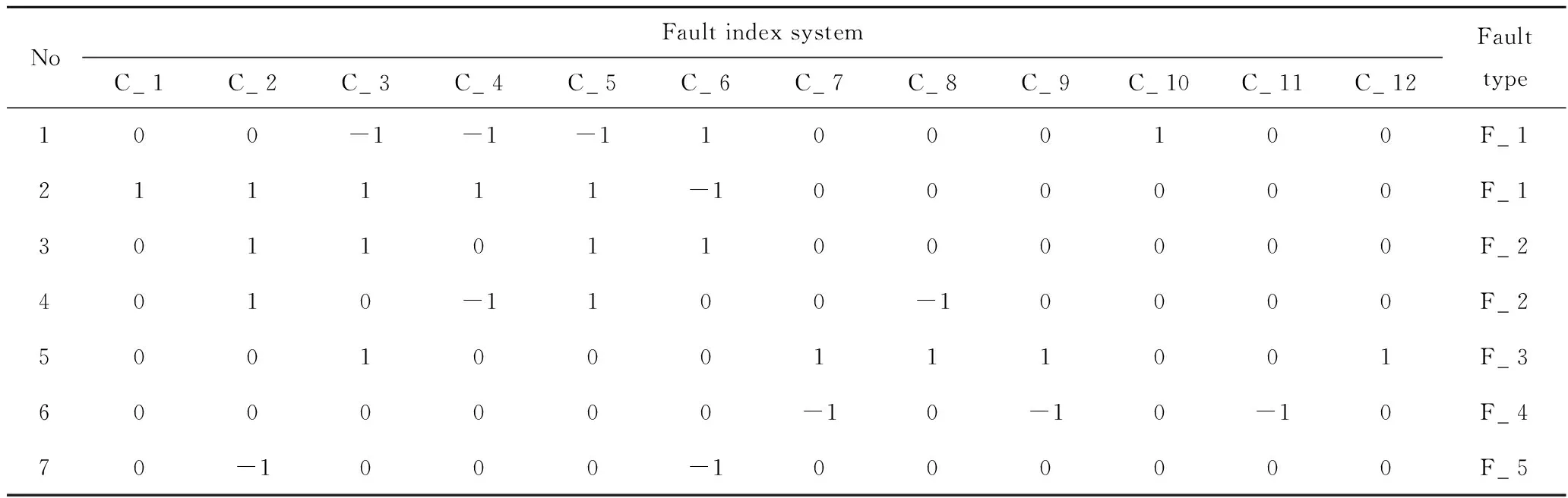
表6 离散化的故障诊断决策表(部分)Table 6 Discrete fault diagnostic decision table (part)

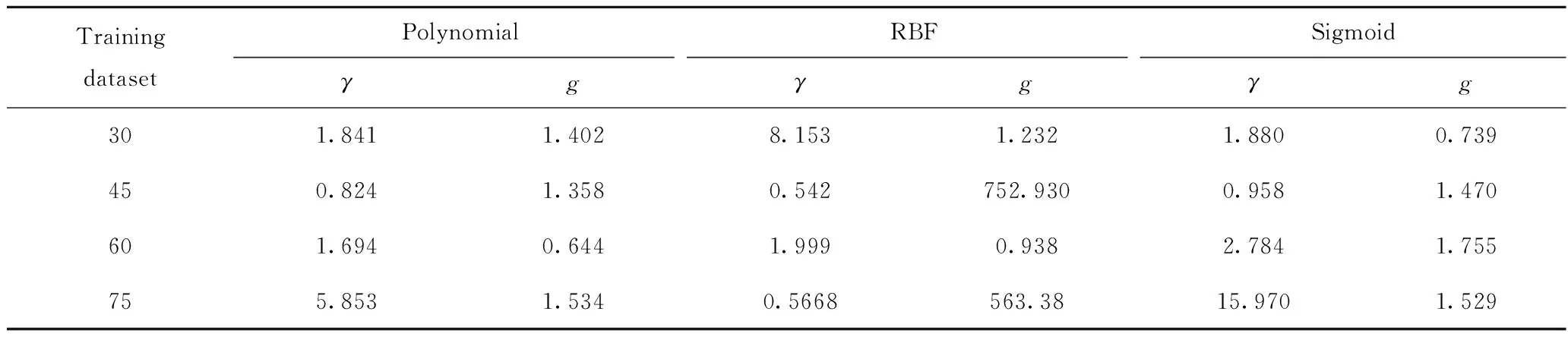
表7 每种RS-SVM分类器的最优惩罚参数γ和最优核函数gTable 7 The optimal penalty factors γ and kernel parameters g of each RS-SVM classifier

表8 RS-SVM和SVM对测试数据集的分类情况Table 8 Classification results of RS-SVM and SVM on test dataset

(3) 在同一种核函数下，RS-SVM方法的准确率随着训练数据集样本容量增加而增大，为了量化这种影响，建立灵敏度指标。灵敏度定义为：同一种核函数类型下，诊断方法因数据集容量变化所致的准确率变化程度，计算式如(7)所示：

Sensitivity=AccuracyMAX-AccuracyMIN

(7)

式中，AccuracyMAX和AccuracyMIN分别表示在同一种核函数下，当训练数据集样本数分别为75和30时，RS-SVM分类器对应的准确率。3种核函数下RS-SVM对训练数据集样本容量的灵敏度如表9所示，Polynomial对训练数据集的样本容量最灵敏，Sigmoid对训练数据集的样本容量最不灵敏，表明采用Polynomial的RS-SVM和Sigmoid的RS-SVM的准确率分别受训练数据集样本数的影响最大和最小。

表9 3种核函数下RS-SVM的灵敏度Table 9 Sensitivity of RS-SVM under three kinds of kernel functions

(4) 当训练数据集样本容量保持不变时，核函数类型对RS-SVM的准确率也有影响，为了量化这种影响，建立鲁棒性指标。鲁棒性定义为：同一种数据类型下，诊断方法因核函数类型不同而导致诊断准确率波动的程度，计算式如(8)所示：

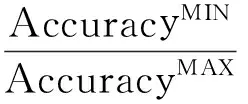
(8)

式中：AccuracyMAX和AccuracyMIN分别表示同一个训练数据集下，使用3种核函数建立的RS-SVM分类器的最大准确率和最小准确率。表10列出了RS-SVM 的鲁棒性指标，在任何一个训练样本集下，鲁棒性指标值均接近1，表明在预加氢过程的故障诊断研究中，RS-SVM对核函数类型具有较强的鲁棒性。

表10 RS-SVM对核函数的鲁棒性Table 10 Robustness of RS-SVM to kernel function

每种故障分类器的漏警率和虚警率如表11所示，随着训练数据集样本数增加，无论采取哪种核函数，故障分类器的漏报警和虚报警的概率均减小。其中采用Polynomial的RS-SVM具有最小的漏警率，表明该分类器能够捕捉更多具有故障特征的支持向量；采用RBF的RS-SVM具有最小的虚警率，表明该方法对非故障的预测效果最优。

5 结 论

(1) 提出了一种基于RS和SVM的化工过程高精度故障诊断方法，解决了故障样本较少且含有冗余信息而影响故障分类器性能的问题。

(2) 所提出方法首先在不损失故障样本信息的前提下，约简故障指标体系，继而在较少的故障数据下，采用粒子群优化的支持向量机建立了高精度的故障诊断器。

(3) 通过将预加氢过程作为应用对象，验证了RS-SVM的有效性和适用性。仿真结果表明，RS-SVM 通过约简故障指标体系，不同程度地提高了故障诊断的准确率，提高幅度最大值为11.84百分点。采用Polynomial的RS-SVM对训练数据集的灵敏度为7.89%，当训练样本容量为75时，采用RBF的RS-SVM虚警率为5.26%。

[1] 马曦， 张来斌， 胡瑾秋， 等. 基于IRML的油气加工系统多层次故障传播模型研究[J].石油学报(石油加工)， 2015， 31(5)： 1193-1202. (MA Xi， ZHANG Laibin， HU Jinqiu， et al. Hierarchical fault propagation model for petroleum refining system based on IRML[J].Acta Petrolei Sinica(Petroleum Processing Section)， 2015， 31(5)： 1193-1202.)

[2] HU J Q, ZHANG L B, MA L, et al. An integrated safety prognosis model for complex system based on dynamic Bayesian network and ant colony algorithm[J].Expert Systems with Applications, 2011, 38(3): 1431-1446.

[3] SHAMS M A B, BUDMAN H M, DUEVER T A. Fault detection, identification and diagnosis using CUSUM based PCA[J].Chemical Engineering Science, 2011, 66(20): 4488-4498.

[4] AJAMI A, DANESHVAR M. Data driven approach for fault detection and diagnosis of turbine in thermal power plant using independent component analysis (ICA)[J].International Journal of Electrical Power & Energy Systems, 2012, 43(1): 728-735.

[5] LI J, LU B L. An adaptive image Euclidean distance[J].Pattern Recognition, 2009, 42(3): 349-357.

[6] TOKKOLA K. Feature extraction by non-parametric mutual information maximization[J].Journal of Machine Learning Research, 2003, 3(7): 1415-1438.

[7] 高绪伟. 核PCA特征提取方法及其应用研究[D].江苏： 南京航空航天大学， 2009.

[8] 王友荣. Relief F加权特征选择方法在旋转机械故障诊断中的应用研究[D].河北： 燕山大学， 2014.

[9] HOU T H, HUANG C C. Application of fuzzy logic and variable precision rough set approach in a remote monitoring manufacturing process for diagnosis rule induction[J].Journal of Intelligent Manufacturing, 2004, 15(3): 395-408.

[10] 赵劲松， 陈丙珍， 沈静珠. 人工神经网络在动态过程故障诊断中的应用[J].石油学报(石油加工)， 1996， 12(1)： 88-97. (ZHAO Jinsong， CHEN Bingzhen， SHEN Jingzhu. Artificial neural networks in dynamic process fault diagnosis[J].Acta Petrolei Sinica(Petroleum Processing Section)， 1996， 12(1)： 88-97.)

[11] 吕翠英， 徐亦方， 沈复， 等. 石油精馏系统故障诊断专家系统中基于深层知识的学习模型——一种不完善理论问题的处理方法[J].石油学报(石油加工)， 1993， 9(4)： 28-34. (LÜ Cuiying， XU Yifang， SHEN Fu， et al. Petroleum distillation system fault diagnosis expert system based on deep knowledge learning model——A kind of imperfect theory approach problem[J].Acta Petrolei Sinica(Petroleum Processing Section)， 1993， 9(4)： 28-34.)

[12] 袁胜发， 褚福磊. 支持向量机及其在机械故障诊断中的应用[J].振动与冲击， 2007， 26(11)： 29-35， 58. (YUAN Shengfa， CHU Fulei. Support vector machine and its application in machine fault diagnosis[J].Journal of Vibration and Shock， 2007， 26(11)： 29-35， 58.)

[13] 张腾飞， 王锡淮， 叶银忠， 等. 粗糙集理论在故障诊断中的应用综述[J].上海海事大学学报， 2005， 26(4)： 20-25. (ZHANG Tengfei， WANG Xihuai， YE Yinzhong， et al. Survey on application of rough set theory in fault diagnosis[J].Journal of Shanghai Maritime University， 2005， 26(4)： 20-25.)

[14] 黄鹤， 梁秀娟， 肖霄， 等. 基于粗糙集的支持向量机地下水质量评价模型[J].中国环境科学， 2016， 36(2)： 619-625. (HUANG He， LIANG Xiujuan， XIAO Xiao， et al. Model of groundwater quality assessment with support vector machine based on rough set[J].China Environmental Science， 2016， 36(2)： 619-625.)

[15] 柯孔林. 基于粗糙集与支持向量机的企业短期贷款违约判别[J].控制理论与应用， 2009， 26(12)： 1365-1370. (KE Konglin. Default prediction of short-term loan based on integration of rough sets and support-vector-machines[J].Control Theory & Applications， 2009， 26(12)： 1365-1370.)

[16] 徐金良， 陈五星， 唐耀阳. 基于粗糙集理论和支持向量机算法的核电厂故障诊断方法[J].核动力工程， 2009， 30(4)： 52-54， 85. (XU Jinliang， CHEN Wuxing， TANG Yaoyang. Study on fault diagnosis in nuclear power plant based on rough sets and support vector machine[J].Nuclear Power Engineering， 2009， 30(4)： 52-54， 85.)

[17] 汪文锋. 基于粗糙集理论的装载机故障诊断研究[D].湖北： 华中科技大学， 2005.

[18] 杨雨时， 张丽娜， 周静. 粗糙集理论在农业机械故障诊断中的应用[J].农机化研究， 2013， 33(4)： 249-252. (YANG Yushi， ZHANG Lina， ZHOU Jing. Application for agricultural mechanical fault diagnosis with rough set theory[J].Journal of Agricultural Mechanization Research， 2013， 33(4)： 249-252.)

[19] 陈念贻， 陆文聪. 支持向量机算法在化学化工中的应用[J].计算机与应用化学， 2002， 19(6)： 673-676. (CHEN Nianyi， LU Wencong. Support vector machine applied to chemistry and chemical technology[J].Computers and Applied Chemistry， 2002， 19(6)： 673-676.)

[20] NIETO P J G, GONZALO E G, LASHERAS F S, et al. Hybrid PSO-SVM-based method for forecasting of the remaining useful life for aircraft engines and evaluation of its reliability[J].Reliability Engineering & System Safety, 2015, 138: 219-231.

High-Accuracy Fault Diagnosis of Chemical Processes Based on RS and SVM

ZHANG Xin， HU Jinqiu， ZHANG Laibin， WANG Qianlin

(CollegeofMechanicalandTransportationEngineering，ChinaUniversityofPetroleum，Beijing102249，China)

Fault diagnosis plays an important role to prevent accidents in chemical processes that are in the normal operation for a long time. However, the limited number of fault samples with redundant information reduces the accuracy of traditional fault classifiers. In order to improve the accuracy of fault diagnosis in chemical processes, a novel fault diagnosis method for chemical processes with redundant information, which integrates the rough set theory (RS) with a support vector machine (SVM), named RS-SVM, is proposed in this paper. In the first stage, RS is utilized to eliminate redundant features by reducing fault index system with no information loss. In the second stage, fault dataset based on minimal reduction index set obtained by RS is employed to establish the optimized SVM classifier. The effectiveness of the proposed method is verified by simultaneously applying RS-SVM and standard SVM to a pre-hydrogenation process. Results reveal that based on the simplicity attribute of RS, the accuracy of SVM is increased in various degrees. When the RBF kernel function is used and the fault sample capacity is 60, the accuracy of SVM is increased by the largest margin, 11.84%. In this aspect, eliminating redundant information is helpful to improve the accuracy of fault diagnosis.

chemical process; fault diagnosis; redundant information; rough set; support vector machine

2016-09-08

国家自然科学基金项目(51574263)、中国石油大学(北京)青年创新团队C计划(C201602)和中国石油大学(北京)科研基金项目(2462015YQ0403)资助

张鑫，男，博士研究生，从事油气生产系统故障诊断及预警研究；E-mail：mofansheng1999@126.com

胡瑾秋，女，教授，博士，主要从事油气生产复杂系统可靠性、故障诊断及预警等研究；Tel：010-89733406；E-mail：hujq@cup.edu.cn

1001-8719(2017)04-0777-08

X937

A

10.3969/j.issn.1001-8719.2017.04.024