多向地震荷载作用下砂土场地震陷分析

高广运，聂春晓，石超，宋健

(1.同济大学 地下建筑与工程系，上海 200092； 2.同济大学 岩土及地下工程教育部重点实验室，上海 200092； 3.国网马鞍山供电公司，安徽 马鞍山 230061； 4.河海大学 土木与交通学院，江苏 南京 210098)

多向地震荷载作用下砂土场地震陷分析

高广运1,2，聂春晓1,2，石超3，宋健4

(1.同济大学 地下建筑与工程系，上海 200092； 2.同济大学 岩土及地下工程教育部重点实验室，上海 200092； 3.国网马鞍山供电公司，安徽 马鞍山 230061； 4.河海大学 土木与交通学院，江苏 南京 210098)

砂土震陷的计算是岩土地震工程的重要问题之一，现有的以经验公式为主的砂土震陷计算方法简化了地震的多维特性。为解决这一问题，本文采用Abaqus有限元软件对地震作用下的砂土场地进行震陷分析，分别模拟砂土场地在单向、水平双向和三向地震荷载作用下的震陷发展规律，并对各方向最大加速度峰值时刻的震陷值和最终震陷进行了对比分析。研究发现震陷的发展经过迅速增长、平稳增加和缓慢发展三个阶段，水平双向地震动引起的震陷值大于水平单向，但小于两个方向荷载单独作用下的和，因此不能简单地采用两个单向荷载作用下震陷叠加等效双向荷载作用下震陷。三向地震荷载引起的震陷远大于水平双向荷载产生的震陷值，竖向地震荷载对场地震陷增大贡献明显。

多向地震荷载；砂土震陷；数值模拟；峰值加速度；竖向地震荷载；震陷等效关系；震陷分析

地震常常会给人类带来巨大的灾难，因此人们对地震预测和地震灾害的评估、治理越来越重视。随着研究的深入，单独以强度准则为地震破坏判断标准已经不能全面反映地震的破坏特点，以变形为控制标准的判断方法越来越受到研究者和工程师的重视。砂土震陷是一种由地震引起的典型变形震害，而地震荷载的不规律性和多维性使得场地震陷计算和评估更为复杂。

Silver等通过室内试验得出净砂的剪应变和体积应变的关系[1]。Tokimatsu等基于剪应变和竖向应变的试验结果建立砂土震陷近似计算方法[2]。Stewart等[3]通过把前人的研究成果嵌入Tokimatsu等[2]计算方法，在深度折减、剪应变等效循环周数、模型衰减、体应变材料模型等方面进行了改进。Ghayoomi等给出非饱和砂土震陷计算建议方法。然而以上这些方法都是计算单一水平方向地震荷载作用引起的震陷量[4]。Pyke等根据试验研究结果，以单向水平地震荷载引起的震陷量的2倍作为水平双向地震荷载引起的震陷量，该震陷等效方式被研究者广泛沿用，成为计算多向震陷的主要方法[5]。然而，理论研究和震害经验表明，多数地震荷载水平分量在振幅和频率特性上有明显差异，水平双向地震荷载作用引起的震陷值是否能够采用两个单向荷载作用下的计算结果还需要进一步验证。另一方面，1995年的阪神地震[6]、1999年的台湾集集地震[7]以及2008年的汶川大地震[8-9]等震害实例表明，当地震震级大且震源深度小时，地震所产生的竖向地震波所引起的场地地震响应不可忽略，甚至有些区域超过了水平向地震波所引起的地震响应。因此Pyke等[5]的震陷转化方法的准确性和全面性有待进一步深入研究。近年来，借助试验方法进行震陷研究取得了较大的进展[10-12]，但因试验仪器的限制，试验或仅可施加多向循环荷载或仅可施加单向地震荷载，无法全面地反映地震的多维性和地震波特性。因此本文基于数值模拟手段，研究多向地震荷载作用引起的砂土场地震陷特性。

1 砂土场地震陷分析模型建立

本文通过建立场地三维模型进行砂土场地震陷分析。土体采用边界面本构模型模拟，该模型使塑性变形以及与之相联系的材料硬化在一个边界面内逐步完成，即有塑性变形逐级积累的特点，适合动荷载下土体变形分析。因Abaqus软件材料库中没有边界面本构模型，所以本文计算采用的模型是在Abaqus的UMAT子程序中进行了二次开发[13]。根据文献[14]对动力边界条件的研究，模拟时在远场设置无限元，采用有限元与无限元相结合的方法处理人工边界，减少地震波在通过人工边界的时候发生反射，以提高计算精确性。本文Abaqus动力分析中的无限元理论参考了Lysmer等[14-16]的工作。

1.1 模型尺寸

计算场地的水平向长宽均为200 m，深度50 m，其中研究核心区域为有限元模拟区域，长宽各为100 m，四周为无限元区域，即在模型4边向内的长度均为50 m。模型共计2 440个单元，其中有限单元1 600个，无限单元840个，结点共计5 819个。在进行震陷研究时，选取场地中心点为震陷特性观测点。模型及网格划分如图1。

图1 场地模型网格图Fig.1 The model grid of ground

1.2 土体参数

本文进行砂土场地的震陷研究，分析中该砂土场地为仅受自重作用的自由场，无上覆荷载作用。选取模拟砂样为美国Silica2#净砂，砂土计算参数选自陈青生等的模拟和Stewart等的试验结果[17-18]，如表1。

表1 不同相对密实度Silica# 2净砂边界面模型参数

Table 1 Parameters of bounding surface model for Silica # 2 sand with different relative densities

相对密度/%加载压缩性常数λ卸载压缩性常数κ临界状态斜率M泊松比μ模型参数H0450016400032812032060001470002941203208000126000253120320

1.3 模型验证

本文计算是在Abaqus软件的二次开发的基础上进行，因此需对数值模拟的准确性和本构模型选取的合理性进行验证。选用相对密度45%、60%和80%的Silica#2砂土进行单元试验模拟，对比在不同剪应变情况下本文模拟值和文献[18]试验值、文献[17]模拟值，因篇幅限制，本文仅列出相对密度45%对比结果，见图2。模拟时采用正弦荷载，循环周数为15周。由图可知，本文模拟结果与Stewart等[18]试验值及陈青生等[17]数值模拟结果接近，趋势相同，说明本文选用的模拟方法有效，可以进行砂土场地震陷分析。

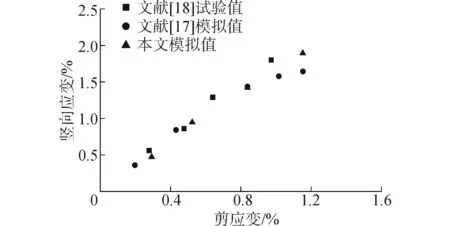
图2 不同剪应变下竖向应变关系Fig.2 Relationship between shear strain and vertical strain

1.4 地震波的选择和输入

本文研究砂土震陷，要求所选取的地震荷载有代表性，且能引起一定的震陷量。选用1940年发生在美国Imperial Valley的El-Centro地震，震级为7.1级，该地震使附近地区80%的建筑物受到不同程度的震害，商业区所有的结构物都受到破坏，大约一半需要关闭维修，所以选用的El-Centro地震可以引发震陷。

El-Centro地震波属于强震地震波，地震发生地Imperial Valley为沙漠地区，且根据地震发生时剪切波速判定为二类场地，与本文分析的砂土自由场地震陷的土层条件类似，据文献[19]关于场地地震波选取的原则，选用该地震波进行多向地震荷载下砂土场地震陷分析。在模拟过程中，地震荷载在模型底部以加速度的形式输入。值得指出的是，本文研究目的在于分析多向地震荷载作用下的震陷发展趋势及震陷量与传统单向地震荷载的区别，以及多维地震中各分向荷载对场地震陷的贡献率，因此本文仅选取了一条具有代表性地震波进行分析，得到地震荷载的多维性对砂土震陷影响的定性结果，明确考虑竖向地震动影响的重要性，并非确定多向地震与单向地震引起震陷比值的定量结果，后者需要通过选取不同种类地震波、不同类型的场地进行综合分析，这将是下阶段的研究内容。

2 不同荷载组合工况下的震陷研究

2.1 地震荷载工况选取

为了分析多向地震荷载对砂土场地震陷的影响，本文主要研究同一场地在不同荷载工况下的震陷特性。在荷载工况的组合上主要选择了El-Centro波的单向时程(两个水平向和竖向)进行输入，探讨在单向地震荷载工况下的场地震陷规律。同时增加了水平双向地震同时输入以及三向地震同时输入的情况，以研究多维地震荷载工况下场地的震陷。具体荷载工况见表2。

表2 地震荷载工况组合情况

2.2 单向地震作用下的场地震陷分析

单向地震作用是指地震荷载单独施加在X向、Y向和Z向时的作用，该分析过程选用的砂土相对密度为45%。

2.2.1 水平单向地震荷载作用下震陷分析

首先研究在单向地震荷载作用下的场地震陷特性。在模拟分析中分别从模型底部输入El-CentroX向地震加速度时程、El-CentroY向地震加速度时程，即地震荷载工况1、2，以研究场地在水平地震波下的震陷规律。模拟结果如图3、4所示。

图3(a)为El-CentroX向地震荷载加速度时程曲线，图3(b)是El-CentroX向地震荷载作用下的竖向应变时程曲线。可以看出，地震引起场地塑性变形，且随着地震的持续，变形逐渐累积，在地震结束时变形累积达到最大值。竖向应变曲线可以分为3个阶段，初始阶段点1、点2之间竖向应变率大，变形增加迅速，在该段内加速度峰值较大，但该段时间较短。点2、点3为竖向应变的第二阶段，此阶段内的加速度峰值也较大，且该段持续时间较长，所以该段时间内的竖向累积量也较大。最后一个阶段为点3之后，随着荷载的逐渐减小，竖向应变缓慢发展，直到震动结束。

图4(a)为El-CentroY向地震荷载加速度时程曲线，图4(b)是El-CentroY向地震荷载作用下竖向应变时程曲线，与X向荷载下的竖向应变规律类似，变形分为3个阶段，初始竖向应变迅速增长阶段，点1到点2之间，该阶段变形快速增加，但持续时间较短；点2到点4之间为竖向应变平稳增加阶段，点4之后加速度峰值变小，对应的竖向应变缓慢发展，直到震动结束。

El-CentroY向地震荷载的最大加速度峰值为点3，处于变形发展的第二阶段内。但因砂土在震动初始发生时段比较松散，所以竖向应变增大最为明显的是震陷的第一阶段。

2.2.2 竖向地震荷载作用下震陷时程

为了研究在竖向地震荷载作用下的场地震陷情况，采用El-CentroZ向地震加速度时程，如图5(a)，从场地三维模型底部输入，即荷载工况3，震陷变化如图5(b)。由图可知，Z向荷载下竖向应变随时间增长过程也可以分为3个阶段：变形迅速增长阶段、变形平稳增加阶段、变形缓慢发展阶段。

图3 El-Centro X向地震荷载与竖向应变时程图Fig.3 Earthquake loading in X direction and vertical strain time history

图4 El-Centro Y向地震荷载与竖向应变时程图Fig.4 Earthquake loading in Y direction and vertical strain time history

图5 El-Centro Z向地震荷载与竖向应变时程图Fig.5 Earthquake loading in Z direction and vertical strain time history

Z向荷载作用下，震陷累积过程总体趋势增大，但在加载的某些时刻，土体的竖向应变出现锯齿状的上下波动，与X、Y向荷载下的震陷曲线不同。可能因为El-CentroZ向地震荷载为压缩波，为竖向震动，而竖向为震陷发生的方向，Z向的上下波动会直接引发砂土在竖向某一时刻的压密与松散，故形成锯齿状的竖向应变曲线。

对比Z向荷载下竖向应变与X向、Y向荷载下差异，震动在3个方向的持时相同，最大加速度峰值接近，但它们引发的震陷量差异却很大，竖向震陷量比水平向大2倍多。产生如此差异的原因可能是竖向震动的地震波为压缩波而水平震动为剪切波，竖向震动对砂土密实的作用更为直接。因此相同情况下，竖向地震动震陷量比水平震陷量大很多，表明在真实情况下竖向震动发挥的作用也大于水平作用，而目前沿用的Pyke等[5]震陷经验等效方法中没有考虑竖向地震的影响，所以现在的震陷等效方法存在一定的缺陷，震陷等效方法的准确和全面性有待进一步研究。

2.3 多向地震作用下的场地震陷

对于多向地震荷载作用下的震陷研究，主要考虑水平双向地震共同作用下的震陷和水平双向加竖向组成的三向地震荷载下的震陷，此分析过程选用的砂土相对密度为45%。

多向震陷分析时荷载的选取和输入也是问题的关键之一，本文采用Abaqus软件进行模拟，在软件中可以设置地震输入的维数，也可确保双向水平地震荷载或三向地震荷载同步输入。本文地震荷载是从模型底部输入。提取模拟后模型底部荷载与输入荷载的大小、形状进行对比，二者改变很小。因模型底部为基岩，对地震荷载的减弱和增大作用很弱，对比结果说明多向地震荷载输入可靠、合理。

2.3.1 水平双向地震荷载作用下震陷

模拟时在模型底部同时输入El-CentroX向和El-CentroY向地震加速度时程，即荷载工况4，模拟结果如图6所示。

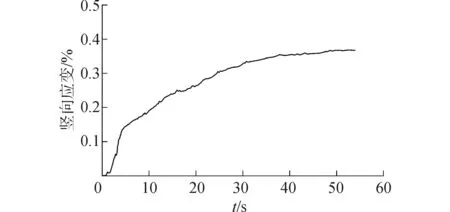
图6 El-Centro 水平双向地震荷载作用竖向应变时程图Fig.6 Vertical strain time-history under bidirectional horizontal directions earthquake loadings

水平双向地震作用下的竖向应变时程曲线基本上呈现和水平单向时程相类似的规律。但它们产生的震陷量却有差别，双向荷载下的震陷量大于单向的结果，小于2个单向震陷量的叠加。研究中没有发现水平单向震陷量的叠加等于水平双向震陷量的规律。

2.3.2 三向地震荷载作用下震陷

在模型底部同时输入El-CentroX、Y、Z向地震荷载的竖向应变发展规律(荷载工况5)，如图7所示，模拟场地在真实地震波作用下震陷规律。三向地震荷载作用下的竖向应变时程曲线在发展趋势上与竖向地震荷载作用下的竖向应变时程曲线更为接近，也明显分成3段。相比竖向荷载单独作用的结果，三向荷载同时作用引起的竖向应变累积曲线整体光滑，没有上下波动，竖向应变平稳增加。

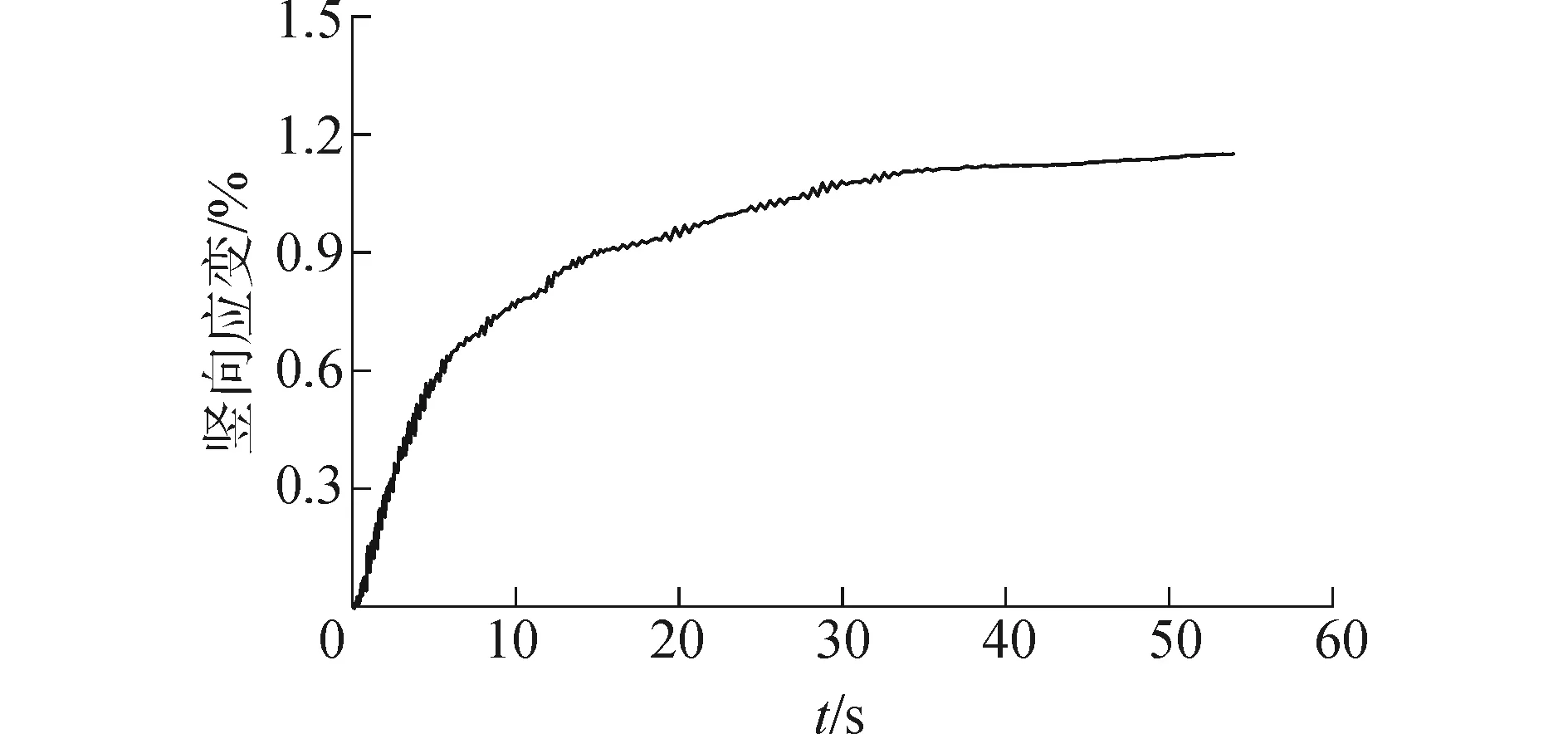
图7 El-Centro 三向地震荷载与竖向应变时程图Fig.7 Earthquake loadings in three directions and vertical strain time-history

2.4 不同工况震陷终值对比分析

为了清楚分析不同工况震陷特性，以及地震荷载维数对震陷的影响，把不同地震荷载工况下最终震陷量用柱状图表示，如图8所示。由图可知，X向(工况1)、Y向(工况2)震动的竖向应变接近，而竖向震动(工况3)比XY水平单向震陷值大很多，分别为它们的2.70倍和2.06倍，水平双向荷载(工况4)的竖向应变大于X向、Y向的竖向应变，分别为它们的1.48倍和1.23倍，小于Pyke等提出的2倍震陷等效转化关系。工况3的竖向应变为0.669%，比单独水平震动和水平双向产生的竖向变形都大。如果三向荷载同时施加(工况5)，即模拟真实地震荷载产生的竖向应变，其值为1.15%，是水平双向震陷的3.13倍，远大于水平双向荷载震陷，也大于单独竖向荷载震陷，说明竖向震动和水平震动耦合后发生的震陷更大，震陷分析中应全面考虑三向荷载作用，合理选用震陷等效转化关系。

图8 不同荷载工况下的最终竖向应变值Fig.8 The final vertical strain in different conditions

2.5 不同向荷载最大加速度峰值时刻震陷对比分析

最大加速度峰值是地震动的重要参数，虽然它为某一时刻的加速度值，但因其幅值巨大，往往会在地震中产生极大的破坏作用，为了研究加速度峰值时刻震陷量在最终震陷中的比值以及分析其是否在砂土震陷中起到决定性的作用，在本节中选取各工况分别在3个方向荷载最大峰值加速度时刻的竖向应变值，然后进行归一化处理，即最大峰值加速度时刻所发生的竖向应变占该工况最终竖向应变的比值，以探究各地震波最大加速度峰值对震陷的贡献情况。El-Centro地震波的持续时间为54 s，各单向峰值加速度处的时刻见表3。

表3 各地震单向荷载加速度峰值出现的时刻

Table 3 The peak ground acceleration time of earthquake in different directions

地震荷载最大峰值加速度时刻/sX214Y1146Z1

图9中表示5种工况分别在t=1 s、t=2.14 s和t=11.46 s时归一化后的竖向应变比。

t=1 s是竖向荷载最大加速度峰值时刻，工况3(竖向荷载)和工况5(三向荷载)产生的竖向应变比占总应变的13.87%和10%，在震动刚开始就产生如此大的震陷是因为竖向荷载促使震陷量增大，且El-Centro竖向地震波在开始阶段幅值较大。

图9 各工况在不同加速度峰值时刻的归一化竖向应变比Fig.9 The ratio of normalized vertical strain at different peak ground acceleration time

t=2.14 s时刻是X向地震波最大加速度峰值时刻，但工况1(单独X向震动)和工况4(水平双向震动)产生竖向应变比值较小，分别为5.81%和10.19%，该比例表明单独的最大峰值加速度并不能明显增大震陷值。

t=11.46 s为Y向地震波最大加速度峰值时刻，此时5种工况的竖向应变比都在50%以上，所有应变比均较大的原因是在t=11.46 s之前3个方向的加速度峰值都比较大且相对集中，在此后加速度峰值逐渐减小，即在此之前地震波集中了大部分能量，因此大部分竖向应变在该时段内发生。因此，最大峰值加速度可增加该时刻的竖向应变速率，并不能明显加大最终的竖向应变。

2.6 相对密度对不同维度震陷比值影响

据文献[1-4]可知，砂土相对密度对震陷影响巨大，相对密度增大，震陷量减小。图10是相对密度分别为45%、60%和80% Silica#2水平双向荷载作用震陷与水平单向荷载作用震陷比值(水平单向荷载作用方向为X向，在Y向荷载作用的结果与X类似，仅列出X向作用结果)、三向震陷与水平双向震陷比值、三向震陷值与水平单向震陷比值(X方向荷载震陷值)。由图可知，随着相对密度增大，不同维度荷载作用下震陷比值稍有增大，但比值变化很小，说明虽然砂土相对密度和地震荷载作用维度对砂土震陷影响很大，但砂土相对密度对不同维度地震荷载产生的震陷比值的影响很小。

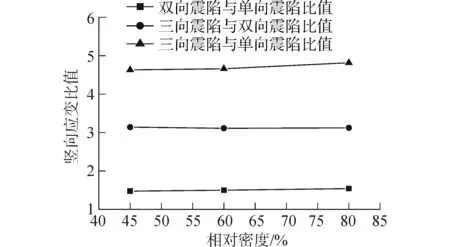
图10 相对密度对不同维度震陷比值的影响Fig.10 Effects of relative densities on seismic compression ratio of different dimension

3 结论

1)震陷的发展大约分为3个阶段：变形迅速增长阶段、平稳增加阶段以及缓慢发展阶段。初始变形快速增长阶段占整个地震动持时有限，但产生的震陷累积却较大。

2)水平双向震陷量不能简单的用2个单向震陷量叠加等效，水平双向震陷大于水平单向震陷，小于两个单向荷载作用之和。

3)竖向荷载对多向震陷的贡献量巨大。当加速度峰值相近时，竖向地震波作用下的竖向应变比水平向作用的竖向应变大。水平地震荷载和竖向荷载共同作用引发的震陷明显大于仅有水平荷载作用，因此砂土震陷分析既要考虑水平荷载又要考虑竖向荷载。

4)砂土相对密度对震陷影响明显，但不同相对密度砂土场地在多向和单向地震荷载作用下震陷的比值基本相同。

5)本研究仅对砂土自由场地进行分析，并未对其他类型场地进行分析，今后对其他类型的场地进行震陷研究。地震荷载选用El-Centro地震波，该地震波属于强震记录，建议对其它类型的地震波进行分析。

[1]SILVER M L, SEED H B. Volume changes in sands during cyclic loading[J]. Journal of soil mechanics and foundations division, 1971, (SM9): 1171-1182.

[2]TOKIMATSU K, SEED H B. Evaluation of settlements in sands due to earthquake shaking[J]. Journal of geotechnical engineering, 1987, 113(8): 861-878.

[3]STEWART J P, WHANG D H. Simplified procedure to estimate ground settlement from seismic compression in compacted soils[C]//Proceedings 2003 Pacific Conference on Earthquake Engineering. Christchurch, New Zealand, 2003.

[4]GHAYOOMI M, MCCARTNEY J S, KO H. Challenges in prediction earthquake-induced settlements of partially saturated sands[J]. Journal of geotechnical and geoenvironmental engineering, 2013, 139(3): 367-376.

[5]PYKE R M, CHAN C K, SEED H B. Settlement of sands under multidirectional shaking[J]. Journal of the geotechnical engineering division, 1975, 101(4): 379-398.

[6]罗奇峰，那向谦. 1995 年日本阪神地震近场强地面运动的特征[J]. 西北地震学报, 1997, 19(3): 52-55. LUO Qifeng, NA Xiangqian. Characteristics of strong ground motions in epicentral region of the 1995 Osaka Kobe earthquake, Japan[J]. Northwest seismological journal, 1997, 19(3): 52-55.

[7]周正华，周雍年，卢滔,等. 竖向地震动特征研究[J]. 地震工程与工程振动, 2003, 23(3): 25-29. ZHOU Zhenghua, ZHOU Yongnian, LU Tao, et al. Study on characteristics of vertical ground motion[J]. Earthquake engineering and engineering vibration, 2003, 23(3): 25-29.

[8]张勇，冯万鹏，许力生,等. 2008 年汶川大地震的时空破裂过程[J]. 中国科学地球科学:中文版, 2008, 38(10): 1186-1194. ZHANG Yong, FENG Wanpeng, XU Li, et al.Spatial and temporal rupture process of 2008 Wenchuan earthquake[J]. Science in China: earth science, 2008, 38(10): 1186-1194.

[9]孙柏涛，袁一凡. 汶川Ms 8.0级地震工程震害概览[M]. 北京: 科学出版社，2008:10-25. SUN Botao, YUAN Yifan. Ceneral introduction of engineering damage of WenchuanMS8.0 earthquake[M]. Beijing: Science Press, 2008.

[10]陈青生，熊浩，高广运. 基于R-N非线性疲劳损伤累积模型的砂土震陷计算方法[J]. 岩土工程学报, 2013, 35(12): 2203-2211. CHEN Qingshen, XIONG Hao, GAO Guangyun. Procedure for evaluating seismic compression in sands based onR-N cumulative damage fatigue nolinear model[J]. Chinese journal of geotechnical engineering, 2013, 35(12): 2203-2211.

[11]陈青生，熊浩，高广运.地震荷载特征及其对砂土震陷影响试验研究[J].岩土工程学报, 2014, 36(8): 1483-1489. CHEN Qingshen, XIONG Hao, GAO Guangyun. Experimental stdudy on properties of seismic loading and its influence on seismic compression in sands[J]. Chinese journal of geotechnical engineering, 2014, 36(8): 1483-1489.

[12]CHANG W. Evaluation of undrained shear strains in multi-directional horizontal shaking[J]. Soil dynamics and earthquake engineering, 2011, 31(7): 906-920.

[13]费康, 刘汉龙. 边界面模型在ABAQUS的开发应用[J]. 解放军理工大学学报:自然科学版, 2009, 10(5): 447-451. FEI KANG, LIU HANLONG. Implementation and application of bounding surface model in ABAQUS[J]. Journal of PLA University of Science and Technology: natural science edtion, 2009, 10(5): 447-451.

[14]戚玉亮，大塚久哲. ABAQUS 动力无限元人工边界研究[J]. 岩土力学, 2014, 35(10): 3007-3012. QI Yuliang, HISANORI O. Studay of ABAQUS dynamic infinite element artificial boundary[J]. Rock soil mechanics, 2014, 35(10): 3007-3012.

[15]LYSMER J, KUHLEMEYER R L. Finite dynamic model for infinite media[J]. Journal of the engineering mechanics division, 1969, 95(4): 859-878.

[16]KUHLEMEYER R L, LYSMER J. Finite Element method accuracy for wave propagation problems[J]. Journal of soil mechanics and foundations division, 1973, 99(5): 421-427.

[17]陈青生，高广运，何俊锋. 地震荷载不规则性对砂土震陷的影响[J]. 岩土力学, 2011, 32(12): 3713-3720. CHEN Qingshen, GAO Guangyun, HE Junfeng. Effect of irregularity of earthquake loading on seismic compression of sand[J]. Rock and soil mechanics, 2011, 32(12): 3713-3720.

[18]STEWART J P, WHANG D H, MOYNEUR M, et al. Seismic compression of as-compacted fill soils with variable levels of fines content and fines plasticity[C]// Consortium of Universities for Research in Earthquake Engineering. Richmond, CA, 2004:30-35.

[19]KRAMER S L. Geotechnical earthquake engineering[M]. USA: Rrentice Hall, 1996:323-330.

本文引用格式：

高广运，聂春晓，石超，等. 多向地震荷载作用下砂土场地震陷分析[J]. 哈尔滨工程大学学报， 2017， 38(7): 1100-1106.

GAO Guangyun, NIE Chunxiao, SHI Chao, et al. Seismic subsidence of sand ground subject to multidirectional earthquake load[J]. Journal of Harbin Engineering University， 2017， 38(7): 1100-1106.

Seismic subsidence of sand ground subject to multidirectional earthquake load

GAO Guangyun1,2, NIE Chunxiao1,2, SHI Chao3, SONG Jian4

(1.Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China; 2.Key Laboratory of Geotechnical And Underground Engineering of The Ministry of Education, Tongji University, Shanghai 200092, China; 3.State Grid Ma’Anshan Power Supply Company, Ma’anshan 230061, China; 4.College of Civil And Transport Engineering, Hohai University, Nanjing 210098, China)

Calculation of the seismic subsidence of sand is an important issue in geotechnical earthquake engineering. Present empirical methodologies for estimating the seismic subsidence of sand simplify the multidimensionality of earthquakes. Therefore, seismic subsidence of sand under earthquake shock was analyzed via Abaqus finite-element software. The development processes of seismic subsidence were simulated under unidirectional, bidirectional, and multidirectional earthquake loads. The seismic subsidence at the largest acceleration and in every direction and the final subsidence were compared and analyzed. The study found that the development of seismic subsidence comprised three stages: rapid growth, steady increase, and slow development. During these stages, the seismic subsidence under bidirectional excitation was larger than that under unidirectional earthquake load but smaller than the sum of two unidirectional results. Therefore, we cannot simply add the seismic subsidence generated under two unidirectional loads and make the result equivalent to the subsidence under the bidirectional load. The seismic subsidence generated under three-directional earthquake load was much larger than that induced by bidirectional horizontal seismic load. The vertical seismic load plays a huge role in seismic subsidence.

multidirectional earthquake loading; seismic subsidence of sand; numerical simulation; peak acceleration; vertical seismic loading; seismic equivalent relationship of seismic subsidence; seismic compression analysis

2016-08-26.

日期：2017-04-27.

国家自然科学基金项目(41372271).

高广运(1961-)，男，教授，博士生导师； 聂春晓(1988-)，男，博士研究生.

聂春晓，E-mail: niechunxiao123@163.com.

10.11990/jheu.201608054

TU47

A

1006-7043(2017)07-1100-07

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20170427.1630.172.html