轴向拉压型金属阻尼器抗震性能测试及其应用研究
2017-08-31代桂霞
鲁 亮, 刘 霞, 代桂霞
(1.同济大学 结构工程与防灾研究所,上海 200092;2.东南大学 城市工程科学技术研究院,南京 210096)
轴向拉压型金属阻尼器抗震性能测试及其应用研究
鲁 亮1, 刘 霞2, 代桂霞1
(1.同济大学 结构工程与防灾研究所,上海 200092;2.东南大学 城市工程科学技术研究院,南京 210096)
以一种轴向拉压型金属阻尼器为研究对象,介绍了轴向拉压型金属阻尼器的结构构造及其理论计算方法;进行了抗震性能测试,得到了轴向拉压型金属阻尼器的屈服位移、屈服荷载及屈服刚度,并分析了其耗能能力;研究了轴向拉压型金属阻尼器在体外预应力自复位结构中的应用。研究结果表明:轴向拉压型金属阻尼器利用腹板轴向拉压耗能,避免了连接构件的局部损坏;安装方式与黏滞阻尼器相同,安装方便、易于更换;轴向拉压型金属阻尼器具有提供结构附加刚度,控制结构位移,耗能显著的优点。
轴向拉压型金属阻尼器;抗震性能;拟静力试验;耗能能力
基于经济与损失均衡的考虑,根据现行的建筑结构抗震设防目标,建筑结构在强烈地震作用下产生一定程度的损伤是不可避免的,因此在结构抗震设计中有效控制结构的损伤部位和损伤程度是非常重要的理念。近几十年来发展了结构主动控制、被动控制和混合控制的抗震方法[1-3],比较成熟的被动控制抗震方法中又有隔震、耗能减震等技术方法,工程应用中主要利用耗能装置进行结构的隔震和耗能减震。耗能装置可分为:速度相关型(如黏滞阻尼器、黏弹性阻尼器等);位移相关型(如金属屈服阻尼器、摩擦阻尼器等)[4]。
金属阻尼器是一种耗能性能优越、构造简单、制作方便、造价低廉、易于更换的耗能减震装置。在地震作用下,金属阻尼器在结构构件发生塑性变形前先发生屈服,消耗了大部分地面运动传递给建筑结构的能量。它既可以配合隔震支座和隔震系统,作为其中的耗能单元或限位装置,又可以单独用于建筑结构中作为耗能装置,提供附加阻尼和刚度,目前使用的金属阻尼器大多属于剪切加载型阻尼器[5],其上下端面钢板通过锚固螺栓或焊接连接到框架梁底及下部人字形支撑顶部,在剪力作用下使金属腹板剪切耗能。但是框架结构层间侧移引起的竖向位移量与阻尼器的竖向变形量一般不相同,阻尼器上端面钢板挤压梁底,导致主体结构局部损坏。
为克服常规金属阻尼器的缺点,减少地震作用时可能产生的对主体结构构件的破坏,本文提出了一种轴向拉压型金属阻尼器,介绍了轴向拉压型金属阻尼器力学参数的计算方法,进行了轴向拉压型金属阻尼器的抗震性能测试,研究了轴向拉压型金属阻尼器在建筑结构中的耗能特性。
1 轴向拉压型金属阻尼器
1.1 结构构造
轴向拉压型金属阻尼器[6]的构造图如图1所示,该阻尼器包括中心钢板、设置在中心钢板两侧的翼缘板以及设置在中心钢板与翼缘钢板之间的多个耗能腹板,中心钢板与构件固定连接,耗能腹板将中心钢板与翼缘板连接。中心钢板设有一对,共面对称布置;翼缘钢板设有一对,分别沿中心线对称设置在中心钢板两侧;耗能腹板选用多块X形钢板,平均分为数组,分别对称布置在中心钢板与翼缘板之间。耗能腹板的屈服耗散了地震中输入的能量,同时对建筑结构位移响应进行了有效的控制。
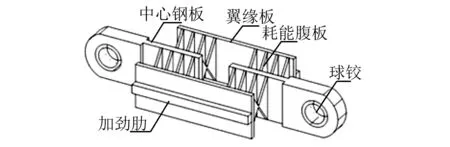
图1 轴向拉压型金属阻尼器结构构造Fig.1 Constructional detail of axial compression-tension metallic damper
轴向拉压型金属阻尼器在建筑结构中的安装如图2所示,框架层间安装人字撑,铰支座通过焊接或螺栓与人字撑连接,梁底预埋铰支座,利用钢插销将轴向拉压型金属阻尼器与梁底以及人字撑铰支座连接。地震作用时,框架产生层间变形,轴向拉压型金属阻尼器承受轴向拉压荷载,耗能腹板变形耗能,消耗了地震能量,控制了层间变形;轴向拉压型金属阻尼器上表面与梁底面留有间隙,在结构往复运动过程中,垂直于框架方向不会对梁底产生挤压。
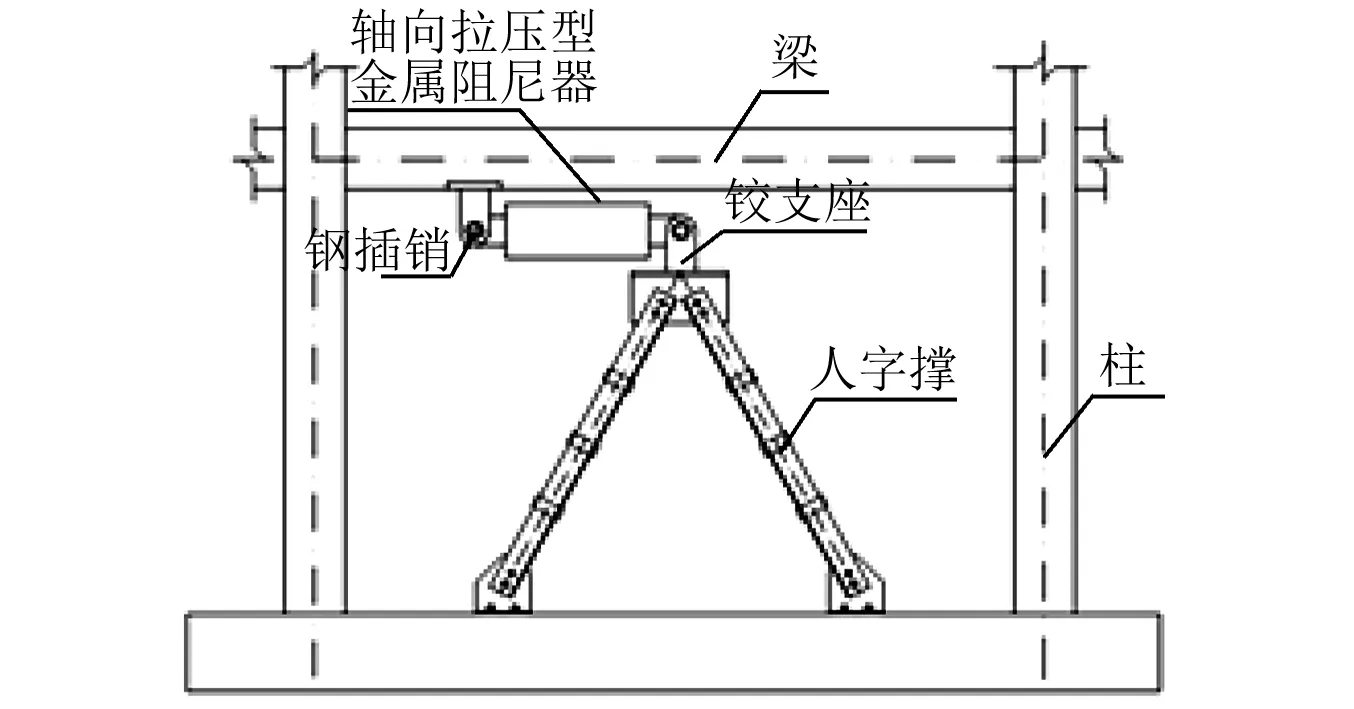
图2 轴向拉压型金属阻尼器安装方式Fig.2 Installation of axial compression-tension metallic damper
与剪切型加载金属阻尼器相比,本文设计的轴向拉压型金属阻尼器优点显著:①安装方式与黏滞阻尼器相同,在结构采用黏滞阻尼器与金属阻尼器进行混合减震控制时,两种阻尼器的安装方式一致,操作方便;②腹板利用轴向拉压进行屈服耗能,避免了剪切加载型金属阻尼器与整体结构变形不协调,挤压梁底,造成结构局部破坏的问题。
1.2 力学参数计算
在设计阻尼器前,需要通过理论计算对其力学参数进行初步计算,得到其大致外形尺寸,再通过有限元软件进行数值分析,最终得到工程设计所需的阻尼器设计参数。
轴向拉压型阻尼器装置的初始刚度、屈服荷载、屈服位移是试验和分析时所必需的参数,下面分别对其进行理论推导。
为了便于分析,在理论推导之前,作如下假定:①不考虑轴力与剪力引起的变形(小一量级),仅考虑阻尼器腹板的弯曲变形;②在弯曲变形过程中,腹板横截面始终保持为平面,即平截面假定。
取阻尼器中一片X形腹板,建立坐标如图3所示,X形钢板的高度为h,宽度为b,厚度为t,X形钢板最窄处宽b0,在高度为y处,X形钢板截面参数如图3所示。
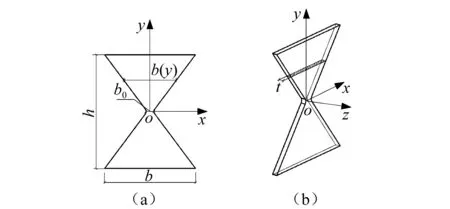
图3 轴向拉压型金属阻尼器X形腹板Fig. 3 X-shaped web of axial compression-tension metallic damper
X形腹板宽度为
(1)

对x轴的惯性矩为
(2)
X形腹板受力简图及内力图如图4和5所示,腹板的主受力方向与厚度方向垂直,且消能钢板的高度远大于其厚度,故腹板变形以弯曲变形为主。
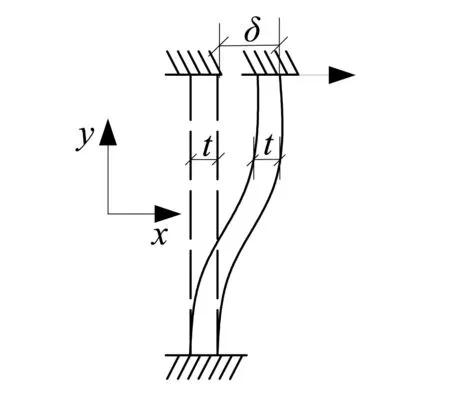
图4 计算简图Fig.4 Computing model
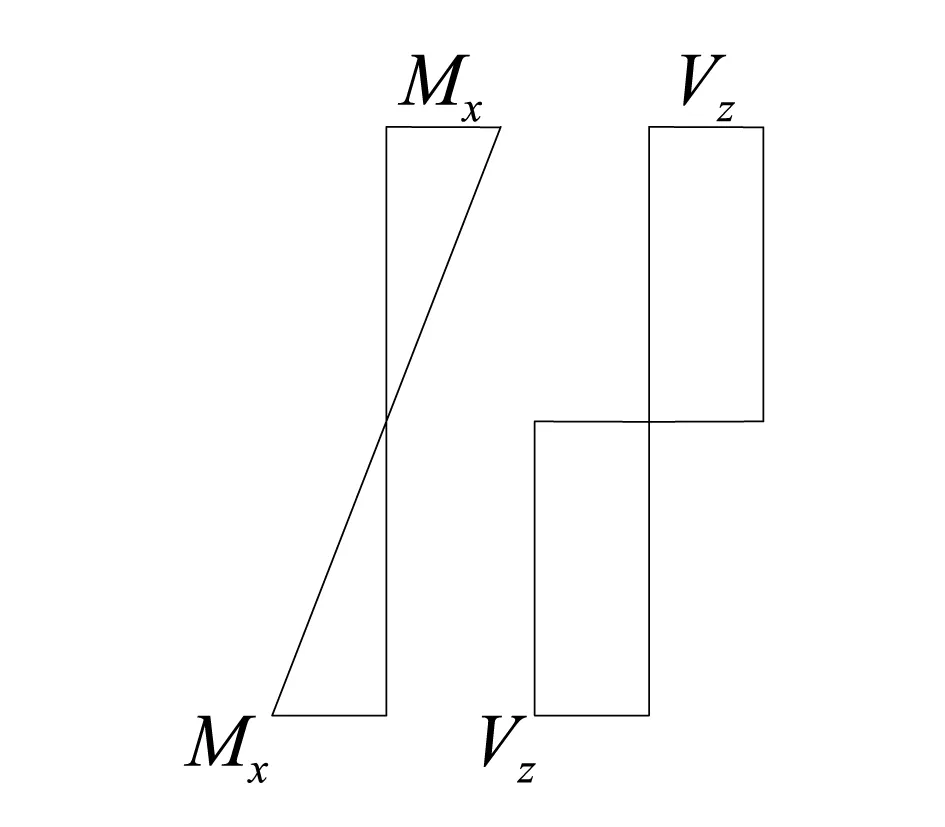
图5 内力图Fig.5 Internal force diagrams
1.2.1 初始刚度
根据结构力学中的力法来求解腹板的初始刚度。首先求其柔度,即单位力所产生的位移δ
(3)
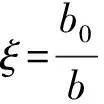
(4)
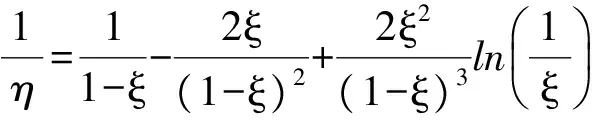
(5)
1.2.2 屈服位移
纯弯曲的应力计算公式为
(6)
当腹板高度为y处的某一截面的边缘(z=t/2)的应力达到屈服应力时,腹板进入屈服状态,则由式(6)可得此截面的屈服弯矩为
(7)
则此截面屈服时的曲率可由式(8)计算
(8)
由式(8)可见,沿y轴各个截面厚度相同处,截面屈服时的曲率都相同。则屈服位移为
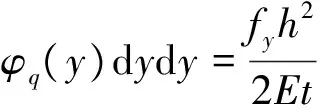
(9)
由式(8)可以看出,轴向拉压型金属阻尼器腹板在相同厚度处的各点同时达到屈服。
1.2.3 屈服荷载
一片X形腹板的屈服荷载为
(10)
考虑到本文中轴向拉压型金属阻尼器是由4组腹板对称布置在上下翼缘板与中心钢板之间,每组钢板由n片X形钢板组成,则计算轴向拉压型金属阻尼器整体刚度、屈服位移和屈服荷载时需对一片腹板相应的参数进行组合。
初始刚度为
(11)
(12)
屈服荷载为
(13)
屈服位移分别为
(14)
通过计算发现,当b0=0,即ξ=0时,η=1;当b0=b,即ξ=1时,η=1.5。所以当0≤ξ≤1时,1≤η≤1.5,随着b0的增加,腹板的初始刚度和屈服剪力也在增大。
2 轴向拉压型金属阻尼器抗震性能
利用轴向拉压型金属阻尼器理论计算式(12)~式(14),结合实测材性数据进行轴向拉压型金属阻尼器的初步设计,可以得到阻尼器初步外形尺寸,再通过有限元计算,可精确调整得到阻尼器尺寸参数。最终根据结构所需屈服刚度、屈服位移以及屈服荷载,选择符合参数要求的阻尼器尺寸为:耗能腹板选用4组,每组腹板采用3片X形钢板,腹板采用Q235钢,其他钢材均采用Q345钢,轴向拉压型金属阻尼器具体尺寸如图6所示。

图6 金属阻尼器构造Fig.6 Constructional detail of metallic damper
这种轴向拉压型金属阻尼器通过X形腹板的侧向弯曲屈服而耗能。它的最大优点在于相同厚度处的各点将同时达到屈服,充分发挥了钢板材料的塑性性能,大大提高了耗能能力。
《建筑抗震设计规范》规定消能部件的性能参数应经试验确定,通过对轴向拉压型金属阻尼器施加水平荷载进行低周反复拟静力试验,测试阻尼器的荷载-位移滞回性能,阻尼器的加载方式采用位移控制,加载工况为图7所示,试验装置如图8所示,加载作动器为MAS-100型作动器,最大出力100 kN,行程500 mm,位移采用拉线式位移计进行测量。
图9给出了阻尼器在不同工况下变形图。

图7 位移加载幅值Fig.7 Displacement amplitude of loading

图8 阻尼器试验Fig.8 Quasi-static test of the dampers
图10为根据拟静力试验得到的轴向拉压型金属阻尼器的滞回曲线。由图10可知,阻尼器滞回曲线呈饱满的反S形,没有颈缩和强度折减现象,说明阻尼器具有显著的能量吸收能力。根据试验数据得出的滞回曲线,可计算出阻尼器的初始刚度为3.22 kN/mm,屈服力为15.56 kN,屈服位移为4.87 mm。将阻尼器实际力学和几何参数代入理论式(12)~式(14),计算得出阻尼器的初始刚度为3.36 kN/mm,屈服力为15.36 kN,屈服位移为4.57 mm。计算结果表明理论计算结果与试验结果吻合较好,验证了拉压型金属阻尼器力学参数理论公式的正确性。

图9 不同位移下阻尼器变形Fig.9 Deformations of the damper under different displacement

图10 阻尼器滞回曲线Fig.10 Hysteretic loop curve of damper
3 EPSCF结构试验
此处所述EPSCF (External Prestressing Self-Centering)结构是一种新型抗震结构体系[7],如图11所示,该体系是在CR-RCF结构[8-10]基础上的改进,结构构造更简洁、施工更方便、预应力控制更准确。EPSCF结构具有以下技术特征:①在柱脚节点、梁柱节点处采用纯铰接的连接方式,使框架结构具有足够的转动能力,同时弱化了框架的整体刚度,减小了结构中地震输入的能量;②EPSCF结构采用体外预应力钢绞线提供地震作用下结构的自复位能力,在上下两层梁之间布置呈倒“八”或正“八”字形的钢绞线,张拉后产生预应力锚固于梁上、下表面;③结构中采用轴向拉压型金属阻尼器耗散地震能量、控制结构位移,结构的抗震性能得到显著提升。地震后,只需对摇摆节点部位装置及轴向拉压型金属阻尼器等进行必要的检查更换,无需进行结构构件本身的修复,地震后可很快恢复正常生活和生产,带来极明显的社会效益和经济效益,符合“可恢复功能”的抗震设计理念。

图11 EPSCF结构模型Fig.11 Model of EPSCF structure
为了进一步研究轴向拉压型金属阻尼器在建筑结构中的耗能减震作用,进行了EPSCF无控结构及EPSCF有控结构的对比试验。EPSCF有控结构是在EPSCF无控结构的基础上安装轴向拉压型金属阻尼器后形成,如图12所示。EPSCF有控结构中的轴向拉压型金属阻尼器在试验过程中发生屈服(见图13),控制了结构位移,耗散了输入到结构中的能量。

图12 EPSCF有控结构试验图Fig.12 Test of EPSCF structure with damper

图13 阻尼器变形图Fig13. Deformation of the damper
3.1 EPSCF结构耗能性能
根据EPSCF结构的拟静力试验,分别得到EPSCF无控结构及EPSCF有控结构的滞回曲线,如图14所示。

图14 EPSCF结构滞回曲线对比Fig.14 Comparison of hysteretic loop curves of EPSCF structures
由图14可知:①EPSCF无控结构的荷载位移曲线比较狭长,几乎呈一条直线,而EPSCF有控结构的荷载位移曲线呈饱满的反S形,说明EPSCF无控结构中钢绞线在摇摆过程中处于弹性,不具备耗能能力,而设置阻尼器的EPSCF有控结构具有显著的耗能能力;②EPSCF有控结构的层间位移达到6.94 mm时,结构中总荷载为17.57 kN。此时阻尼器屈服进入塑性变形阶段,开始发挥耗能作用,相应的阻尼器变形为5.04 mm、承担荷载为16.06 kN,初始刚度为3.25 kN/mm,而由理论式(12)~式(14)得出阻尼器参数为:初始刚度为3.36 kN/mm,屈服力为15.36 kN,屈服位移为4.57 mm。对比表明理论计算结果与EPSCF结构试验结果吻合较好。
在实际工程应用中,可以通过合理参数设计,当EPSCF结构遭遇多遇地震时,阻尼器保持弹性,为结构提供一定附加刚度,但不发挥耗能作用;当EPSCF结构经历设防烈度地震时,金属阻尼器发挥作用,X形腹板屈服耗能,耗散地震中的能量;当EPSCF结构进入罕遇地震阶段,应保证阻尼器不发生材料破坏,X形腹板不发生断裂。
将同方向加载的荷载-位移曲线中超过前一次加载最大荷载的区段平移相连后得到EPSCF无控结构及EPSCF有控结构的骨架曲线,如图15所示。
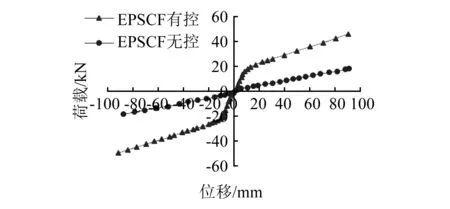
图15 EPSCF结构骨架曲线图Fig.15 Skeleton curves of EPSCF structures
由图15可知:①EPSCF有控结构曲线有明显的屈服点,呈现双折线的特征,而EPSCF无控结构几乎呈线性,主要由于EPSCF有控结构中阻尼器发生屈服,有明显的屈服点;②由于阻尼器结构本身具有一定的刚度,故EPSCF有控结构在第二阶段的刚度也比EPSCF无控结构大,即阻尼器的设置增加了结构刚度。
为探讨EPSCF无控与有控结构体系之间的关系,将EPSCF无控结构骨架曲线与阻尼器滞回曲线进行叠加(见图16(a)),并与EPSCF有控结构进行对比(见图16(b))

图16 EPSCF结构恢复力构成Fig.16 Restoring force components of EPSCF structure
图16可以看出,EPSCF无控结构与阻尼器的叠加曲线与EPSCF有控结构重合度较高,由此归纳出:EPSCF结构体系由预应力系统和阻尼系统线性叠加形成,其恢复力曲线关系如图17所示。图中预应力系统为线弹性,预应力的线性刚度为EPSCF无控结构试验结果中的刚度;阻尼系统的特征由结构中的阻尼器特性决定,根据阻尼器的滞回恢复力曲线,简化得到阻尼系统的骨架曲线。
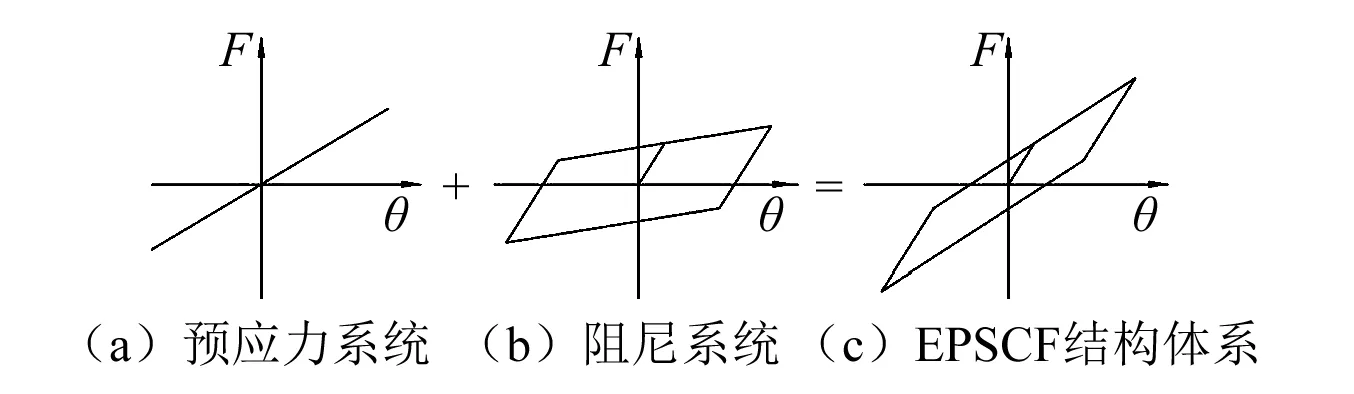
图17 EPSCF结构体系恢复力模型Fig.17 Restoring force model of EPSCF structures
3.2 轴向拉压型金属阻尼器耗能特性
将EPSCF无控结构、EPSCF有控结构及轴向拉压型金属阻尼器的滞回曲线进行对比,如图18所示。

图18 EPSCF结构及轴向拉压型金属阻尼器滞回曲线对比Fig.18 Comparison of hysteretic loop curves between EPSCF structures and axial compression-tension metallic damper
由图18可知:①EPSCF有控结构滞回曲线刚度大于EPSCF无控结构,说明了轴向拉压型金属阻尼器为结构提供了一定的刚度;②与EPSCF无控结构相比,EPSCF有控结构增加的耗能能力均来自阻尼器,说明轴向拉压型金属阻尼器作为建筑结构中的耗能装置效果显著。
在实际建筑中,要识别或用数学描述能量耗散(如摩擦、混凝土微裂缝的张开与闭合等)机理中的每一项似乎是不可能的[11]。因此,实际结构中的阻尼通常用高度理想化的方法描述。将实际结构中的阻尼用等效阻尼表示,是使用起来最简单的阻尼形式。根据《建筑抗震试验规程》[12](JGJ/T 101—2015)中关于结构或构件耗能性能的衡量要求,滞回曲线一个滞回环所围成的面积代表结构或构件耗能能力的大小。本文采用根据滞回曲线计算出的单周滞回耗能和等效阻尼系数ξe来判断试件的耗能能力。等效阻尼系数越大,则滞回曲线越饱满,面积越大;等效阻尼系数越小,耗能系数越小,则滞回曲线捏缩越严重。
如图19所示,面积ABCD为滞回曲线一周所耗散的能量;面积OBE为假想的弹性直线OB在达到相同位移(OE)时所包围的而积(即储存的弹性势能)。曲线面积ABC与三角形面积OBE之比,表示耗散能量与等效弹性体产生相同位移时输入的能量之比。等效阻尼系数的计算方法见式(15)。
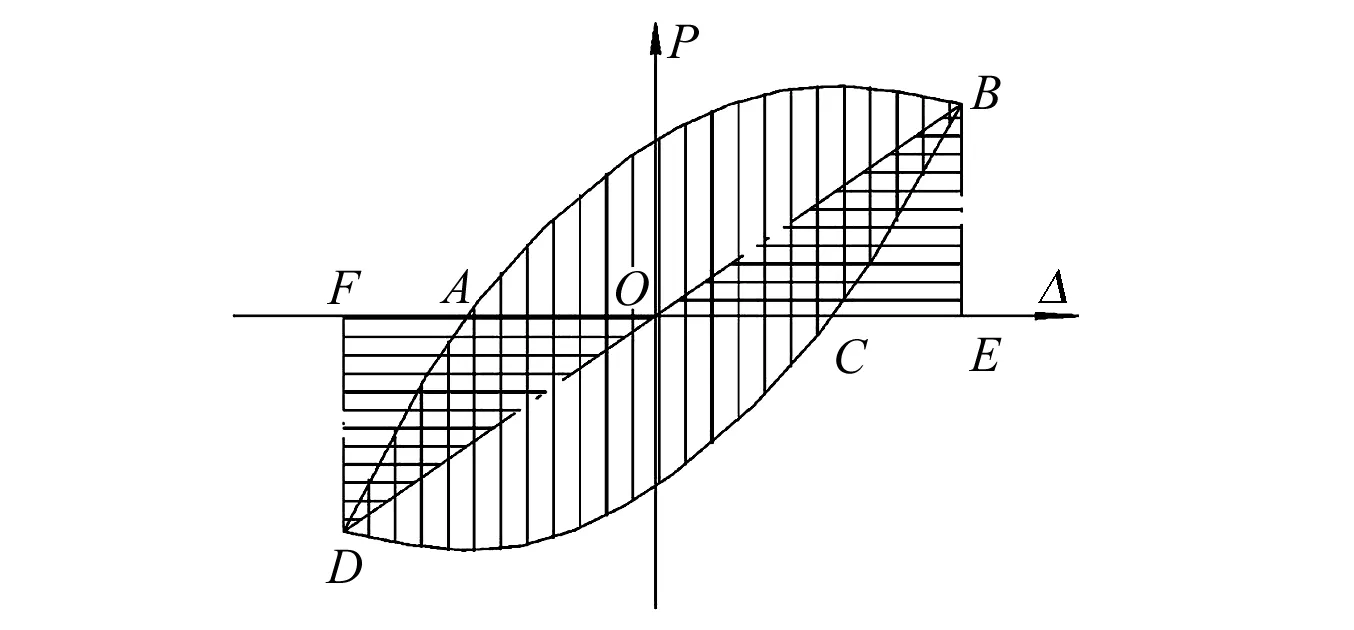
图19 荷载-位移滞回曲线Fig.19 Load-displacement hysteretic loop curve
(15)
从以上耗散能量(见图20)和等效阻尼系数(见图21)的对比可以看出:
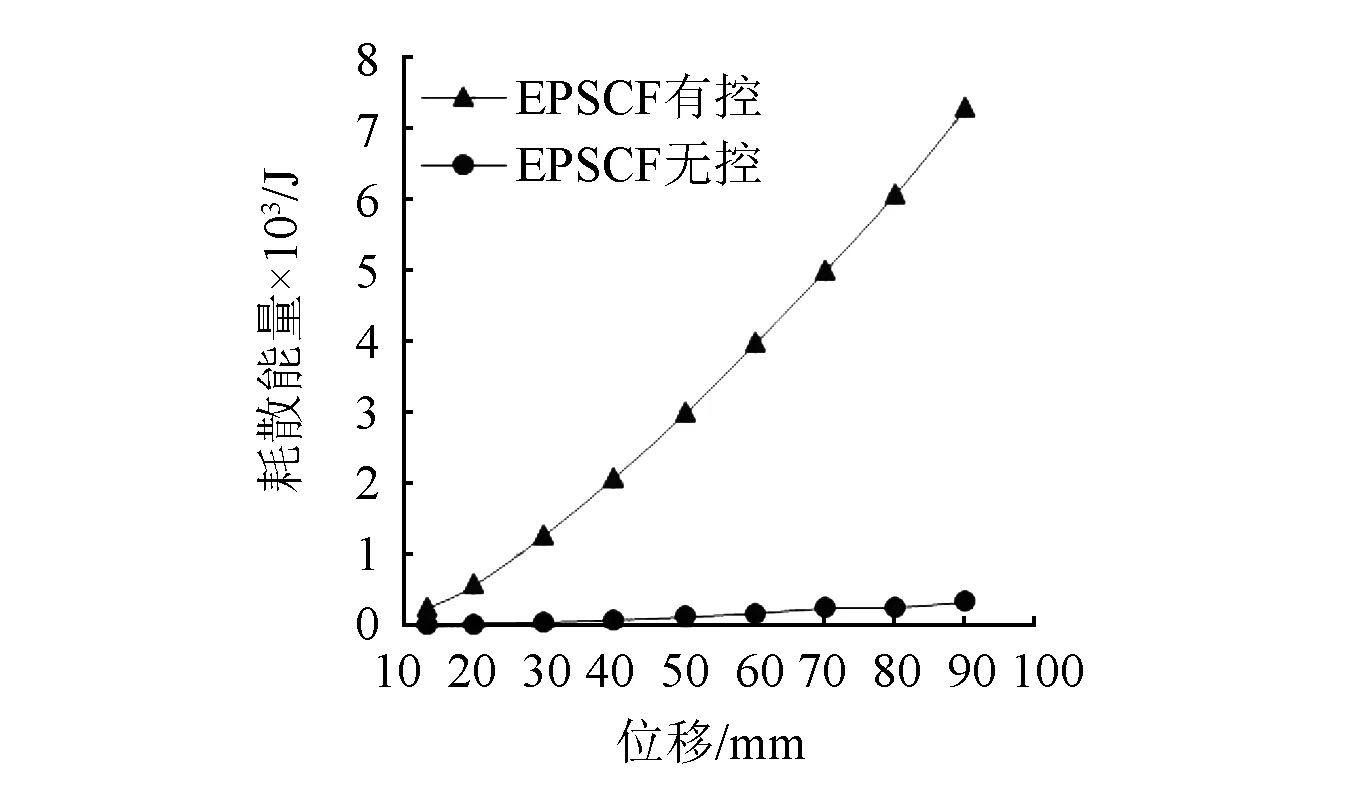
图20 EPSCF结构耗散能量图Fig.20 Energy dissipation diagram of EPSCF structures
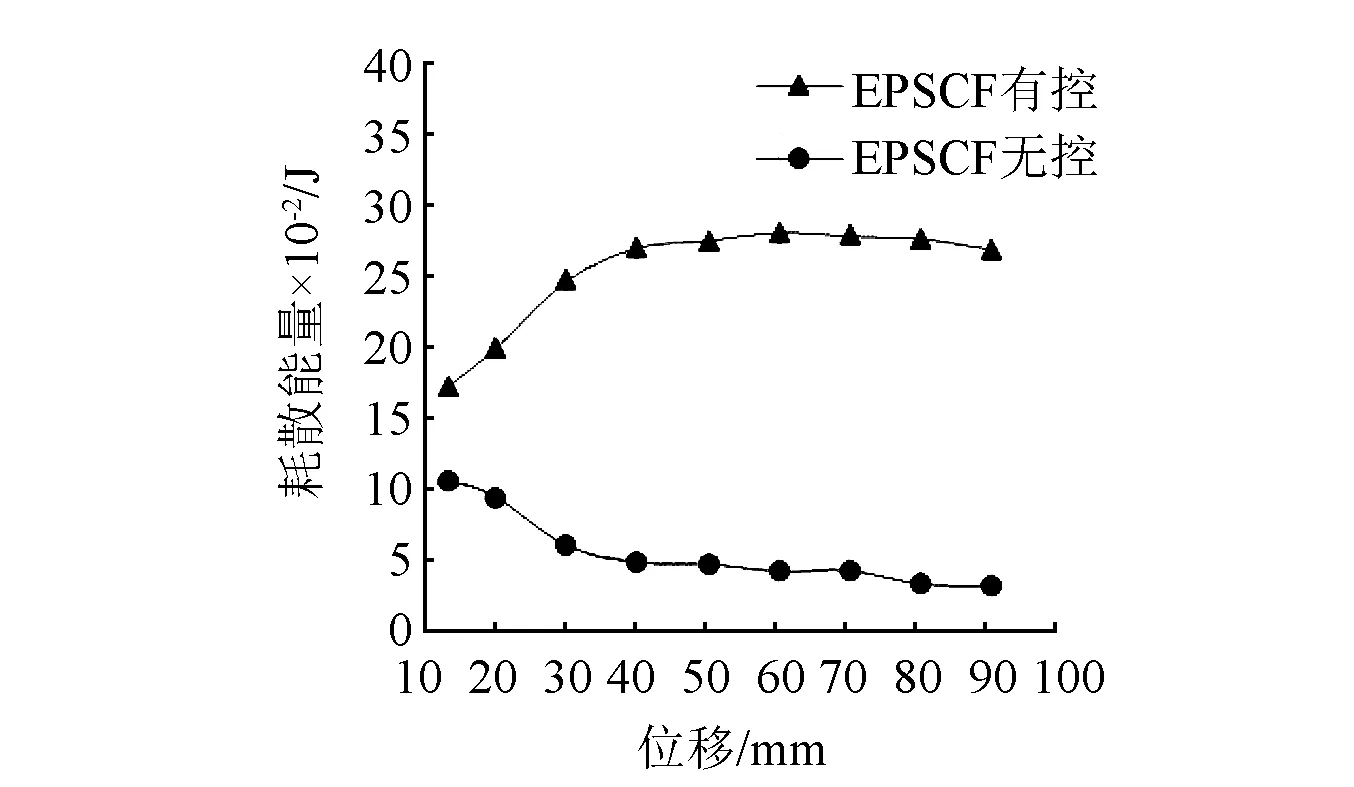
图21 等效阻尼系数Fig.21 Coefficient of equivalent damping
(1)对于安装轴向拉压型金属阻尼器的EPSCF有控结构,滞回环饱满,表现出良好的耗能特性。滞回耗能逐级增加,并且增加幅度在提高,在发生90mm位移时结构中耗散能量7 187J,是EPSCF无控结构耗能能力的20倍,这一特点和轴向拉压型金属阻尼器自身性能相关,说明了轴向拉压型金属阻尼器显著的耗能能力。
(2)安装轴向拉压型金属阻尼器的EPSCF有控结构,等效阻尼比呈先上升后略有下降的趋势,结构最初等效阻尼比为16.8%,当结构发生60mm位移时,等效阻尼比达到最大,且最大值为27.4%,之后等效阻尼系数略有降低,试验结束时等效阻尼比最终为26.2%;没有安装轴向拉压型金属阻尼器的EPSCF无控结构,等效阻尼系数比较小,当结构发生屈服位移后的第一个滞回环的等效阻尼系数为10.4%,随后等效阻尼比呈减小趋势,在结构发生90mm位移时,EPSCF无控结构等效阻尼比为3.2%,与EPSCF有控结构的26.2%相比,降低了87.8%,说明了轴向拉压型金属阻尼器具有稳定的耗能能力。
4 结 论
本文对轴向拉压型金属阻尼器及其应用在EPSCF结构中的抗震性能进行了试验研究,得出以下结论:
(1)轴向拉压型金属阻尼器利用腹板轴向拉压耗能,安装方式与黏滞阻尼器相同,安装方便、易于更换;在结构往复运动过程中对梁底不发生挤压,避免了引起结构构件局部损坏。
(2)轴向拉压型金属阻尼器滞回曲线呈饱满的反S形,没有颈缩和强度折减现象,说明轴向拉压型金属阻尼器具有显著的能量吸收能力。
(3)EPSCF结构体系由钢绞线系统和阻尼系统线性叠加形成,阻尼系统的特征由结构中的轴向拉压型金属阻尼器性能参数决定。
(4)大位移阶段,EPSCF无控结构的等效阻尼系数稳定在3.2%,设置轴向拉压型金属阻尼器的EPSCF有控结构等效阻尼系数为26.2%,说明轴向拉压型金属阻尼器具有稳定的耗能能力。
[ 1 ] 谢礼立,马玉宏. 现代抗震设计理论的发展过程 [J]. 国际地震动态,2003(10):1-8. XIE Lili, MA Yuhong. The development process of the modern earthquake resistant design theory [J]. Recent Developments in World Seismology, 2013(10):1-8.
[ 2 ] 周锡元,阎维明,杨润林. 建筑结构的隔震、减振和振动控制 [J]. 建筑结构学报,2002,23(2): 2-12. ZHOU Xiyuan, YAN Weiming, YANG Runlin. Seismic base isolation, energy dissipation and vibration control of building structures [J]. Journal of Building Structures, 2002,23(2):2-12.
[ 3 ] 周福霖,张颖,谭平. 层间隔震体系的理论研究 [J]. 土木工程学报, 2009,42(8):1-8. ZHOU Fulin, ZHANG Ying, TAN Ping. Theoretical study on story isolation system [J]. Civil Engineering Journal, 2009, 42(8):1-8.
[ 4 ] 赵鸿铁,徐赵东,张兴虎. 耗能减震控制的研究、应用与发展 [J]. 西安科技大学学报, 2001,33(1):1-6. ZHAO Hongtie, XU Zhaodong, ZHANG Xinghu. Study, application and development of energy dissipation and damping control [J]. Journal of Xi’an University of Architecture and Technology, 2001, 33(1):1-6.
[ 5 ] 徐培蓁, 潘鹏, 叶列平. 剪切型金属弯曲耗能阻尼器CN201485988U[P]. 2010-05-26.
[ 6 ] 鲁亮,罗检文. 一种轴向拉压型金属屈服耗能阻尼器:ZL 201520311435.8 [P]. 2015-11-11.
[ 7 ] LIU Xia, LU Liang, LU Xilin. Research on the seismic performance of an externally prestressed reinforced concrete frame [C]∥ Proceedings of the 6th International Conference on Advances in Experimental Structural Engineering.Urbana: Applied Mechanics and Materials,2011.
[ 8 ] LU Liang, LU Xilin, ZHU F B, et al. Experimental study on seismic performance of a controllable rocking reinforced concrete frame [C]∥ Proceedings of the 5th International Conference on Advances in Experimental Structural Engineering, Taipei:[s.n.], 2013.
[ 9 ] 鲁亮,江乐,李鸿,等. 柱端铰型受控摇摆式钢筋混凝土框架抗震性能的振动台试验研究[J]. 振动与冲击, 2016, 35(4): 193-198. LU Liang, JIANG Le, LI Hong, et al. Shaking table test study on the seismic performance of a controllable rocking reinforced concrete frame with column-end-hinge joints [J]. Journal of Vibration and Shock, 2016, 35(4): 193-198.
[10] 鲁亮,李鸿,刘霞,等. 梁端铰型受控摇摆式钢筋混凝土框架抗震性能的振动台试验研究[J]. 建筑结构学报, 2016, 37(3): 59-66. LU Liang, LI Hong, LIU Xia, et al. Shaking table test on seismic performance of controlled rocking reinforced concrete frame [J]. Journal of Building Structures, 2016, 37(3): 59-66.
[11] CHOPRA A K. 结构动力学理论及其在地震工程中的应用 [M].谢礼立,吕大刚,译.北京:高等教育出版社,2007.
[12] 建筑抗震试验方法规程:JGJ 101-96 [S]. 北京:中国建筑工业出版社,1997.
An experimental study on the mechanical properties of an axial compression-tension metallic damper and its application
LU Liang1, LIU Xia2, DAI Guixia1
(1. Research Institute of Structural Engineering and Disaster Reduction, Tongji University, Shanghai 200092, China; 2. International Institute for Urban Systems Engineering, Southeast University, Nanjing 210096, China)
The constructional detail and theoretical calculation of a kind of axial compression-tension metallic damper were introduced. The yield displacement, yield load and yield stiffness of the axial compression-tension metallic damper were obtained through the quasi-static test, and its energy dissipation capacity was analysed. The application of the damper used in External Prestressing Self-centering Frame (EPSCF) was researched. The results indicate that ① the axial tension-compression metallic damper dissipates energy through the deformation of its web plates, and the damages occurred on the adjacent components can be avoided; ② the installation type of this metallic damper is the same as the viscous damper, it can be conveniently installed and easily replaced; ③ the axial compression-tension metallic damper has the advantages of promoting additional stiffness, controlling drifts and dissipating seismic energy.
axial compression-tension metallic damper; seismic performance; quasi-static test; energy dissipation capacity
国家自然科学基金项目(51678453;51261120377)
2016-04-08 修改稿收到日期: 2016-07-08
鲁亮 男,博士,副教授,1969年11月生
刘霞 女,硕士,1990年7月生
TU352.1;TU317.1
A
10.13465/j.cnki.jvs.2017.16.022
