RC柱侧向冲击破坏模式的数值模拟研究
2017-08-31罗旗帜蒋志刚
刘 飞,罗旗帜,严 波,蒋志刚
(1.湖南大学 土木工程学院,长沙 410082;2. 国防科技大学 指挥军官基础教育学院,长沙 410073)
RC柱侧向冲击破坏模式的数值模拟研究
刘 飞1,2,罗旗帜1,严 波2,蒋志刚2
(1.湖南大学 土木工程学院,长沙 410082;2. 国防科技大学 指挥军官基础教育学院,长沙 410073)
采用非线性有限元方法对有轴压力RC柱的动态响应过程进行了数值仿真,分析了RC柱的破坏模式及其转换机理,研究了轴压力的影响。结果表明:有轴压力RC柱剪切破坏过程可分为斜裂缝形成、箍筋屈服和完全破坏三个阶段,其变形模式先后为撞击点局部弯曲、整体弯曲和柱子根部局部剪切变形;静力条件下弯曲破坏RC柱在冲击作用下可能发生剪切破坏,其重要原因是纵筋应变率大于箍筋应变率;随着轴压比的增大,发生剪切破坏的RC柱趋向于发生由混凝土抗压强度控制的弯曲破坏。
RC柱;冲击;数值模拟;破坏模式;应变率效应
钢筋混凝土(Reinforced Concrete,RC)结构在土木工程中已得到广泛应用。这些结构在其全寿命周期内,可能遭受爆炸[1]和撞击[2]等冲击作用。RC梁在冲击作用下的动力响应问题已有较多研究[3-7]。RC柱是桥梁和建筑结构中最重要的构件之一,其损伤或破坏可能导致结构的局部或整体垮塌,造成灾难性后果。田力等[8]对刚性球侧向撞击RC柱的动态响应和破坏模式进行了数值模拟研究,分析了刚性球质量与初速度、混凝土轴心抗压强度、配筋率等参数的影响。陈海彬等[9]基于拉格朗日方程对RC柱在侧向冲击作用下的动力反应模式进行了分析,建立了单自由度模型动力反应计算公式。上述研究均忽略了轴压力对RC柱动力响应及破坏模式的影响。在工程结构中,RC柱通常承受较大轴压力,需考虑轴压力的影响。Wang等[10]对有轴压力的两端简支RC柱在侧向冲击荷载下的动力响应进行了试验研究,分析了加载速率、纵筋配筋率和箍筋配筋率对破坏模式和承载能力的影响。Sha等[11]采用摆锤加载装置对有轴压力的RC圆柱缩比桥墩柱进行了侧向冲击试验,分析了冲击速度、桥墩直径、桥墩高度、冲击位置和冲击质量的影响。Loedolff[12]采用摆锤加载方式对有轴压力的RC悬臂柱进行了侧向冲击试验,研究了配筋率、混凝土强度和轴压力的影响。但上述研究并未深入分析轴压力对破坏模式的影响。
RC柱在侧向冲击作用下主要有正截面弯曲破坏和斜截面剪切破坏两种模式[13]。试验表明,在冲击荷载作用下,静力荷载下发生弯曲破坏的RC柱可能发生剪切破坏,但对其原因尚无研究。剪切破坏属于脆性破坏,易造成灾难性后果。在设计中,通常通过增加箍筋配筋率来防止剪切破坏[14]。然而,冲击作用下弯曲破坏与剪切破坏的转换条件不同于静力作用。因此,深入研究冲击作用下的破坏模式转换机理对RC柱的抗冲击设计具有重要意义。
本文采用非线性有限元方法,对侧向冲击作用下有轴压力RC柱的破坏过程进行模拟,重点分析了RC柱的剪切破坏过程,揭示了破坏模式的转换机理,并研究了轴压力对破坏模式的影响。
1 有限元模型及验证
为验证本文数值模拟方法的可靠性,对Loedolff试验的典型工况进行了数值模拟。
1.1 试验简介
Loedolff共开展了8组36个试验,试验装置如图1所示。本文选取工况8A和工况8D为模拟验证工况,两工况试件除混凝土强度略有差别以外,其余均相同。其中,工况8A为静载加载,在柱子根部发生弯曲破坏;工况8D为冲击加载,在柱子下部区域发生剪切破坏。RC柱为矩形截面(350 mm×150 mm),高1 600 mm。纵向主筋为变形钢筋,直径16 mm,屈服强度518.6 MPa,弹性模量207.22 GPa;箍筋为光面钢筋,直径8 mm,间距150 mm,屈服强度376.3 MPa,弹性模量202.69 GPa。工况8A的混凝土单轴压缩强度(28天龄期)为23.96 MPa,工况8D为27.55 MPa。混凝土保护层均为23 mm。
RC柱通过底座与钢制基础实现固定连接(见图1),底座高400 mm,截面尺寸630 mm×150 mm。轴压力通过RC柱顶部的加载梁进行加载,加载梁在水平方向无约束,轴压力均为100 kN。撞击体组成如图2所示,通过铅板进行配重,总质量为850 kg。为模拟车辆撞击过程,在撞击体头部安装有特殊设计的缓冲部件。缓冲部件由8根钢管组成,钢管内径和外径分别为41.1 mm和48.8 mm。工况8D的冲击速度为7.091 m/s,缓冲部件的最终压溃变形量为100 mm。
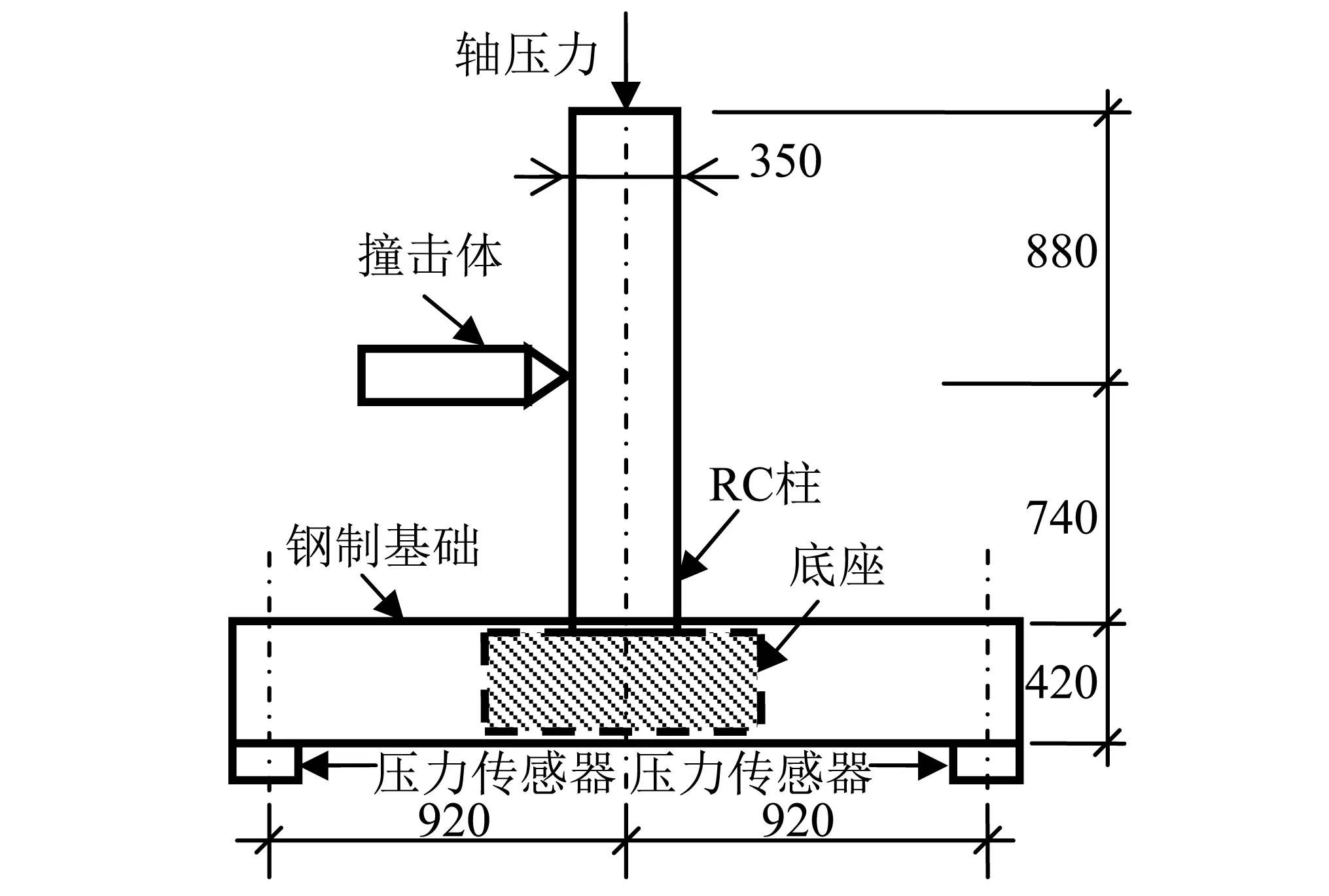
图1 试验装置(单位:mm)Fig.1 Experiment set-up (unit:mm)

图2 撞击体组成示意图Fig.2 Schematic diagram of striker
1.2 有限元模型
本文采用LS-DYNA非线性有限元分析软件。有限元模型如图3所示,共划分为83 570个单元。混凝土、撞击体和钢板均采用Solid164单元进行网格划分,缓冲部件采用Shell163单元,纵向主筋采用Beam161单元,箍筋采用Link160单元。

图3 有限元模型Fig.3 FE model
对底座侧面和底面施加固定约束。缓冲部件和RC柱之间采用面-面侵蚀接触算法,钢筋与混凝土之间采用CONSTRAINED_LAGRANGE_IN_SOLID算法[15]进行模拟,不考虑钢筋与混凝土之间的黏结失效。为简化建模,轴压力通过钢板均匀施加,以避免集中加载引起沙漏模式。
混凝土采用CSCM材料模型。该模型适用于混凝土的低速冲击问题[16],可根据混凝土单轴压缩强度自动计算材料参数,应用十分方便。CSCM模型的材料屈服面基于3个应力不变量,如式(1)~式(3)所示。
(1)
Ff(J1)=α-λexp-βJ1+θJ1
(2)
(3)

混凝土损伤由归一化损伤变量d表示,d值的变化范围为0~1。当单元应变能低于损伤阈值时,混凝土单元没有损伤,d值为0;当单元应变能大于损伤阈值时,混凝土单元出现损伤并逐渐累积,d值不断增大;当d=0.999时,混凝土单元发生完全破坏。由于发生完全损伤的混凝土单元已丧失继续承载能力,导致其变形迅速增大,可能引起单元过度畸变。为克服单元畸变所引起的计算不稳定,可将变形较大的完全损伤混凝土单元进行删除。本文采取损伤变量和最大主应变双重控制准则,当同时满足损伤变量等于0.999和最大主应变大于0.3两个条件时,该混凝土单元将被删除。
钢材采用MAT_PLASTIC_KINEMATIC材料模型。该模型采用双线性应力应变曲线,可考虑各向同性硬化、随动硬化和应变率效应。应变率效应基于Cowper-Symonds模型,如式(4)所示。
(4)

混凝土单轴压缩强度、钢筋屈服应力和弹性模量取值均与Loedolff的实测值一致。此外,钢筋泊松比取为0.3,塑性模量取为1.5 GPa[17],应变率参数C和P分别取为40.4和5[18]。
1.3 有限元模型的验证
图4给出了工况8A的荷载-位移曲线。位移测量点为1/2柱高截面。可见,本文模拟结果与试验结果吻合较好。在水平静载作用下,试验RC柱发生弯曲破坏,屈服荷载的试验值约为100 kN,本文数值模拟约为104 kN,相对误差为4%。
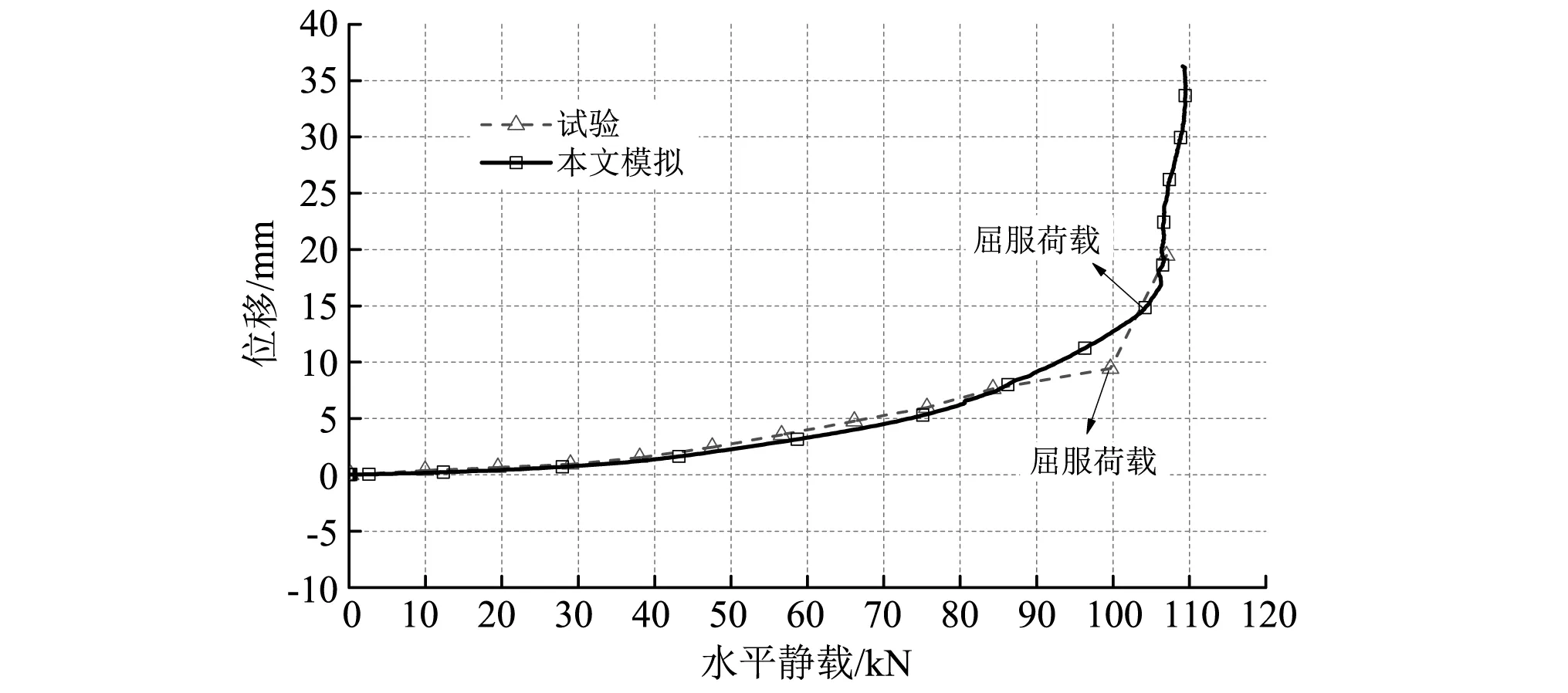
图4 荷载-位移曲线(工况8A)Fig.4 Load-displacement curve(column 8A)
图5为工况8D的裂纹/损伤分布情况对比。可见,数值模拟准确模拟了试件的剪切破坏现象,在试件底部区域产生了一条贯通的斜裂缝,裂纹/损伤分布与试验结果基本吻合。
图6和图7分别为工况8D的冲击力和缓冲部件变形量时程曲线。可见,冲击力的数值模拟结果与试验结果基本吻合;缓冲部件变形量模拟值为99.1mm,与试验值(100mm)的相对误差仅为0.9%。

图5 裂纹/损伤分布(工况8D)Fig.5 Cracking/damage patterns(column 8D)

图6 冲击力时程曲线(工况8D)Fig.6 History of impact forces(column 8D)
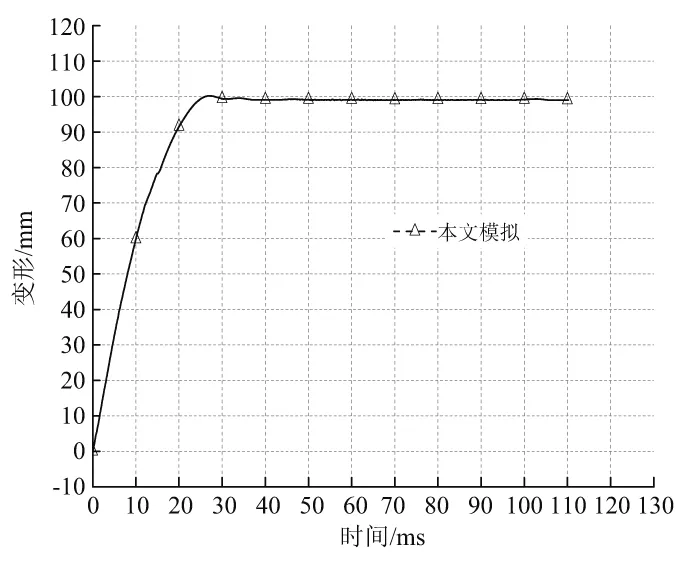
图7 缓冲部件变形(工况8D)Fig.7 Deflection of buffer(column 8D)
综上可知,本文有限元模型及采用的材料模型、单元类型、接触算法、计算控制方法等较为合理,能够准确模拟有轴压力RC柱的破坏过程。
2 响应过程及破坏模式转换机理
2.1 损伤过程分析
基于工况8D的计算结果,对有轴压力RC柱的冲击破坏过程进行分析。为便于描述,图8给出了相关特征单元的位置示意图。其中,S1、S2为试件底部的纵向主筋单元,S3、S4为主斜裂缝位置的箍筋单元,S5为撞击点高度处的纵向主筋单元,C1、C2为主斜裂缝位置的混凝土单元,C3、C4为试件底部的混凝土单元。
图9为工况8D的损伤发展过程。当t≤3ms时,被撞点背面的混凝土裂缝已基本出齐,迎撞面根部出现一条水平裂缝和两条斜裂缝;当3ms

图8 特征单元位置示意图Fig.8 Location of typical elements

图9 混凝土损伤发展过程Fig.9 Propagation of concrete damage
图10为混凝土单元C1、C2的最大主应力时程曲线。当t<8.8ms时,混凝土单元C1、C2的最大主应力迅速增大,达到抗拉强度后下降为0。值得注意的是,混凝土单元C1、C2的最大主应力曲线均呈现出一定程度的波动。尤其是混凝土单元C2,其最大主应力在2~3ms时迅速下降,在3~3.5ms时明显上升。其原因在于撞击过程中的应力波作用和混凝土损伤所引起的应力重分布。当斜裂缝发展至C2单元之后(图9(b),t≥3.5ms),其最大主应力随损伤发展而再次下降,直至为0。
图11为混凝土单元C3、C4的最大主应力时程曲线。受拉侧混凝土单元C3在约0.4ms时即已达到拉应力峰值,在约1ms时发生拉伸破坏;而受压侧混凝土单元C4在约1.4ms时达到压应力峰值,在约25ms时发生压溃破坏。
图12为箍筋单元S3、S4的轴向应力时程曲线。从图中可以看出,箍筋单元S3、S4分别在8.8ms和16.4ms发生了屈服,屈服强度分别为375MPa和376MPa。
由图6、图9~图12,可将RC柱的剪切破坏过程划分为斜裂缝形成、箍筋屈服和完全破坏三个阶段。在斜裂缝形成阶段(t<8.8ms),混凝土单元在最大主应力作用下发生拉伸破坏,主斜裂缝基本形成。在箍筋屈服阶段(8.8ms≤t<25.7ms),箍筋单元相继发生屈服,主斜裂缝的损伤程度不断增大,受压区混凝土发生局部压溃破坏。在完全破坏阶段(t≥25.7ms),主斜裂缝的损伤快速增大,与受压区损伤相互贯通,形成贯穿斜裂缝,冲击力迅速下降(见图6),RC柱发生完全破坏。
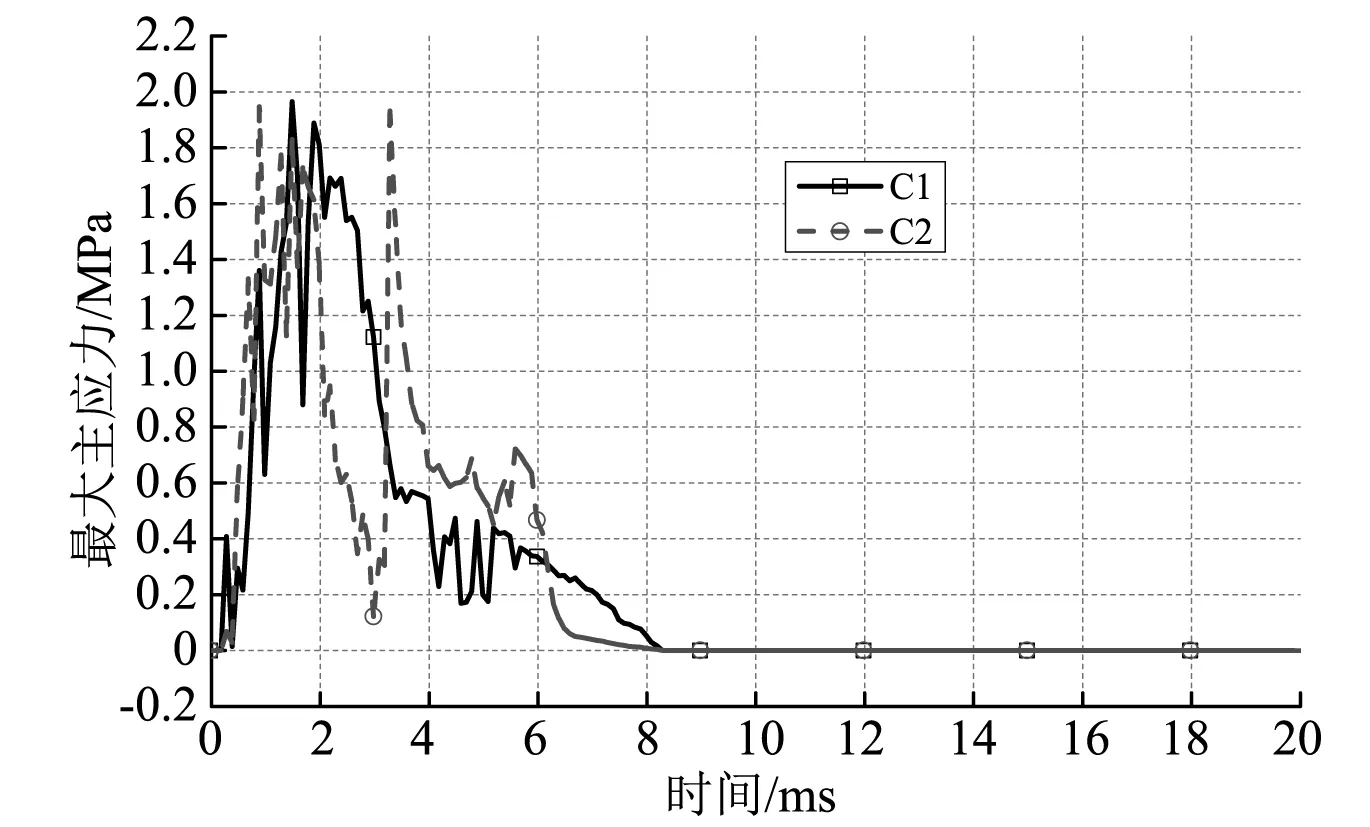
图10 混凝土单元C1、C2的最大主应力Fig.10 Maximum principal stress of C1 and C2

图11 混凝土单元C3、C4的最大主应力Fig.11 Maximum principal stress of C3 and C4
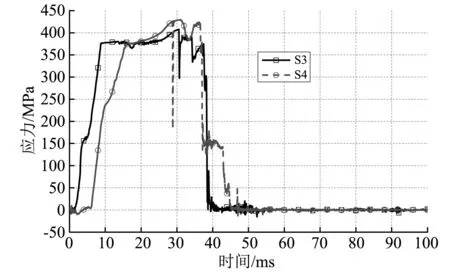
图12 箍筋单元S3、S4的轴向应力Fig.12 Axial stress of S3 and S4
2.2 变形过程分析
图13为典型时刻RC柱的中轴线水平位移情况,图14为纵筋单元S1、S2和S5的轴向应力时程曲线。在斜裂缝形成阶段(t<8.8ms),当t≤3ms时,RC柱主要发生局部弯曲变形,最大变形位置位于撞击点,纵筋单元S1、S2和S5的轴向应力从撞击初始时刻即开始明显增大,箍筋单元S3、S4分别从1.5ms和6ms开始明显增加(见图12);随后,RC柱发生整体弯曲变形,纵筋单元S1的轴向应力持续增大,S5单元出现卸载,柱子根部开始产生局部剪切变形。在箍筋屈服阶段(8.8ms≤t<25.7ms),受拉侧箍筋单元S3首先发生屈服(t=8.8ms),柱子根部的局部剪切变形明显增大,之后弯曲变形基本消失,S1、S4、S2单元相继在12ms、16.4ms、18.4ms时刻发生屈服,S5单元的轴向应力维持在较低水平。在完全破坏阶段(t≥25.7ms),柱子根部的局部剪切变形迅速增大,受拉侧纵筋单元S1发生卸载,受压侧纵筋单元S2和箍筋单元S3、S4的轴向应力由于应变硬化效应而继续增大,直至RC柱发生完全破坏。由此可见,在RC柱冲击剪切破坏过程中,其变形模式从撞击初期的撞击点局部弯曲变形迅速转变为整体弯曲变形,最后转变为以柱子根部的局部剪切变形为主而发生剪切破坏。
2.3 破坏模式转换机理
Loedolff的试验表明,工况8A(静载作用)的破坏模式为弯曲破坏,而工况8D(冲击作用)的破坏模式为剪切破坏。两者试件除混凝土强度略有差别以外,其余均相同。相对于静载作用而言,冲击作用下结构响应的显著特征是材料应变率效应和惯性效应。有关惯性效应对破坏模式的影响,Cotsovos等已进行了研究。下面从材料应变率效应方面进行分析。
从图10和图11可以看出,混凝土单元在斜裂缝形成阶段(t<8.8ms)即已达到应力峰值,单元C1、C2和C3均发生完全破坏,单元C4进入软化阶段。由于应变率效应,混凝土单元的强度有所提高。但此时RC柱远未达到其抗力峰值,因此高应变率所引起的混凝土强度提高对RC柱抗力的影响较小。
图15为纵筋单元S1和箍筋单元S3的应变率时程曲线。从图中可以看出,在RC柱发生完全破坏之前,箍筋单元S3在屈服时(t=8.8ms)的应变率较低(1.73×10-4s),屈服强度的提高幅度很小,约为3%(见图12);而纵筋单元S1在屈服时(t=12ms)的应变率较高(0.932s),导致纵筋屈服强度增加幅度较大,约为54%(见图14)。在屈服发生时,纵筋的应变率远大于箍筋,纵筋的屈服强度提高幅度大于箍筋,这就导致了RC柱抗弯能力的提高幅度大于抗剪能力,进而使得RC柱在冲击作用下趋向于发生剪切破坏。
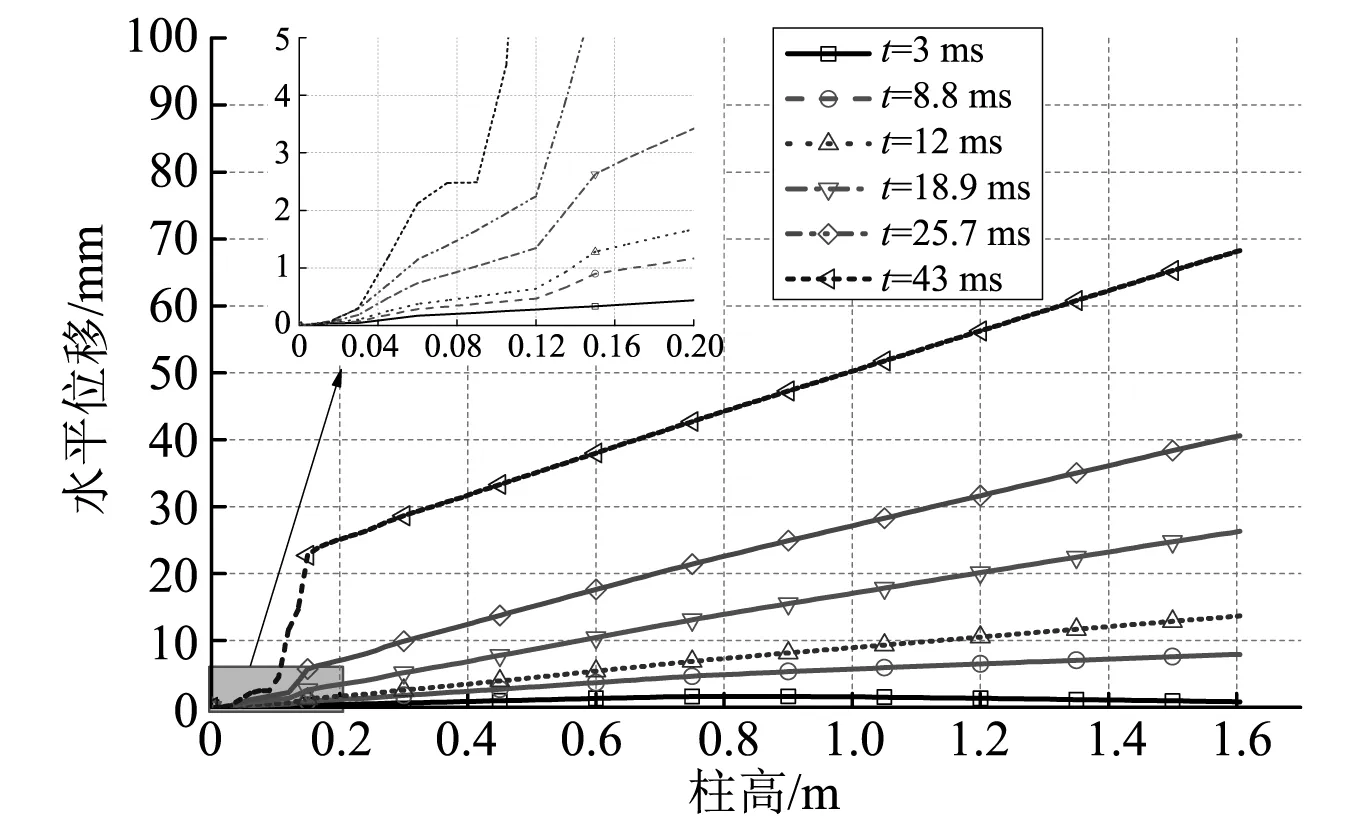
图13 RC柱的中轴线水平位移Fig.13 Horizontal displacement of RC column axis
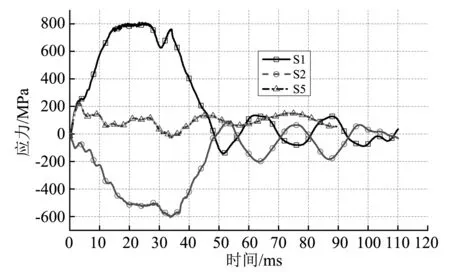
图14 纵筋单元S1、S2和S5的轴向应力Fig.14 Axial stress of S1, S2 and S5

图15 钢筋单元的应变率时程曲线Fig.15 History of strain rate of reinforcement elements
综上可知,纵筋应变率大于箍筋是RC柱由弯曲破坏模式转为剪切破坏模式的重要原因。
3 轴压力对破坏模式的影响
试验工况8D的轴压比为5.4%。另取轴压比分别为10.7%、16.1%、26.8%、37.6% 和48.3%进行模拟计算。各工况除轴压比不同以外,冲击速度、混凝土强度、配筋等条件均保持一致。
图16为不同轴压比RC柱的损伤情况,图17为受拉侧纵筋单元S1的轴向应力时程曲线。可见,随着轴压比的增大,RC柱的破坏模式发生了明显改变。当n0=5.4%时,RC柱发生剪切破坏,纵筋单元S1发生屈服;当n0=10.7%、16.1%和26.8%时,RC柱发生了严重损伤,但未发生完全破坏,背撞面根部的混凝土压溃区随轴压比增大而增大,纵筋单元S1发生屈服;当n0=37.6%和48.3%时,RC柱发生弯曲破坏,背撞面根部的混凝土完全压溃失效,纵筋单元S1尚未达到屈服。以上结果表明,随着轴压比增大,RC柱由剪切破坏模式转换为由混凝土抗压强度控制的弯曲破坏模式。

图16 RC柱的损伤情况(n0=5.4%~48.3%)Fig.16 Damage of RC columns(n0=5.4%-48.3%)

图17 纵筋单元S1的轴向应力时程曲线(n0=5.4%~48.3%)Fig.17 History of axial stress of S1 (n0=5.4%-48.3%)
4 结 论
本文采用非线性有限元方法对有轴压力RC柱的侧向冲击破坏过程进行了数值模拟,分析了RC柱的破坏模式及其转换机理,并研究了轴压力对破坏模式的影响。研究表明:有轴压力RC柱的剪切破坏过程可分为斜裂缝形成、箍筋屈服和完全破坏三个阶段,其变形模式先后为撞击点局部弯曲、整体弯曲和柱子根部局部剪切变形;纵筋应变率大于箍筋应变率是RC柱由弯曲破坏模式转换为剪切破坏模式的重要原因;随着轴压比的增大,RC柱由剪切破坏模式转换为由混凝土抗压强度控制的弯曲破坏模式。
[ 1 ] JAYASOORIYA R, THAMBIRATNAM D P, PERERA N J, et al. Blast and residual capacity analysis of reinforced concrete framed buildings[J].Engineering Structures,2011,33(12):3483-3495.
[ 2 ] SHARMA H, GARDONI P, HURLEBAUS S. Probabilistic demand model and performance-based fragility estimates for RC column subject to vehicle collision[J]. Engineering Structures, 2014, 74: 86-95.
[ 3 ] FUJIKAKE K, LI B, SOEUN S. Impact response of reinforced concrete beam and its analytical evaluation[J]. Journal of Structural Engineering, 2009,135(8): 938-950.
[ 4 ] COTSOVOS D M, STATHOPOULOS N D, ZERIS C A. Behavior of RC beams subjected to high rates of concentrated loading[J]. Journal of Structural Engineering, 2008, 134(12): 1839-1851.
[ 5 ] 赵德博,易伟建. 钢筋混凝土梁抗冲击性能和设计方法研究[J]. 振动与冲击, 2015,34(11): 139-145. ZHAO Debo, YI Weijian. Anti-impact behavior and design method for RC beams[J]. Journal of Vibration and Shock, 2015, 34(11): 139-145.
[ 6 ] 廖维张,张伟,田志敏. 高强钢绞线网-高性能砂浆加固钢筋混凝土梁抗冲击性能试验研究[J]. 振动与冲击, 2014, 33(12): 200-206. LIAO Weizhang, ZHANG Wei, TIAN Zhimin. Tests for
impact resistance properties of RC beams strengthened with high strength steel wire mesh and high performance mortar[J]. Journal of Vibration and Shock, 2014, 33(12): 200-206.
[ 7 ] ADHIKARY S D, LI B, FUJIKAKE K. Dynamic behavior of reinforced concrete beams under varying rates of concentrated loading[J]. International Journal of Impact Engineering, 2012, 47: 24-38.
[ 8 ] 田力, 朱聪, 王浩, 等.碰撞冲击荷载作用下钢筋混凝土柱的动态响应及破坏模式[J].工程力学,2013,30(2): 150-155. TIAN Li, ZHU Cong, WANG Hao, et al. Dynamic response and failure modes of RC columns under impact[J]. Engineering Mechanics, 2013,30(2):150-155.
[ 9 ] 陈海彬, 高静, 葛楠, 等. 钢筋混凝土柱在冲击荷载作用下破坏模式研究[J]. 建筑结构学报,2009(增刊2): 104-108. CHEN Haibin, GAO Jing, GE Nan, et al. Investigation on failure mode of RC members subjected to impulsive load[J]. Journal of Building Structures, 2009(Sup 2): 104-108.
[10] WANG X G, ZHANG Y M, SU Y P, et al. Experimental investigation on the effect of reinforcement ratio to capacity of RC column to resist lateral impact loading[J]. Systems Engineering Procedia , 2011,1: 35-41.
[11] SHA Y Y, HAO H. Laboratory tests and numerical simulations of barge impact on circular reinforced concrete piers[J]. Engineering Structures , 2013, 46: 593-605.
[12] LOEDOLFF M J. The behaviour of reinforced concrete cantilever columns under lateral impact load[D]. Stellenbosch: University of Stellenbosch, 1989.
[13] REMENNIKOV A M, KAEWUNRUEN S. Impact resistance of reinforced concrete columns: experimental studies and design considerations[C]// 19th Australasian Conference on the Mechanics of Structures and Materials. Abingdon: Taylor & Francis, 2006: 817-824.
[14] OŽBOLT J, SHARMA A. Numerical simulation of reinforced concrete beams with different shear reinforcements under dynamic impact loads[J]. International Journal of Impact Engineering , 2011,38: 940-950.
[15] MURRAY Y D. User manual for LS_DYNA concrete material model 159[R]. McLean: Federal Highway Administration, 2007.
[16] MURRAY Y D, ABU-ODEH A, BLIGH R. Evaluation of LS-DYNA concrete material Model 159[R]. McLean: Federal Highway Administration, 2007.
[17] REDDY T Y, REID S R. Phenomena associated with the crushing of metal tubes between rigid plates[J]. International Journal of Solids and Structures, 1980,16(6): 545-562.
[18] TANIMURA S, TSUDA T, ABE A, et al. Comparison of rate-dependent constitutive models with experimental data[J]. International Journal of Impact Engineering, 2014, 69: 104-113.
Numerical study on the failure mode of RC column subjected to lateral impact
LIU Fei1,2, LUO Qizhi1, YAN Bo2, JIANG Zhigang2
(1. College of Civil Engineering, Hunan University, Changsha 410082, China;2. College of Basic Education, National University of Defense Technology, Changsha 410073, China)
The dynamic responses of RC columns with axial loads subjected to lateral impact were simulated with the nonlinear finite element method. The failure mode and its transition mechanisms, the influences of axial loads were investigated. The results show that the shear failure process of RC columns can be divided into three stages, i.e., diagonal cracks development, transverse reinforcement yield, and global failure. The deformation mode has gone through the local flexural deformation, the overall flexural deformation, and the local shear deformation successively. RC columns which failed in flexure under static load would fail in shear under impact load; one of the important reasons was the different strain rates between main reinforcement and transverse reinforcement. The strain rate of main reinforcement was greater than that of transverse reinforcement. RC columns tended to fail in flexure which was controlled by compressive strength of concrete with increase of axial load ratio.
RC columns; impact; numerical simulation; failure modal transition; strain rate effects
国家自然科学基金(50978058);全国优秀博士学位论文作者专项资金资助项目(200954);广东省交通运输厅科技资助项目(2012-02-018)
2016-03-15 修改稿收到日期: 2016-06-20
刘飞 男,博士生,讲师,1982年生
罗旗帜 男,博士,教授,1955年生
O347.1;TU375.1
A
10.13465/j.cnki.jvs.2017.16.019
