欠约束多机协调吊运系统工作空间和运动稳定性分析
2017-08-31王砚麟赵志刚李劲松
王砚麟, 赵志刚, 苏 程, 李劲松, 季 钢
(1. 兰州交通大学 机电工程学院, 兰州 730070; 2. 上海交通大学 机械与动力工程学院, 上海 200030)
欠约束多机协调吊运系统工作空间和运动稳定性分析
王砚麟1, 赵志刚1, 苏 程1, 李劲松2, 季 钢2
(1. 兰州交通大学 机电工程学院, 兰州 730070; 2. 上海交通大学 机械与动力工程学院, 上海 200030)
主要针对多机器人协调吊运系统的工作空间和运动稳定性进行分析,根据吊运系统驱动配置情况将系统分为3类;其次应用牛顿欧拉方程建立了系统的广义动力学模型;采用虚拟柔索法给出了该欠约束系统力旋量封闭的解决方案,并对系统工作空间进行了分析,依据广义逆矩阵理论给出了系统满足运动要求时柔索拉力的最优解;根据克拉索夫斯基法给出了吊运系统的运动稳定性判据;根据实例参数,对3类系统的工作空间进行了数值仿真分析,并应用方阵特征值分解法对工作空间中所有点的稳定性进行了计算。结果表明,3类系统在各自工作空间内均是稳定的,并获得了3类系统的稳定程度关系,研究结果为后续优化系统运动轨迹规划和防摆控制打下基础。
吊运系统;多机器人系统;广义动力学模型;工作空间;稳定性分析
与传统刚性并联机器人相比,柔索式多机器人协调吊运系统具有结构简单、工作空间大、负载能力强、运动速度快、模块化程度高、运动灵活且精度高以及系统柔性好等优点[1-4],这使柔索式多机器人协调吊运系统在工程应用中得以重用,因此对该类系统的研究具有重要的理论和工程应用价值。
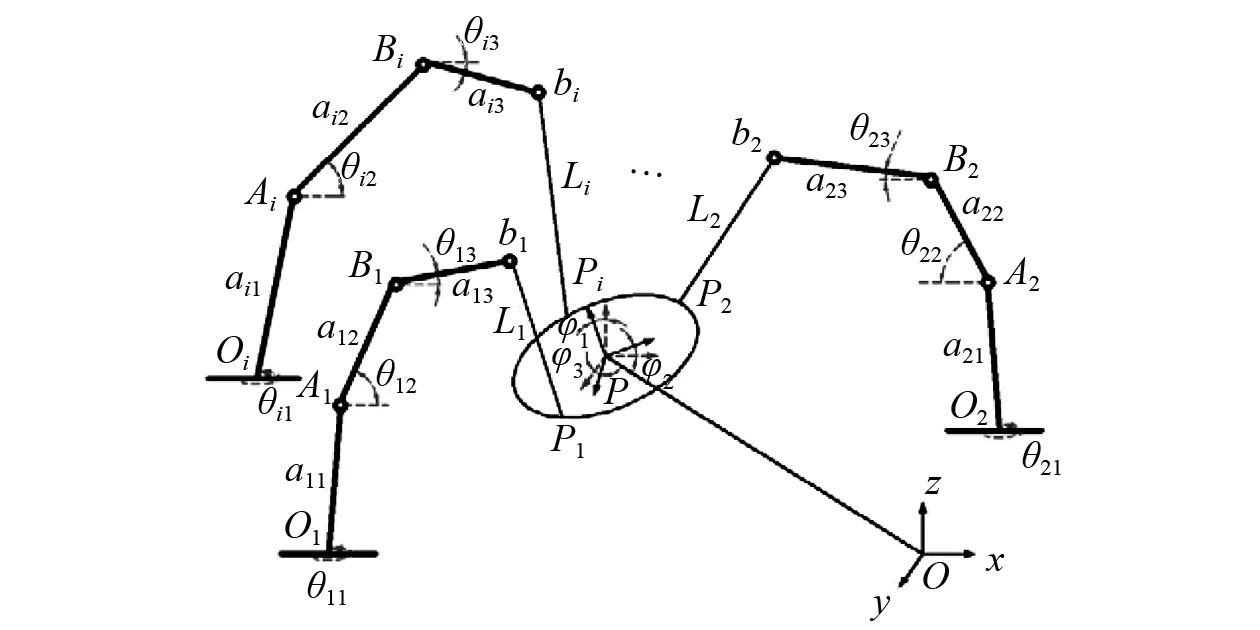
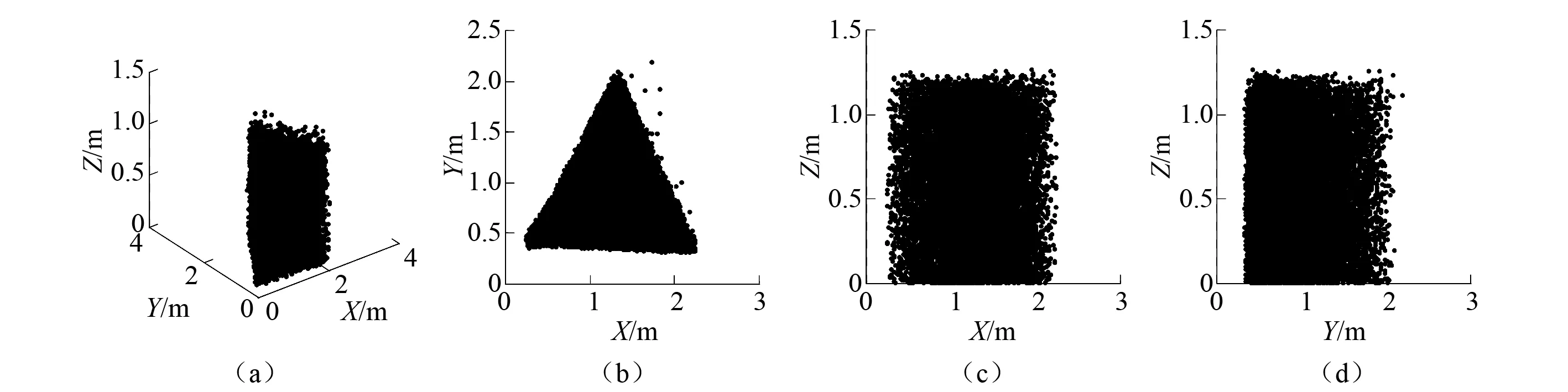
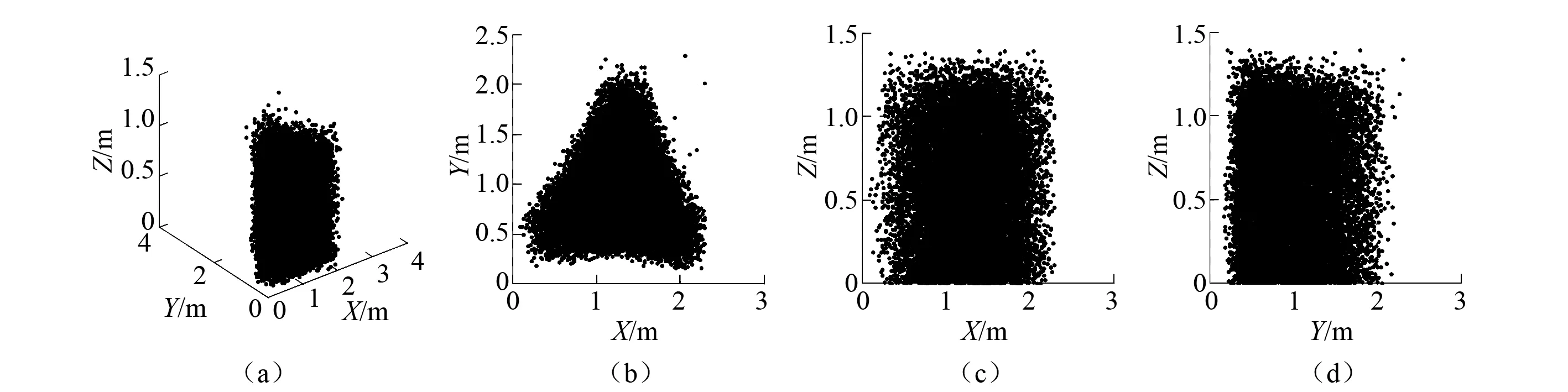
近年来,国内外对该类系统的相关研究形成了一定的体系,Ming等[5]根据柔索数目m和被吊运物的自由度数n之间的关系将柔索牵引并联机器人分为以下4 类: ①当m=n时, 为不完全约束定位机构(Incompletely Restrained Positioning Mechanisms,IRPMs);② 当m=1+n时, 为完全约束定位机构(Completely Restrained Positioning Mechanisms,CRPMs);③ 当m>1+n时,为冗余约束定位机构(Redundantly Restrained Positioning Mechanisms,RRPMs);④ 当m 由于柔索只提供单向拉力,吊运系统在运动过程中有摆动现象,该现象会影响系统的稳定性,因此研究系统稳定性可为系统的防摆控制提供一定的基础;而且现有文献主要针对m≥n的情况进行研究,对第4类欠约束吊运系统的研究很少。欠约束吊运系统具有结构简单、可操作度高以及系统可重组/拆卸程度高等优点,因此,本文主要针对欠约束吊运系统进行相关特性研究,首先根据系统的驱动配置情况将系统分为3类,并利用牛顿欧拉方程建立了系统的广义动力学建模,然后利用虚拟柔索发给出了欠约束系统力旋量封闭的解决方法,对吊运系统工作空间进行了分析,并根据广义逆矩阵理论给出了系统满足运动要求时柔索拉力的最优解,紧接着根据克拉索夫斯基法给出了系统的稳定性判据,同时给出了系统稳定程度评价指标,最后根据实例参数,分别对3类系统的工作空间进行了数值仿真,由于欠约束吊运系统的复杂性,无法用解析法判定系统的运动稳定性以及稳定程度,因此,应用方阵特征值分解法对工作空间内所有点的稳定性进行数值计算,结果为系统轨迹规划奠定了基础。 柔索式多机器人协调吊运系统是由模块化的串联机器人、柔索和被吊运物组成的并联机器人系统,对欠约束吊运系统而言,三者之间存在很强的力学耦合性。系统空间构型如图1所示。 被吊运物通过柔索悬挂在各机器人下方,其中:{O}为全局坐标系;{p} 为被吊运物体坐标系;bi为柔索与机器人末端的连接结点;Ai和Bi分别为各机器人第一、第二关节运动副;aij为第i台机器人的第j根连杆的有效长度;θij为各机器人的关节角位移;pi为柔索与被吊运物之间的连接结点;Li为柔索位置矢量,(φ1,φ2,φ3)为被吊运物的姿态;p(x,y,z)为被吊运物的位置。被吊运物空间位姿的变化可通过调节机器人末端位置和柔索长度来调整。柔索长度可由机器人末端的绕线轮来调节,机器人的数量和类型可根据实际任务的需求来确定。 图1 吊运系统空间构型Fig. 1 Spacial configuration of towing system 根据系统驱动配置情况将系统分为3类:① 定柔索长度,柔索长度确定,仅通过调节机器人末端位置来调整被吊运物的位姿;② 变柔索长度,固定机器人末端位置,通过调节柔索长度来调整被吊运物的位姿;③ 变柔索长度,变机器人末端位置,实现被吊运物位姿的变化。本文主要研究吊运系统的相关特性,单台机器人不在详细说明。 假设系统由m台机器人组成,实现被吊运物的n个自由度,且m (i=1, 2, …, m) (1) 式中:xi, yi, zi为各机器人末端bi在全局坐标系{O}中的位置;xpi, ypi,zpi为柔索与被吊运物连接点pi在全局坐标系{O}中的位置,且有 (2) 式中:[pxpi,pypi,pzpi]T为pi在体坐标系{P}中的位置;oRp为旋转矩阵。 oRp=Rz(φ3)Ry(φ2)Rx(φ1)= 被吊运物在m根柔索拉力的牵引和自身重力作用的下实现期望运动,由牛顿欧拉方程可得系统的广义动力学方程 AT=b (3) 式中,A为结构矩阵。 (4) T=[t1,t2,…,tm]T (5) (6) 3.1 力旋量封闭分析 由矢量封闭原理[17]知,在n自由度柔索并联系统中,至少需要n+1根柔索才能满足矢量封闭原理。而且矢量封闭原理可以保证每根柔索的拉力为正,且对任意的外力旋量都有解。 针对m根柔索6自由度欠约束吊运系统,为了满足力旋量封闭条件,可将被吊运物的重力和惯性力均视为不同虚拟柔索的拉力,其单位向量分别为eg,ex,ey,ez,这样系统动力学方程可表示为 J+T+=0 (7) 其中, (8) 式中:ax、ay、az分别为被吊运物在X、Y、Z轴方向上的平移加速度;Jw为重力和惯性力构成的旋量矩阵。 (9) 式中,Jg,Jx,Jy,Jz分别为被吊运物在重力方向、X、Y、Z轴方向上的旋量。 当柔索数目m=1,2时,通过各机器人协调运动和动态调整柔索长度,最多可以动态控制实现被吊运物n=3个自由度,考虑重力和各坐标轴方向上的旋量Jw时完全可以满足m≥n+1,即m=1,2时,有1≤n≤3,满足力旋量封闭条件;当柔索数目m≥3时,通过各机器人协调运动和动态调整柔索长度,最多可以动态控制实现被吊运物n=6个自由度,考虑旋量Jw时同样满足m≥n+1,即m≥3时,有1≤n≤6,满足力旋量封闭条件;对欠约束吊运系统而言,满足m≤n,因此,当m≥3时,3 依据多指无摩擦抓取模型以及凸集理论,可以得到m根柔索6自由度吊运系统判断力旋量封闭的凸条件: 条件1 吊运力旋量封闭; 条件2J+的列正张成Rn; 条件3 {Ji}的凸包包含原点的邻域; 条件4 不存在矢量η∈Rn,η≠0,满足所有的ηJi≥0,i=1,2,… ,m。 以上4个条件都是等价的,在应用中条件4在计算方面很有实际意义,矢量η可以由J+的列向量得到:通过任选J+的两个列向量构成支撑平面,用ηij表示其列向量Ji、Jj构成支撑平面的法向量。 3.2 工作空间分析与求解 并联机器人系统的工作空间分析求解方法主要有两种:解析法和数值法。虽然解析法可以很完整表述分析其工作空间,但该类并联机器人系统构型很复杂,存在力学耦合性,对欠约束并联机器人系统的位置解问题相关文献的研究至今没有完善的解决方法,所以,解析法不适用该类构型复杂的空间型并联机器人系统的工作空间求解,再加上要进一步考虑柔索拉力的可行变化范围,吊运系统的实际工作空间(即力旋量可行工作空间)会明显小于对应理论分析求解的工作空间,而且力旋量可行工作空间只能采用数值分析的方法来确定。尽管数值法具有计算量大和精度受限的缺陷,但数值法易于程序化、思路清晰,可以直观地显示吊运系统的实际工作空间,因此,本文将采用数值法求解吊运系统的工作空间,并在此基础上分析系统的稳定性。 系统的工作空间是指在满足系统约束条件时,系统执行器即被吊运物质心可到空间位置的集合,可以用数学描述为W={(x,y,z,φ1,φ2,φ3)∈R6|g0(x,y,z,φ1,φ2,φ3)≤0} (10) 式中:W为吊运系统的广义工作空间;x,y,z为被吊运物在全局坐标系中的位置坐标;φ1,φ2,φ3为被吊运物的姿态角;R6为六维实数域;g0为系统的约束条件式。 采用蒙特·卡洛方法随机产生机器人末端位置和被吊运物姿态,由式(1)、式(2)可以求得被吊运物的空间位置和柔索长度,被吊运物位置应满足 (11) 在给定被吊运物位姿时,方程式(3)可视为一个关于T的非齐次线性方程组,在不发生奇异运动时,rank(A)≤min(m,n),本文研究欠约束吊运系统,所以rank(A)≤m。如果rank(A) ≠rank(A,b),则方程组无解,即不满足系统约束条件;如果rank(A) =rank(A,b)=m,系统存在唯一解,此时,由式(3)可知柔索拉力为 T=A-1b (12) 如果rank(A) =rank(A,b) T*=AT(AAT)-1b (13) 其物理意义为满足被吊运物运动要求时柔索拉力的最优解。 柔索只能提供单向拉力,因此柔索拉力必须为正,且不能超过其柔索的最大允许拉力值,即柔索拉力应满足条件 (14) 式中:Tf max为柔索安全情况下的最大允许拉力;Tlim为柔索所能承受的极限拉力;k为安全系数,且1.5 具体计算步骤如下: 步骤1 采用蒙特·卡洛方法随机产生机器人末端位置和被吊运物姿态,通过式(4)、式(6)分别计算结构矩阵rank(A) 和rank(A,b); 步骤2 判断是否满足rank(A) =rank(A,b)=m,若是,则根据式(12)计算柔索拉力,进入步骤4,否则进入步骤3; 步骤3 判断是否满足rank(A) =rank(A,b) 步骤5 重复步骤1~步骤4直至结束。 系统稳定性是系统能正常工作的首要条件,是指系统受到外部干扰时,被吊运物是否能回到原有位姿状态的能力。本文根据克拉索夫斯基法给出系统稳定性判据,由于该系统的自身的复杂性,无法直接用解析的方法直接判定系统稳定性,因此,本文只在系统工作空间内应用数值方法进行系统稳定性判定,这样更具有工程应用价值。在计算时,应用方阵特征值分解法计算是否满足稳定性判据条件以及系统稳定程度评价指标。 结合式(1)和式(3),系统方程可表示为 f*(x)=0 (15) (16) 忽略高阶项Rn,整理后可进一步写为如下形式 (17) 该系统为非线性系统,因此应用克拉索夫斯基法判断系统稳定性。式(17)对x求偏导可写为 (18) 定义Lyapunov函数为 V(x)=fT(x)f(x) (19) 则有, f(x)[JT(x)+J(x)]fT(x)=f(x)F(x)fT(x) (20) F(x)=J(x)+JT(x) (21) 使F(x)矩阵负定,则表明系统渐进稳定。 若在上述函数中满足:当x→∞,有‖f(x)‖→∞时,进一步表明系统是大范围内渐进稳定,对该系统而言,这一点明显是成立的,故只需判定矩阵F(x)是否负定,即可判断系统是否稳定。 在计算系统稳定性时,应用方阵特征值分解的方法判断矩阵F(x)是否负定 F(x)V=VD (22) V=[v1,v2, …,vm] (23) (24) 式(22)可写成式(25)的形式,来求解特征值矩阵D (F(x)-DE)=0 (25) 式中:D为矩阵F(x)的特征值矩阵;矩阵V的列向量vi为矩阵F(x)的对应特征值λi的特征向量,由于F(x)是一个对称矩阵,所以其特征值都是实数。如果λi<0,则矩阵F(x)负定,系统运动稳定;否则,则矩阵F(x)非负定,系统运动不稳定。 为评价吊运系统在工作空间内运动的稳定程度,提出用工作空间内特征值λi的最大值S来衡量运动的稳定程度,即 S=max {λ1,λ2, …,λm} (26) 若S≥0,则系统不稳定或临界稳定;若S<0,则系统稳定,且S的值越小,系统运动稳定程度越高。 以3台机器人协调吊运同一重物为例,如图2所示为吊运系统中各机器人末端工作空间在XOY平面上的投影,在Z方向上各机器人末端可达位置范围为(1 m,1.4 m),假设被吊运物与柔索之间的连接结点成正三角形,且结点pi之间的距离l=0.1 m,被吊运物质量M=10 kg,转动惯量分别为Jx=0.54,Jy=0.26,Jz=0.28,ax=ay=az=0.000 1 m/s2,被吊运物姿态范围(-1 rad,1 rad), 柔索安全情况下的最大拉力Tf max=500 N,依据上面分析可知,被吊运物位置应在以机器人末端位置最大值及其投影所组成的三棱柱内。循环60 000次,对3类系统的工作空间进行数值仿真,进而对工作空间内运动稳定性进行计算。 图2 机器人末端工作空间在XOY平面上的投影Fig. 2 Projection of robot-ends workspace onto the XOY plane 5.1 工作空间 5.1.1 定柔索长度 定柔索长度是指仅通过调整各机器人末端位置来调节被吊运物的位姿,假设柔索长度Li=1.2 m,此时系统的工作空间如图3(a)所示,图3(b)、图3(c)及图3(d)分别给出了系统工作空间在XOY平面、XOZ平面和YOZ平面的投影。 图3 定柔索长度系统工作空间及投影Fig. 3 Workspace and projection for fixed cable length 综合图3(a)~图3(d)可知,定柔索长度时,系统的工作空间从下到上由类似倒立三角锥形变为类似长方体,共计33 871个可达位置点。X的取值范围X∈(1.15,1.34),Y的取值范围Y∈(0.7,1.18),Z的取值范围Z∈(0.6,1.38)。 为更加清楚表达其在不同高度的工作情况及性能,图4(a)、图4(b)、图4(c)及图4(d)分别给出了Z=0.6 m,Z=1.9 m,Z=1.2 m,Z=1.35 m时的工作截面,由图4(a)可知Z=0.6 m时的工作截面图类似三角形,图4(d)可知Z=1.35 m时的工作截面图类似长方形,结合图4(b),图4(c)和图4(d)可知越往上,截面形状越类似于长方形。其主要原因有:其一是柔索长度的固定,其二是各机器人末端工作空间为长方体的缘故。 图4 不同高度下的工作截面Fig. 4 Work cross sections in different high 5.1.2 变柔索长度 变柔索长度是指固定各机器人末端,仅通过调整柔索长度来实现被吊运物期望位姿的变化。将各机器人末端固定在其工作空间的几何中心,即各机器人末端位置坐标为b1(2.2,0.45,1.2),b2(1.275,2.027,1.2),b3(0.308,0.405,1.2),变柔索长度时,系统工作空间如图5(a)所示,图5(b)、图5(c)及图5(d)分别给出了系统工作空间在XOY平面、XOZ平面和YOZ平面的投影。 图5 变柔索长度系统工作空间及投影Fig. 5 Workspace and projection for variable cable length 综合图5(b)~图5(d)可知,变柔索长度时,系统的工作空间为以三台机器人末端及末端的投影点组成的三棱柱,共计16 189个可达位置点。X的取值范围X∈(0.31,2.2),Y的取值范围Y∈(0.45,2),Z的取值范围Z∈(0,1.18)。 5.1.3 柔索长度和机器人末端同时变 机器人末端和柔索长度同时变化来实现被吊运物期望位姿的变化,在此情况下系统的工作空间如图6(a)所示,图6(b)、图6(c)及图6(d)分别给出了系统工作空间在XOY平面、XOZ平面和YOZ平面的投影。 图6 柔索长度和机器人末端同时变化时系统工作空间及投影Fig. 6 Workspace and projection for variable cable length and robot-ends’ position 综合图6(b)~图6(d)可知,柔索长度和机器人末端位置同时变化时,系统的工作空间也为以三台机器人末端及末端的投影点组成的三棱柱,但范围要比变柔索长度大,共计16 275个可达位置点。X的取值范围X∈(0.15,2.3),Y的取值范围Y∈(0.2,2.2),Z的取值范围Z∈(0,1.38)。 综上所述,三类系统的工作空间依次增大,定柔索长度系统工作空间体积最小,变柔索长度系统工作空间的体积次之,柔索长度和机器人末端位置同时变化时系统工作空间体积最大,并且依次存在包含关系。 5.2 运动稳定性仿真分析 表1分别给出了三类系统在工作空间内所有点F(x)特征值分解情况,由表1可知所有点均满足特征值λi<0,矩阵F(x)负定,即三类系统在各自工作空间内运动均是稳定的。由三类系统S值的大小可知,定柔索长度情况下系统稳定性最好,变柔索长度情况的稳定性次之,最后是柔索长度和机器人末端位置同时变化的情况,为后续吊运系统轨迹规划和系统防摆控制提供了依据。 表1 3类系统F(x)特征值分解情况 对欠约束多机器人协调吊运系统的工作空间和运动稳定性进行分析。首先依据系统驱动配置情况的不同,将吊运系统分成3类系统;然后应用牛顿欧拉方程建立了系统的广义动力学模型,针对欠约束吊运系统,采用虚拟柔索法给出了实现力旋量封闭的处理方法,对系统的工作空间进行分析,并根据广义逆矩阵理论给出了满足运动要求时柔索拉力的最优解;随后利用克拉索夫斯基法给出了系统运动稳定性判据;最后结合实例,对3类系统的工作空间进行了数值仿真分析,并给出了3类系统工作空间体积大小和包含关系;应用方阵特征值分解法计算各工作空间内所有点的运动稳定性,结果表明,3类系统在各自工作空间内运动是稳定的,并获得了3类系统的稳定程度关系,研究结果为进一步优化吊运系统的轨迹规划和防摆控制奠定了基础。 [ 1 ] AGHELI M, NESTINGER S S. Closed-form solution for reachable workspace of axially symmetric hexapod robots[C]∥ The 8th IEEE/ASME International Conference on Mechatronics and Embedded Systems and Applications. [S.l.]: IEEE, 2012: 75-79. [ 2 ] 赵志刚,吕恬生.多机器人协同吊运系统的协调动态载荷分配[J].机器人,2012,34(1):114-119. ZHAO Zhigang, LÜ Tiansheng. Cooperative dynamic load distribution for Multi-robot coordinative towing system[J]. Robot, 2012, 34(1): 114-119. [ 3 ] 王砚麟,赵志刚,石广田. 多机器人协调吊运系统控制优化仿真[J]. 计算机仿真,2015,32(10):404-408. WANG Yanlin, ZHAO Zhigang, SHI Guangtian. Control optimal simulation of multi-robot cooperatively towing system[J]. Computer Simulation, 2015, 32(10):404-408. [ 4 ] 李巍,赵志刚,石广田,等.多机器人并联绳牵引系统的运动学及动力学解[J]. 浙江大学学报(工学版), 2015, 49(10): 1916-1923. LI Wei, ZHAO Zhigang, SHI Guangtian, et al. Solutions of kinematics and dynamics for parallel cable-driven system with multi-ronot[J]. Journal of Zhejiang University (Engineering Science), 2015, 49(10): 1916-1923. [ 5 ] MING A,HIGUCHI T. Study on multiple degree of freedom positioning mechanisms using wires, Part 1: concept,design and control[J]. International Journal of the Japan Society for Precision Engineering, 1994, 28(2) : 131-138. [ 6 ] ZI Bin, QIAN Sen, DING Huafeng, et al. Design and analysis of cooperative cable parallel manipulators for multiple mobile cranes[J]. International Journal of Advanced Robotic Systems, 2012, 9: 56-61. [ 7 ] ZI Bin, DING Huafeng, WU Xia, et al. Error modeling and sensitivity analysis of a hybrid-driven based cable parallel manipulator[J]. Precision Engineering, 2014,38(1):197-211. [ 8 ] ZI Bin, ZHU Zhencai, DU Jingli. Analysis and control of the cable-supporting system including actuator dynamics[J]. Control Engineering Practice, 2011, 19(5): 491-501. [ 9 ] ZI Bin, LIN Jun, QIAN Sen. Localization, obstacle avoidance planning and control of a cooperative cable parallel robot for multiple mobile cranes[J]. Robotics and Computer-Integrated Manufacturing, 2015, 34(9): 105-123. [10] 赵志刚,腾富军,石广田,等.紧耦合多机器人联合吊运系统逆运动学求解[J]. 哈尔滨工程大学学报,2016,37(2): 1-7. ZHAO Zhigang, TENG Fujun, SHI Guangtian, et al. The inverse kinematics analysis of multi-robot combined lifting system[J]. Journal of Harbin Engineering University,2016,37(2):1-7. [11] ZHOU Xiaobo, JUN S K, KROVI V. Tension distribution shaping via recongurable attachment in planar mobile cable robots[J]. Robotica, 2014, 32(10): 245-256. [12] ALBERTO T. Planning of dynami cally feasible trajectories for translational, planar, and undercon-strained cable-driven robots[J]. Journal of Systems Science & Complexity, 2013, 26(10):695-717. [13] 赵志刚,腾富军,石广田,等. 多机器人联合吊运系统可行域分析与求解[J].上海交通大学学报, 2015,49(8): 1174-1180. ZHAO Zhigang, TENG Fujun, SHI Guangtian, et al. Analysis and calculation on the feasible region of multi-robot combined lifting system[J]. Shanghai Jiao Tong University, 2015,49(8): 1174-1180. [14] MICHAEL N, FINK J, KUMAR V. Cooperative manipulation and transportation with aerial robots [J]. Autonomous Robot, 2011, 30(1): 73-86. [15] BOSSCHER P, EBERT I. A stability measure for underconstrained cable-driven robots[C]∥ In Proceedings of 2004 IEEE International Conference on Robotics & Automation. New Orleans: IEEE, 2004. [16] 赵志刚,吕恬生.多无人直升机吊运系统运动学与稳定性的仿真[J].系统仿真学报, 2013,25(4): 791-794. ZHAO Zhigang, LÜ Tiansheng. Simulation on kinematics and stability of multi-helicopters hoist system[J]. Journal of System Simulation, 2013, 25(4): 791-794. [17] 梁永红. 冗余绳牵引并联机器人工作空间求解方法及性能的研究[D]. 西安:西安电子科技大学, 2010. Analysis of the workspace and dynamic stability of a multi-robot collaboratively towing system WANG Yanlin1, ZHAO Zhigang1, SU Cheng1, LI Jinsong2, JI Gang2 (1. School of Mechatronic Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China;2. School of Mechatronical and Power Engineering, Shanghai Jiao Tong University, Shanghai 200030, China) This paper aims to analyze the workspace and dynamic stability of a multi-robot collaboratively towing system. Firstly, the towing system was divided into three types of systems according to the driving configuration. Secondly, a generalized dynamic model of the system was established by Newton-Euler equations. Next, the method to solve the wrench enclosed of an under-constrained system was given by using the method of virtual cables. Its workspace was analyzed. An optimal result of the cables tension that satisfies the motion requirements of the system was given based on the generalized inverse matrix theory. Subsequently, the criterion of dynamic stability was given by the Krasovskii method. Finally, the system was parameterized by combining with a practical example. Numerical simulation and analysis of the workspaces of three types of systems were given. Stability calculations of all workspace's spots were done by using the method of the square matrix eigenvalue decomposition. The results show that three types of systems were dynamically stable in their workspaces. The relationships for the degree of stable of the three kinds of systems were obtained. The results have provided foundation for further research on optimization of motion trajectory planning and anti-sway control of towing systems. towing system; multi-robots system; generalized dynamic model; workspace; stability analysis 国家自然科学基金资助(51265021);高等学校博士学科点专项科研基金新教师类资助课题(20126204120004);教育部科学技术研究重点(212184);甘肃省自然科学基金资助(1212RJZA067) 2016-03-29 修改稿收到日期: 2016-07-08 王砚麟 男, 硕士, 1992年生 赵志刚 男, 博士, 教授, 1975年生 N945.12; TP391. 9 A 10.13465/j.cnki.jvs.2017.16.0071 系统构型及分类
2 系统动力学建模
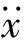
3 工作空间分析
4 稳定性分析
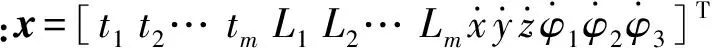
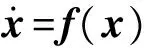
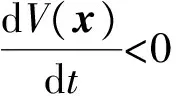
5 数值仿真分析
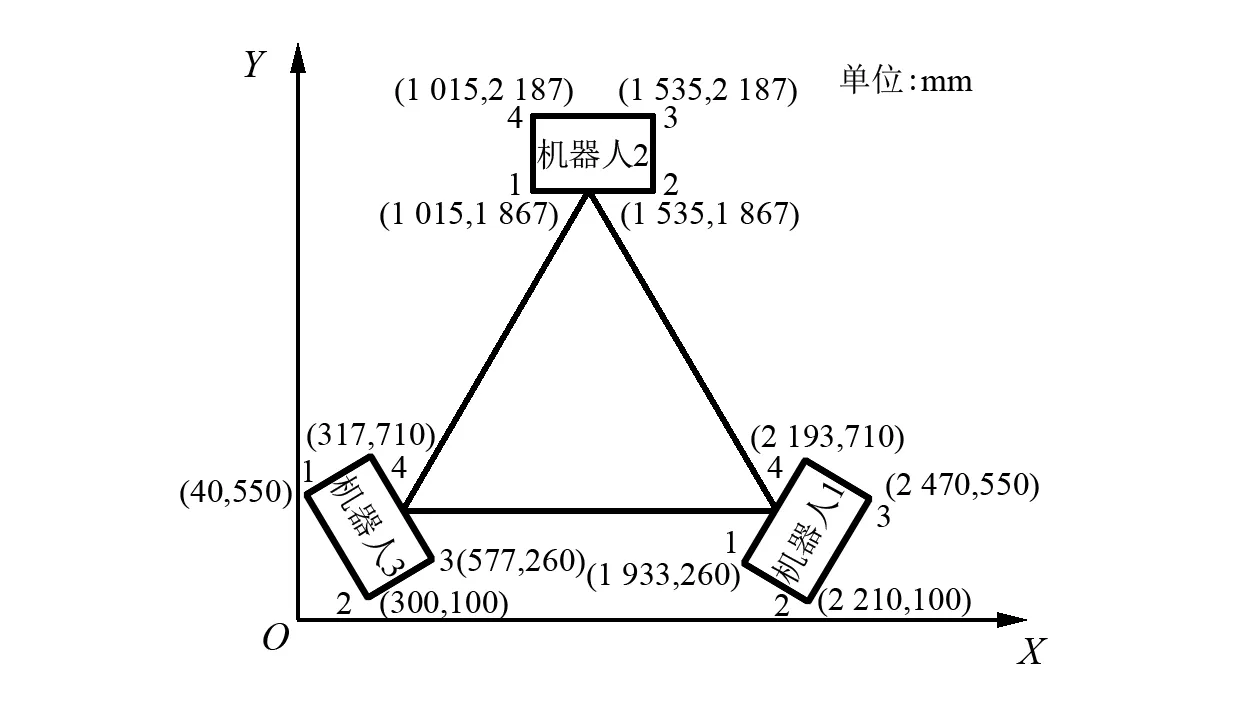
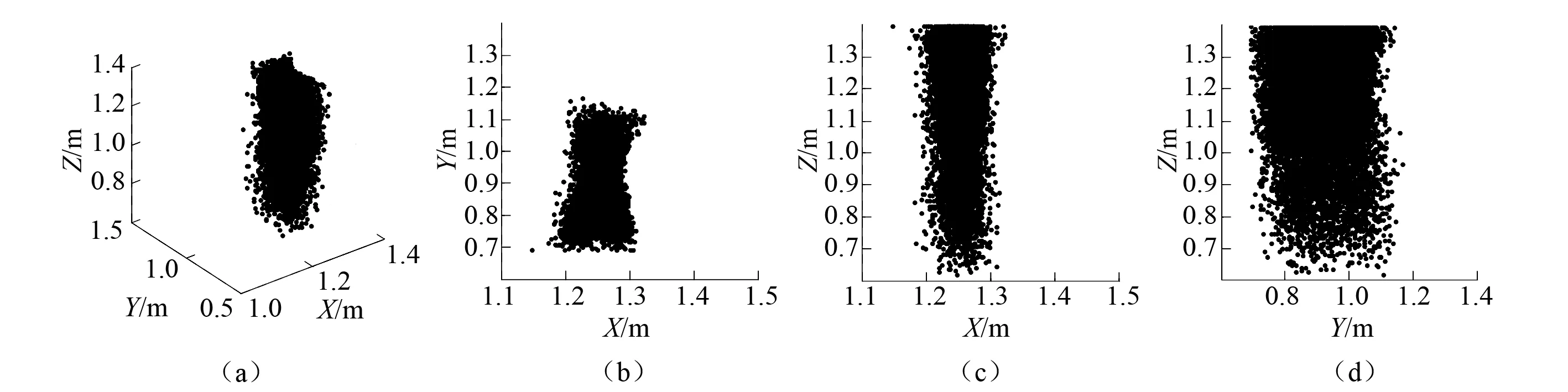
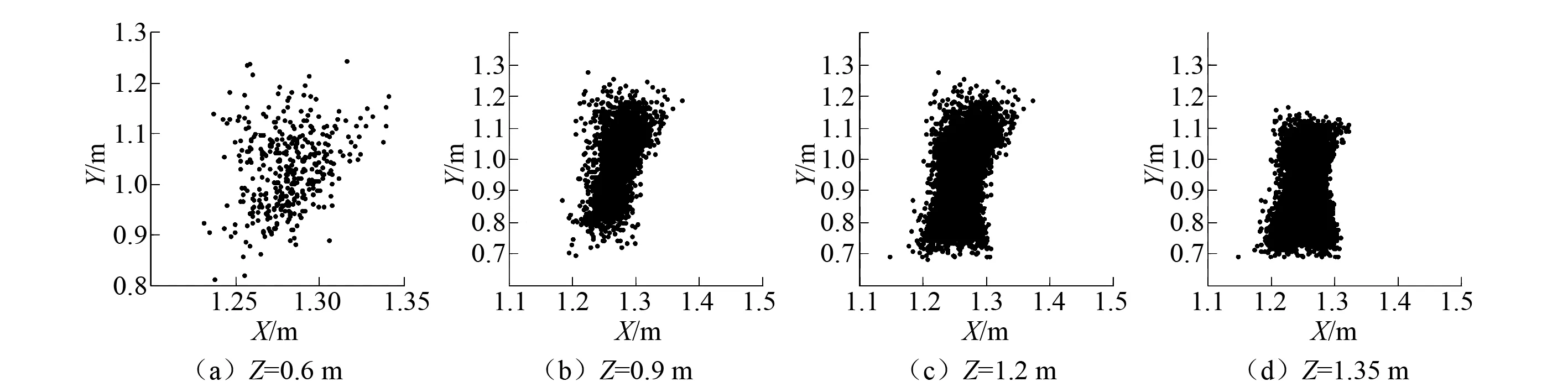

6 结 论
