基于Hertz理论的泥石流块石冲击力修正系数研究

陈 剑， 王全才， 王 浩， 陈颖骐， 李 俊

(1.中国科学院 山地灾害与地表过程重点实验室，成都 610041；2.中国科学院 水利部成都山地灾害与环境研究所，成都 610041；3.中国科学院大学，北京 100049；4.河南大学 土木建筑学院，河南 开封 475001)

基于Hertz理论的泥石流块石冲击力修正系数研究

陈 剑1,2,3， 王全才1,2， 王 浩4， 陈颖骐1,2,3， 李 俊1,2,3

(1.中国科学院 山地灾害与地表过程重点实验室，成都 610041；2.中国科学院 水利部成都山地灾害与环境研究所，成都 610041；3.中国科学院大学，北京 100049；4.河南大学 土木建筑学院，河南 开封 475001)

基于Hertz弹性碰撞理论的修正公式是计算泥石流块石冲击力的有效方法之一，但公式中的修正系数目前尚无具体的量化方法。在Hertz接触理论和Thornton弹塑性假设的基础上，建立了泥石流块石冲击构筑物的计算模型，推导了修正系数的表达式。研究表明，修正系数是材料强度、泥石流块石尺寸和速度的函数而非一个常量，其随泥石流块石冲击速度的增加而减小，随泥石流块石半径、构筑物材料强度的增加而增加。板子沟泥石流沟防治工程计算结果显示，修正冲击力仅为Hertz弹性碰撞冲击力的15.58%。当泥石流块石冲击速度小于 3 m/s，修正系数大于0.20；当泥石流块石冲击速度大于3 m/s，修正系数介于0.10～0.20，计算结果与实践估计较为一致。

泥石流；块石冲击力；修正系数；Hertz接触力学；Thornton弹塑性假设

泥石流是山区常见的地质灾害之一，在泥石流灾害频繁发生的地区，对其危害范围内的各种构筑物造成了严重威胁[1-2]。泥石流对构筑物的危害方式主要表现为冲击和淤埋[3]，尤以块石冲击破坏最为显著[4-5]。如1981年7月9日，成昆铁路利子依达沟发生的特大泥石流携带数米的大块石，其强大冲击力冲毁桥墩，使正在行驶的一列火车跌入泥石流，造成360多人死亡[6]；1991年7月26日爆发的索通沟泥石流，其携带的大块石将东侧桥墩拱脚击毁，造成混凝土双曲拱桥完全被破坏[7]。类似由泥石流大块石冲击而引起的灾害案例引起了各国学者的重视，有关泥石流大块石的冲击力计算成为泥石流研究的热点[8-9]。

目前泥石流块石冲击力计算有多种方法。如章书成等[10]以材料力学和结构力学为基础，将构筑物简化为悬臂梁、简支梁模型来计算泥石流大块石作用于梳子坝支墩、桥梁等柱型结构上的冲击力。工程实践表明，此法计算结果比估计的承载力大[11]。Thornton[12]将泥石流大块石与被冲击物分别简化为刚性体和塑性体来推导出泥石流的冲击力公式，其适用于强度较低或年代久远的构筑物被冲击的情况。工程应用表明，此法得出的冲击力远小于其他计算方法所得的冲击力。何思明等[13-14]以Hertz弹性碰撞理论为基础，考虑不同因素如结构刚度、构筑物材料强度对冲击力的影响从而推导了相应的冲击力计算公式。Yamaguchi等[15-17]将泥石流中大块石与结构的碰撞视为两个球的对心碰撞，并采用修正系数的方法来考虑冲击过程中接触面的断裂、摩擦、微小凸凹及流体的缓冲压力对冲击力的综合影响。这种基于Hertz理论进行修正的方法是目前国内外计算泥石流大块石冲击力的主流方法之一。但其最大的不足是修正系数力学意义模糊，一般通过工程经验或实验确定，具有主观性强，成本高昂或耗时周期长等缺点[18]。

本文以Hertz弹性碰撞理论为基础，在Thornton弹塑性假设的条件下推导了泥石流大块石冲击力的计算公式，并对泥石流块石冲击力修正系数进行了量化，弥补了经验法确定修正系数的不足，其理论依据充分，参数明确，使用方便，可为泥石流多发区的防护结构设计提供可信的计算方法。

1 冲击力的修正表达

Hertz在假设两球体接触面半径为a的圆的前提下，给出了两个球体在压力作用P下的完备解，并给出了碰撞时的冲击力式(1)～式(3)[19-20]，如图1所示。

图1 Hertz弹性碰撞模型Fig.1 Elastic collision model of Hertz

接触面压应力分布公式

(1)

式中：P(r)为接触压应力；P为接触压力；a为接触面半径；r为接触半径变量，取值范围为0～a。

接触变形量与接触面半径之间有如下关系

(2)

式中：R为等效半径，R1、R2分别为两个碰撞球体的半径；δ为总压缩量，δ1、δ2分别为两个碰撞球体的变形量。

两球碰撞时的冲击力公式

(3)

式中：E为等效模量，E1、E2分别为两个碰撞球体的弹性模量；μ1、μ2分别为两个碰撞球体的泊松比。

国内外学者在Hertz弹性碰撞理论的基础上，将大块石与构筑物的碰撞视为弹性碰撞，采用修正系数k来考虑材料、摩擦和断裂耗能等对实际冲击力的影响，提出了计算泥石流块石冲击力的通用式(4)

(4)

式中：F为修正冲击压力；k为修正系数。

目前，对修正系数k的确定主要通过经验估计或试验为主，相关的理论计算还未见报道。如Mizuyama根据烧岳山的测量数据估计k=0.2，Yamaguchi根据MyoukouPlateau治理工程实践得出k=0.1，周必凡等[21]对泥石流大块石冲击力进行了计算，并与实测值对比得出k = 0.06～0.11。可以看出，上述修正系数取值离散，主观性强，因此有必要对修正系数进行量化。

2 Thornton弹塑性假设

材料相互接触时，当最大接触压应力超过材料屈服强度时，就会在接触面上产生塑性变形区。采用Thornton假设，忽略材料的塑性硬化或塑性软化特性，视碰撞系统材料为理想弹塑性材料，材料屈服后，塑性区内的接触压应力为一常数[22]，如图2所示。

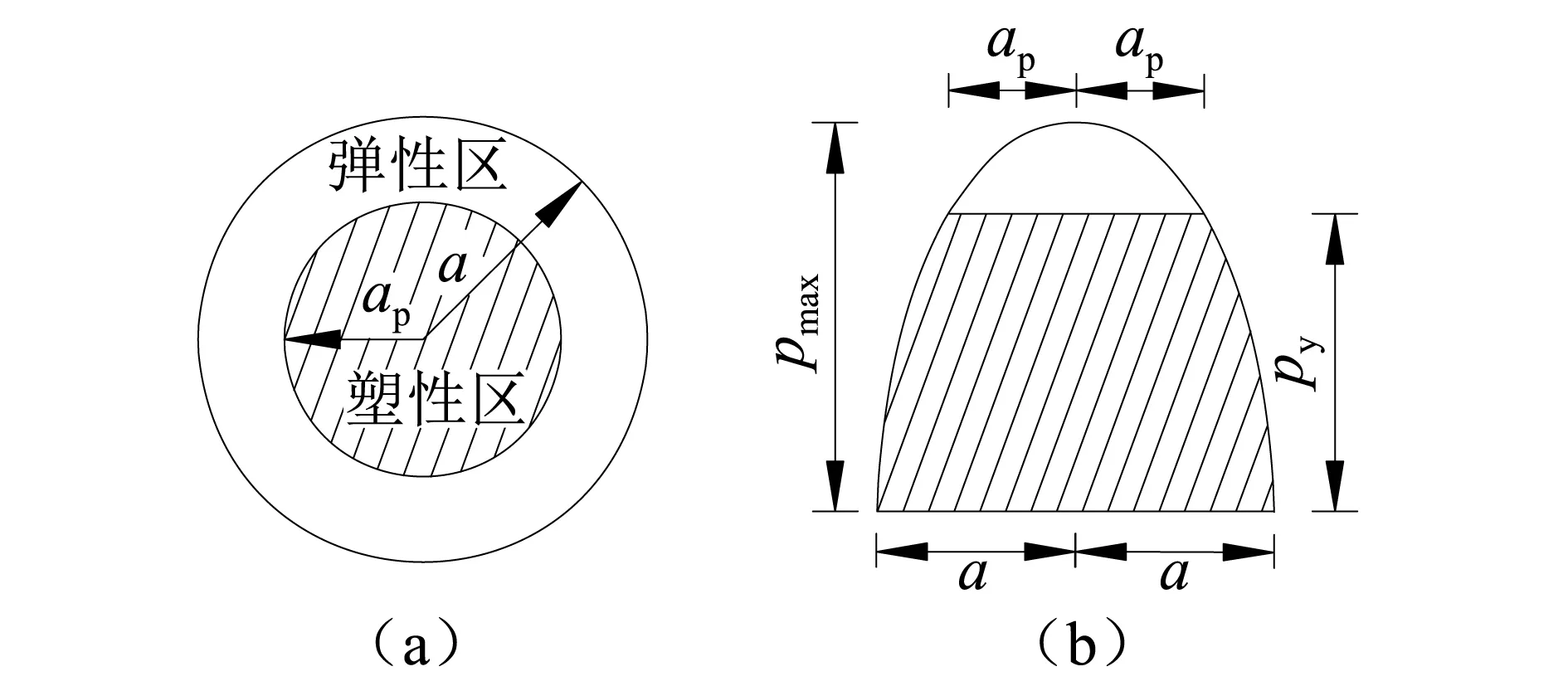
图2 理想弹塑性材料压应力分布Fig.2 Distribution of contact compressive stress of ideal elastoplastic material

由式(1)～式(3)可求出屈服压应力与初始屈服对应的接触半径之间的关系式(5)

(5)

式中：py为接触屈服压应力；ay为初始屈服对应的接触面半径。

假设在某荷载P作用下，半径为ap范围内的接触面产生屈服，而超过这一范围的接触面仍满足Hertz应力分布。根据式(1)有

(6)

结合式(2)、式(3)和式(5)可得到式(7)

(7)

则两个物体之间的接触压力如式(8)所示

(8)

3 修正系数的量化

3.1 冲击力的弹性解

根据Hertz弹性碰撞理论，质量为m1、运动速度为v1的球体对心碰撞于质量为m2、运动速度为v2的球体，当冲击球体的半径远小于被冲击球体的半径，即r2≫ r1，v2=0时，可将冲击球体视为泥石流大块石，被冲击球体视为在坝体自重和坝肩岩土体抗力作用下能保证坝体倾覆和滑移稳定性的静止构筑物，从而建立泥石流块石对静止拦挡坝的冲击模型，如图3所示。

图3 泥石流块石对拦挡坝的冲击模型Fig.3 Impact model between boulder and blockingdam

根据牛顿第二定律有

(9)

由式(9)变形得式(10)

(10)

由式(3)可得冲击压力与接触变形的关系式(11)

(11)

式中，m为等效质量，m1、m2分别为两碰撞球体的质量。

对变形压缩量进行积分并考虑作用点位置，则碰撞过程中最大压缩量δ如式(12)所示

(12)

结合式(3)和式(12)，得出弹性冲击力式(13)

(13)

式中，Pe为弹性冲击力。

3.2 冲击力的弹塑性解

冲击过程中，当冲击速度较小时，在物体冲击接触面上为弹性接触，可直接用式(13)求得冲击力。当冲击速度大至一定量时，必然在冲击接触面上产生塑性变形区，此时存在一个临界冲击速度vc，由式(1)、式(3)、式(6)和式(12)可得关系式(14)

(14)

则临界冲击速度为式(15)

(15)

式中，ρ为块石的天然密度。

Vu-Quoc[23-24]以Hertz接触理论为基础，在假设构筑物材料满足vonMises屈服准则的条件下，推导了接触屈服压应力与材料强度之间的定量关系

(16)

式中：μ为冲击物的泊松比；η(μ)为μ的函数，η(0.3)=

1.613，η(0.4)=1.738，当μ为其它值时，作线性插值处理；σy为被冲击物的屈服强度，对于脆性材料取0.2%残余变形对应的应力值。

工程实践中，当冲击速度小于临界冲击速度时，块石冲击力按式(13)计算；当冲击速度大于临界冲击速度时，在接触面上必然会产生塑性区，此时应考虑塑性区扩展对冲击力大小的影响，结合式(1)、式(7)、式(12)、式(16)，得出块石的弹塑性冲击压力式(17)

(17)

式中，Pep为弹塑性冲击压力。

3.3 冲击力修正系数

(18)

由式(18)可以看出，修正系数k与ay、ap和a的大小相关。其中，ay由冲击系统材料和大小决定，其值可通过式(5)和式(16)求出；a由冲击系统的材料、大小及块石速度确定，其值可通过式(2)和式(12)求出；ap值可通过式(7)求出。可以看出，冲击力修正系数不仅与材料性质、冲击系统对象尺寸有关，其还随块石冲击速度的变化而变化。将式(18)的表达式代入式(4)，即可得到修正冲击力公式。

4 实例研究与分析

为验证本文方法的合理性，以板子沟拦挡坝受泥石流大块石冲击为例予以说明。

该处拦挡坝材料为C35混凝土，密度2 420kg/m3；大块石为花岗岩，密度2 700kg/m3，等效半径R=0.8m。根据板子沟泥石流现场雷达测速仪所获取的观测数据，同时结合其洪痕断面和改进曼宁公式的计算结果进行校验，最终取观测数据中的最大值v=5.6m/s作为泥石流大块石速度来研究泥石流大块石对拦挡坝的冲击力，相关计算参数见表1。

表1 泥石流中块石冲击力计算参数

计算结果表明，泥石流大块石的临界冲击速度仅为0.02 m/s，现实中泥石流流速一般远高于此值，在本例研究中，泥石流块石以5.6 m/s的速度冲击下势必形成大范围的塑性区。如直接使用Hertz碰撞理论求得的弹性冲击压力P=22 581.27 kN，采用如此高的冲击力进行泥石流防治工程设计，势必会造成很大的浪费。采用本文的计算方法所计算出的修正冲击压力F=3 518.45 kN，修正冲击压力仅为弹性冲击压力的15.58%。黄宏斌等采用日本KYOWA公司生产的冲击力测量系统进行泥石流块石对拦挡坝的冲击进行模型试验，结果表明试验值与Hertz理论值之比约为5.3%～7.6%。Mizuyama采用圆锥下沉的方法测定了日本烧岳山泥石流块石的冲击力，其现场试验值与Hertz理论值之比高达11%，考虑到安全问题，Mizuyama指出实际冲击力宜取Hertz理论值的20%。可以看出，本文方法的计算结果略大于模型或现场试验结果，具有一定的安全储备；同时小于Mizuyama经验估值，具有一定的经济性，综合表明了本文计算方法的合理性和可靠性。

从图4、图5可以看出，随块石冲击速度的增大，弹性冲击压力急剧增加，而修正冲击压力增长相对缓慢。随速度增加，接触面上的塑性区先急剧增大而后平稳增长，相应的冲击力修正系数先急剧降低而后缓慢降低，说明了实际冲击力的增幅受到了塑性区发展的限制。从图5可以看出，泥石流块石冲击过程中塑性区半径较小，相应的塑性区压缩量也较低，因此可在构筑物如泥石流拦挡坝表面施工一定厚度的低强度的混凝土，以减少块石对构筑物施加的冲击力，并在破坏后进行修复以预防下一次泥石流块石的冲击。

图4 不同冲击压力与块石速度的关系Fig.4 Relation between impact force and boulder velocity

图5 修正系数与塑性区半径和块石速度的关系Fig.5 Relation between modified coefficient, radius of plastic zone and boulder velocity

图6、图7显示了不同修正方法随块石速度变化时相应冲击力的变化情况，计算结果表明当v<3 m/s时，本文修正方法所求得的冲击力均大于Yamuguchi等[15-16]修正方法所求得的冲击力，即k≥0.2；当v>3 m/s时，本文修正方法求得的冲击力介于Yamuguchi等修正方法所求得的冲击力之间，即0.2≥k≥0.1。随速度增加，本文修正方法所求得的冲击力逐渐趋近于Yamuguchi修正方法所求得的冲击力，背离Mizuyama修正方法所求得的冲击力。主要原因在于本文提出的修正系数是一个与速度有关的变量，可以反映不同速度下冲击力的动态响应，而Yamuguchi等修正方法所提出的修正系数仅是根据经验而定的两个离散常量。

图8表明，修正系数随材料强度的增加而增大，随速度增加而降低。高强度和高弹性模量的材料在块石低速冲击的情况下显示更强的弹性性质，修正系数随速度增加先急剧衰减，而后逐渐趋于平缓。低强度和低弹性模量的材料表现出更强的弹塑性性质，随速度增加修正系数变化相对平稳，修正系数总体上表现为一个较平稳的低值，这说明了强度和弹性模量较低的混凝土构筑物能有效降低作用在构筑物上的块石冲击力。

图6 不同修正方法计算冲击力比较Fig.6 Comparison of impact force caculatedby different methods

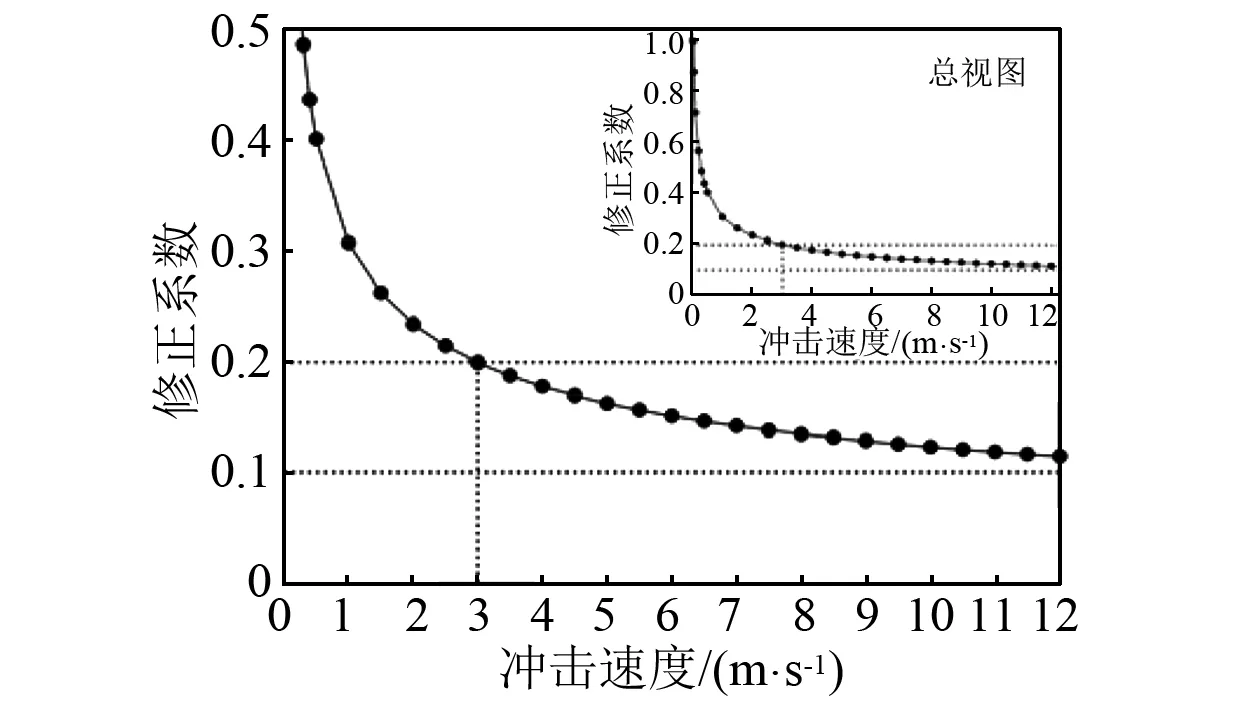
图7 修正系数与块石冲击速度关系Fig.7 Relation between modified coefficientand boulder velocity

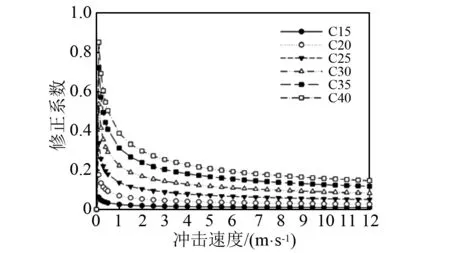
图8 修正系数与构筑物材料和块石速度的关系Fig.8 Relation between modified coefficient and bouldervelocity (different materials)

图9表明，随块石半径增加，修正系数显著增长，临界冲击速度增大。当块石半径较小，修正系数较小，且总体较为平缓。随块石半径增加，修正系数也逐渐增加，且在块石低速冲击的情况下修正系数随块石半径的增加而增长速率较大。与构筑材料对修正系数的影响相比，块石半径对修正系数的影响更为显著。当块石半径R>1.0 m时，修正系数将显著增长，因此在工程设计前应对泥石流沟展开详细的野外调查工作以确定最大块石的等效半径。

图9 修正系数与块石半径和速度的关系Fig.9 Relation between modified coefficient and bouldervelocity (different boulder radius)

5 结 论

基于Hertz接触理论和Thornton弹塑性假设，建立了泥石流块石冲击构筑物的计算模型，导出了泥石流大块石对构筑物的修正冲击力表达式。以板子沟泥石流沟块石对拦挡坝的冲击进行实例研究，得出以下结论：

(1)冲击力修正系数是块石冲击速度、冲击系统材料性质和块石尺寸的函数而非一个常量。其随块石冲击速度的增加而降低，随构筑物材料强度和弹性模量、块石半径的增加而增加。

(2)混凝土为典型的弹塑性材料，块石以很小的速度冲击混凝土结构即可产生塑性区。直接采用Hertz理论计算的泥石流块石冲击力偏大，考虑了拦挡坝材料的弹塑性质所计算出的冲击力更为接近实际情况。

(3)直接采用Hertz理论计算的冲击力随块石冲击速度的增加而急剧增长，考虑材料弹塑性质所计算出的冲击力随块石冲击速度增加而缓慢增加，实际冲击力的增幅受到塑性区发展的限制。

(4)直径为0.8 m的块石冲击C35混凝土结构时，当v<3 m/s时，k>0.2，以弹性冲击为主；当v≥3 m/s时，0.2≥k≥0.1，以弹塑性冲击为主。修正系数与工程实践估计具有良好的一致性，证明了修正系数表达式的合理性。

(5)泥石流防治工程设计前，应充分调查工程区内泥石流块石半径分布情况，以便较准确估算泥石流块石对结构的冲击力。设计中，可在防治工程结构表面施作一定厚度的低强度混凝土以降低块石对结构的冲击力，增强其抗冲击性能。

[ 1 ] ZENG Chao, CUI Peng, SU Zhiman, et al. Failure modes of reinforced concrete columns of buildings under debris flow impact[J]. Landslides, 2015, 12(3): 561-571.

[ 2 ] 程选生,张爱军,任毅,等. 泥石流作用下砌体结构的破坏机理和防倒塌措施[J]. 工程力学,2015,32(8):156-163. CHENG Xuansheng, ZHANG Aijun, REN Yi,et al.Failure mechanism and anti-collapse measures ofmasonry structure under debris flow[J]. Engineering Mechanics, 2015, 32(8):156-163.

[ 3 ] CHENG Xuansheng, WANG Junling, REN Yi. Fluid-solid interaction dynamic response of masonry structures under debris flow action[J]. European Journal of Environmental & Civil Engineering, 2013, 17(9):841-859.

[ 4 ] HE Siming, LIU Wei, LI Xinpo. Prediction of impact force of debris flows based on distribution and size of particles[J]. Environmental Earth Sciencess, 2016, 75(4): 1-8.

[ 5 ] 于献彬, 陈晓清, 李昆, 等. 复合型拦砂坝受泥石流大块石冲击作用的动力响应[J].施工技术, 2015,44(24): 114-119. YU Xianbin, CHEN Xiaoqing, LI Kun, et al. Compound dam dynamic response to the impact ofmassive stone in debris flow[J]. Construction Technology, 2015, 44(24): 114-119.

[ 6 ] 胡凯衡, 韦方强, 洪勇, 等. 泥石流冲击力的野外测量[J].岩石力学与工程学报, 2006,25(增刊1): 2813-2819. HU Kaiheng, WEI Fangqiang, HONG Yong. Field measurement of impact force of debris flow[J]. Chinese Journal of Rock Mechanics and Engineering, 2006,25(Sup1): 2813-2819.

[ 7 ] 钟敦伦, 谢洪. 泥石流灾害及防治技术[M]. 成都：四川科学技术出版社, 2014.

[ 8 ] 王强, 何思明, 张俊云. 泥石流防撞墩冲击力理论计算方法[J]. 防灾减灾工程学报, 2009, 29(4): 423-427. WANG Qiang, HE Siming, ZHANG Junyun. Theoretical method for calculating impact force on debris flow protection piers[J]. Journal of Disaster Prevention and Mitigation Engineering, 2009, 29 (4): 423-427.

[ 9 ] 何思明, 吴永, 沈均. 泥石流大块石冲击力的简化计算[J]. 自然灾害学报, 2009, 18(5): 51-56. HE Siming, WU Yong, SHEN Jun. Simplified calculation of impact force of massive stone in debris flow[J]. Journal of Natural Disasters, 2009, 18(5): 51-56.

[10] 章书成, HUNGR O, SLAYMAKER O. 泥石流中巨石冲击力计算[M]. 泥石流观测与研究. 北京: 科学出版社, 1996: 67-72.

[11] WANG Quancai, CHEN Jian, WAO Hao, et al. Impact force of boulders conveyed in debris flows on bridge piers and anti-collision measures[J]. International Journal of Geohazards and Environment, 2016, 2 (2): 8-17.

[12] THORNTON C. Coefficient of restitution for collinear collisions of elastic perfectly plastic spheres[J]. Journal of Applied Mechanics, 1997, 64(2): 383-386.

[13] 何思明, 李新坡, 吴永. 考虑弹塑性变形的泥石流大块石冲击力计算[J]. 岩石力学与工程学报, 2007, 26(8): 1664-1669. HE Siming, LI Xinpo, WU Yong. Calculation of impact force of outrunner blocks in debris flow considering elastoplastic deformation[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26 (8): 1664-1669.

[14] BRACCESI C, LANDI L. A general elastic-plastic approach to impact analisys for stress state limit evaluation in ball screw bearings return system[J]. International Journal of Impact Engineering, 2007, 34(7): 1272-1285.

[15] YAMAGUCHI L. Erosion control engineering[M].Tokyo: Earth Press, 1985.

[16] MIZUYAMA T. Evaluation of impact of debris flow on check dams[J]. Journal of the Japan Society of Erosion Control Engineering, 1979, 32(3): 40-49.

[17] 赖绍文. 含砂水流之梳子坝撞击力试验分析[D]. 台湾: 台湾大学, 2005: 1-16.

[18]. 黄宏斌, 杨凯钧, 赖绍文. 土石流对梳子坝撞击力之研究[J]. 台湾水利, 2006, 55 (1): 41-58. HUANG Hongbin, YANG Kaijun, LAI Shaowen. Impact force of debris flow on filter dam[J]. Journal of Taiwan Water Conservancy, 2006, 55(1)：41-58.

[19] JOHNSON K L. Contact mechanics[J]. Journal of Tribology, 1985, 108(4): 464.

[20] RAOUS M, JEAN M, MOREAU J J. Contact mechanics[J].Springer Netherlands, 2009, 108(4): 464-468.

[21] 周必凡, 李德基, 罗德富, 等. 泥石流防治指南[M]. 北京: 科学出版社, 1991.

[22] THORNTON C, NING Zemin. A theoretical model for the stick/bounce behaviour of adhesive, elastic-plastic spheres[J]. Powder Technology, 1998, 99(2): 154-162.

[23] VU-QUOC L, LESBURG L, ZHANG Xiang. An accurate tangential force-displacement model for granular-flow simulations: contacting spheres with plastic deformation, force-driven formulation[J]. Journal of Computational Physics, 2004, 196(1): 298-326.

[24] ZHANG Xiang , VU-QUOC L. Modeling the dependence of the coefficient of restitution on the impact velocity in elasto-plastic collisions[J]. International Journal of Impact Engineering, 2002, 27(3): 317-341.

A study on the modified coefficient for impact force of bouldersconveyed in debris flow based on the Hertz theory

CHEN Jian1,2,3, WANG Quancai1,2, WANG Hao4, CHEN Yingqi1,2,3, LI Jun1,2,3

(1. Key Laboratory of Mountain Hazards and Surface Process, Chinese Academy of Sciences, Chengdu 610041, China;2. Institute of Mountain Hazards and Environment, Chinese Academy of Sciences, Chengdu 610041, China;3. University of Chinese Academy of Sciences, Beijing 100049, China;4. School of Civil Engineering and Architecture, Henan University, Kaifeng 475001, China)

Modified formula based on the Hertz elastic collision theory is one of the effective methods to calculate impact force exerted by boulders transported (IFEBT) in debris flow. However, there is no informative method to quantify the modified coefficient currently. A calculation model of IFEBT was built and the analytical equation of the modified coefficient was deduced based on the Hertz contact theory and the Thornton elastoplasticity hypothesis. The study shows that the modified coefficient is a function of material strength, boulder size, and velocity rather than constant. The IFEBT decreases with the growth of boulder velocity and increases with structure material strength and boulder size. The modified method was applied to control engineering for Ban Zigou debris flow. Calculation results show that the modified IFEBT in debris flow is only 15.58% of the one by the Hertz elastic theory. The modified coefficient is larger than 0.2 when boulder velocity is less than 3 m/s and ranges between 0.1 and 0.2 when boulder velocity is larger than 3 m/s.

debris flow; impact force of boulder; modified coefficient; Hertz contact mechanics; thornton elastoplasticity hypothesis

国家自然科学基金重点项目(41030742)；中国科学院专项研发与联合攻关服务(STS)项目(KFJ-EW-STS-094)

2016-04-27 修改稿收到日期： 2016-06-29

陈剑 男，博士生，1988年生

王全才 男，博士，研究员，1959年生

TU 45

A

10.13465/j.cnki.jvs.2017.16.004