水电站水机电-结构系统动力耦联模型研究及数值模拟

吴嵌嵌， 张雷克， 马震岳

(1.大连理工大学 建设工程学部水利工程学院，辽宁 大连 116023；2. 太原理工大学 水利科学与工程学院，太原 030024)

水电站水机电-结构系统动力耦联模型研究及数值模拟

吴嵌嵌1， 张雷克2， 马震岳1

(1.大连理工大学 建设工程学部水利工程学院，辽宁 大连 116023；2. 太原理工大学 水利科学与工程学院，太原 030024)

建立了包括引水系统、水轮机、调速器、发电机电磁系统、电网、水电机组轴系及厂房耦联结构等子模型在内全新的水电站系统非线性动力耦联模型。基于水力、电机、结构等学科理论构建了涉及水力、机械和电磁等因素的联立微分方程组，并采用有限元法建立机组轴系和厂房结构模型。结合Ansys的二次开发功能提出了水-机-电多因素影响下机组和厂房耦联结构模型不同工况动力特性的研究方法。采用差分法及特征线法等数值计算方法，利用该模型对水电站系统的开机工况进行了数值模拟计算和分析，同时对模型的合理性给予了验证。计算结果表明，该模型可以模拟计算水电站系统的开机工况运行过程，并能够较好反映水电站运行时的各种非线性动力特性。针对水电站系统较为复杂的特点，该模型的建立可对电站发电系统进行全面的数值模拟以评价和预测其运行安全性和结构可靠性，从而为水电站在极限工况和过渡工况的运行动态控制提供有益参考。

水电站系统；耦联模型；动力特性分析

水电站是电力系统的重要组成并承担着发电、调峰、调频和调相等任务，其运行稳定性和结构振动特性的研究是相关领域的主要内容之一。水电站运行是一个受不同系统相互影响的复杂动态过程，完整的水电站系统主要包括全流道、水轮机、调速器、发电机、机组轴系统及厂房结构等子系统。随着水电站装机容量的增大及水电站的快速发展(特别是抽水蓄能电站)，其结构巨型化和工况变化频繁化已成为必然的发展趋势，同时，水-机-电系统的稳定性、结构的振动特性及其相互之间的影响也会愈加突出，仅围绕各领域进行独立的研究而忽略彼此的影响关系已不能满足理论研究和工程实践的要求。显然，构建一种可以模拟分析电站运行过程中水力过渡过程、机械运动及其速度控制过程、电机暂态过程和结构振动特性的水电站系统模型，并利用该模型研究电站在极限工况和过渡工况时的运行稳定性，同时便于对机械和土建结构的动力特性进行分析，已变得迫在眉睫。

水电站各子系统的研究已开展多年且成果较为丰硕。压力管道研究对象则是流道中水流的水力过渡过程。Chaudhry[1-4]等推导了水锤控制方程，该方程也被称为一维过渡流方程，针对方程中的参数[5-7]及计算方法[8]也在相关文献中被提出并讨论。随着计算机技术的进步和发展，基于计算流体动力学(Computational Fluid Dynamics，CFD)求解的三维过渡流数值模型得以建立，该模型具有更高的计算精度和更为丰富的研究手段。Ruprecht等[9]则提出了一种由一维和三维建模相结合的数值模拟方法，该方法结合了一维模型和三维模型的优点，极大地提高了数值计算的效率和精度[10]。水轮机系统的研究对象是其运行过程中水头、流量、转速和导叶开度等因素非线性变化规律，过去也建立了线性及非线性的多种模型水轮机全特性曲线是一组概括了其全工况非线性特性的数据图，是针对水轮机运行模拟的重要工具，由于其离散性和高度非线性[11]，目前拟合法和插值法是利用其求解水轮机非线性过渡过程的主要方法。水轮机调速器模型的作用是调节水轮机过渡过程中的转速变化。Paynter等[12-13]建立了确定调节参数的基本准则。发电机系统的研究对象主要包括其运行过程中的电磁暂态和机电暂态过程。Kilgore等[14-15]创建了同步电机模型。随后，Heffron等[16]于1952年建立了Heffron-Phillips发电机模型并用于电力系统稳定性分析。除上述子系统外，水电站系统还包括水轮发电机组轴系统和厂房结构系统。水电机组通常被简化为转子-轴承系统模型，轴承模型的核心则是对于轴承油膜力动态特性的准确描述。此外，旋转结构的非线性动力响应特性是转子-轴承系统的另一个重要研究内容[17-18]。然而，上述针对转子-轴承系统的研究在模型中大多采用固定端约束来处理轴承的边界条件，而实际中机墩及厂房则表现为一种弹性结构。显然，传统的处理方式无法准确表述机组和厂房结构之间的相互影响。而传统的厂房结构研究，也均未将机组结构纳入整体模型之内，对于两者之间的耦联特性研究更是鲜有提及[19-20]。其研究方向则主要集中在两个方面：①厂房结构优化及荷载传递路径研究[21-22]；②结构自振特性和动力响应特性研究[23]。

但是从上述研究中可以看出，尽管国内外学者在机组及厂房结构振动领域进行了大量的卓有成效的探索，同时针对水-机耦合，机-电耦合或水-机-电三者耦联过渡过程[24-25]也开展了相当的工作并取得了一定成果，然而，这些研究均没有考虑结构振动和耦联过渡过程两者之间的联系。一方面，结构振动分析针对水电站机组的研究过于孤立，对实际运行工况变化的影响考虑甚少；另一方面，耦联过渡过程研究只是讨论了电站运行过程中各系统的稳定性问题而没有将其对结构振动的影响纳入研究范围。可以说两者均有一定的偏向性，其优点是能够针对具体对象进行细致、透彻的研究，缺点则是没有建立起系统的整体模型从而无法形成完整的分析体系。

鉴于此，本文利用各子系统中关键参数之间的联系建立了一种全新的水电站系统模型。该模型包括压力管道一维过渡流模型、水轮机非线性模型、PID调速器模型、同步电机三阶模型、机组轴系和厂房耦联结构模型，以及可倾瓦导轴承模型等子模型。以某实际水电站的开机工况为算例进行了分析验证，计算结果表明，本文所提出模型一方面可用于研究水电站运行过程中极限工况和瞬态工况中的系统稳定性调节特性，另一方面可以分析结构动力荷载输入所需要的水力、机械和电磁等参数，并对荷载进行深入模拟，进而分析不同工况多因素影响下耦联结构的动力特性。利用该模型能够更加全面地描述水电站的运行特性，从而为系统稳定运行和结构安全预测控制提供可靠保证。

1 数值模型

在一个完整水电站系统中，机组及厂房耦联结构是其中的核心组成部分，机组实现能量转换过程，厂房为机组提供可靠支承。耦联结构维系着水力、机械、电磁等不同子系统之间的联系，即压力管道引导水流至厂房并经过蜗壳流道将势能转化为动能(水轮机功率)，推动水轮机发电机组轴系的转动，在旋转过程中电机的线圈切割由励磁系统产生的强磁场而感应出电能，输出的电能(电磁功率)依据电网负荷要求而波动，两种功率产生两种方向相反的力矩作用在水轮发电机组轴系上，并由调节系统控制两种功率的变化以达到让机组平稳运行的目的。同时，结构系统承担着运行过程中由水力脉动、机组旋转、励磁电流等因素形成的荷载而产生振动，该振动反过来会影响机组运行和相关荷载变化，从而使整个系统处于一种动态耦联的状态。水力发电系统的组成如图1所示。

图1 水力发电系统组织框架图Fig.1 Sketch of hydroelectric station system

为了更好地说明整体数学模型，将系统分为5个子模块，并在1.1节～1.5节对建立的非线性动力学模型予以介绍。

1.1 压力管道模型

Chaudhry等提出的一维压力管道模型具有物理意义明确，计算简便等优点，而三维模型可提供更高的计算精度并包含更丰富的分析内容。由于本文主要用以求解水电站引水系统的流量Q和水头H，忽略了流体的运动对管道结构的影响，相比于更加复杂的三维模型而言，一维模型在压力管道过渡流的分析中既能满足计算精度也能提高计算效率。故本文选取一维压力管道模型模拟水电站压力管道过渡流。如图2所示，压力管道是连接水轮机和水库的流道，其一维过渡流动量方程和连续方程可表示为

(1)

(2)

式中：D、A分别为压力管道直径、截面积；H和Q分别为压力管道水头和流量。

图2 流道及边界条件Fig.2 Boundary conditions

利用有限差分(Fininte Difference Method，FDM)原理并使用式(3)和式(4)对上述方程进行网格划分并离散化

(3)

(4)

式中，下标i和n分别为位置点i和时间点n。

在此基础上，利用特征线方法(MethodofCharacteristics，MOC)推导边界方程与上述方程组成含有2n个未知数的方程组。水轮机代表压力管道的下游边界，在时间点n处其对应的正特征方程为

Qp=A(Cp-CaHp)

(5)

式中，Ca=g/a，a为水锤波速。

(6)

同时，水库作为压力管道上游边界条件，在时间点n处其对应的负特征方程为

(7)

(8)

式中：下标1，2为在各时间点处上游边界两个位置节点；下标L，M分别为在时间点n处下游边界两个位置节点；下标P为时间点n+1处下游边界末端的位置节点。如上游边界条件(H1,Q1)和下游边界条件(Hp,Qp)已知，联立求解式(3)～式(8)便可得压力管道内各个节点处的流速(流量)和水压力(水头)。其中：H1为上游水库的水头；Qp为水轮机的工作流量。

1.2 水轮机模型

水轮机将水能转化为机械能，其旋转运动方程为

(9)

式中：J为机组转动惯性矩；ωm为机械转速；θm为机械转角；Mt、Me分别为机械转矩，电磁转矩。转速ω、水轮力矩Mt、流量Q和开度τ共同决定了水轮机的工作状态。参考文献[26]在大量假设的基础上建立了水轮机线性模型。此后，Vournas等[27-28]考虑了弹性压力管道和可压缩性水体的影响并对模型进行了改进，这些模型均对上述各变量之间的关系进行了简化。其优点是对于适用于理论分析，但是实际运行的水轮机来说，不能充分的体现其高度非线性。针对该情况，本文采用由实验数据整理而来的综合特性曲线可较好地呈现这4个变量的非线性关系，即

(10)

由于该曲线具有高度非线性特性，无法建立具有明确物理意义的数学表达式，为了应用曲线上的数据，需将曲线的离散数据输入计算机，然后利用拟合和插值方法求得水轮机全工况的运行参数。当前一时间步长的流量、转速和导叶开度已知时，参数Hnp和Pt(Mt)可利用迭代法求出。如图2所示，Hp与Hnp、Qp的关系由式(11)表示

(11)

式中，Hnp为水轮机工作净水头。

联立求解式(11)和式(5)可得Hp和Qp，其中下标p为所求时间步上的管道下游边界点。该时间步长下的导叶开度可由调速器模型求得，而此时的转速则需要获得同步电机模型中的电磁功率Pe后才能够得到。

1.3 调速器模型

PID(ProportionIntegrationDifferentiation)是水轮机调节中经典的调节规律，主要包含比例调节、积分调节和微分调节等，其存在保证了调速器的稳定性、快速性和准确性[29]。在此基础上，相关研究或对PID调节规律进行了改进[30-31]或进一步提出了新的调节规律[32-33]，均取得了良好的效果。故本文采用该调速器模型模拟水轮机转速随电力系统负荷变化而改变的情况。如图3所示，Cf作为频率给定值，x～y的传递函数可表示为

(12)

式中：KD=Tn/bt；KP=1/bt；KI=1/(btTd)；KP、KI、KD分别为比例增益、积分增益、微分增益；bp为永态转差系数；bt为暂态转差系数；Td为缓冲时间常数；Tn为加速时间常数；Ty为主接力器反应时间常数；x为转速偏差输入值；y为接力器行程输出值。利用反拉普拉斯变换可以得到一个三阶微分方程

图3 水力发电系统组织框架图Fig.3 The transfer function of the frequency regulation mode

bpKDTyy‴+(bpKPTy+bpKD)y″+(bpKITy+bpKP+1)y′+

bpKIy=KDx″+KPx′+KIx

(13)

根据现代控制理论，由式(13)推导出状态方程，可得一组一阶微分方程组

(14)

式中:β0=b0，β1=b1-a1β0，β2=b2-a1β1-a2β0，β3=

b3-a1β2-a2β1-a3β0；a1=(bpKPTy+Ty+bpKD)/bpKDTy， a2=(bpKITy+bpKP+1)/bpKDTy，a3=bpKI/bpKDTy； b0=0， b1=KD/bpKDTy，b2=KP/bpKDTy，b3=KI/bpKDTy。

利用四阶Runge-Kutta法可以求解方程中的x1，再由式 y=x1+βx求得接力器行程，进一步得到导叶开度值，y为水轮机接力器行程。

1.4 同步电机及电网模型

同步电机模型描述了电机内部参数之间的关系。常见的同步电机模型包括三阶模型[34]和五阶模型[35]等。为了简化模型即忽略了电机中的次暂态过程，本文采用了前者，在以后的分析中如果需要也同样可以采用其他阶数的同步电机模型。在该模型中可以求得电磁功率Pe，端电压UG和电流I。凸极同步电机向量图如图4所示：E′为暂态电动势；φ为发电机功率因数角；ψ为发电机内功率因数角。图中发电机端电压和定子电流的关系为

(15)

式中：I、Id、Iq分别为定子电流及其分量；Pe为电磁功率；UG、UGd、UGq为端电压及其分量；Xq为q轴同步电抗。

图4 同步凸极电机相量图Fig.4 Phasor diagram of synchronous generator

同时，发电机的输出功率由输电线路输入电网，供给电网中的负荷消耗。为了考虑电网的影响，此模型中利用电网负荷随电压变化的特性，并采用恒定阻抗模型来表示负荷，则端电压和负荷电压的关系可表示为

(16)

式中：Re、RL分别为输电线、负荷功率电阻；UL为负荷电压；Xe、XL分别为输电线路及负荷功率电抗。

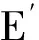
(17)

需要指出的是，由于不考虑电机的次暂态过程，本文在推导式(15)的过程中忽略了转子阻尼绕组和定子电阻的影响即次暂态的变化过程。

(18)

发电机的自动励磁调节系统采用按电压偏差值调节方式，其方程为

(19)

式中：Te为励磁机时间常数；Kv为调节器综合放大系数。

根据公式ωe=pnωm和P=Mωm(pn为磁极对数；ωe为电磁转速)将转子运动方程中的机械角速度和转矩转化为对应的电角速度和功率，则式(9)中转子运动方程及功角变化方程可用标幺值表示为

(20)

1.5 耦联结构模型

由于厂房结构具有体积大和结构复杂等特点，该模型的建立通常采用有限元方法。需要指出的是，厂房模型在本文中仅作为一种弹性支撑结构出现，因为在稳定的开机过程中其结构振动响应较小，算例中没有对其进行分析。在转子-轴承系统中，转子系统的模型包含集总参数参数模型和有限元模型等。而轴承模型则可分为长、短轴承[36]和有限元等类型[37]。一般而言，在一定的假设前提下前两个非线性模型能够得到解析解[38]，而有限元模型只能计算出数值解。由于厂房结构模型采用了有限元方法建立，为了与之契合，转子系统模型和轴承系统也采用了有限元法构建。

如图5(a)所示，典型的地面厂房结构模型包含上部排架各层楼板、风罩、机墩、蜗壳及尾水管混凝土等结构，厂房模型底部为固定端约束，其他为自由端，不同工况下水压脉动可以施加在厂房结构上。水轮发电机组轴系统通常简化为转子-轴承系统。本文采用有限元方法建模，利用梁单元模拟机组主轴，质量单元模拟转子和转轮，弹簧单元模拟导轴承，一个典型轴系统的模型如图5(b)所示。导轴承的动力特性采用弹簧单元的刚度和阻尼系数(kij,cij)表示，机组整体模型可利用约束方程和厂房结构耦联起来。

图5 厂房结构模型及机组轴系简化模型示意图Fig.5 Structural model

用可倾瓦导轴承模型如图6所示。当大轴转速较低时，轴承内瓦块四周的径向油膜压力场可以用雷诺方程表示为

(21)

式中：h为导轴承油膜厚度；p为导轴承油膜压力，其方程的无量纲形式为

(22)

图6中：Ri、Ro分别为轴瓦内径和外径；αp为导轴承轴瓦张角；β为导轴承轴瓦支撑点方位角；δp为导轴承轴瓦偏位角；ηl为导轴承轴瓦方位角；θb为导轴承轴承偏位角。

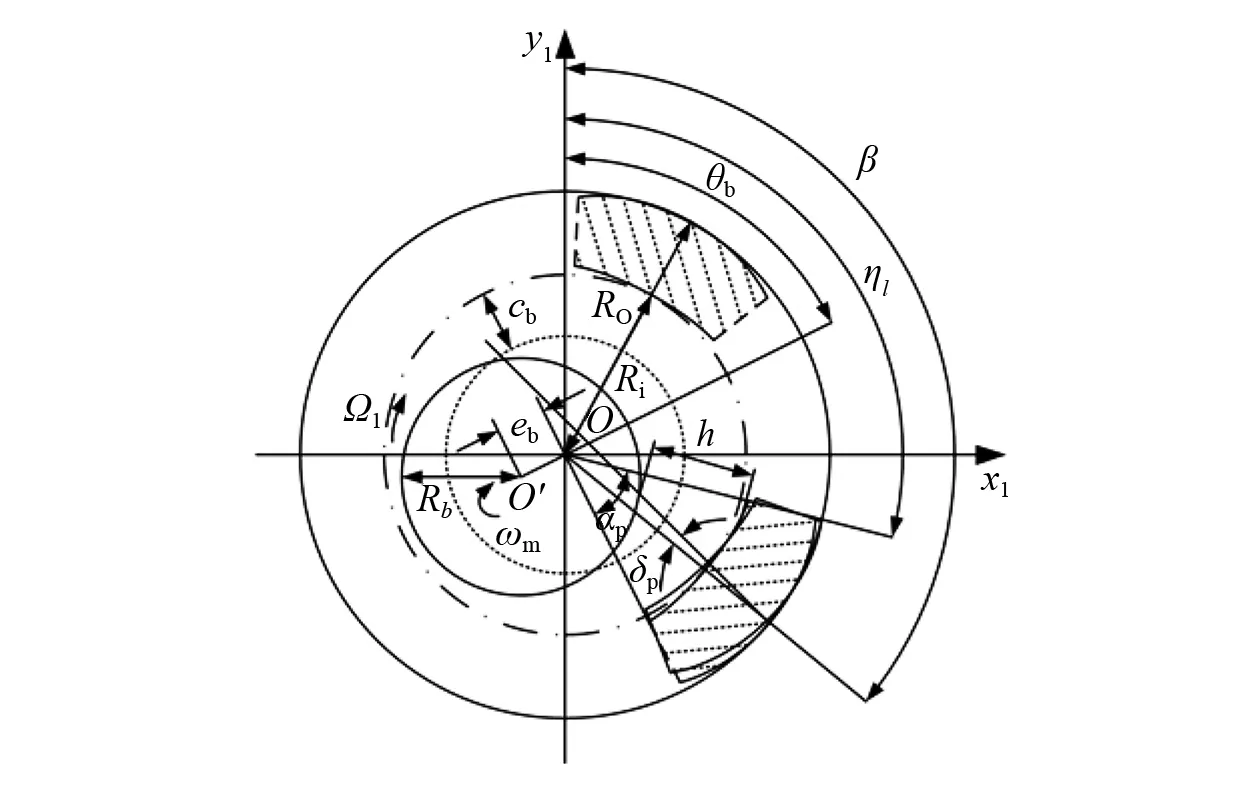
图6 可倾瓦导轴承示意图Fig.6 Tilting pad guide bearing

而x1=Rηl，λ=y1/(Lb/2)，λ∈[-1,+1]，Lb为导轴承轴瓦长度，λ为导轴承轴瓦沿大轴轴向的无量纲坐标。无量纲的油膜厚度参数为

δp/bsin(β-ηl)

(23)

式中：ε=eb/cb为轴承偏心；b=cb/Rb为间隙比，Rb为轴颈半径，cb、eb分别为轴颈间隙和偏心。动态雷诺方程如式(24)，其中u和v分别为油膜的周向速度和径向速度。

(24)

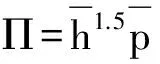
(25)

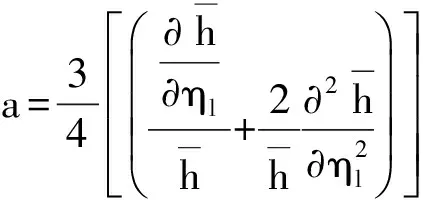
利用有限元法可计算得到油膜压力，然后利用单元积分求出油膜力。油膜力f对x1、y1方向位移和速度的偏导数分别为

(26)

式中：K、C分别为刚度、阻尼系数；下标i、s分别为x1、y1。在求出每块瓦的刚度和阻尼系数后，轴系整体的刚度和阻尼系数通过各瓦块组合便可获得。

2 水力发电系统模拟及计算流程

本文选用型号为“HL180-LJ-410”的水轮机作为研究对象。受篇幅所限，选取较为简单的开机过程作为模拟对象，开机的数值模拟过程共历时43s，并在水轮机转速、出力和流量等稳定后于第27s开始发电机的建压过程。机组开机过程中发电机处于空载状态，不涉及电机的电磁暂态过程，但考虑发电机建压过程中产生的励磁电流，即计算中考虑作用在转子系统上的机械偏心力和不平衡磁拉力[39]。水轮机、调速器、发电机和转子-轴承模型数据见表1，厂房结构模型依据某实际水电站厂房建立。其中：er、cr分别为定转子空气间隙、转子偏心；Ra为机组大轴半径；Rr和Lr分别为转子半径和转子长度；Tw为水流时间常数；If为励磁电流，Tm为机组惯性时间常数。

基于第1节各子模型的介绍，水电站系统的求解过程如图7所示。该模型中的结构部分由Ansys建立，其他部分由Fortran语言编写。然后利用Ansys中的UserProgrammableFeatures(UPFs)功能将Fortran程序编译成为用户可以随时调用的外部命令。这样在动力时程分析时就能在每个时步中计算水机电耦联的过渡过程，对水轮发电机组的运行过程进行模拟，从而对水电站结构耦联模型在任何工况下进行动力特性分析。

3 数值模拟和结果分析

图8反映了该水轮机从开机到空载过程中转速、开度和水轮机功率的变化情况。从图8中可以看出，在开机阶段，机组转速上升平稳，几乎没有超调现象出现。导叶开度首先在短时间内达到启动开度，随着转速升至额定值其开度开始产生波动，并最后稳定在空载开度。同时，水轮机输出功率在开始阶段也快速增加使水轮机的驱动力矩不断增大从而为转速的升高提供动力，当转速趋于稳定时，输出功率在经历短暂的波动后也减小为0。图8中所述变化规律与文献[40]介绍的开机规律有较好的吻合。

表1 模型参数表

图7 系统分析计算流程图Fig.7 Computational process of system

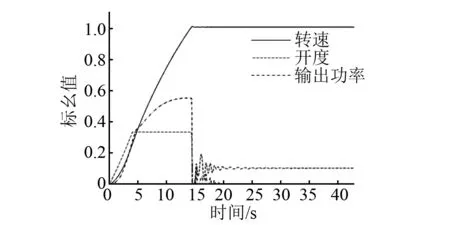
图8 开机过程瞬态变化Fig.8 Simulation result of starting-up transient

图9表示水轮机工作流量和水头在开机至空载阶段的变化规律。从图9(a)中可以发现，水轮机流量在开始时增速较快，这是由于导叶开度的快速增大所引起的。当导叶开度稳定在开机开度时，流量开始缓慢减小。在开机第15 s附近，由于水轮机转速达到额定转速，此时调速器为了防止出现转速超调情况，将调整导叶开度以减小水轮机输出功率，在这个过程中开度迅速降至0，进而水轮机流量也相应变为0。随后，因为导叶开度出现波动，流量也随之产生波动，当开机时间达到第22 s时流量则趋于稳定。同样，随着导叶突然开启使得开度增加，水轮机工作水头出现了先下降再回升的过程，如图9(b)所示。在第15 s时，由于导叶开度突降导致工作水头激增达到峰值(此时会在压力管道中产生较大的水压力)，此后随着导叶开度的波动逐步趋向稳定，水头也相应发生变化并最终达到稳态。流量和水头的变化遵从了在实际开机过程中先较大幅度变化，随后小幅度波动，最终趋于稳定的规律。

(a) 水轮机流量变化

(b) 水轮机工作水头变化

图10和图11分别为机组在开机过程中转子、转轮和导轴承轴心总体位移图和轨迹图。以图10所示作为基础，结合图11的轴心轨迹以及图8的转速变化可知，在转速达到额定值之前，转子、转轮和导轴承轴心总位移是随着转速增加而逐渐增大的，当转速等于额定值时其轴心位移均达到稳定值。从图10(a)可以看出，由于转子的重量较大，其所受偏心力大于转轮，所以相应地转子的轨迹运动幅值比转轮大；图10(b)中所呈现的导轴承轴心轨迹运动规律则与图10(a)类似，各导轴承稳态轨迹振幅按大小排列依次为下导、水导和上导，这也反映了每个导轴承受转子、转轮振动的影响程度，即距离转子和转轮较近的下导和水导轴承会因承受较大的作用力而产生较大的位移。

(a) 旋转体总位移图

(b) 导轴承轴心总位移图图10 时程-水平总位移图Fig.10 The total axis displacement in horizontal direction

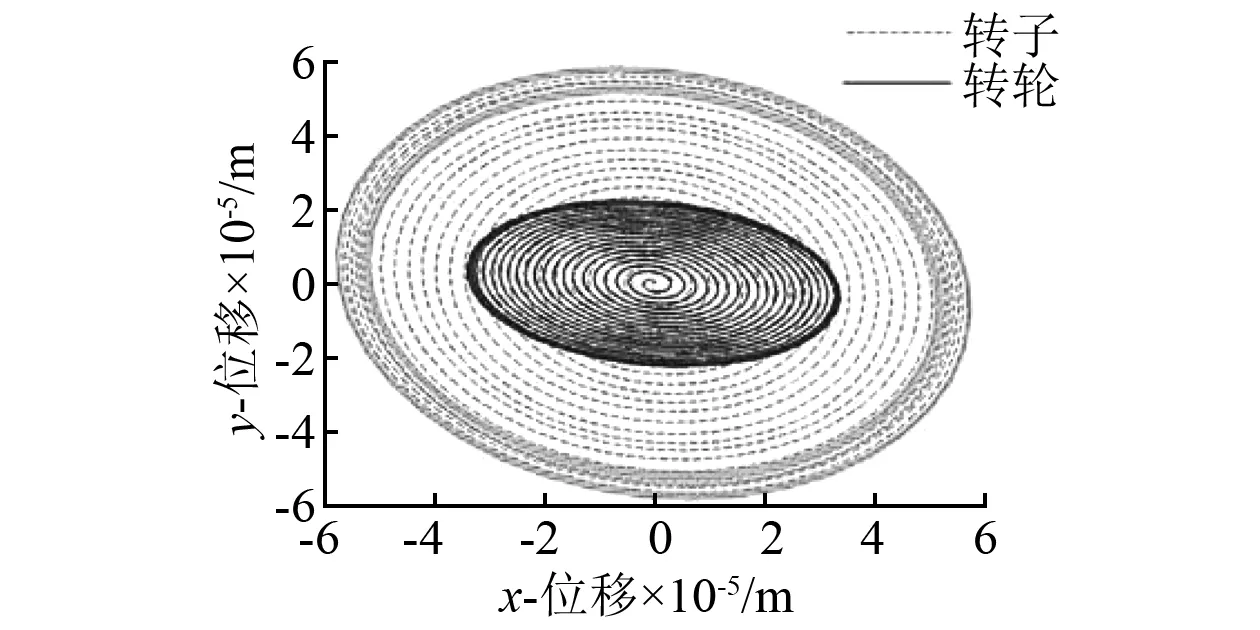
(a) 旋转体轴心轨迹图

(b) 导轴承轴心轨迹图图11 水轮机工作流量和水头变化Fig.11 The axis trajectories in horizontal ddirection

本文设定发电机的建压过程始于开机后27 s，此时励磁电流同步产生并逐渐增加，相应地不平衡磁拉力(Unbalanced Magnetic Pull，UMP)出现并随着励磁电流的上升而逐渐增大，其随时间的变化规律如图12所示。在UMP的作用下，结合图10和图11观察可知从第27 s开始，转子的轴心轨迹振幅开始变大，同时下导和上导的轴心运动幅值也有不同程度的增加。从图12中可以发现，在第32 s时UMP进入稳定阶段但是处于动态平衡状态。一方面，这是因为端电压达到额定值时，励磁电流处于稳定状态从而UMP也趋于稳定；另一方面，因为UMP的大小和转子的轴心位移有关，所以受此影响其又会产生一定程度的波动，相应的图10和图11中转子和下导轴心轨迹也随UMP的变化达到一个新的动态稳定阶段。

图12 建压过程UMP变化图Fig.12 The change of UMP during starting-up process

结合图9和图10可知，在第27 s建压开始之前，当转子的轴心总位移历经增大和稳定两个阶段时，流量和水头并没有产生相应的变化而是随开度的增减相应发生波动。当建压开始后，转子的轴心总位移随UMP的增大而增大，在此过程中水轮机的工作流量和水头依旧因开度不变而保持稳定或趋于稳定，这说明开机阶段转子的振动不会对水轮机的水力过渡过程产生影响。

4 结 论

基于水力、机电和结构等学科理论基础，本文构建了水电站水机电-结构系统的耦联模型。利用Ansys的UPFs功能，在结构动力时程计算的时步中实现了针对本时步的水机电耦联过渡过程的计算，相关结论如下：

(1)在整体模型的基础上结合多种数值计算方法模拟了某实际水电站开机过程中各参数的变化规律，并与以往研究进行对比分析，相关结果呈现了较好的吻合性，验证了所提出模型的合理性。

(2)通过数值计算方法成功模拟了机组在开机过程中所受偏心力和UMP的变化规律，同时，机组在上述两种激励共同作用下的机组轴系动力特性也得到了很好的体现，验证了所提出模型的有效性。

需要说明的是，水电站运行包括开机、增减负荷和甩负荷等诸多工况，受篇幅所限，本文仅针对开机工况进行了分析。此外，由于开机阶段水轮机水压脉动很小且发电机处于空载状态，因此本文在分析过程中未将压力脉动和电机暂态过程纳入考虑范围之内。然而，水力荷载和电磁荷载同属水电站系统运行过程中的重要激励源，其存在必然会对电站各工况带来不同的影响。在未来的研究工作中，作者将对水电站系统的其他运行工况予以考虑并着重讨论上述激励源对系统的影响，同时建立起压力脉动和结构动力特性之间的动态耦联关系，从而完善模型用以研究多种工况下水电站系统各子模块之间的相互联系和动力特性，为水电站的安全稳定运行提供更为坚实的理论支撑。

[ 1 ] CHAUDRY M H. Applied hydraulic transients [M]. New York: Van Nostrand Reinhold Company, 1979.

[ 2 ] COLLATZ L. The numerical treatment of differential equation [M]. 3 ed. Berlin: Springer, 1960.

[ 3 ] WYLIE E B, STREETER V L, SUO L S. Fluid transient in systems [M]. Englewood： Prentice-Hall， 1993.

[ 4 ] GHIDAOUI M S. On the fundamental equations of water hammer [J]. Urban Water Journal, 2004(2): 71-83.

[ 5 ] PARMAKIAN J. Water-hammer analysis[M]. Englewood: Prentice-Hall, 1955.

[ 6 ] 杨建设.瞬变流动中水力摩损的影响研究[J]. 水利学报，1999(2)：67-70. YANG Jianshe. Study on the influence of hydraulic friction to transient flow[J]. Journal of Hydraulic Engineering, 1999(2): 67-70.

[ 7 ] 江春波，焦云乔，李丹.有压管道的非恒定摩阻模型[J].清华大学学报(自然科学版), 2009, 49(3):347-351. JIANG Chunbo, JIAO Yunqiao, LI Dan. Transient friction models in pressurized pipes[J]. Journal of Tsinghua University (Natural Science), 2009, 49(3):347-351.

[ 8 ] YANG J C, HSU E L. On the use of the reach-back characteristics method of calculation of dispersion[J]. International Journal for Numerical Methods in Fluids, 1991, 12(3): 225-235.

[ 9 ] RUPRECHT A, HELMRICH T. Simulation of the water hammer in a hydropower plant caused by draft tube surge[C]∥4th ASME/JSME Joint Fluids Engineering Conference. Honolulu: ASME, 2003.

[10] ZHANG X X, CHENG Y G, YANG J D, et al. Simulation of the load rejection transient process of a Francis turbine by using a 1D-3D coupling approach[J].Journal of Hydrodynamics, 2014, 26(5):715-724.

[11] 王宜怀，沈祖诒，孙涌.基于主曲线方法的水轮机特性曲线的数值拟合[J].水力发电学报, 2009, 28(3):181-186. WANG Yihuai, SHEN Zuyi, SUN Yong. Numerical simulation of characteristic curves of hydraulic turbine based on principal curves[J].Journal of Hydroelectric Engineering, 2009, 28(3):181-186.

[12] PAYNTER H M. A palimpsest on the electronic analog art[M]. Boston: George A. Philbrick Researches, Inc., 1955.

[13] HOVEY L M. Optimum adjustment of hydro governors on Manitoba hydro system[J]. Power Apparatus and Systems Part III Transactions of AIEE, 1962, 81(3): 581-587.

[14] KILGORE L A. Calculation of synchronous machine constants[C]∥ AIEE Transactions. Asheville: IEEE, 1931, 50: 1201-1214.

[15] WRIGHT S H. Determination of synchronous machine constants by test[C]∥ AIEE Transactions. Asheville: IEEE, 1931, 50: 1331-1351.

[16] HEFFRON W G, PHILLIPS R A. Effect of a modern amplidyne voltage regulator on underexcited operation of large turbine generators[J]. IEEE Transactions on Power Apparatus and Systems, 1952, 71(1): 692-697.

[17] ZHANG L K, MA Z Y, SONG B W. Dynamic characteristics of a rub-impact rotor-bearing system for hydraulic generating set under unbalanced magnetic pull[J].Archive of Applied Mechanics, 2013, 83(6): 817-830.

[18] WU Q Q, ZHANG L K, MA Z Y. Numerical simulation and nonlinear stability analysis of Francis hydraulic turbine-seal system[J]. Jordan Journal of Mechanical and Industrial Engineering, 2015, 9(4): 253-261.

[19] 宋志强.水电站机组及厂房结构耦合振动特性研究[D]. 大连：大连理工大学, 2009.

[20] 孙万泉，黄雄辉.水电站机组与厂房结构耦合动力系统振动路径识别[J].振动与冲击, 2014, 33(6):23-28. SUN Wanquan, HUANG Xionghui. Identification of vibration transfer path for the coupled system of water turbine generator set and power house[J].Journal of Vibration and Shock, 2014, 33(6):23-28.

[21] 欧阳金惠，陈厚群，张超然.大型水电站蜗壳埋设方式对厂房振动的影响分析[J].水力发电学报, 2012, 31(4):162-166. OUYANG Jinhui, CHEN Houqun, ZHANG Chaoran. Analysis on powerhouse vibrations with spiral cases in different embedding manners for large-scale hydropower station[J].Journal of Hydroelectric Engineering, 2012, 31(4):162-166.

[22] 徐伟，马震岳，职保平.水压脉动能量传导对水电站厂房墙体影响分析[J].水力发电学报, 2013, 32(2):233-238. XU Wei, MA Zhenyue, ZHI Baoping. Analysis on power flow transmission of pressure fluctuation along the walls of hydropower house[J].Journal of Hydroelectric Engineering, 2013, 32(2):233-238.

[23] 张存慧，马震岳，周述达，等.大型水电站厂房结构流固耦合分析[J].水力发电学报, 2012, 31(6):192-197. ZHANG Cunhui, MA Zhenyue, ZHOU Shuda, et al. Analysis of fluid-solid interaction vibration characteristics of large-scale hydropower house[J].Journal of Hydroelectric Engineering, 2012, 31(6):192-197.

[24] 赵桂连.水电站水机电联合过渡过程研究[D]. 武汉：武汉大学，2004.

[25] 周昆雄，张立翔，曾云.机-电耦联条件下水力发电系统暂态分析[J].水利学报, 2015, 46(9):1118-1126. ZHOU Kunxiong, ZHANG Lixiang, ZENG Yun. Transient modeling of hydraulic electricity-generating system in water-machine-electricity coupling conditions[J].Journal of Hydraulic Engineering, 2015, 46(9):1118-1126.

[26] IEEE Committee. Dynamic models for steam and hydro turbines in power system studies[J]. IEEE Transactions on Power Apparatus and Systems, 1973, 92(6): 1904-1915.

[27] VOURNAS C D. Second order hydraulic turbine models for multimachine stability studies[J]. IEEE Transactions on Energy Conversion, 1990, 5(2): 239-244.

[28] MAHMOUD M, DUTTON K, DENMAN M. Dynamic modeling and simulation of a cascaded reservoirs hydropower plant[J]. Electric Power Systems Research, 2004, 70(2): 129-139.

[29] 魏守平，卢本捷.水轮机调速器的PID调节规律[J]. 水力发电学报，2003(4)：112-118. WEI Shouping, LU Benjie. On the PID regulating rule of hydro turbine governor[J]. Journal of Hydroelectric Engineering, 2003(4): 112-118.

[30] 周建中，赵峰，李超顺.基于的水轮机调速系统非线性控制参数优化方法研究[J].水电能源科学, 2014, 32(12):127-130. ZHOU Jianzhong, ZHAO Feng, LI Chaoshun. Nonlinear PID parameters optimization for hydraulic turbine governing system based on GSA[J]. Water Resources and Power, 2014, 32(12): 127-130.

[31] ANWAR M N, PAN S. A new PID load frequency controller design method in frequency domain through direct synthesis approach[J]. Electrical Power and Energy Systems, 2015, 67(4): 560-569.

[32] 李超顺，周建中，安学利，等.基于-模糊模型的水轮机调节系统辨识[J].武汉大学学报, 2010, 43(1):108-111. LI Chaoshun, ZHOU Jianzhong, AN Xueli, et al. Identification of hydro-turbine governing system based on T-S fuzzy model[J]. Engineering Journal of Wuhan University, 2010, 43(1): 108-111.

[33] 寇攀高，周建中，张孝远，等.基于滑模变结构控制的水轮机调节系统[J].电网技术, 2012, 36(8):157-162. KOU Pan’gao, ZHOU Jianzhong, ZHANG Xiaoyuan. An improved hydro-turbine governing system model and design of sliding mode variable structure controller[J].Power System Technology, 2012, 36(8):157-162.

[34] 田立军，陆于平，陈珩.抽水蓄能电机调相运行时的动态稳定性能分析[J].电网技术, 1998, 22(4):10-12. TIAN Lijun, LU Yuping, CHEN Heng. Dynamic stability analysis for pumped storage machines under synchronous condenser operation conditions[J].Power System Technology, 1998, 22(4):10-12.

[35] SAYIDI A M, NEKOUI M A, BOGHRABIDI N S. Adaptive optimal control for a one-machine infinite-bus power system[C]∥ Computational Intelligence for Modelling Control and Automation.[S.l.]:IEEE, 2008:202-207.

[36] 闻邦椿，顾家柳，夏松波，等.高等转子动力学-理论、技术与应用[M]. 北京：机械工业出版社，2000.

[37] 马震岳，董毓新.水电机组可倾瓦导轴承动力特性系数[J].动力工程, 1990, 10(6):6-11. MA Zhenyue, DONG Yuxin. Dynamic coefficients of tilting pad guide bearings of hydraulic turbine sets[J].Power Engineering, 1990, 10(6):6-11.

[38] ADILETTA G, GUIDO A R, ROSSI C. Nonlinear dynamics of a rigid unbalanced rotor in journal bearings. Part I: theoretical analysis[J]. Nonlinear Dynamics, 1997, 14(1): 57-87.

[39] GUO D, CHU F, CHEN D. The unbalanced magnetic pull and its effects on vibration in a three-phase generator with eccentric rotor[J].Journal of Sound and Vibration, 2002, 254(2):297-312.

[40] BAO H Y, YANG J D, FU L. Study on nonlinear dynamical model and control strategy of transient process in hydropower station with Francis turbine[C]∥ Asia-pacific Power and Energy Engineering Conference.[S.l.]:IEEE, 2009: 1-6.

Model analysis and numerical simulation of a dynamic coupledhydraulic-mechanical-electric-structural system for a hydropower station

WU Qianqian1, ZHANG Leike2, MA Zhenyue1

(1. School of Hydraulic Engineering, Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian 116023, China; 2. College of Water Resources Science and Engineering, Taiyuan University of Technology, Taiyuan 030024, China)

A novel nonlinear dynamic coupled model for a hydropower station system, which contains the model of a water-carriage system, a water turbine system, a speed governor system, a generator's electromagnetic system as well as grid, a structural system with shaft of hydroelectric generating unit and powerhouse, was established. Firstly, the simultaneous differential equations for coupled hydraulic-mechanical-electric transient process were set up based upon the theories of hydraulics, electric machinery, etc., while the coupled structural models of shaft for unit and powerhouse were built by means of the finite element method. Secondly, a new method for investigating nonlinear dynamic properties of structures, which was influenced by coupled hydraulic-mechanical-electric factors in different conditions, was introduced with the help of user programmable features of Ansys software. Finally, in order to verify the rationality, several numerical calculation methods were used to simulate and study the start-up process. The results indicate that the model presented in this paper can be adopted to simulate the start-up condition and reflect the nonlinear dynamic characteristics of hydroelectric station comprehensively. It is meaningful to supply an overall numerical result with assessing the operation safety and structures reliability. Furthermore, some references for dynamic regulation during limited and transient conditions of hydroelectric station can also be provided.

hydroelectric system; coupled model; dynamic simulation

国家自然科学基金(51379030)；太原理工大学校青年基金(2015QN029)

2016-01-26 修改稿收到日期： 2016-06-17

吴嵌嵌 男，博士生，1985年生

马震岳 男，博士，教授，1962年生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.16.001